Справочник по планиметрии. (7-9 класс) презентация

Содержание

Использованные ресурсы. 1.Л.С. Атанасян, В.Ф. Бутузов и др. Геометрия, 7-9. М. :Просвещение, 2008. 2. Л.И. Звавич, А.Р. Рязановский Геометрия в таблицах, 7-11кл. : Справочное пособие/М. :Дрофа, 2002.

Слайд 1ОСНОВНЫЕ ФАКТЫ КУРСА ПЛАНИМЕТРИИ.
7-9 КЛАСС.
СОЗДАТЕЛЬ ПРЕЗЕНТАЦИИ УЧИТЕЛЬ МАТЕМАТИКИ АНКИНА Т.С.
Г. ЕКАТЕРИНБУРГ

МАОУ-ГИМНАЗИЯ №13

Справочник планиметрии.

Слайд 2Использованные ресурсы.
1.Л.С. Атанасян, В.Ф. Бутузов и др. Геометрия, 7-9. М. :Просвещение,

2008.

2. Л.И. Звавич, А.Р. Рязановский
Геометрия в таблицах, 7-11кл. :
Справочное пособие/М. :Дрофа, 2002.

Слайд 3Как пользоваться справочником.
После прочтения инструкции перейдите на следующий слайд «Основные темы».
Выбрав

тему, «кликните» по её названию.
Для продолжения просмотра выбранной темы «кликните» по стрелке «Далее».
Для возвращения к списку тем «кликните» по кнопке «Вернуться»

Слайд 4Основные темы.
1.Углы и параллельность.
2.Треугольник.
3.Параллелограммы.
4. Трапеции.
5. Окружность.
7. Правильные многоугольники.
6. Площади.
Закрыть справочник.

Слайд 5Углы и параллельные прямые.
1.Углы и их виды.
2.Углы и параллельные прямые.
4.Теорема Фалеса.
3.

Аксиома параллельных. Свойства.

Вернуться

Слайд 6сторона
В
А
С
вершина



биссектриса
ВАС

АМ - биссектриса
ВАМ= САМ



М
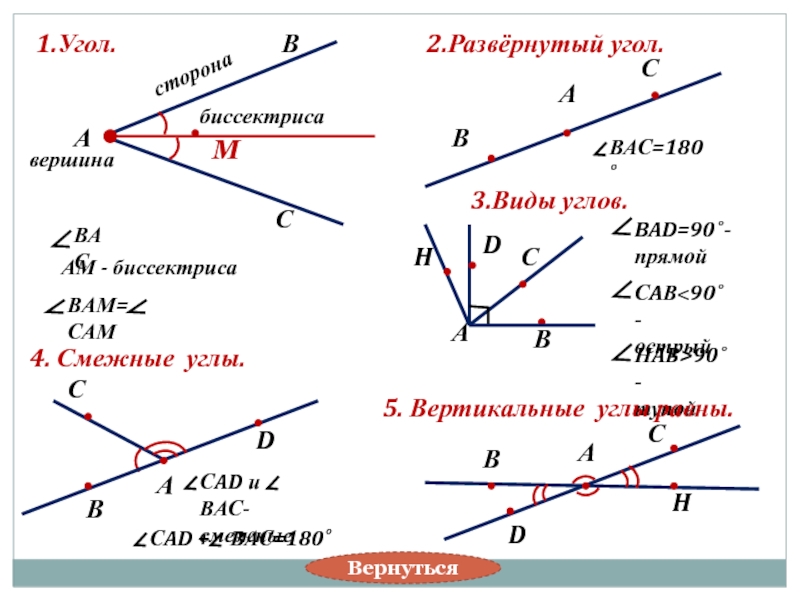
1.Угол.
2.Развёрнутый угол.



В
А
С
3.Виды углов.
ВАС=180˚





В
А
С
В
H
D

BAD=90˚-
прямой

СAВ90˚-
тупой

4. Смежные углы.
5. Вертикальные

углы равны.





В

А

С

D




СAD и ВАС-
смежные



СAD + ВАС=180˚






А

С


H

D








Вернуться

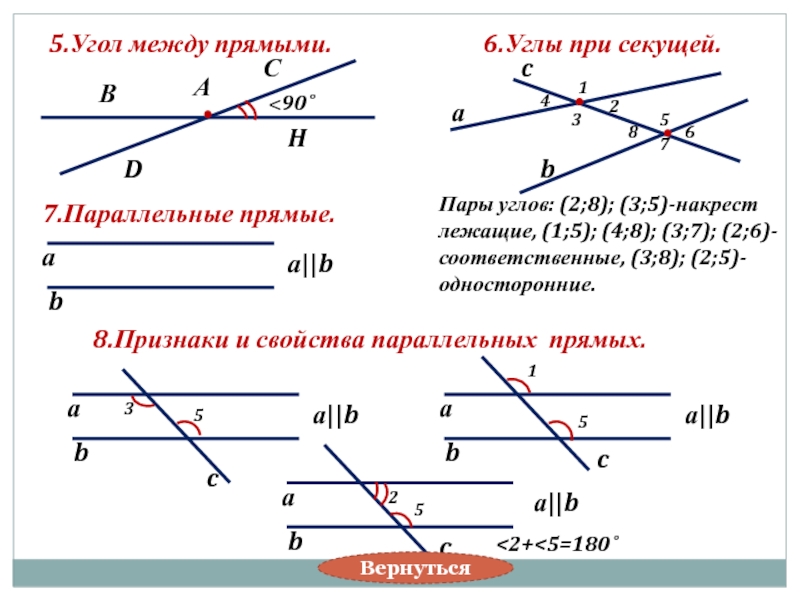
Слайд 75.Угол между прямыми.
В

А
С
H
D


6.Углы при секущей.

(3;7); (2;6)-
соответственные, (3;8); (2;5)-
односторонние.

7.Параллельные прямые.

а

b

а||b

8.Признаки и свойства параллельных прямых.

а

b

а||b

c



3

5

а

b

а||b



1

5

c

а

b

а||b



2

5

c


<2+<5=180˚

Вернуться

Слайд 8Вернуться
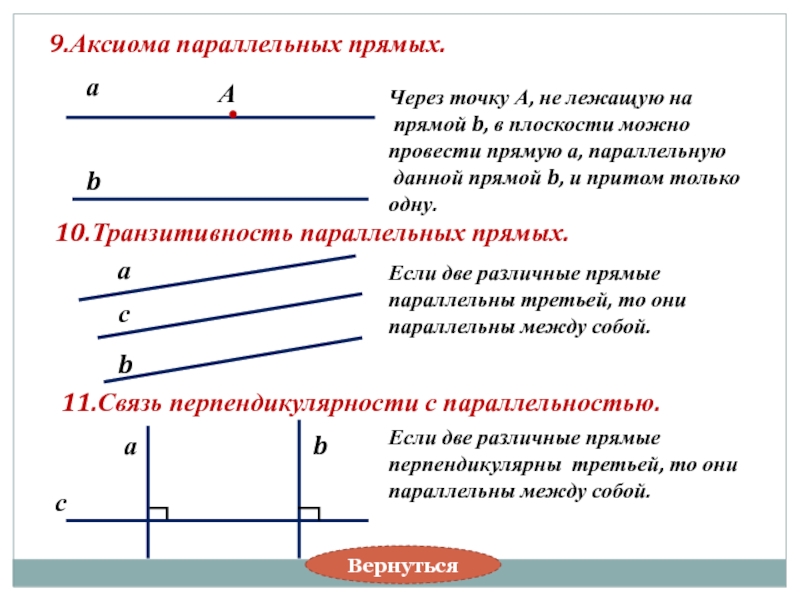
9.Аксиома параллельных прямых.

а
b
А
Через точку А, не лежащую на
прямой b, в

плоскости можно
провести прямую а, параллельную
данной прямой b, и притом только одну.

а

b

с

Если две различные прямые параллельны третьей, то они параллельны между собой.

10.Транзитивность параллельных прямых.

11.Связь перпендикулярности с параллельностью.

а

b

с



Если две различные прямые перпендикулярны третьей, то они параллельны между собой.

Слайд 912. Теорема Фалеса.
А₁
А₂
А₃
А₄
А₅
В₁
В₂
В₃
В₄
В₅
Если на одной из двух прямых
отложить несколько равных
отрезков

и через их концы
провести параллельные прямые
до пересечения с другой прямой,
то и на ней отложатся равные
отрезки .

13. Расширенная теорема
Фалеса.

А₁

А₂

А₃

А₄

В₁

В₂

В₃

В₄

Если на одной из двух прямых
отложить несколько отрезков
и через их концы провести
параллельные прямые до
пересечения с другой прямой,
то и на ней отложатся
отрезки, пропорциональные
данным .

А₁А₂:А₂А₃:А₃А₄=В₁В₂:В₂В₃:В₃В₄

Вернуться

Слайд 10Треугольники.
1.Треугольник, его элементы.
2.Признаки равенства.
3.Подобие.
4. Линейные элементы.
5. Площадь.
6. Теоремы синусов и косинусов.
7.

Вписанная и описанная окружности.

8. Виды.

Вернуться

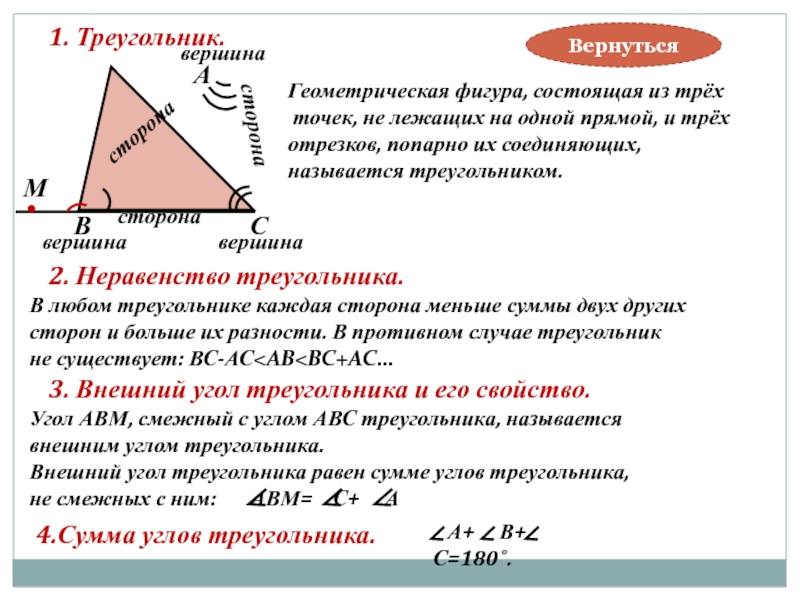
Слайд 11Угол АВМ, смежный с углом АВС треугольника, называется
внешним углом треугольника.


Внешний угол треугольника равен сумме углов треугольника,
не смежных с ним: АВМ= С+ А

1. Треугольник.


В

А

С

Геометрическая фигура, состоящая из трёх
точек, не лежащих на одной прямой, и трёх
отрезков, попарно их соединяющих,
называется треугольником.

2. Неравенство треугольника.

сторона

вершина


сторона

сторона

вершина

вершина






В любом треугольнике каждая сторона меньше суммы двух других
сторон и больше их разности. В противном случае треугольник
не существует: ВС-АС<АВ<ВС+АС…

3. Внешний угол треугольника и его свойство.



М

4.Сумма углов треугольника.




А+ В+ С=180˚.




Вернуться

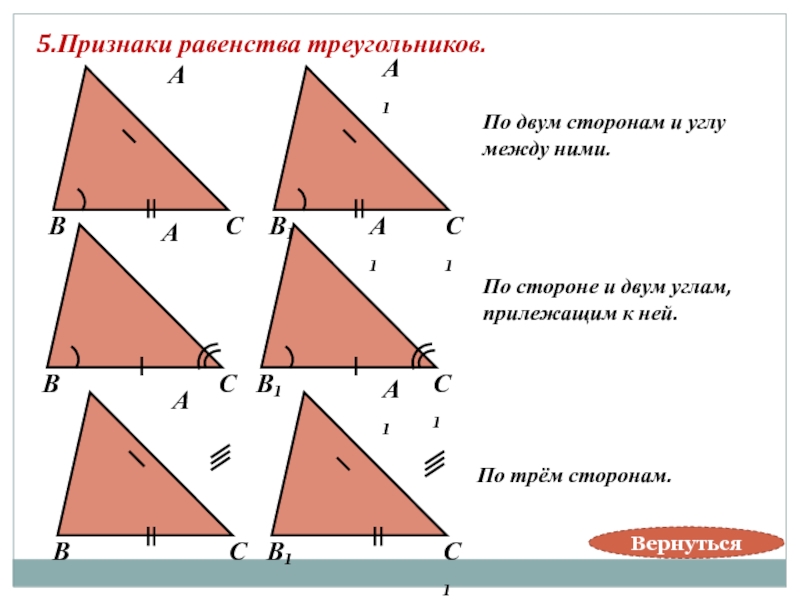
Слайд 125.Признаки равенства треугольников.

В
А
С


В₁
А₁
С₁


В
А
С



В₁
А₁
С₁



В
А
С

В₁
А₁
С₁


По двум сторонам и углу
между ними.
По стороне и двум

углам,
прилежащим к ней.

По трём сторонам.

Вернуться

Слайд 13Подобие треугольников.
1.Признаки подобия.
2.Примеры и свойства.
Вернуться

Слайд 14

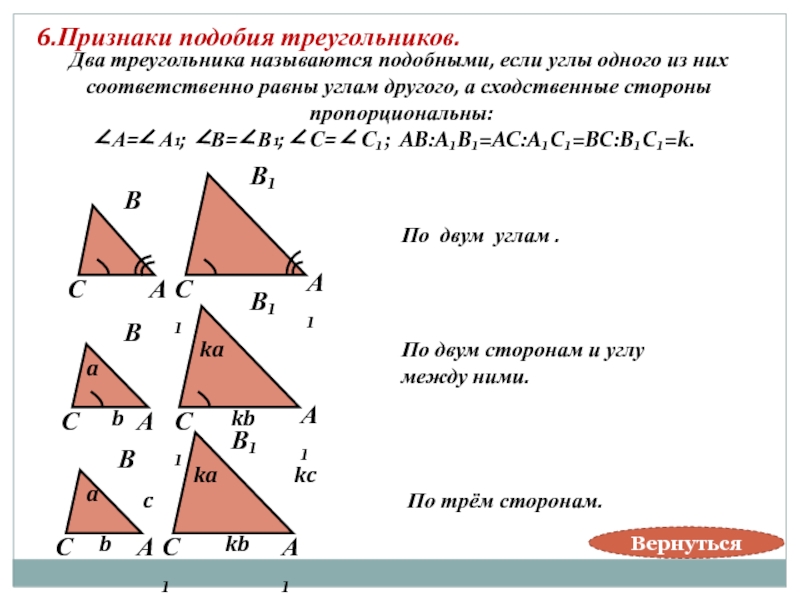
6.Признаки подобия треугольников.
В
А
С
В₁
А₁
С₁
Два треугольника называются подобными, если углы одного из них
соответственно

равны углам другого, а сходственные стороны
пропорциональны:
А= А₁; В= В₁; С= С₁; АВ:А₁В₁=АС:А₁С₁=ВС:В₁С₁=k.















В

А

С

В₁

А₁

С₁





В

А

С

В₁

А₁

С₁

a

b

ka

kb

a

b

kc

c

ka

kb

По двум углам .

По двум сторонам и углу
между ними.

По трём сторонам.

Вернуться

Слайд 157. Примеры и свойства подобных треугольников.

В
А
С
В₁
С₁
Прямая, параллельная стороне треугольника,
отсекает от него

треугольник, подобный данному.

Сходственные биссектрисы, медианы и высоты треугольников
пропорциональны сходственным сторонам.

Отношение периметров подобных треугольников равно отношению
cходственных сторон (коэффициенту подобия k) .

Отношение площадей подобных треугольников равно квадрату
отношения cходственных сторон (квадрату коэффициента
подобия k²) .

Вернуться

Слайд 16Линейные элементы.
1.Медиана.
2.Высота.
Вернуться
3.Биссектриса.
4.Средняя линия.

Слайд 178. Медиана треугольника.

В
А
С
В₁
С₁
А₁

М
Медианой треугольника называется отрезок,
соединяющий вершину треугольника с серединой
противоположной

стороны.

Медианы треугольника пересекаются в одной точке (центре
тяжести треугольника) и делятся ею в отношении 2:1, считая
от вершины: АМ:МА₁=ВМ:МВ₁=СМ:МС₁=2:1.

Медиана треугольника делит его на два равновеликих (с равными
площадями) треугольника.
Все медианы треугольника делят его на 6 равновеликих
треугольников.

Вернуться

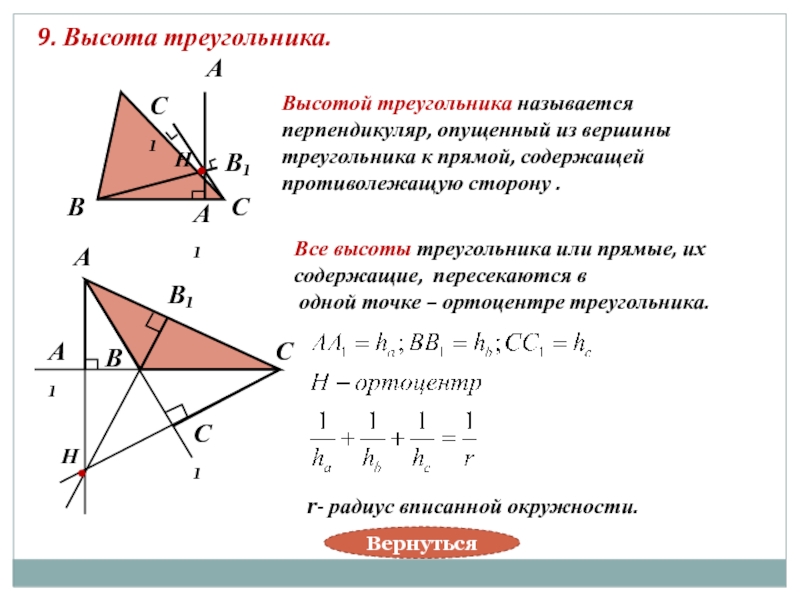
Слайд 189. Высота треугольника.

В
А
С
В₁
С₁
А₁

Н





Н
В
А
С
В₁
С₁
А₁



Высотой треугольника называется
перпендикуляр, опущенный из вершины
треугольника к прямой,

содержащей
противолежащую сторону .

Все высоты треугольника или прямые, их
содержащие, пересекаются в
одной точке – ортоцентре треугольника.

r- радиус вписанной окружности.

Вернуться

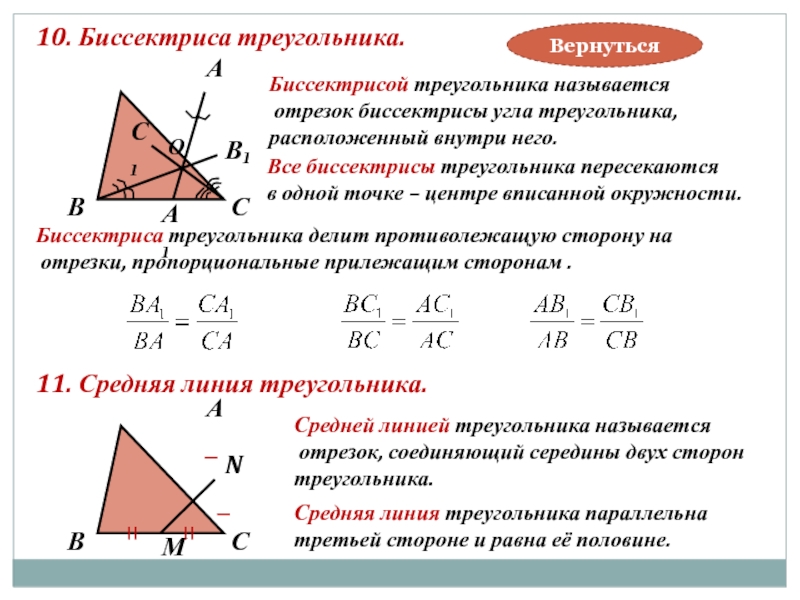
Слайд 1910. Биссектриса треугольника.

В
А
С
В₁
А₁
О
С₁












Биссектрисой треугольника называется
отрезок биссектрисы угла треугольника,
расположенный внутри

него.

Все биссектрисы треугольника пересекаются
в одной точке – центре вписанной окружности.

Биссектриса треугольника делит противолежащую сторону на
отрезки, пропорциональные прилежащим сторонам .

11. Средняя линия треугольника.


В

А

С

М

N

Средней линией треугольника называется
отрезок, соединяющий середины двух сторон
треугольника.

Средняя линия треугольника параллельна
третьей стороне и равна её половине.

Вернуться

Слайд 2012. Площадь треугольника.

В
А
С
a
b
c
r- радиус вписанной окружности.
R- радиус oписанной окружности.
- формула Герона

.

Вернуться



о₁

о₂

r

R

ha




Слайд 2113. Теорема синусов.

В
А
С
a
b
c
Стороны треугольника пропорциональны
синусам противолежащих углов с
коэффициентом пропорциональности,


равным диаметру описанной окружности.

14. Теорема косинусов.

Квадрат стороны треугольника равен сумме квадратов двух
других сторон без удвоенного произведения этих сторон на косинус
угла между ними.

Вернуться

Слайд 22
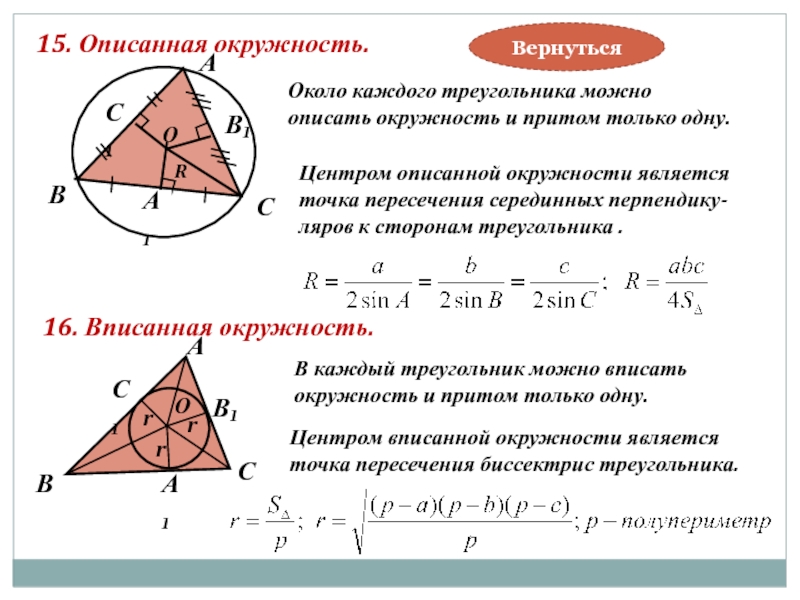
15. Описанная окружность.


В
А
С
В₁
С₁
А₁
О















Около каждого треугольника можно
описать окружность и притом только

одну.

Центром описанной окружности является
точка пересечения серединных перпендику-
ляров к сторонам треугольника .

16. Вписанная окружность.


О

В

А

С

В₁

С₁

А₁

r

r

r

В каждый треугольник можно вписать
окружность и притом только одну.

Центром вписанной окружности является
точка пересечения биссектрис треугольника.

Вернуться

R

Слайд 23Виды треугольников.
1.Прямоугольный.
2.Равнобедренный.
Вернуться
3.Равностороний (правильный).

Слайд 24Прямоугольный треугольник.
1.Определение и свойства.
2.Соотношения.
Вернуться
3.Вписанная и описанная окружности.
4.Площадь.

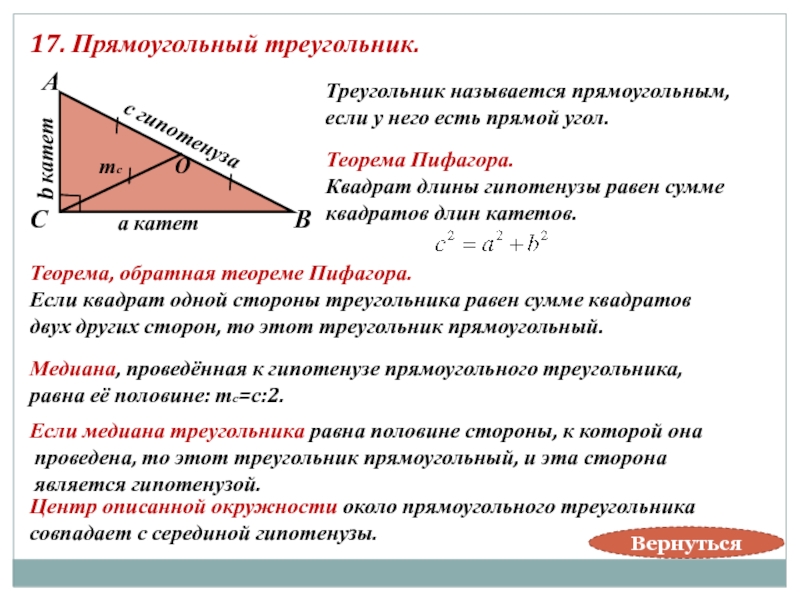
Слайд 2517. Прямоугольный треугольник.

В
А
С
а катет
b катет
с гипотенуза

Треугольник называется прямоугольным,
если у него

есть прямой угол.

Теорема Пифагора.
Квадрат длины гипотенузы равен сумме
квадратов длин катетов.

Медиана, проведённая к гипотенузе прямоугольного треугольника,
равна её половине: тс=с:2.

тс




Если медиана треугольника равна половине стороны, к которой она
проведена, то этот треугольник прямоугольный, и эта сторона
является гипотенузой.

О

Теорема, обратная теореме Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов
двух других сторон, то этот треугольник прямоугольный.

Центр описанной окружности около прямоугольного треугольника
совпадает с серединой гипотенузы.

Вернуться

Слайд 2618. Тригонометрические функции острых углов в
прямоугольном треугольнике.

В
А
С
а
b
с




19.

Средние пропорциональные отрезки.


Н

Катет прямоугольного треугольника является средним
пропорциональным отрезком гипотенузы и проекции этого
катета на гипотенузу.

Высота прямоугольного треугольника, проведённая из вершины
прямого угла является средним пропорциональным отрезком
проекций катетов на гипотенузу:

Вернуться

Слайд 27
20.Вписанная и описанная окружности.
В
А
С
а


О₂
О₁
с
b
R
R
R




r


r

r

21.Площадь.


Н

Вернуться



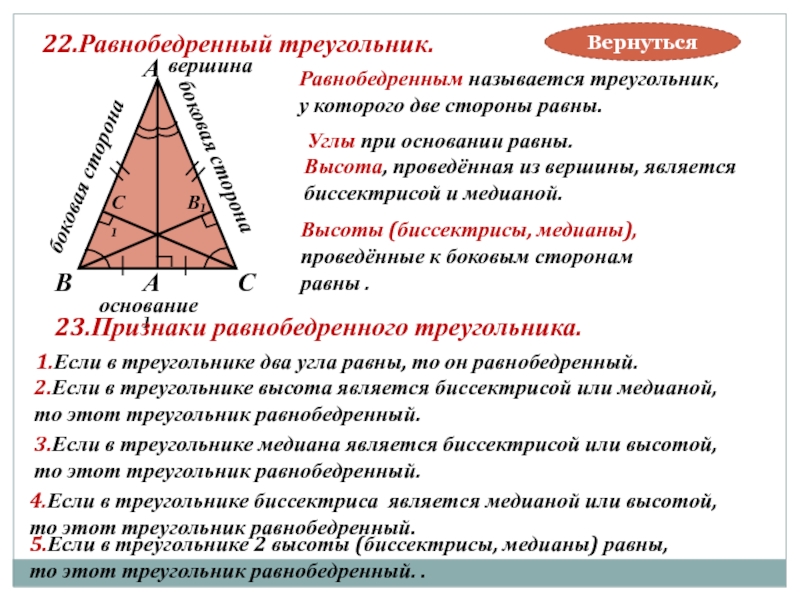
Слайд 2822.Равнобедренный треугольник.

В
А
С
Равнобедренным называется треугольник,
у которого две стороны равны.
вершина
боковая сторона
боковая сторона





Углы

при основании равны.









Высота, проведённая из вершины, является
биссектрисой и медианой.

В₁

С₁

А₁

основание



Высоты (биссектрисы, медианы),
проведённые к боковым сторонам
равны .

23.Признаки равнобедренного треугольника.

1.Если в треугольнике два угла равны, то он равнобедренный.

2.Если в треугольнике высота является биссектрисой или медианой,
то этот треугольник равнобедренный.

3.Если в треугольнике медиана является биссектрисой или высотой,
то этот треугольник равнобедренный.

4.Если в треугольнике биссектриса является медианой или высотой,
то этот треугольник равнобедренный.

5.Если в треугольнике 2 высоты (биссектрисы, медианы) равны,
то этот треугольник равнобедренный. .

Вернуться

Слайд 2924.Равносторонний (правильный) треугольник.

В
А
С
В₁
С₁
А₁












О
Правильным (равносторонним) называется
треугольник, у которого все стороны равны.
25.

Свойства.

1.Все углы равны 60˚.

2. Точки пересечения медиан, биссектрис,
высот, серединных перпендикуляров
совпадают. Эта точка называется центром
треугольника и является центром вписанной
и описанной окружностей.

3. Центр правильного треугольника делит его высоты в отношении
2:1, считая от вершины .

4. Формулы.

5. Площадь.

Вернуться

Слайд 30Параллелограммы.
1.Параллелограмм.
2.Ромб.
Вернуться
3. Прямоугольник.
4.Квадрат.

Слайд 31Параллелограмм.
1.Определение и свойства.
2.Признаки.
Вернуться
4. Метрические соотношения. Площадь.
3.Свойства биссектрис и высот.

Слайд 3226. Определение.

В
А
С
D
О




















Параллелограммом называется
четырёхугольник, у которого
противоположные стороны
попарно параллельны.
27. Свойства.
1.Противоположные углы равны.
3.Противоположные

стороны равны.

2.Односторонние углы в сумме составляют 180˚.

4.Диагонали параллелограмма точкой пересечения делятся
пополам .

1.Если в четырёхугольнике две противоположные стороны равны
и параллельны, то этот четырёхугольник является
параллелограммом

Вернуться

28. Признаки.

2.Если в четырёхугольнике противоположные стороны попарно
равны, то этот четырёхугольник является параллелограммом.

3.Если в четырёхугольнике диагонали точкой пересечения делятся
пополам, то этот четырёхугольник -параллелограмм.

Слайд 3329. Свойства биссектрис и высот.
1.Биссектриса угла (АА₁)отсекает
от параллелограмма
равнобедренный треугольник


( АВ=ВА₁).

2.Биссектрисы односторонних углов перпендикулярны (АА₁ и ВМ), а
биссектрисы противоположных углов параллельны (ВМ и DК)
или лежат на одной прямой (в ромбе)


В

А

С

D





А₁

К

М










3. Высоты параллелограмма
обратно пропорциональны
соответственным сторонам:






В

А

С

D

4.Высоты, опущенные из одной вершины, образуют угол, равный
углу при соседней вершине:

Вернуться

Слайд 34
30. Периметр. Площадь.
В
А
С
D



В
А
С
D


31. Соотношения.
Сумма квадратов диагоналей параллелограмма равна сумме
квадратов четырёх

его сторон:

Вернуться

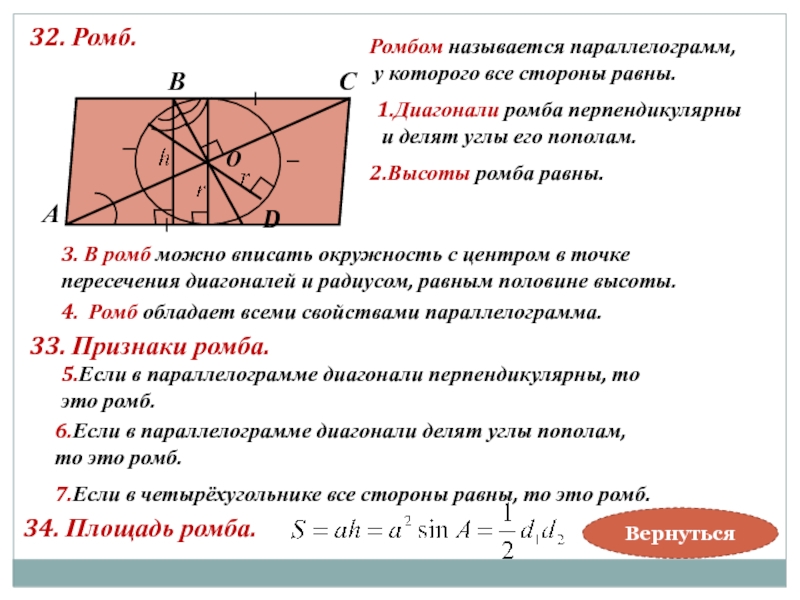
Слайд 3532. Ромб.

В
А
С
D






1.Диагонали ромба перпендикулярны
и делят углы его пополам.
Ромбом называется параллелограмм,

у которого все стороны равны.





О

2.Высоты ромба равны.



3. В ромб можно вписать окружность с центром в точке
пересечения диагоналей и радиусом, равным половине высоты.

4. Ромб обладает всеми свойствами параллелограмма.

33. Признаки ромба.

5.Если в параллелограмме диагонали перпендикулярны, то
это ромб.

6.Если в параллелограмме диагонали делят углы пополам,
то это ромб.

7.Если в четырёхугольнике все стороны равны, то это ромб.

34. Площадь ромба.

Вернуться



Слайд 3635. Прямоугольник.

В
А
С
D




О

Прямоугольником называется
параллелограмм, у которого все
углы прямые.
1.Диагонали прямоугольника равны.

2.Около

прямоугольника можно
описать окружность с центром в
точке пересечения диагоналей и
радиусом, равным половине
диагонали.

3. Прямоугольник обладает всеми
свойствами параллелограмма.

36. Признаки прямоугольника.

1. Если в параллелограмме диагонали равны, то это прямоугольник.

2. Если в параллелограмме один угол прямой, то это прямоугольник.

3. Если в четырёхугольнике есть три прямых угла, то это
прямоугольник.

37. Периметр и площадь прямоугольника.

Вернуться

Слайд 3738. Квадрат.

В
А
С
D

45˚

Квадратом называется прямоугольник,
у которого все стороны равны.
Квадратом называется ромб,

у которого все углы прямые.

Квадрат обладает всеми свойствами
ромба, прямоугольника и
параллелограмма.

Квадрат является правильным четырёхугольником.

d-диагональ,
R-радиус описанной окружности
r- радиус вписанной окружности
a- сторона

Вернуться

Слайд 38Трапеции.
1.Трапеция.
2.Свойства трапеции.
Вернуться
3. Вписанная окружность.
4.Равнобедренная и прямоугольная трапеции.

Слайд 3939. Трапеция.
Вернуться

Трапецией называется четырёхугольник,
две стороны которого параллельны, а
две другие нет.
В
А
С
D

Н
M
N






BC

и AD - верхнее и нижнее основания.

АB и СD –боковые стороны.

АС и ВD –диагонали.

МN – средняя линия.

ВН – высота трапеции, расстояние между основаниями.

Площадь трапеции:

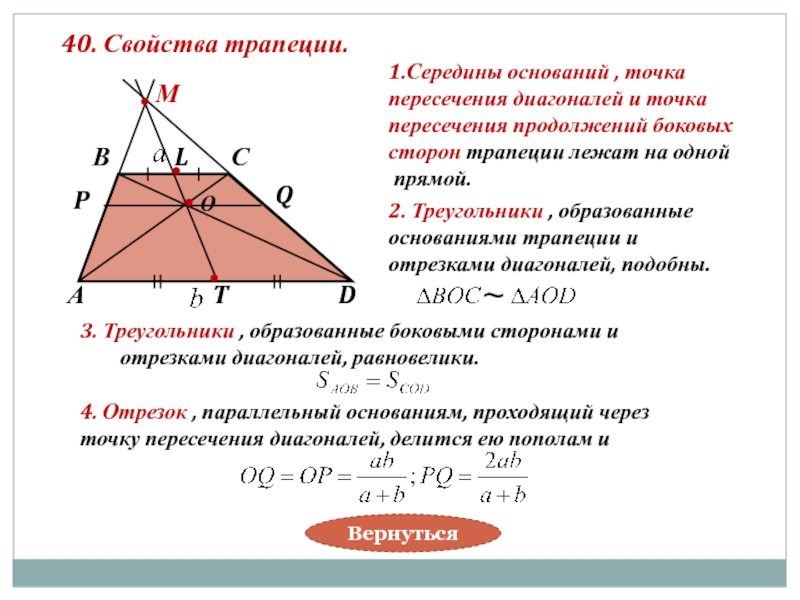
Слайд 4040. Свойства трапеции.







В
А
С
D
L
T

О
1.Середины оснований , точка
пересечения диагоналей и точка
пересечения

продолжений боковых
сторон трапеции лежат на одной
прямой.

2. Треугольники , образованные
основаниями трапеции и
отрезками диагоналей, подобны.

~

3. Треугольники , образованные боковыми сторонами и отрезками диагоналей, равновелики.

4. Отрезок , параллельный основаниям, проходящий через
точку пересечения диагоналей, делится ею пополам и

P

Q

М




Вернуться

Слайд 41
41. Вписанная окружность.

В трапецию можно вписать окружность тогда и только


тогда, когда сумма оснований равна сумме боковых сторон.

Центром вписанной окружности
является точка пересечения
биссектрис углов трапеции и радиус
этой окружности

О












В

А

С

D

BC+AD=AB+CD.

Вернуться

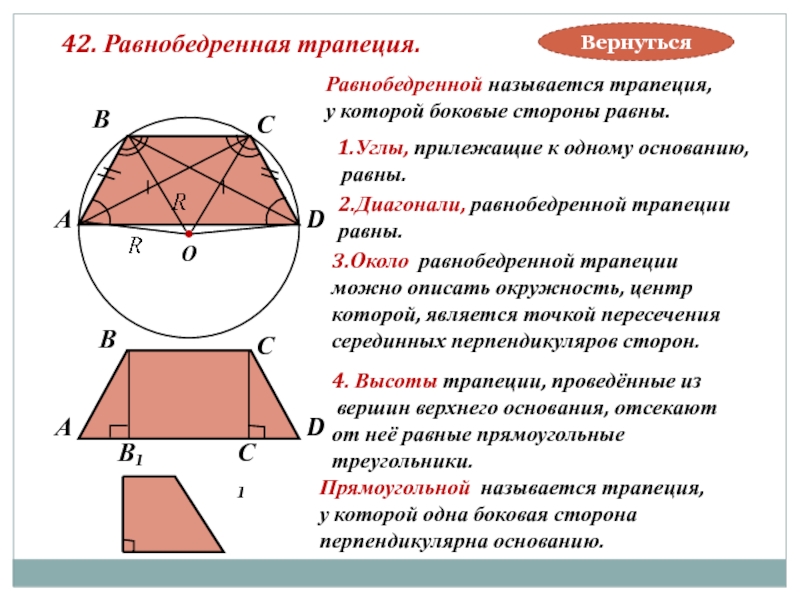
Слайд 4242. Равнобедренная трапеция.









В
А
С
D


О
Равнобедренной называется трапеция,
у которой боковые стороны равны.




1.Углы, прилежащие к

одному основанию,
равны.

2.Диагонали, равнобедренной трапеции
равны.

3.Около равнобедренной трапеции
можно описать окружность, центр
которой, является точкой пересечения
серединных перпендикуляров сторон.


В

А

С

D

В₁

С₁



4. Высоты трапеции, проведённые из
вершин верхнего основания, отсекают
от неё равные прямоугольные
треугольники.




Прямоугольной называется трапеция,
у которой одна боковая сторона
перпендикулярна основанию.

Вернуться

Слайд 43Окружность.
1.Отрезки и дуги.
2.Прямая и окружность.
Вернуться
3. Углы в окружности.
5.Вписанная окружность.
6.Описанная окружность.
4.Две окружности.
7.Общие

касательные двух окружностей.

8. Круг и его части.

Слайд 44Отрезки и дуги.
1.Отрезки и дуги.
Вернуться
2.Свойства отрезков и дуг.

Слайд 4543. Отрезки и дуги.


О
М
Окружностью называется множество
точек плоскости, находящихся на
одинаковом

расстоянии от данной точки О
(центра окружности).

Хордой называется отрезок, соединяющий две точки окружности (PQ и AB).

Диаметром называется хорда, проходящая через центр (АВ).

Радиусом называется отрезок (ОМ),
соединяющий точку окружности с
центром.

Дугой называется часть окружности, заключённая между двумя
её точками.

Q

P

N

Две точки на окружности образуют на ней две дуги: PNQ и PMQ
Любую из них стягивает хорда PQ .

Длина окружности С=2πR.

Длина дуги окружности l=πRα/180.

α-градусная мера дуги

l=Rα, α- радианная мера дуги.

Вернуться

В

А

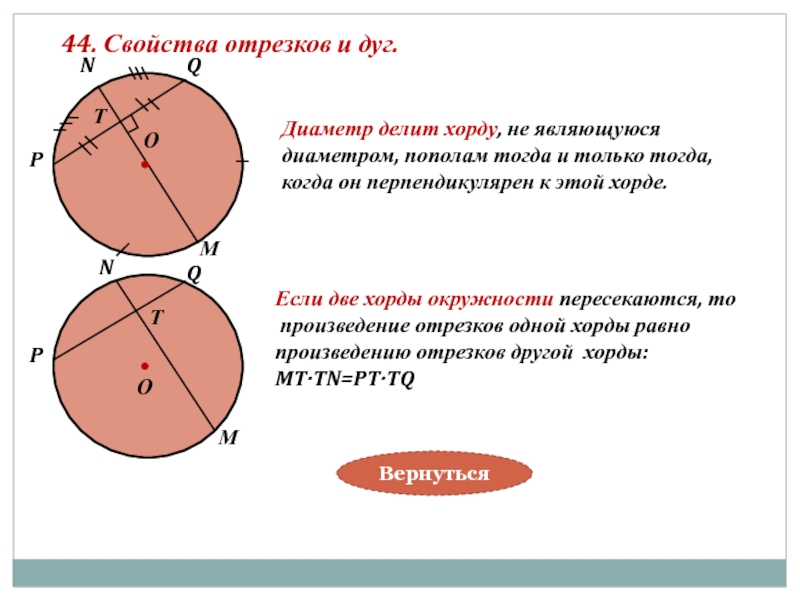
Слайд 4644. Свойства отрезков и дуг.

О
М
Q
P
N

Диаметр делит хорду, не являющуюся
диаметром, пополам

тогда и только тогда,
когда он перпендикулярен к этой хорде.

Т




О

Если две хорды окружности пересекаются, то
произведение отрезков одной хорды равно
произведению отрезков другой хорды:
MT·TN=PT·TQ

М

Q

P

N

Т

Вернуться

Слайд 47Прямая и окружность.
1.Прямая и окружность.
Вернуться
2. Окружность и две прямые.

Слайд 4844. Прямая и окружность.


О

М
М
М
ОМ- расстояние от центра окружности
до прямой.
Если ОМ

окружность и прямая имеют
две общие точки: P и Q. И прямая называется
секущей окружности.

Q

P

Если ОМ=R, то окружность и прямая имеют
одну общую точку: М. И прямая называется
касательной к окружности, а точка М –
точкой касания.

Если ОМ>R, то окружность и прямая не имеют общих точек,
не пересекаются.

45. Признак касательной.

Прямая является касательной к окружности, тогда и только
тогда, когда радиус, проведённый в их общую точку,
перпендикулярен прямой

Вернуться

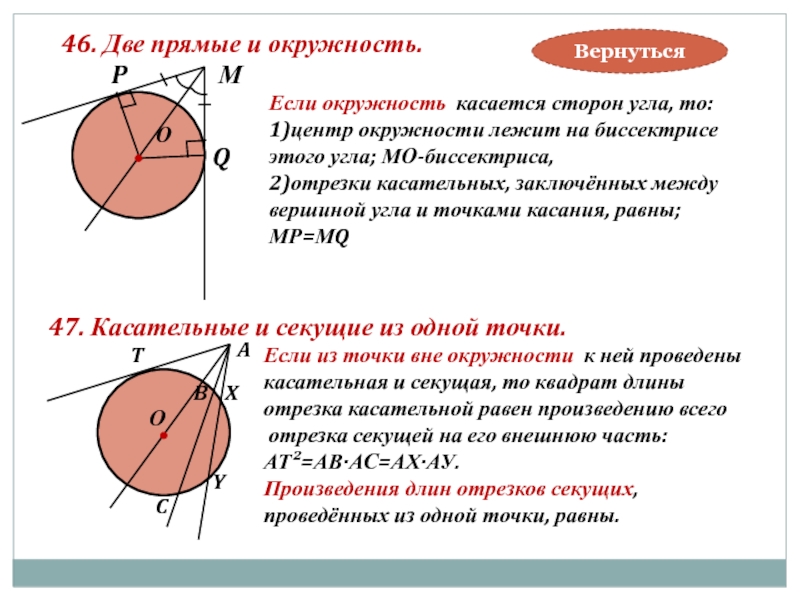
Слайд 4946. Две прямые и окружность.

О
М
Если окружность касается сторон угла, то:
1)центр окружности

лежит на биссектрисе
этого угла; МО-биссектриса,
2)отрезки касательных, заключённых между
вершиной угла и точками касания, равны;
МР=МQ

Q

P

47. Касательные и секущие из одной точки.

Вернуться








A

T

Y

X

C

B

О

Если из точки вне окружности к ней проведены
касательная и секущая, то квадрат длины
отрезка касательной равен произведению всего
отрезка секущей на его внешнюю часть:
АТ²=АВ·АС=АХ·АУ.
Произведения длин отрезков секущих,
проведённых из одной точки, равны.

Слайд 50
48.Цнтральный угол.
С
В

О
Если вершина угла находится в центре
окружности, а стороны его

пересекают
окружность, то этот угол называется
центральным (ВОС).

Градусная мера дуги (ВС), заключённой внутри
центрального угла, равна градусной мере
этого центрального угла.

α˚

α˚

49.Вписанный угол.

А

α˚/2

Если вершина угла находится на окружности, а стороны его
пересекают окружность, то этот угол называется
вписанным в окружность (ВАС).

Вписанный угол равен половине градусной меры дуги, заключённой
внутри его (на которую он опирается).

К

Вернуться

Вписанный угол (РКМ), опирающийся на полуокружность
(диаметр) равен 90˚ (прямой).


М

P

Далее

Слайд 51Градусная мера угла (ВКС), стороны которого пересекают
окружность, а вершина находится

вне её, равна полу разности
градусных мер дуг, заключённых внутри этого угла (В₁С₁ и ВРС).

Вернуться

50.Свойства вписанных углов.


С

В

А

К

Вписанные углы, опирающиеся на одну и
ту же дугу равны.



М

51.Другие углы.

Р

Вписанные углы, опирающиеся на одну и
ту же хорду или равны (ВАС и ВМС), или
их сумма равна 180˚ (ВРС и ВМС).

D

Градусная мера угла (СAD), между хордой и касательной равна
половине дуги, заключённой внутри этого угла (дуги АМС).

Т

Градусная мера угла (ВТС), вершина которого лежит внутри
окружности , а стороны пересекают её равна полу сумме
градусных мер дуг, заключённых внутри этого угла и внутри
вертикального ему угла (дуг ВРС и С₁АМ).

В₁

С₁

Слайд 52




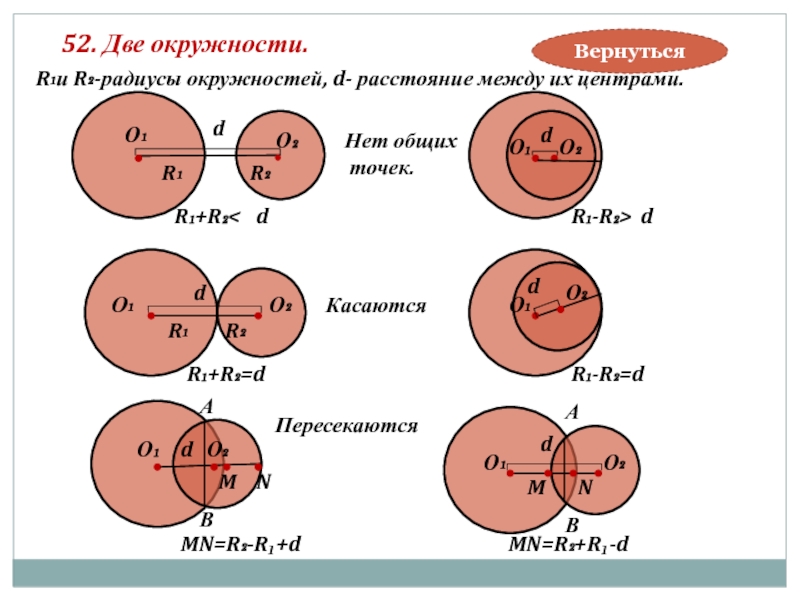
52. Две окружности.
Вернуться
О₁

О₂


d
R₁
R₂
R₁+R₂

d




О₁
О₂

d
R₁+R₂=d



R₂


О₁
О₂
d
R₁-R₂=d






О₁
О₂
d
MN=R₂-R₁+d



В
А


M
N
О₂




О₁
В
А
M
N

d
MN=R₂+R₁-d

R₁и R₂-радиусы окружностей, d- расстояние между их центрами.

Нет общих

точек.

Касаются

Пересекаются

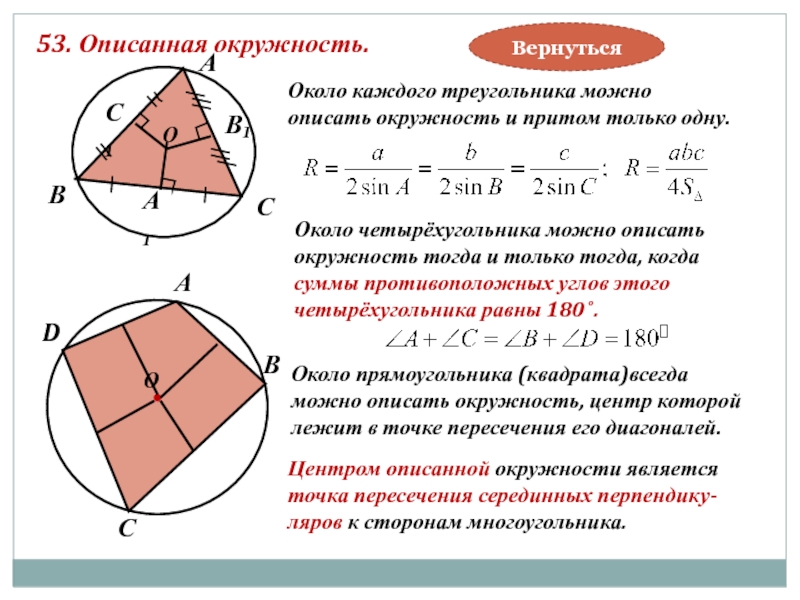
Слайд 5353. Описанная окружность.


В
А
С
В₁
С₁
А₁
О















Около каждого треугольника можно
описать окружность и притом только

одну.

Центром описанной окружности является
точка пересечения серединных перпендику-
ляров к сторонам многоугольника.

Около четырёхугольника можно описать
окружность тогда и только тогда, когда
суммы противоположных углов этого
четырёхугольника равны 180˚.

Около прямоугольника (квадрата)всегда
можно описать окружность, центр которой
лежит в точке пересечения его диагоналей.

Вернуться



В

А

С

D

О


Слайд 54


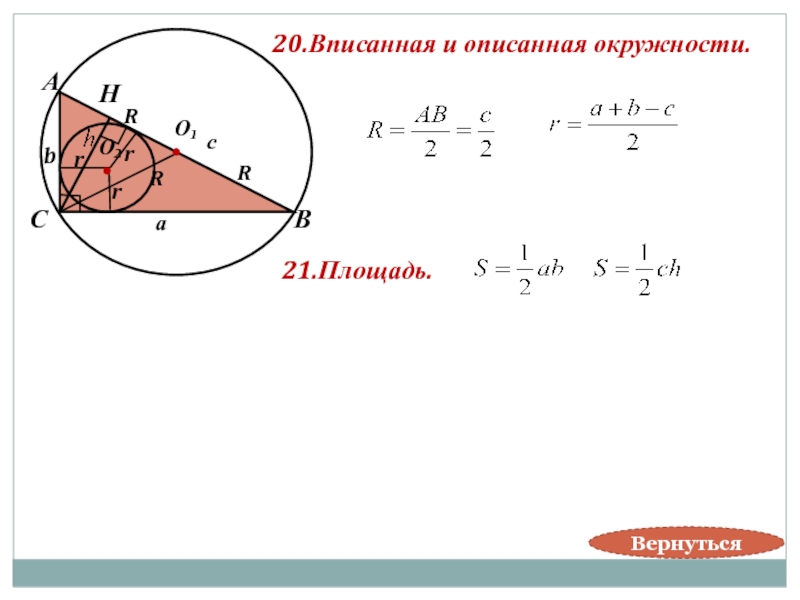
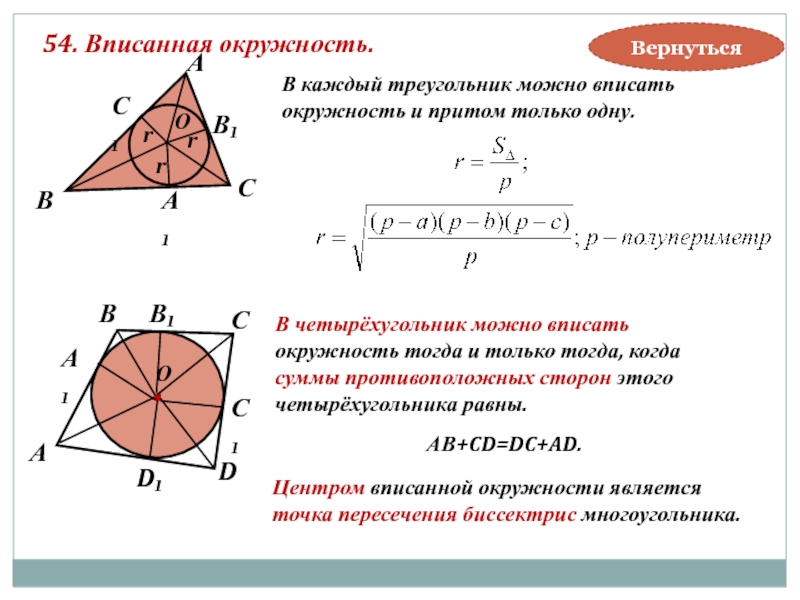
54. Вписанная окружность.

О
В
А
С
В₁
С₁
А₁
r
r
r
В каждый треугольник можно вписать
окружность и притом только

одну.

Центром вписанной окружности является
точка пересечения биссектрис многоугольника.

О



В

А

С

D

В₁

С₁

А₁

D₁

В четырёхугольник можно вписать
окружность тогда и только тогда, когда
суммы противоположных сторон этого
четырёхугольника равны.

АВ+CD=DC+AD.

Вернуться

Слайд 55


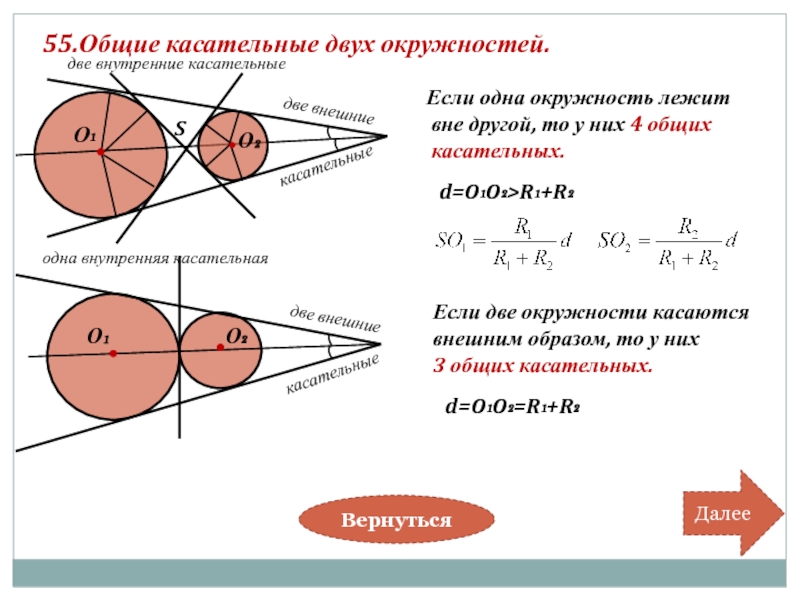
55.Общие касательные двух окружностей.
О₁

О₂

Если одна окружность лежит
вне другой, то у

них 4 общих
касательных.


О₁


О₂






две внутренние касательные

две внешние

касательные

две внешние

касательные

одна внутренняя касательная

Если две окружности касаются
внешним образом, то у них
3 общих касательных.

d=O₁O₂>R₁+R₂

S

d=O₁O₂=R₁+R₂

Далее

Вернуться

Слайд 56

О₁
О₂
d


M

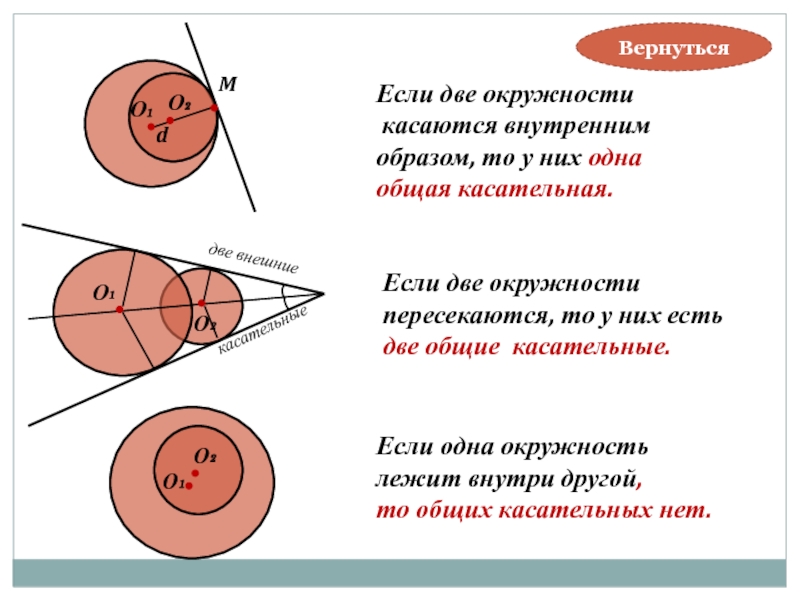
Если две окружности
касаются внутренним
образом, то у них одна
общая

касательная.



О₁


О₂


две внешние

касательные

Если две окружности
пересекаются, то у них есть
две общие касательные.





О₁

О₂



Если одна окружность
лежит внутри другой,
то общих касательных нет.

Вернуться

Слайд 57


сектор
сектор
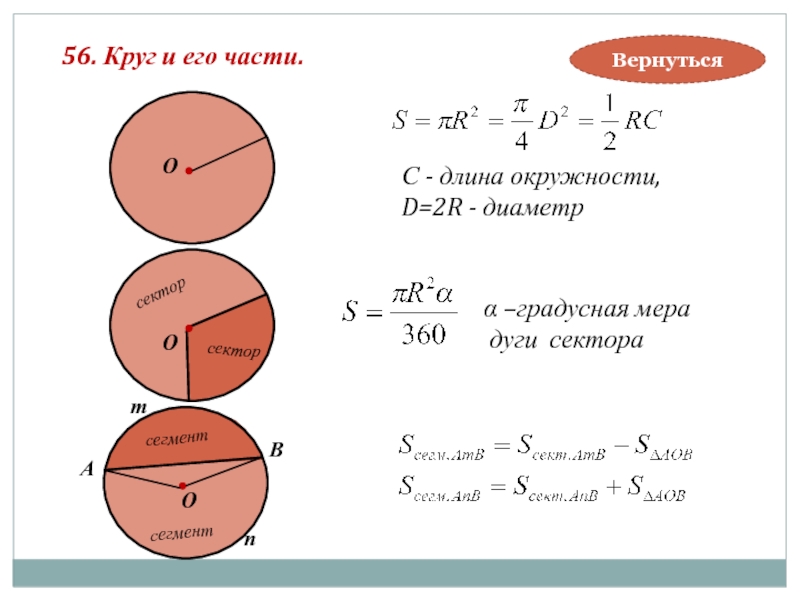
56. Круг и его части.

О

О



О
сегмент
сегмент
В
А
т
С - длина окружности,
D=2R - диаметр
α –градусная

мера
дуги сектора

п

Вернуться

Слайд 58Площади.
1.Площадь треугольника.
Вернуться
2.Отношения площадей.
3.Площадь четырёхугольника.
4.Площадь круга и его частей.
5.Площади правильных многоугольников.

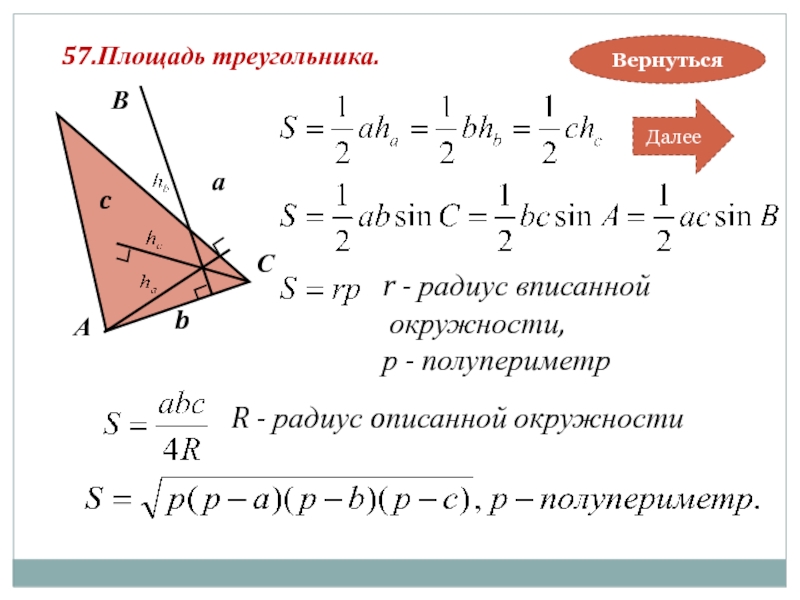
Слайд 5957.Площадь треугольника.




В
А
С
r - радиус вписанной
окружности,
р - полупериметр
R - радиус oписанной

окружности

а

b

c

Вернуться

Далее

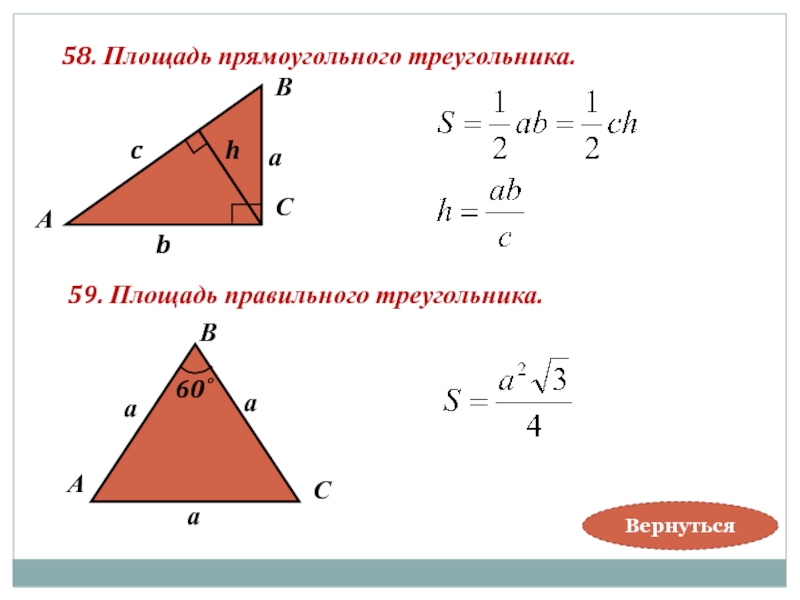
Слайд 6058. Площадь прямоугольного треугольника.

В
А
С

а
b
c
h

59. Площадь правильного треугольника.

В
А
С
а
а
а
60˚

Вернуться

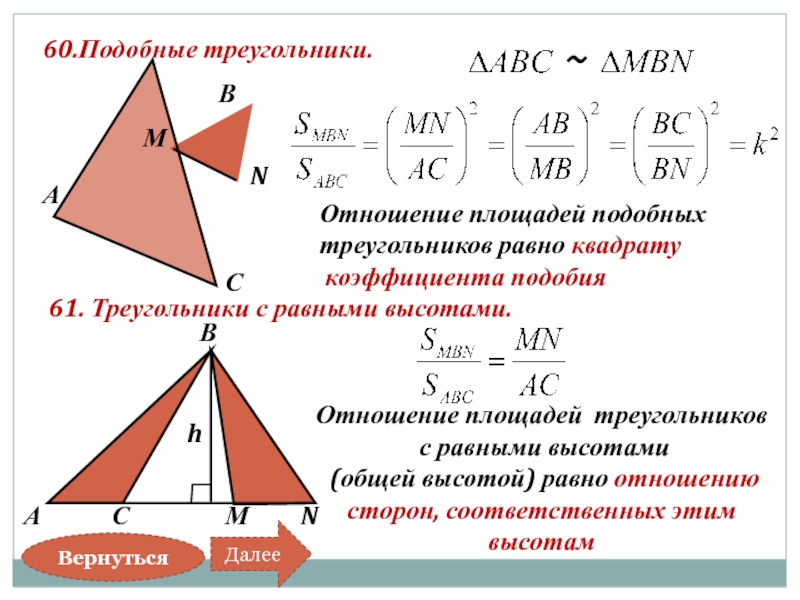
Слайд 61Отношение площадей треугольников
с равными высотами
(общей высотой) равно отношению
сторон, соответственных

этим высотам


60.Подобные треугольники.


В

А

С

М

N

~



Отношение площадей подобных
треугольников равно квадрату
коэффициента подобия

h


В

А

С

М

N

Вернуться

Далее

61. Треугольники с равными высотами.

Слайд 62
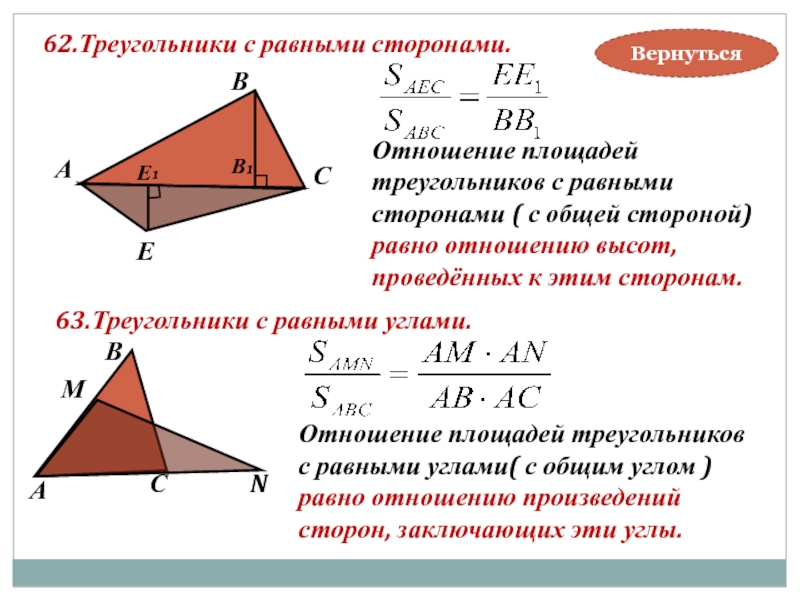
62.Треугольники с равными сторонами.


В
А
С
Е
В₁
Е₁


Отношение площадей
треугольников с равными
сторонами ( с общей

стороной)
равно отношению высот,
проведённых к этим сторонам.


В

А

С

М

N

Отношение площадей треугольников
с равными углами( с общим углом )
равно отношению произведений
сторон, заключающих эти углы.

63.Треугольники с равными углами.

Вернуться

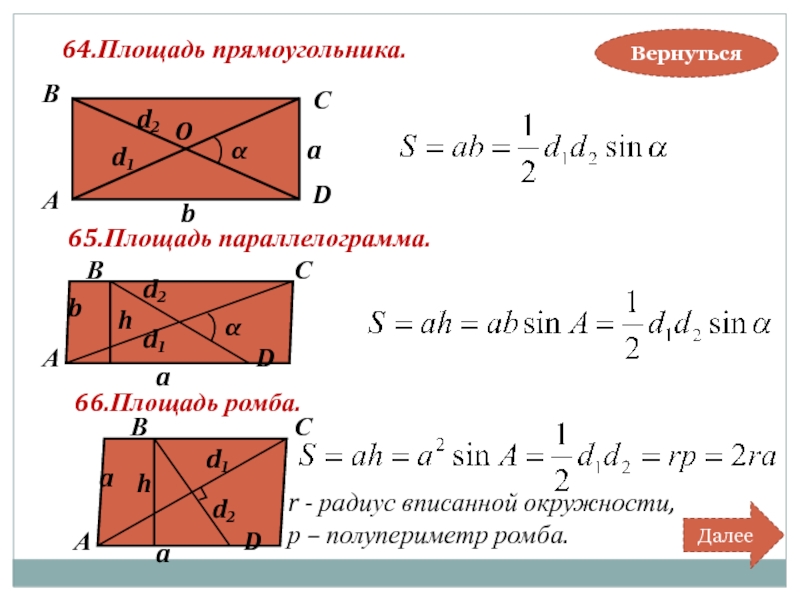
Слайд 6364.Площадь прямоугольника.

В
А
С
D
O

α
a
b
d₂
d₁

В
А
С
D
a
h

α
d₂
d₁
b
66.Площадь ромба.
65.Площадь параллелограмма.

В
А
С
D
a
h
d₂
d₁
a

r - радиус вписанной окружности,
р – полупериметр ромба.
Вернуться
Далее

Слайд 64

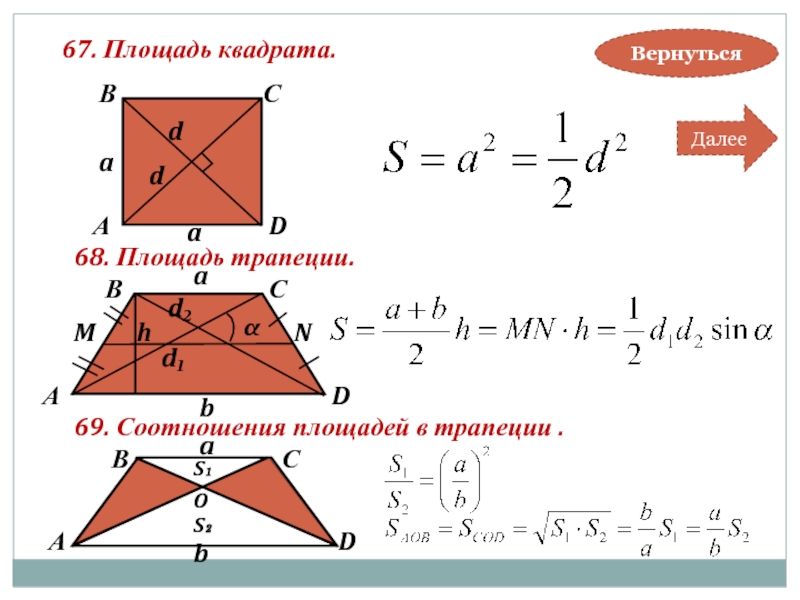
67. Площадь квадрата.

В
А
С
D
a
d
a
d

68. Площадь трапеции.

В
А
С
D
a
b
h

α
d₂
d₁
N
M
69. Соотношения площадей в трапеции .

O
В
А
С
D
a
b
S₁
S₂
Далее
Вернуться

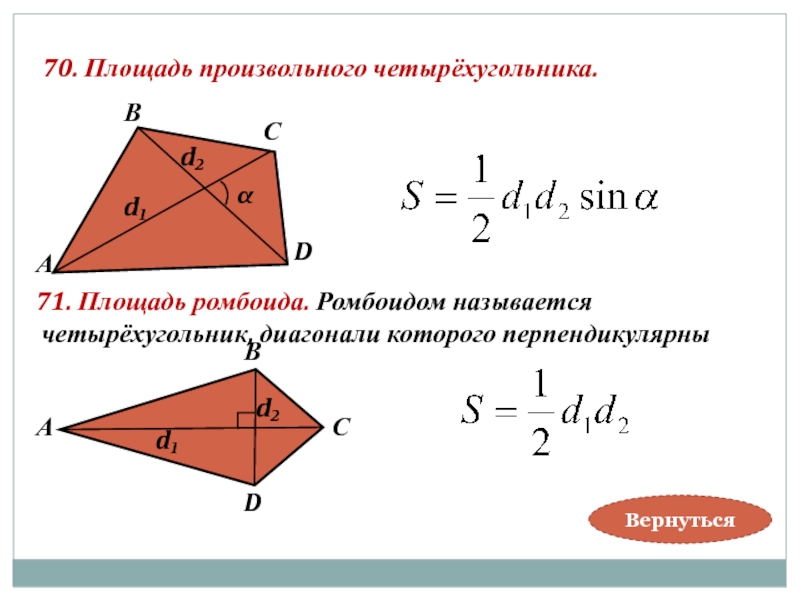
Слайд 6570. Площадь произвольного четырёхугольника.


α
d₂
d₁
В
А
С
D
71. Площадь ромбоида. Ромбоидом называется
четырёхугольник, диагонали которого

перпендикулярны



d₂

d₁

В

А

С

D

Вернуться

Слайд 66


сектор
сектор
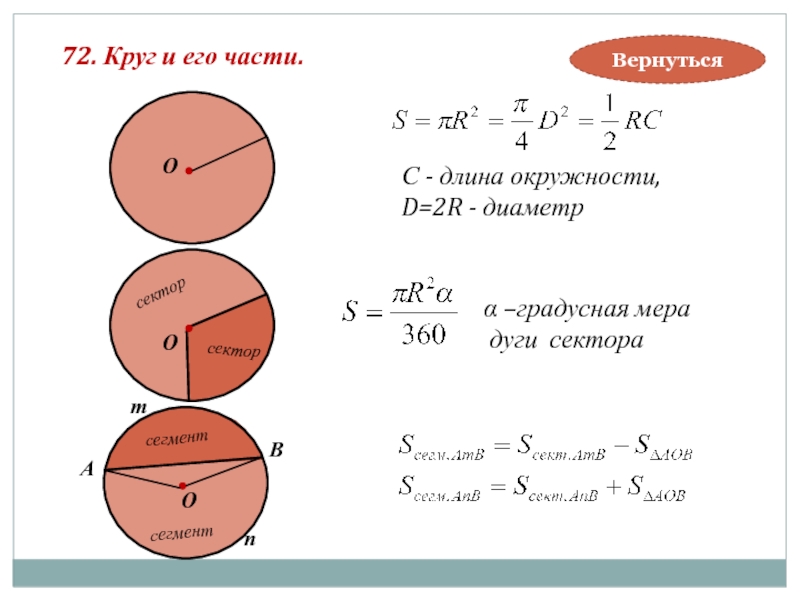
72. Круг и его части.

О

О



О
сегмент
сегмент
В
А
т
С - длина окружности,
D=2R - диаметр
α –градусная

мера
дуги сектора

п

Вернуться

Слайд 67
. . .
73. Площадь правильного п-угольника через радиус
вписанной окружности.
О

А₁
А₂
А₃
А₄
Аn
. .

.

Аk

Аk+1

. . .

. . .



α=2π|n

a

R

r



r - радиус вписанной
окружности,
P – периметр.

Вернуться

Далее

Слайд 68
. . .
74. Площадь правильного п-угольника через радиус
oписанной окружности.
О

А₁
А₂
А₃
А₄
Аn
. .

.

Аk

Аk+1

. . .

. . .



α=2π|n

a

R

r



R - радиус oписанной
окружности.

Вернуться

Слайд 69
. . .
75. Правильный п-угольник.
О

А₁
А₂
А₃
А₄
Аn
. . .
Аk
Аk+1
. . .
. . .


α=2π|n
a
R
r


R

- радиус oписанной
окружности, r-радиус
вписанной окружности,
а-сторона.

Вернуться

Правильным называется
п-угольник, стороны и углы которого равны .

В правильный п-угольник
можно вписать и около него можно описать окружность с центром в точке пересечения биссектрис его углов.


Далее

Слайд 7076. Частные случаи правильных п-угольников.



О

R
r
О

R
r
О

R
r
a
a
a
Вернуться



Слайд 71Закрыть

Похожие презентации

Производная сложной функции 1218
Числовые последовательности. Бесконечно большие и бесконечно малые последовательности. (Лекция 1) 370
Простейшие переборные задачи. Генерация подмножеств и перестановок 302
Дроби 516
Построение линии конуса плоскостью общего положения 280
prezentatsiya po matem 400

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика