- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Способы описания САУ (Математическое описание) презентация
Содержание
- 1. Способы описания САУ (Математическое описание)
- 2. Математическое описание САУ Предпосылка для количественной оценки
- 3. Математическое описание САУ с помощью дифференциальных уравнений
- 4. Математическое описание САУ с помощью дифференциальных уравнений
- 5. Математическое описание САУ с помощью дифференциальных уравнений
- 6. Математическое описание САУ с помощью дифференциальных уравнений
- 7. Математическое описание САУ с помощью дифференциальных уравнений
- 8. Математическое описание САУ с помощью дифференциальных уравнений
- 9. Математическое описание САУ с помощью передаточных функций
- 10. Математическое описание САУ с помощью передаточных функций
- 11. Математическое описание САУ с помощью передаточных функций
- 12. Математическое описание САУ с помощью передаточных функций
- 13. Математическое описание САУ с помощью передаточных функций
- 14. Математическое описание САУ с помощью передаточных функций
- 15. Математическое описание САУ с помощью передаточных функций
- 16. Математическое описание САУ с помощью передаточных функций
- 17. Математическое описание САУ с помощью передаточных функций
- 18. Математическое описание САУ с помощью временных характеристик
- 19. Математическое описание САУ с помощью временных характеристик
- 20. Математическое описание САУ с помощью временных характеристик
- 21. Математическое описание САУ с помощью временных характеристик
- 22. Математическое описание САУ с помощью частотных характеристик
- 23. Математическое описание САУ с помощью частотных характеристик
- 24. Математическое описание САУ с помощью частотных характеристик
- 25. Математическое описание САУ с помощью частотных характеристик
- 26. Математическое описание САУ с помощью частотных характеристик
- 27. Математическое описание САУ с помощью частотных характеристик
- 28. Математическое описание САУ с помощью частотных характеристик
- 29. Математическое описание САУ с помощью частотных характеристик
- 30. Математическое описание САУ с помощью частотных характеристик
- 31. Типовые динамические звенья САУ
- 32. Типовые динамические звенья САУ При расчёте САУ
- 33. Типовые динамические звенья САУ На практике используют
- 34. Типовые динамические звенья САУ 1) Усилительное звено
- 35. Типовые динамические звенья САУ 2) Апериодическое звено
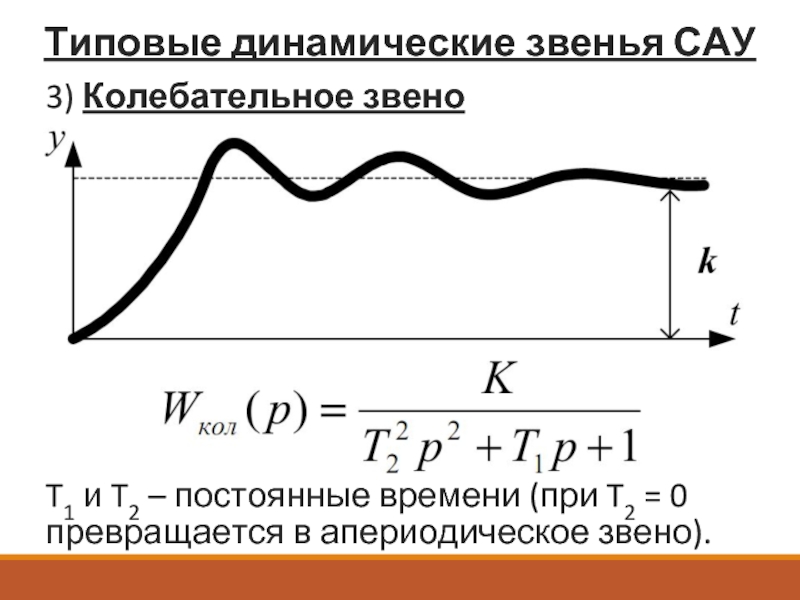
- 36. Типовые динамические звенья САУ 3) Колебательное звено
- 37. Типовые динамические звенья САУ 3) Колебательное звено
- 38. Типовые динамические звенья САУ 4) Интегрирующее звено – выходная величина пропорциональна интегралу от входной.
- 39. Типовые динамические звенья САУ 5) Дифференцирующее звено
- 40. Типовые динамические звенья САУ 6) Запаздывающее звено
Слайд 2Математическое описание САУ
Предпосылка для количественной оценки работы и функционирования САУ.
Динамические характеристики
ДХ САУ могут быть описаны:
дифференциальными уравнениями;
передаточными функциями;
временными характеристиками;
частотными характеристиками.
Слайд 3Математическое описание САУ с помощью дифференциальных уравнений
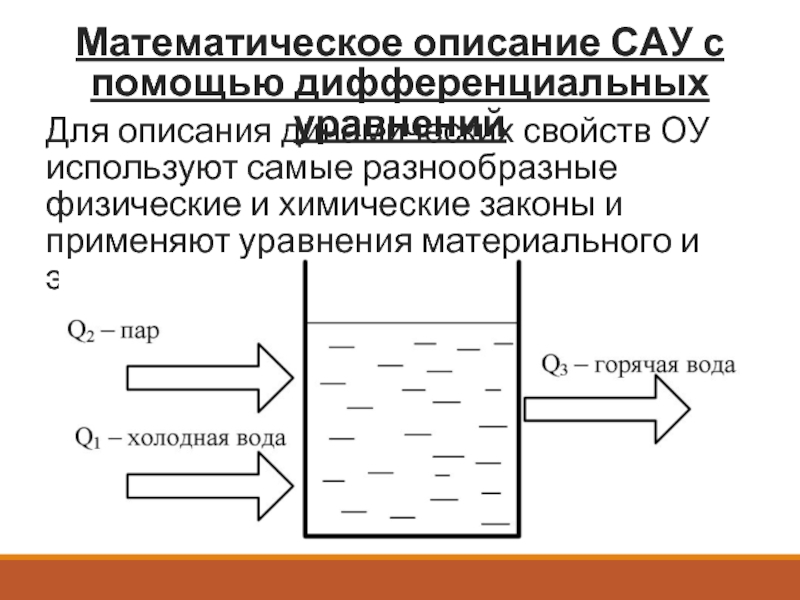
Для описания динамических свойств ОУ
Слайд 4Математическое описание САУ с помощью дифференциальных уравнений
а) установившийся режим
Q1 + Q2
Θ = const
Θ – температура горячей воды.
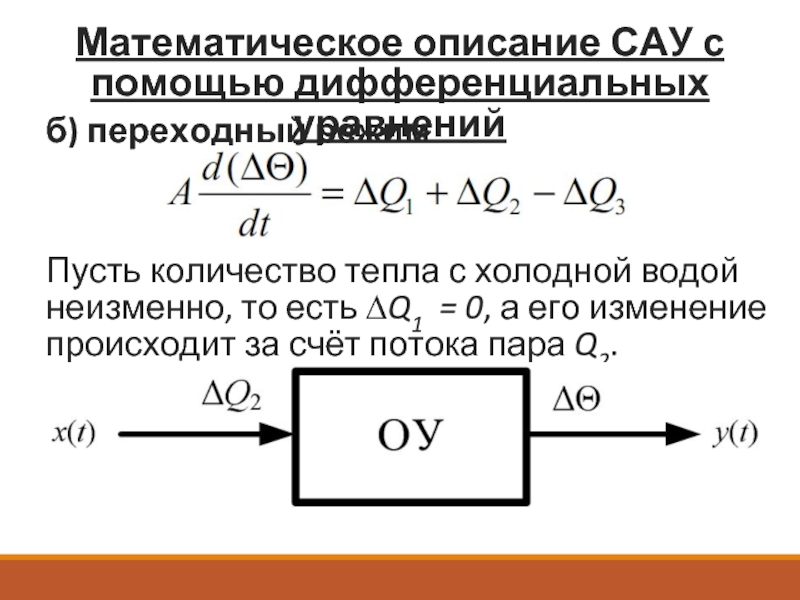
б) переходный режим
возникает при изменении любого потока;
скорость изменения температуры горячей воды Θ зависит от величины изменения теплового потока и коэффициента A (тепловой емкости ОУ)
Слайд 5Математическое описание САУ с помощью дифференциальных уравнений
б) переходный режим
Пусть количество тепла
Слайд 6Математическое описание САУ с помощью дифференциальных уравнений
б) переходный режим
Изменение теплового потока
Слайд 7Математическое описание САУ с помощью дифференциальных уравнений
б) переходный режим
Введем обозначения:
T =
K = 1 / (c • m) – коэффициент передачи ОУ
y = ∆Θ x = ∆Q2
- дифференциальное уравнение 1 порядка
Слайд 8Математическое описание САУ с помощью дифференциальных уравнений
В общем случае САУ может
Решение дифференциальных уравнений высокого порядка вызывает значительные трудности. Поэтому применяется форма записи дифференциальных уравнений в виде передаточных функций.
Слайд 9Математическое описание САУ с помощью передаточных функций
Передаточная функция – это особая
Преобразование Лапласа позволяют представить функцию вещественного переменного (времени) как функцию комплексного переменного.
Слайд 10Математическое описание САУ с помощью передаточных функций
Преобразование осуществляется с помощью прямого
где x(t) – называют оригиналом;
x(p) – изображением.
Если известно x(p) и требуется найти функцию времени, то оригинал находят по правилу обратного преобразования Лапласа, т.е.
Слайд 11Математическое описание САУ с помощью передаточных функций
Основные свойства преобразования Лапласа:
1. Умножение
2. Суммирование оригиналов соответствует суммированию изображений:
Слайд 12Математическое описание САУ с помощью передаточных функций
Основные свойства преобразования Лапласа:
3. Дифференцированию
Слайд 13Математическое описание САУ с помощью передаточных функций
Основные свойства преобразования Лапласа:
3. Дифференцированию
Слайд 14Математическое описание САУ с помощью передаточных функций
Основные свойства преобразования Лапласа:
При нулевых
Слайд 15Математическое описание САУ с помощью передаточных функций
Основные свойства преобразования Лапласа:
Интегрирование оригинала
Пользуясь свойством Лапласа 1, 2, 3 при нулевых начальных условиях уравнение (*) приводится к виду:
Слайд 16Математическое описание САУ с помощью передаточных функций
Основная трудность не в решении
Прямое и обратное преобразование Лапласа осуществляют с помощью таблиц оригиналов и изображений [в специальных справочниках].
Уравнение алгебраическое (**) в изображениях несет такую же информацию о динамике системы, как и дифференциальное.
Слайд 17Математическое описание САУ с помощью передаточных функций
Отношение W(p) = y(p)/x(p) называют
Передаточные функции получили очень широкое распространение в САУ при расчете систем.
Слайд 18Математическое описание САУ с помощью временных характеристик
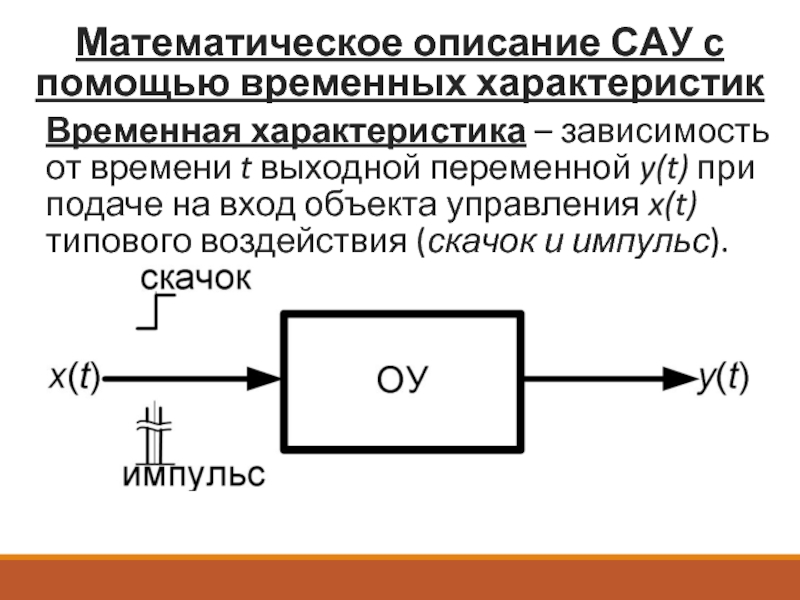
Временная характеристика – зависимость от
Слайд 19Математическое описание САУ с помощью временных характеристик
Скачок – единичное ступенчатое входное
Слайд 20Математическое описание САУ с помощью временных характеристик
Если скачок приложен к системе
где x(p) – скачок на входе
Слайд 21Математическое описание САУ с помощью временных характеристик
Импульс – мгновенное (кратковременное) изменение
Используется для имитации возмущающего воздействия на систему.
Слайд 22Математическое описание САУ с помощью частотных характеристик
Для определения динамических свойств системы
где Aвх – амплитуда входных колебаний;
ω – угловая частота колебаний;
t – время.
Слайд 23Математическое описание САУ с помощью частотных характеристик
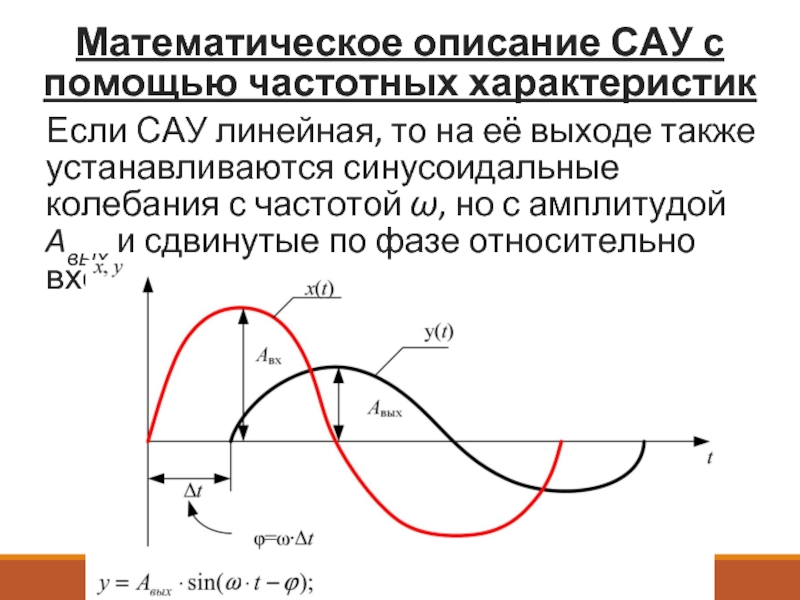
Если САУ линейная, то на
Слайд 24Математическое описание САУ с помощью частотных характеристик
Параметры Авых и φ зависят
Знак «минус» перед φ обусловлен тем, что в реальных системах выходное колебание отстаёт по фазе от входного.
Слайд 25Математическое описание САУ с помощью частотных характеристик
Запишем переменные x и y
Тогда:
Слайд 26Математическое описание САУ с помощью частотных характеристик
Поведение динамической системы характеризуют частотные
амплитудно-фазовая W(ω) (АФХ);
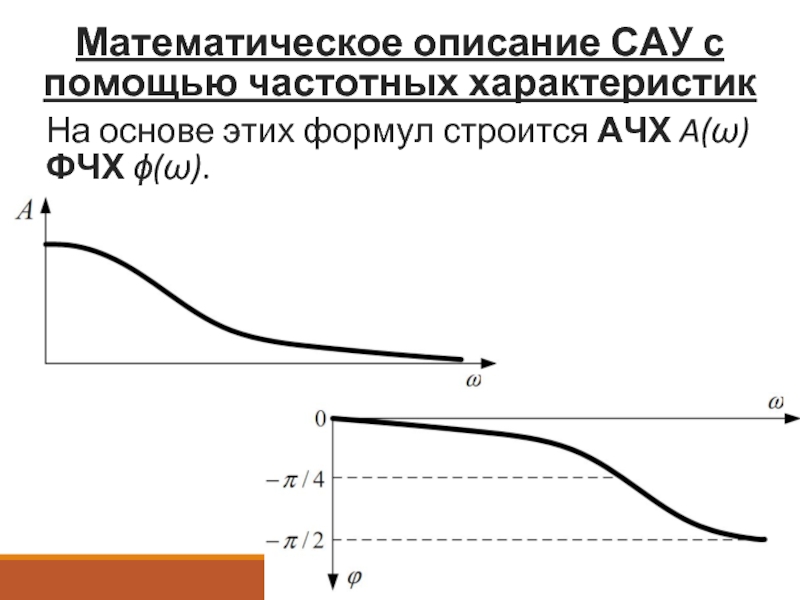
амплитудно-частотная A(ω) ( АЧХ );
фазово-частотная ϕ(ω) (ФЧХ).
Слайд 27Математическое описание САУ с помощью частотных характеристик
Пример Построить АФХ для динамической
Проводим замену p на jω
Слайд 28Математическое описание САУ с помощью частотных характеристик
Выделяем действительную Re (real) и
Изменяя частоты ω от 0 до n, строится АФХ.
Слайд 30Математическое описание САУ с помощью частотных характеристик
На основе этих формул строится
ФЧХ ϕ(ω).
Слайд 32Типовые динамические звенья САУ
При расчёте САУ ее разбивают на отдельные части
Эти блоки называют типовыми элементарными динамическими звеньями.
Слайд 33Типовые динамические звенья САУ
На практике используют 6 основных типовых элементарных динамических
усилительное;
апериодическое;
колебательное;
интегрирующее;
дифференцирующее;
чистого запаздывания.
Слайд 34Типовые динамические звенья САУ
1) Усилительное звено – передача сигнала без замедлений
k – коэффициент усиления (числовая величина).
Слайд 35Типовые динамические звенья САУ
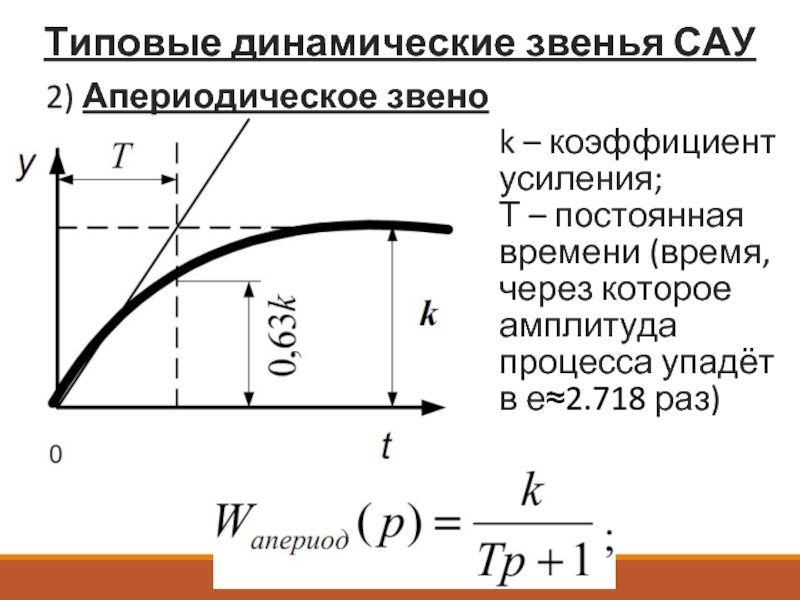
2) Апериодическое звено
k – коэффициент усиления;
Т – постоянная
Слайд 36Типовые динамические звенья САУ
3) Колебательное звено
T1 и T2 – постоянные времени
Слайд 37Типовые динамические звенья САУ
3) Колебательное звено
В зависимости от соотношения между T1
при T1 > 2T2 → корни вещественные;
при T1 = 2T2 → одинаковые вещественные корни, а переходные процессы протекают апериодически и звено не является колебательным;
при T1 < 2T2 → корни уравнения комплексные (колебательный процесс);
при T1 = 0 → незатухающие колебания.
Слайд 38Типовые динамические звенья САУ
4) Интегрирующее звено – выходная величина пропорциональна интегралу
Слайд 39Типовые динамические звенья САУ
5) Дифференцирующее звено
Идеальное дифференцирующее звено:
На практике невозможно,
Реальное дифференцирующее звено:







![Математическое описание САУ с помощью передаточных функцийПреобразование осуществляется с помощью прямого преобразования Лапласа L[x(t)]:где x(t)](/img/tmb/1/89501/cda39cd02266ce7fcb31aca2d165149c-800x.jpg)