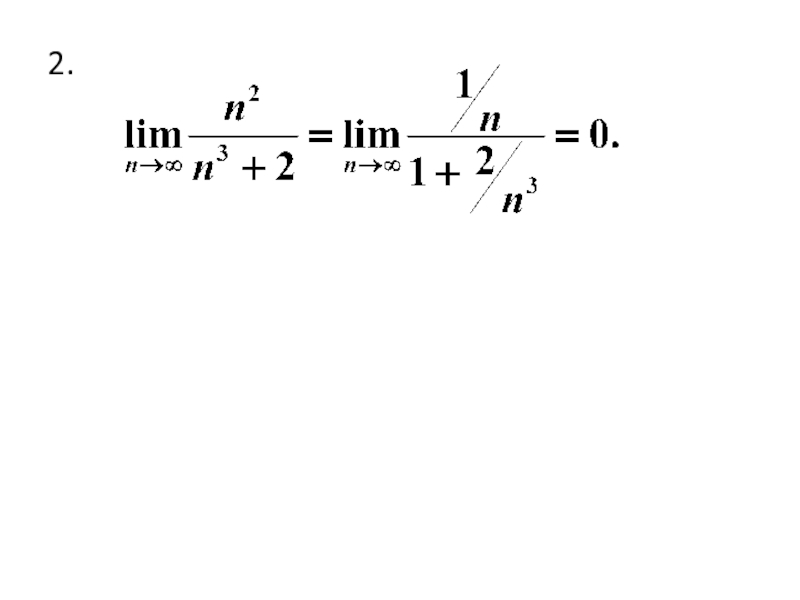- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые ряды презентация
Содержание
- 1. Числовые ряды
- 2. 1.1. Понятие числового ряда Пусть
- 3. Ряд (1) считается заданным, если известен
- 4. Если для последовательности частичных сумм ряда
- 5. Пример Ряд 0+0+0+...+0+... сходится,
- 6. Свойства рядов 1. Если к ряду (1)
- 7. 3. Если ряды
- 8. Замечания 1. Из свойства 3 вытекает, что
- 9. Ряд называется n-м остатком ряда (1).
- 10. Из свойства 1 также следует ,
- 11. Необходимый признак сходимости ряда Если ряд
- 12. Достаточный признак расходимости ряда Если
- 13. Пример Исследовать сходимость ряда Решение. 1. Найдем предел общего члена ряда:
- 14. 2.
- 15. §2. Достаточные признаки сходимости рядов с положительными членами
- 16. Первый признак сравнения Если для членов рядов
- 17. Второй признак сравнения Пусть
- 18. Ряды, используемые при применении признаков сравнения 1.
- 19. 2. Ряд, составленный из членов геометричес-кой прогрессии,
- 20. Обобщенный гармонический ряд
- 21. Пример Ряд
- 22. Признак Даламбера Пусть
- 23. Если то ряд может
- 24. Вспомогательные сведения
- 25. Пример Записать общий член ряда, 2 первых
- 26. Подставляя в формулу общего члена ряда вместо
- 27. 2. Используя признак Даламбера исследовать ряд на
- 28. Найдем По признаку Даламбера ряд сходится.
- 29. §3. ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ
- 30. 3.1. Знакочередующиеся ряды Ряд вида
- 31. Признак Лейбница Пусть дан знакочередующийся ряд (4).
- 32. Замечания 1. Ряды вида (4), для
- 33. Отброшенный ряд (остаток) представляет собой также знакочередующийся
- 34. Абсолютная сходимость Знакочередующийся ряд называется абсолютно сходящимся,
- 35. Пример Исследовать на сходимость ряд
- 36. Выясним, сходится ли он условно. Используем признак
- 37. Таким образом, ряд сходится условно.
1.1. Понятие числового ряда Пусть – числовая последовательность.
Слайд 21.1. Понятие числового ряда
Пусть
– числовая последовательность.
Выражение вида
называется числовым рядом,
числа – члены ряда,
– n-й или общий член ряда.
Выражение вида
называется числовым рядом,
числа – члены ряда,
– n-й или общий член ряда.
Слайд 3 Ряд (1) считается заданным, если известен общий член ряда, выраженный
как функция его номера n:
Сумма конечного числа n первых членов ряда (1)
называется n-й частичной суммой. Таким образом,
Сумма конечного числа n первых членов ряда (1)
называется n-й частичной суммой. Таким образом,
Слайд 4 Если для последовательности частичных сумм ряда (1) существует конечный предел
то ряд (1) называется сходящимся, а число – S – суммой данного ряда ( ).
Если не существует или равен бесконечности, то ряд (1) называется расходящимся. Такой ряд суммы не имеет.
Слайд 5Пример
Ряд 0+0+0+...+0+... сходится, его сумма S=0.
Ряд 1+1+1+...+1+...
расходится, так как предел
Ряд 1-1+1-1+... расходится, так как последовательность частичных сумм
предела не имеет.
Ряд 1-1+1-1+... расходится, так как последовательность частичных сумм
предела не имеет.
Слайд 6Свойства рядов
1. Если к ряду (1) прибавить или отбросить конечное число
его членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно.
2. Если ряд (1) сходится и его сумма равна S, а λ – некоторое число, то ряд
сходится и его сумма равна λS.
2. Если ряд (1) сходится и его сумма равна S, а λ – некоторое число, то ряд
сходится и его сумма равна λS.
Слайд 8Замечания
1. Из свойства 3 вытекает, что сумма (разность) сходящегося и расходящегося
рядов есть расходящийся ряд.
2. Сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.
2. Сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.
Слайд 9 Ряд
называется n-м остатком ряда (1). Он получается из ряда (1) отбрасыванием
n первых его членов.
Ряд (1) получается из остатка добавлением конечного числа членов. Поэтому согласно свойству 1, ряд (1) и его остаток одновременно сходятся или расходятся.
Ряд (1) получается из остатка добавлением конечного числа членов. Поэтому согласно свойству 1, ряд (1) и его остаток одновременно сходятся или расходятся.
Слайд 10
Из свойства 1 также следует , что если ряд (1) сходится,
то его остаток
стремится к нулю при
стремится к нулю при
Слайд 11Необходимый признак сходимости ряда
Если ряд
сходится, то общий член ряда стремится к нулю при , т.е.
Слайд 16Первый признак сравнения
Если для членов рядов
справедливо неравенство
для всех , то
из сходимости ряда (3) следует сходимость ряда (2);
из расходимости ряда (2) следует расходимость ряда (3).
для всех , то
из сходимости ряда (3) следует сходимость ряда (2);
из расходимости ряда (2) следует расходимость ряда (3).
Слайд 17Второй признак сравнения
Пусть
и
– ряды с положительными членами, причем существует конечный и отличный от нуля предел
Тогда ряды
сходятся или расходятся одновременно.
– ряды с положительными членами, причем существует конечный и отличный от нуля предел
Тогда ряды
сходятся или расходятся одновременно.
Слайд 18Ряды, используемые при применении признаков сравнения
1. Гармонический ряд –
расходящийся ряд.
Слайд 192. Ряд, составленный из членов геометричес-кой прогрессии,
при
сходится и его сумма равна
при расходится.
при расходится.
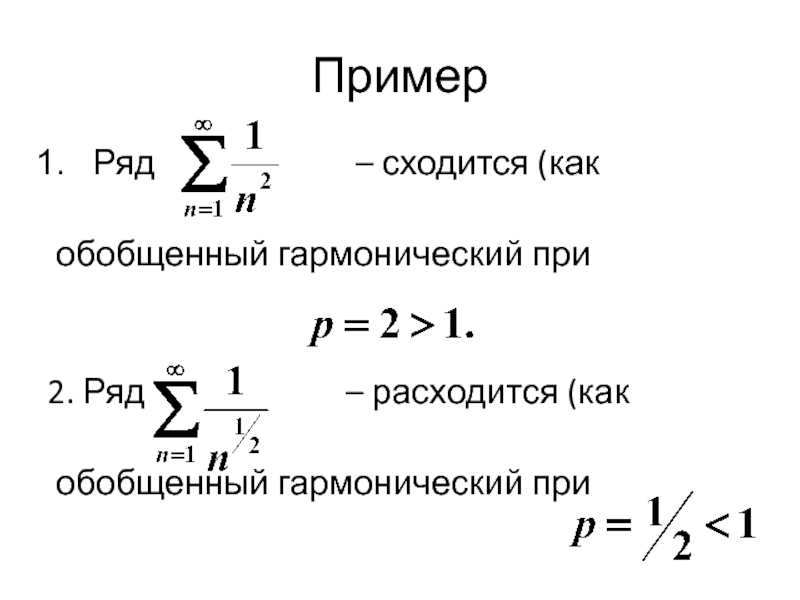
Слайд 21Пример
Ряд
– сходится (как
обобщенный гармонический при
2. Ряд – расходится (как
обобщенный гармонический при
обобщенный гармонический при
2. Ряд – расходится (как
обобщенный гармонический при
Слайд 22Признак Даламбера
Пусть
– ряд с положительными
членами, и существует конечный предел
Тогда, если , то данный ряд сходится;
если же , то – расходится.
членами, и существует конечный предел
Тогда, если , то данный ряд сходится;
если же , то – расходится.
Слайд 23 Если
то ряд может сходиться или расходиться.
Ряд требуется исследовать
с помощью других признаков сходимости.
Слайд 25Пример
Записать общий член ряда, 2 первых члена ряда и (n+1 )-й
член ряда.
Решение. Формула общего члена ряда:
Решение. Формула общего члена ряда:
Слайд 272. Используя признак Даламбера исследовать ряд на сходимость.
Решение.
общий член ряда:
(n+1)-й
член ряда:
Слайд 31Признак Лейбница
Пусть дан знакочередующийся ряд (4). Если выполнены два условия
последовательность
абсолютных величин членов ряда монотонно убывает:
2) общий член ряда стремится к нулю при
:
то ряд сходится. При этом сумма ряда удовлетворяет неравенствам
2) общий член ряда стремится к нулю при
:
то ряд сходится. При этом сумма ряда удовлетворяет неравенствам
Слайд 32Замечания
1. Ряды вида (4), для которых выполняются условия теоремы Лейбница, называются
лейбницевскими (или рядами Лейбница).
2. Соотношение (5) позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой
2. Соотношение (5) позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой
Слайд 33Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд
сумма которого по
модулю меньше первого члена этого ряда, т. е.
Поэтому ошибка меньше модуля первого из отброшенных членов.
Поэтому ошибка меньше модуля первого из отброшенных членов.
Слайд 34Абсолютная сходимость
Знакочередующийся ряд называется абсолютно сходящимся, если ряд, составленный из модулей
его членов, сходится. В этом случае сходится и сам знакочередующийся ряд.
Знакочередующийся ряд называется условно сходящимся, если ряд из модулей его членов расходится, а сам знакочередующийся ряд сходится.
Знакочередующийся ряд называется условно сходящимся, если ряд из модулей его членов расходится, а сам знакочередующийся ряд сходится.
Слайд 35Пример
Исследовать на сходимость ряд
Решение. Исследуем на сходимость ряд из модулей:
Это обобщенный
гармонический ряд (p=1/3), поэтому ряд расходится.
Следовательно абсолютной сходимости нет.
Следовательно абсолютной сходимости нет.
Слайд 36Выясним, сходится ли он условно. Используем признак Лейбница:
последовательность абсолютных величин членов
ряда монотонно убывает:
общий член ряда стремится к нулю:
общий член ряда стремится к нулю:
