Zemkoho, Professor Jörg Fliege
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Solution methods for bilevel optimization презентация
Содержание
- 1. Solution methods for bilevel optimization
- 2. Overview Definition and general form of a
- 3. Stackelberg Game (Bilevel problem) Players:
- 4. Example Taxation of a factory Leader –
- 5. General structure of a Bilevel problem
- 6. Important Sets
- 7. Solution methods Vertex enumeration in
- 8. Concept of KKT conditions
- 9. Value function reformulation
- 10. KKT for value function reformulation
- 11. Assumptions
- 12. KKT-type optimality conditions for Bilevel
- 13. Further Assumptions (for simpler version)
- 14. Simpler version
- 15. NCP-Functions Define Give a reason (non-differentiability of constraints) Fischer-Burmeister
- 16. Simpler version in the form of the system of equations
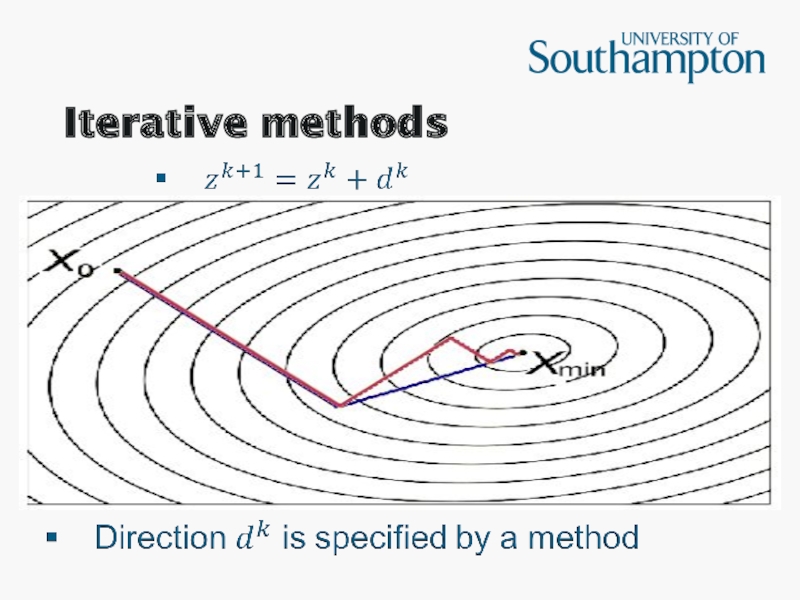
- 17. Iterative methods
- 18. For Bilevel case
- 19. Newton method Define Explain that
- 20. Pseudo inverse
- 21. Newton method with pseudo inverse
- 22. Gauss-Newton method Define Mention the wrong formulation Refer to pseudo-inverse Newton
- 23. Gauss-Newton method
- 24. Convergence of Newton and Gauss-Newton
- 25. Levenberg-Marquardt method
- 26. Numerical results
- 27. Plans for further work
- 28. Plans for further work 6.
- 31. References
- 32. References
Слайд 1Solution Methods for Bilevel Optimization
Andrey Tin
A.Tin@soton.ac.uk
School of Mathematics
Supervisors: Dr Alain B.
Слайд 2Overview
Definition and general form of a bilevel problem
Discuss optimality (KKT-type) conditions
Reformulate
general bilevel problem as a system of equations
Consider iterative (descent direction) methods applicable to solve this reformulation
Look at the numerical results of using Levenberg-Marquardt method
Consider iterative (descent direction) methods applicable to solve this reformulation
Look at the numerical results of using Levenberg-Marquardt method
Слайд 3Stackelberg Game (Bilevel problem)
Players: the Leader and the Follower
The Leader is
first to make a decision
Follower reacts optimally to Leader’s decision
The payoff for the Leader depends on the follower’s reaction
Follower reacts optimally to Leader’s decision
The payoff for the Leader depends on the follower’s reaction
Слайд 4Example
Taxation of a factory
Leader – government
Objectives: maximize profit and minimize pollution
Follower
– factory owner
Objectives: maximize profit
Objectives: maximize profit
Слайд 7Solution methods
Vertex enumeration in the context of Simplex method
Kuhn-Tucker approach
Penalty approach
Extract
gradient information from a lower objective function to compute directional derivatives of an upper objective function
Слайд 19Newton method
Define
Explain that we are dealing with non-square system
Suggest pseudo inverse
Newton
Слайд 24Convergence of Newton and Gauss-Newton
Talk about starting point condition
Interest for future
analysis
Слайд 28Plans for further work
6. Construct the own code for Levenberg-Marquardt method
in the context of solving bilevel problems within defined reformulation.
7. Search for good starting point techniques for our problem. 8. Do the numerical calculations for the harder reformulation defined .
9. Code Newton method with pseudo-inverse.
10. Solve the problem assuming strict complementarity
11. Look at other solution methods.
7. Search for good starting point techniques for our problem. 8. Do the numerical calculations for the harder reformulation defined .
9. Code Newton method with pseudo-inverse.
10. Solve the problem assuming strict complementarity
11. Look at other solution methods.