- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранник пирамида презентация
Содержание
- 1. Многогранник пирамида
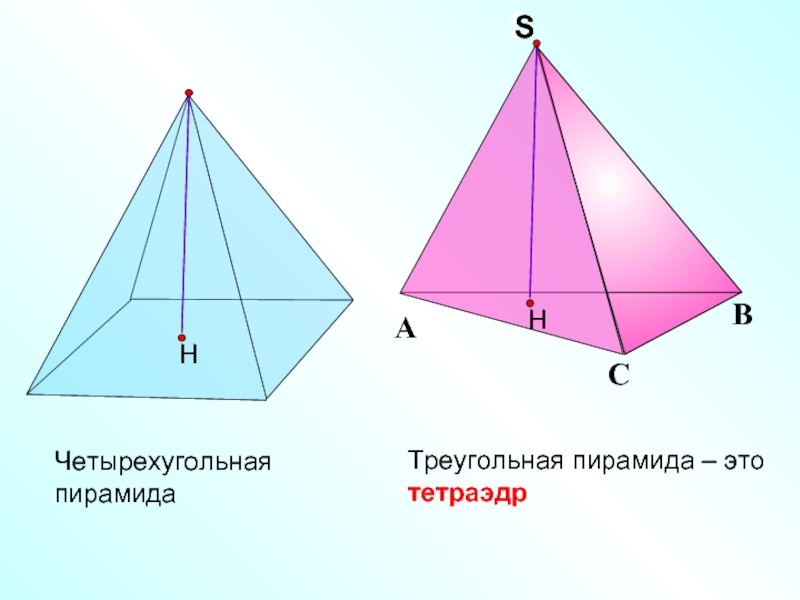
- 3. Треугольная пирамида – это тетраэдр Четырехугольная пирамида
- 4. Пятиугольная пирамида
- 5. Пирамида называется правильной,
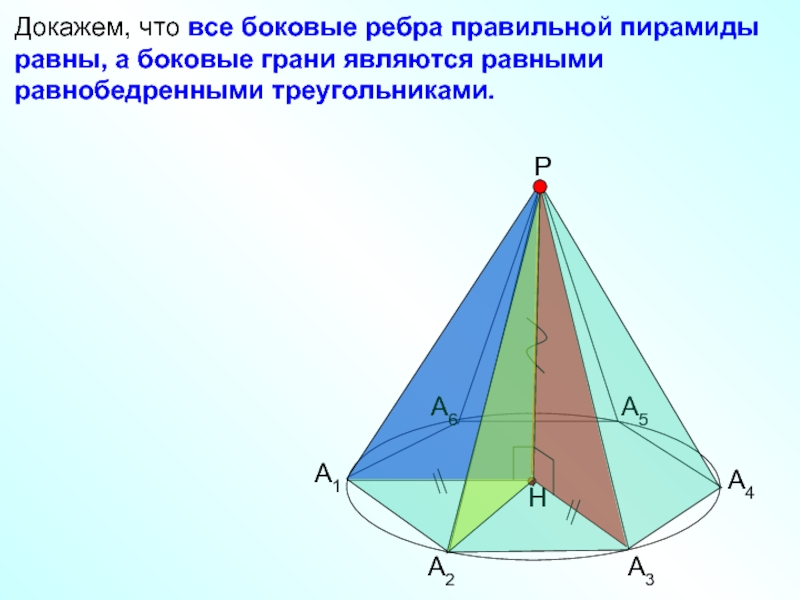
- 6. Докажем, что все боковые
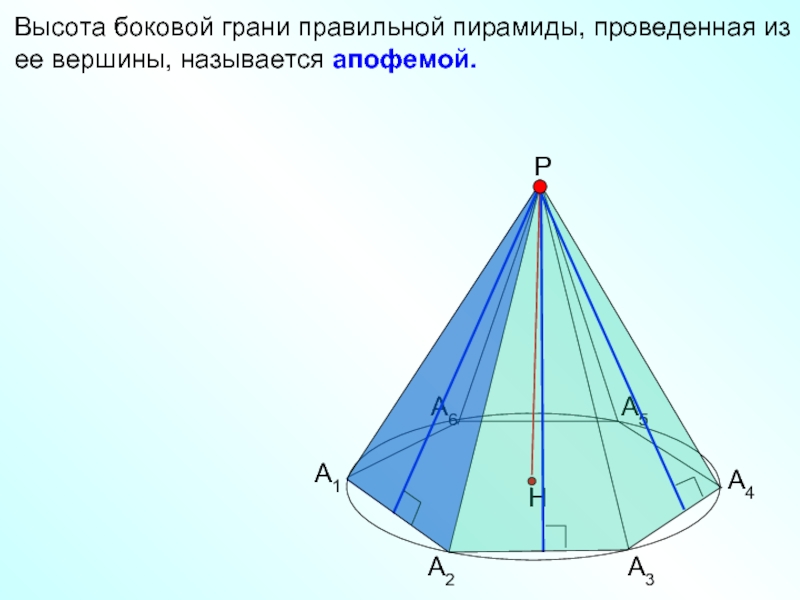
- 7. Высота боковой грани правильной
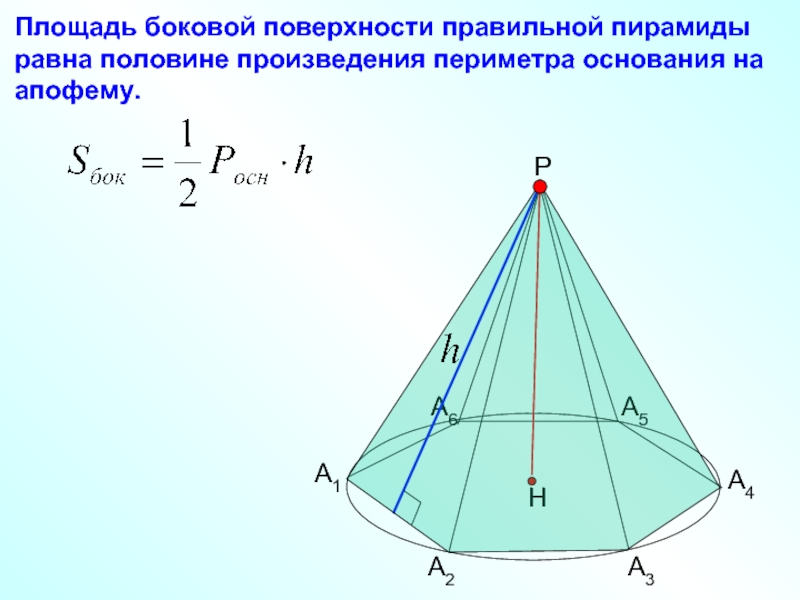
- 8. Площадь боковой поверхности правильной
- 9. С А В Н №
- 10. С В А D
- 11. С В А D
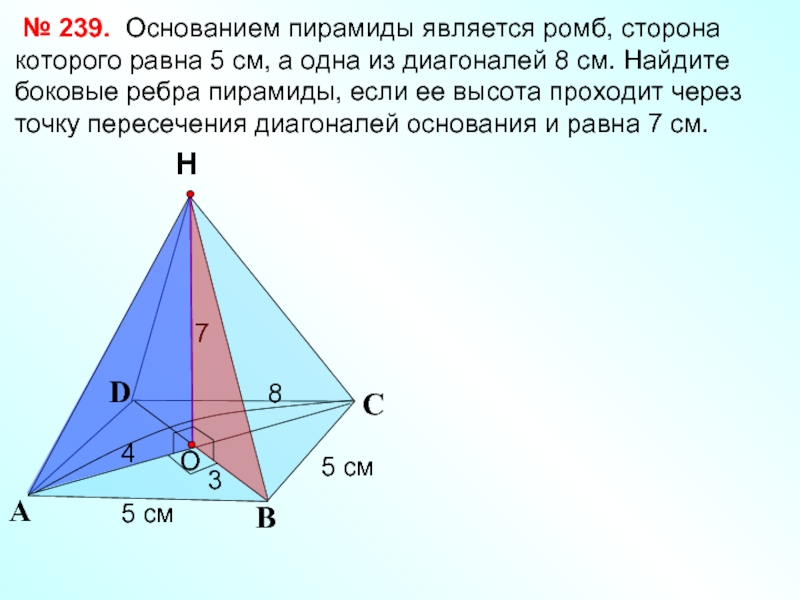
- 13. D Н
- 16. А
- 18. - Если двугранные углы при основании
- 20. № 249.
- 21. А1 А2
- 22. № 250. Основанием пирамиды является равнобедренный
- 23. № 250. Для тупоугольного треугольника центр
- 24. А № 251. Основанием пирамиды DABC
- 25. № 251. Для прямоугольного треугольника
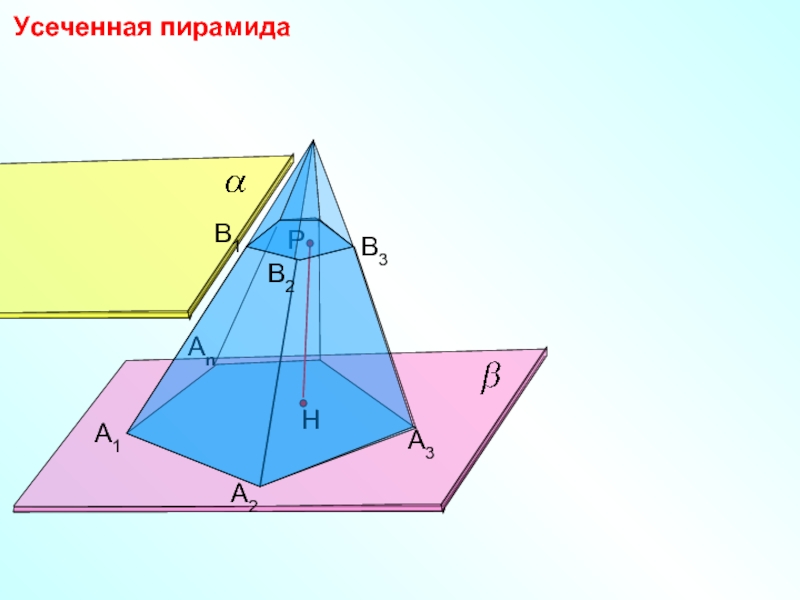
- 26. А1 А2 Аn А3 Усеченная пирамида
А1 А2 Аn Р А3 Многогранник, составленный из n-угольника А1А2…Аn n треугольников, называется пирамидой. Вершина Перпендикуляр, проведенный из вершины
Слайд 2
А1
А2
Аn
Р
А3
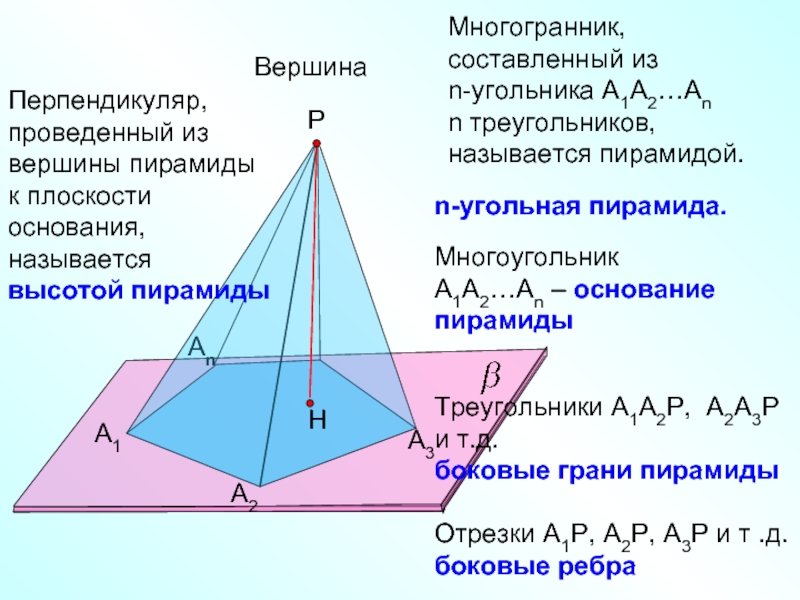
Многогранник, составленный из
n-угольника А1А2…Аn
n треугольников, называется пирамидой.
Вершина
Перпендикуляр, проведенный из
вершины пирамиды к плоскости основания, называется высотой пирамиды
n-угольная пирамида.
Многоугольник
А1А2…Аn – основание пирамиды
Треугольники А1А2Р, А2А3Р и т.д.
боковые грани пирамиды
Отрезки А1Р, А2Р, А3Р и т .д.
боковые ребра
Слайд 5
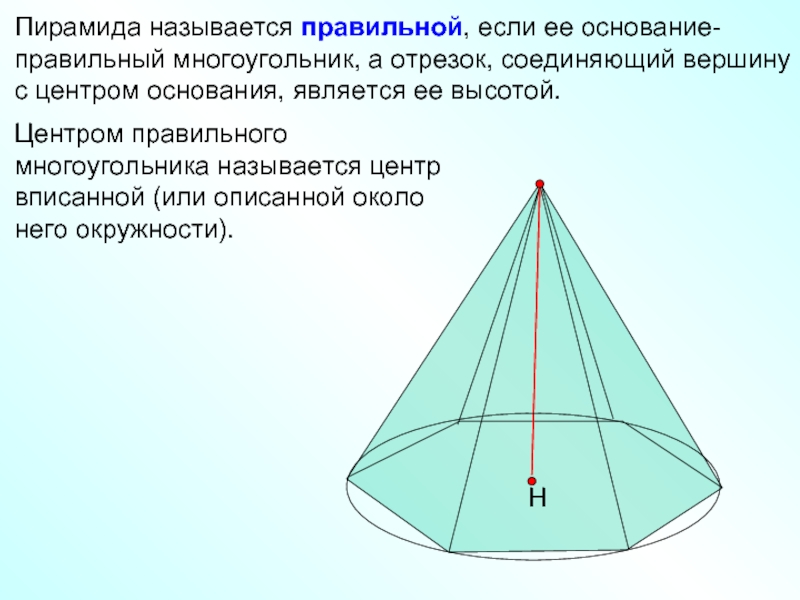
Пирамида называется правильной, если ее основание- правильный многоугольник, а отрезок, соединяющий
вершину с центром основания, является ее высотой.
Центром правильного многоугольника называется центр вписанной (или описанной около него окружности).
Слайд 6
Докажем, что все боковые ребра правильной пирамиды равны, а боковые грани
являются равными равнобедренными треугольниками.
А1
А2
А3
А4
А5
А6
Р
Слайд 7
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
А1
А2
А3
А4
А5
А6
Р
Слайд 8
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на
апофему.
А1
А2
А3
А4
А5
А6
Р
Слайд 9
С
А
В
Н
№ 239. Основанием пирамиды является ромб, сторона которого равна 5
см, а одна из диагоналей 8 см. Найдите боковые ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна 7 см.
O
D
5 см
5 см
7
4
3
Слайд 10
С
В
А
D
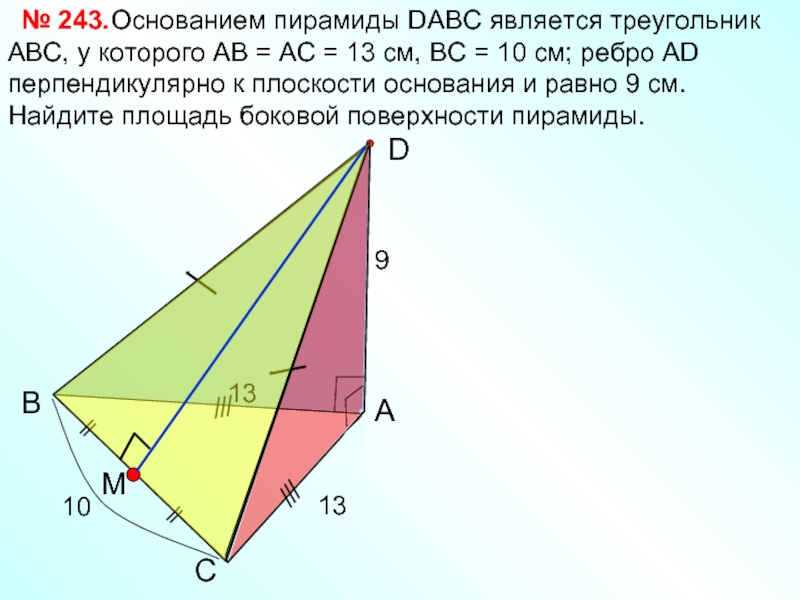
Основанием пирамиды DАВС является
треугольник АВС, у которого АВ = АС = 13 см, ВС = 10 см; ребро АD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.
№ 243.
13
9
10
13
Слайд 11
С
В
А
D
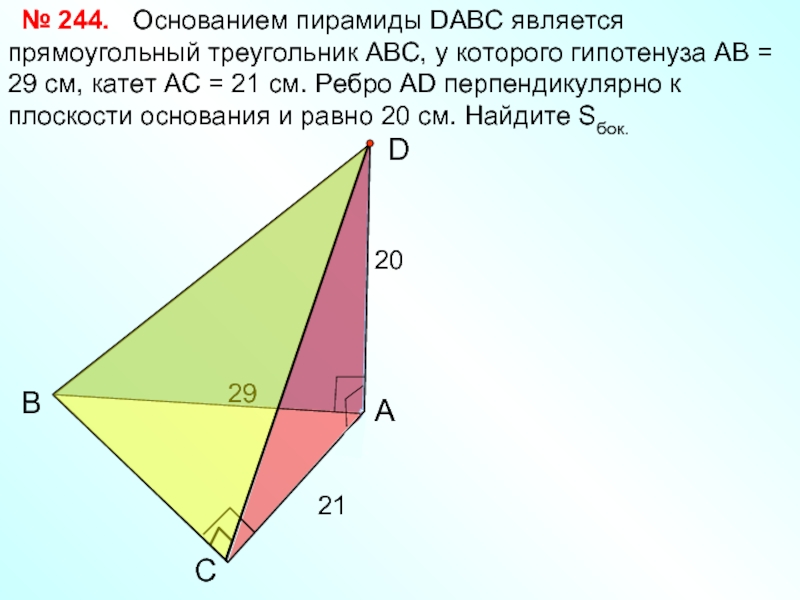
Основанием пирамиды
DАВС является прямоугольный треугольник АВС, у которого гипотенуза АВ = 29 см, катет АС = 21 см. Ребро АD перпендикулярно к плоскости основания и равно 20 см. Найдите Sбок.
№ 244.
21
20
29
Слайд 12
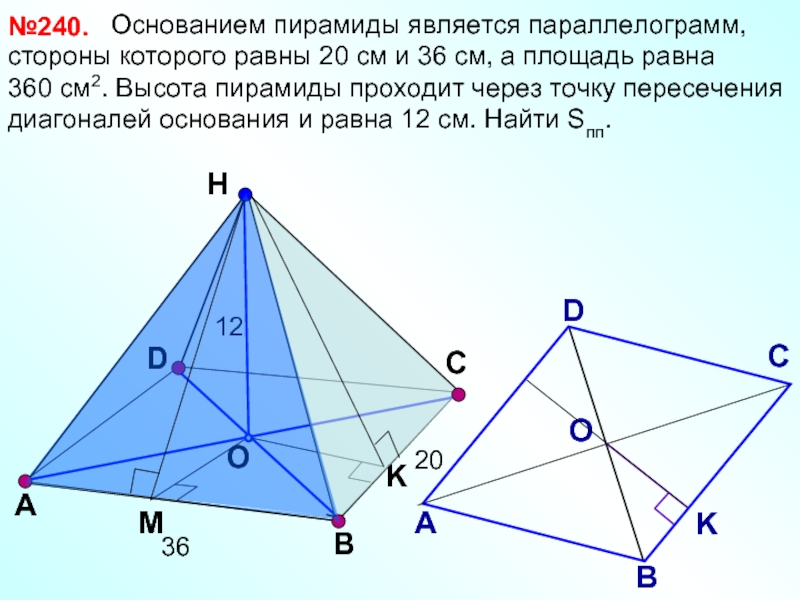
Основанием пирамиды является параллелограмм,
стороны которого равны 20 см и 36 см, а площадь равна
360 см2. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найти Sпп.
360 см2. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найти Sпп.
D
Н
O
А
B
№240.
С
20
36
12
Слайд 13
D
Н
O
А
B
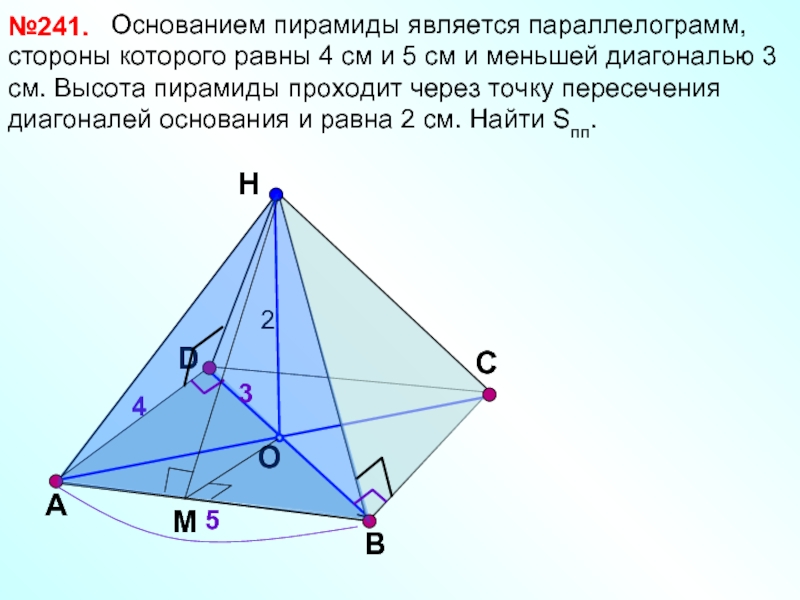
№241.
С
4
5
2
3
Основанием пирамиды является параллелограмм,
стороны которого равны 4 см и 5 см и меньшей диагональю 3 см. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 см. Найти Sпп.
Слайд 14
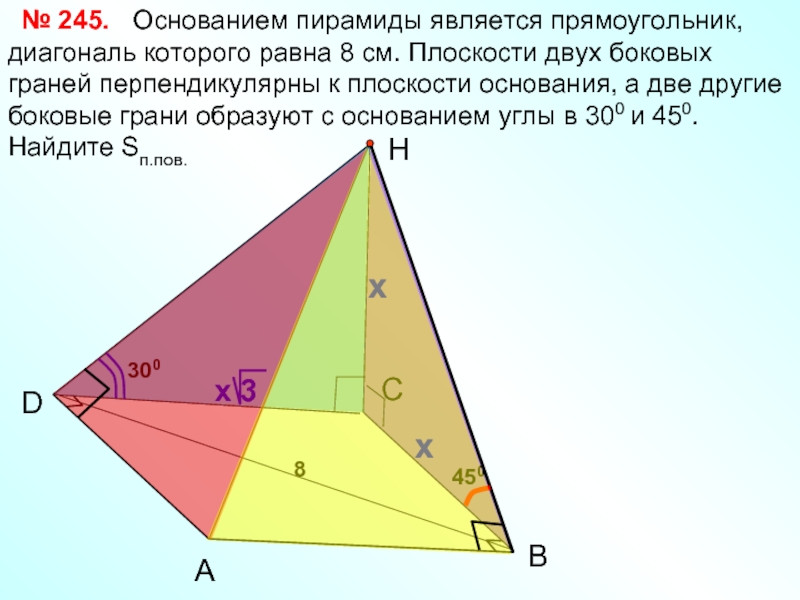
Основанием пирамиды
является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 300 и 450. Найдите Sп.пов.
А
D
Н
№ 245.
x
В
450
8
С
300
x
Слайд 15
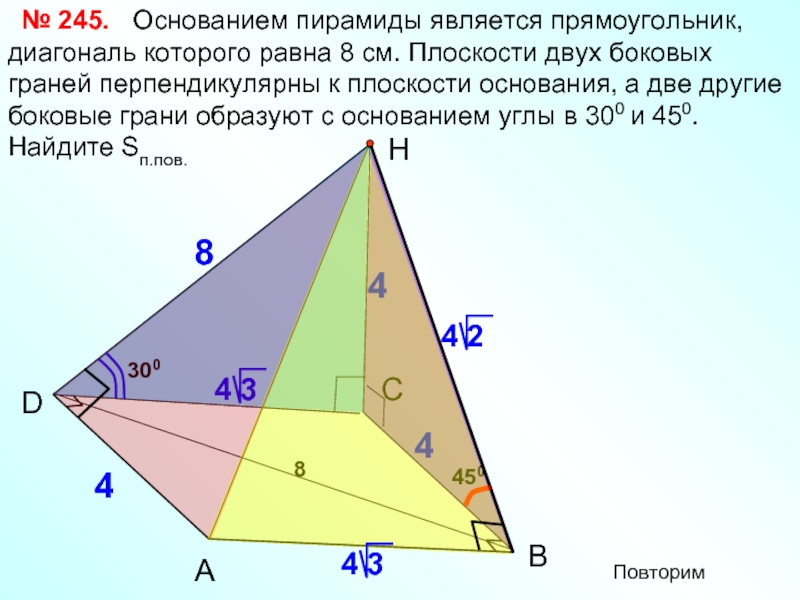
Основанием пирамиды
является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 300 и 450. Найдите Sп.пов.
А
D
Н
№ 245.
4
В
450
8
С
300
4
4
8
Повторим
Слайд 16
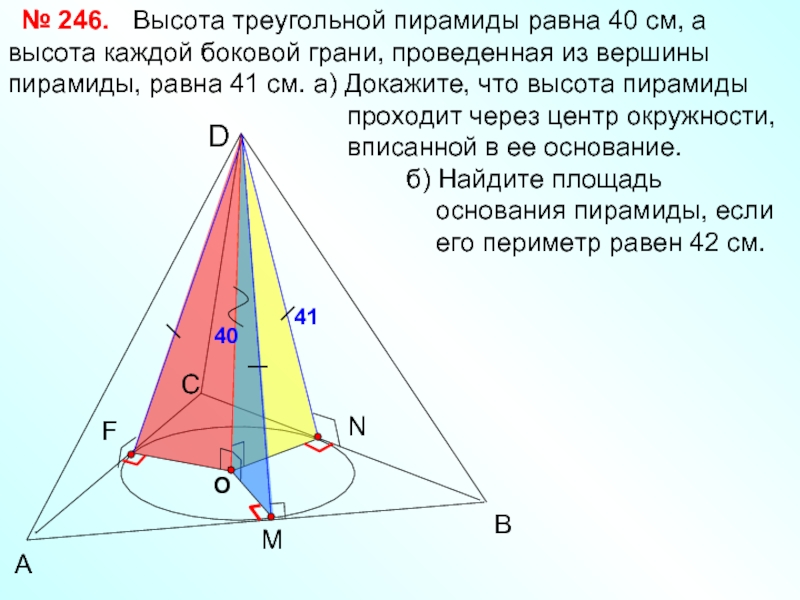
А
В
С
D
Высота треугольной
пирамиды равна 40 см, а высота каждой боковой грани, проведенная из вершины пирамиды, равна 41 см. а) Докажите, что высота пирамиды
проходит через центр окружности,
вписанной в ее основание.
б) Найдите площадь
основания пирамиды, если
его периметр равен 42 см.
проходит через центр окружности,
вписанной в ее основание.
б) Найдите площадь
основания пирамиды, если
его периметр равен 42 см.
№ 246.
Слайд 17
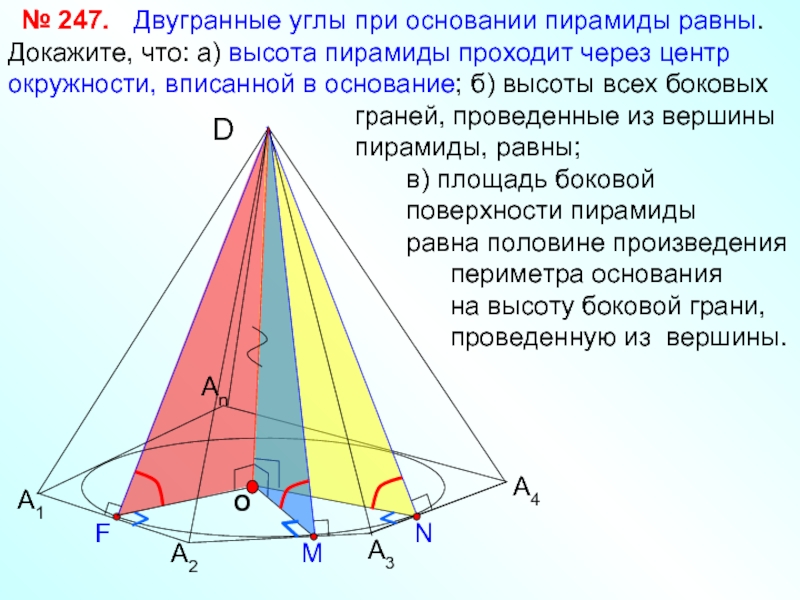
Двугранные углы
при основании пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр окружности, вписанной в основание; б) высоты всех боковых
граней, проведенные из вершины
пирамиды, равны;
в) площадь боковой
поверхности пирамиды
равна половине произведения
периметра основания
на высоту боковой грани,
проведенную из вершины.
граней, проведенные из вершины
пирамиды, равны;
в) площадь боковой
поверхности пирамиды
равна половине произведения
периметра основания
на высоту боковой грани,
проведенную из вершины.
№ 247.
А1
Аn
D
А2
А3
А4
Слайд 18
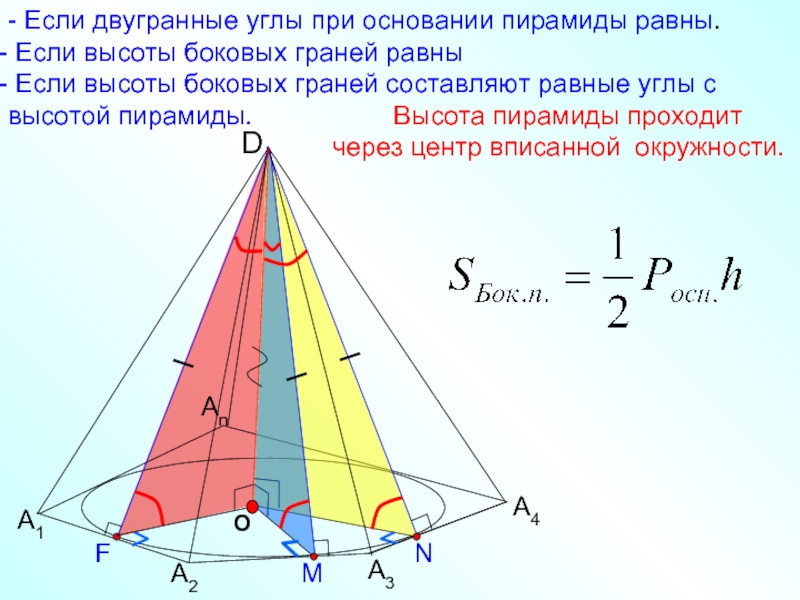
- Если двугранные углы при основании пирамиды равны.
Если высоты
боковых граней равны
Если высоты боковых граней составляют равные углы с высотой пирамиды. Высота пирамиды проходит
через центр вписанной окружности.
Если высоты боковых граней составляют равные углы с высотой пирамиды. Высота пирамиды проходит
через центр вписанной окружности.
А1
Аn
D
А2
А3
А4
Слайд 19
А
В
С
D
Основанием пирамиды
является треугольник с сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь
боковой поверхности пирамиды.
боковой поверхности пирамиды.
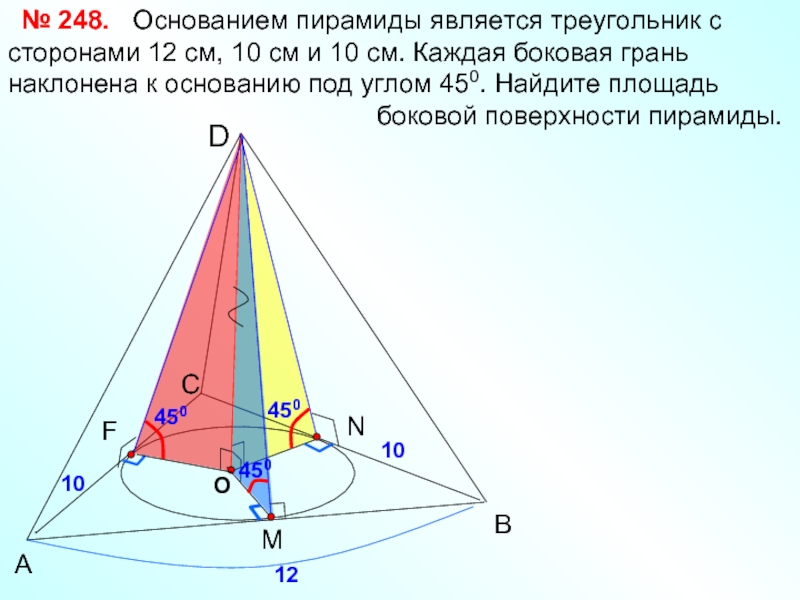
№ 248.
12
10
10
Слайд 20
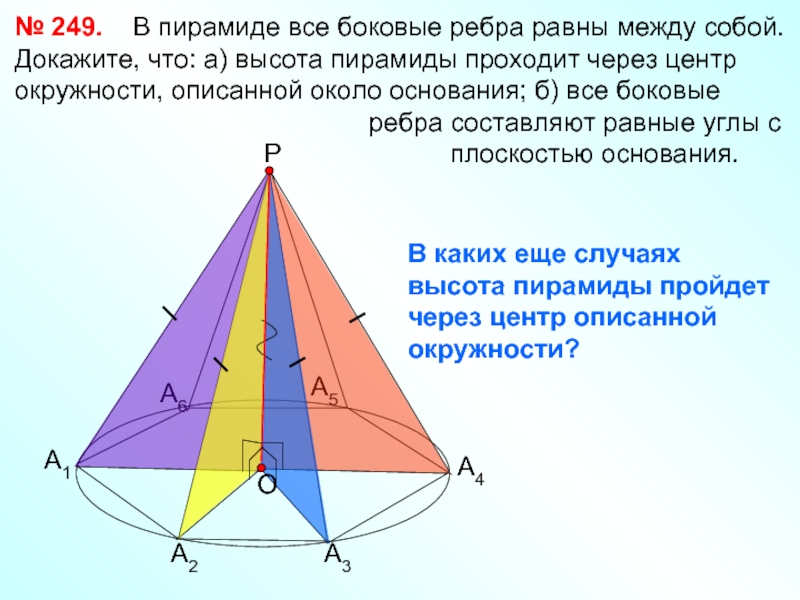
№ 249. В пирамиде все боковые ребра равны между собой.
Докажите, что: а) высота пирамиды проходит через центр окружности, описанной около основания; б) все боковые
ребра составляют равные углы с
плоскостью основания.
ребра составляют равные углы с
плоскостью основания.
А1
А2
А3
А4
А5
А6
Р
В каких еще случаях высота пирамиды пройдет через центр описанной окружности?
Слайд 21
А1
А2
А3
А4
А5
А6
Р
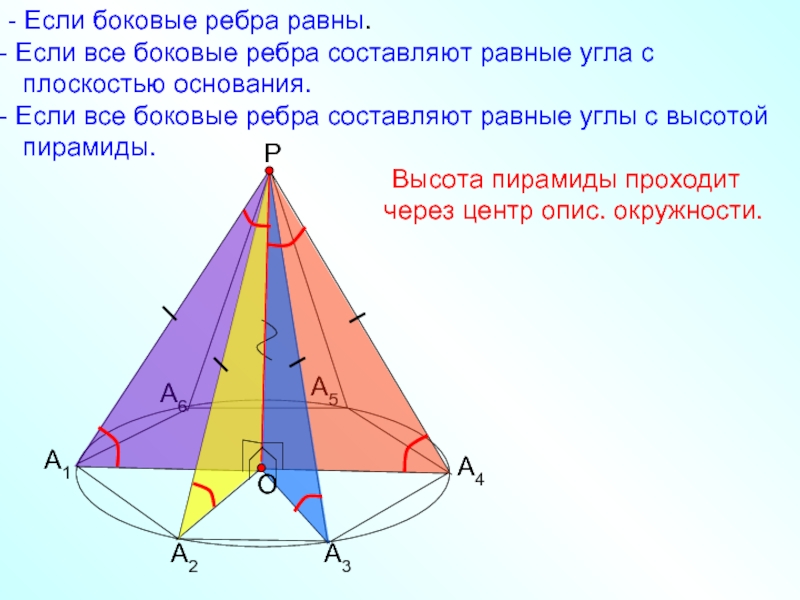
- Если боковые ребра равны.
Если все боковые ребра составляют
равные угла с
плоскостью основания.
Если все боковые ребра составляют равные углы с высотой
пирамиды.
Высота пирамиды проходит
через центр опис. окружности.
плоскостью основания.
Если все боковые ребра составляют равные углы с высотой
пирамиды.
Высота пирамиды проходит
через центр опис. окружности.
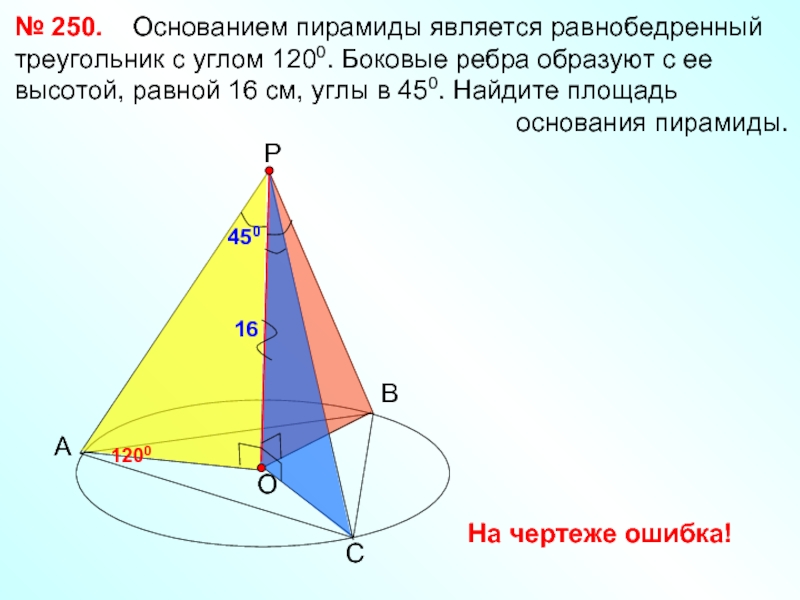
Слайд 22№ 250. Основанием пирамиды является равнобедренный треугольник с углом 1200.
Боковые ребра образуют с ее высотой, равной 16 см, углы в 450. Найдите площадь
основания пирамиды.
основания пирамиды.
А
В
С
Р
1200
450
16
На чертеже ошибка!
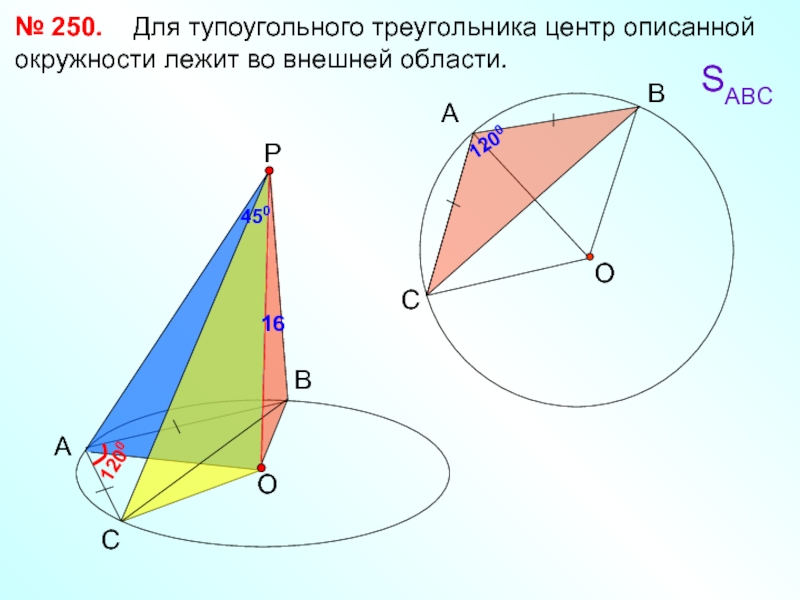
Слайд 23№ 250. Для тупоугольного треугольника центр описанной окружности лежит во
внешней области.
А
В
С
Р
1200
SАВС
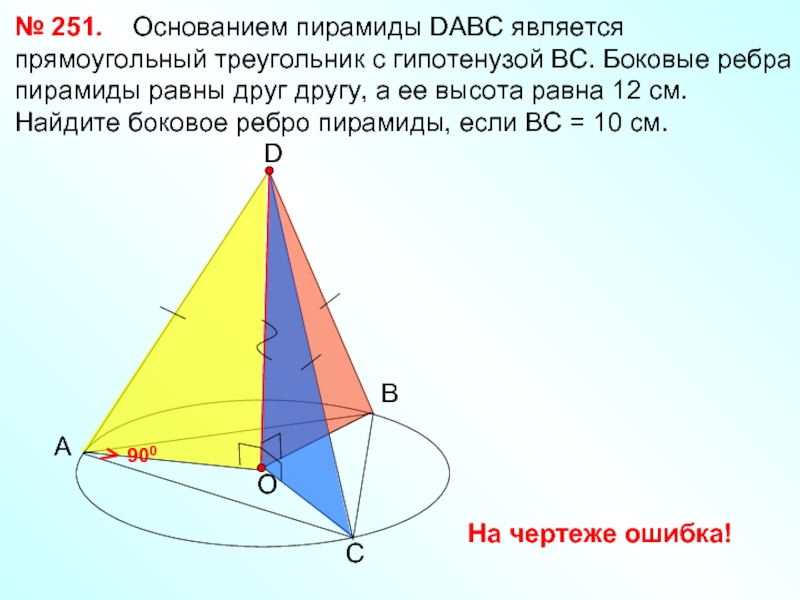
Слайд 24А
№ 251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой
ВС. Боковые ребра пирамиды равны друг другу, а ее высота равна 12 см. Найдите боковое ребро пирамиды, если ВС = 10 см.
В
С
D
900
На чертеже ошибка!
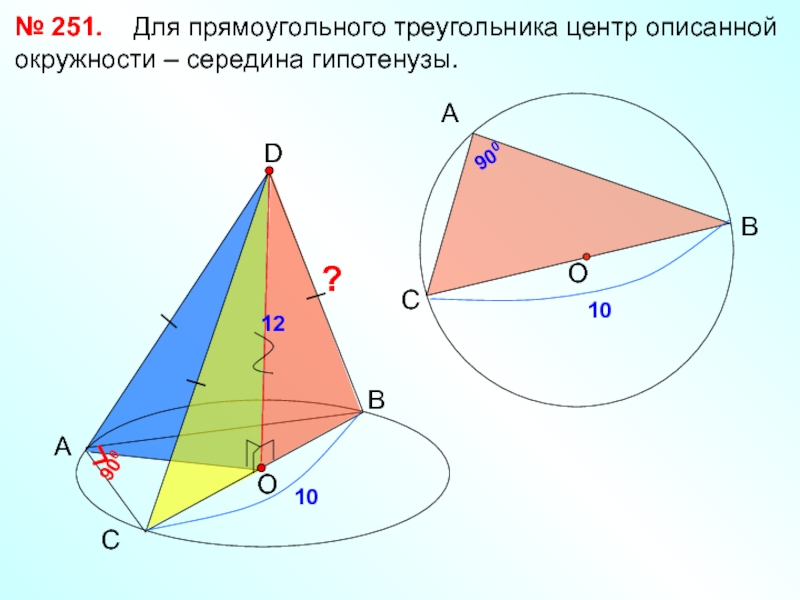
Слайд 25
№ 251. Для прямоугольного треугольника центр описанной окружности – середина
гипотенузы.
А
В
С
D
900
10
