- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случайные величины, законы их распределения и числовые характеристики презентация
Содержание
- 1. Случайные величины, законы их распределения и числовые характеристики
- 2. Основные вопросы: Понятие случайной величины. Закон распределения случайной величины. Числовые характеристики дискретных случайных величин.
- 3. Определение Случайной величиной называется переменная величина, которая
- 4. Определение Дискретной случайной величиной называется такая величина,
- 5. Определение Непрерывной случайной величиной называется такая величина,
- 6. ЗАКОН РАСПРЕДЕЛЕНИЯ Законом распределения
- 7. Рассмотрим дискретную случайную величину X с возможными
- 8. Ряд распределения случайной величины X имеет следующий
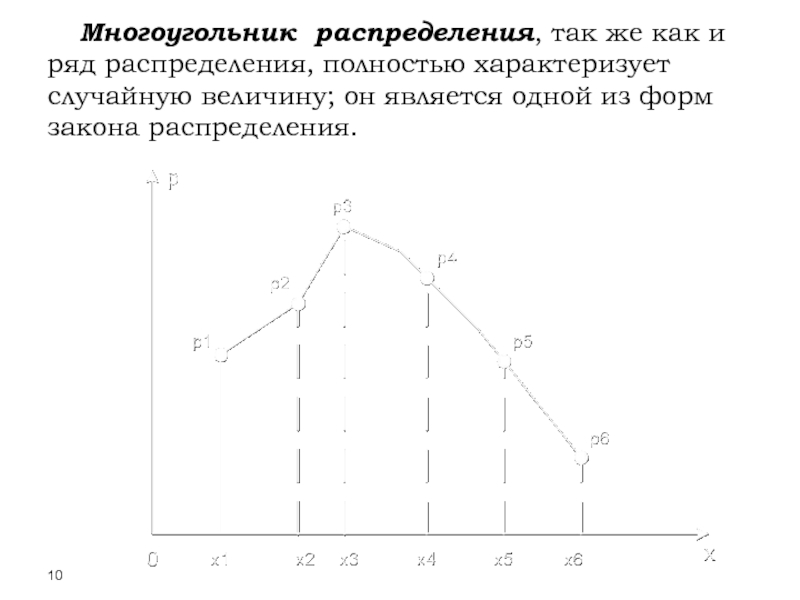
- 10. Многоугольник распределения, так же как и ряд
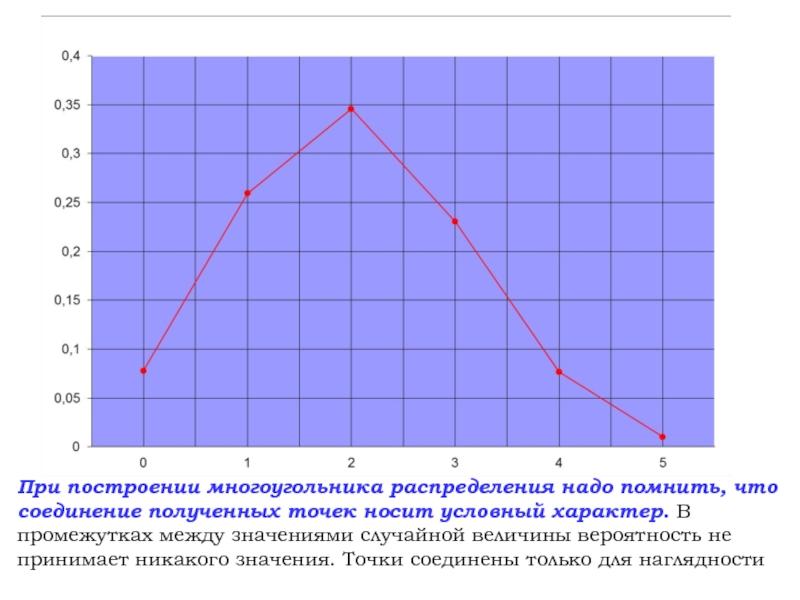
- 13. При построении многоугольника распределения надо помнить, что
- 14. Биноминальное распределение Если производится
- 17. Числовые характеристики дискретных случайных величин
- 18. Математическое
- 20. Свойства математического ожидания: Математическое ожидание постоянной величины
- 21. 3. Математическое ожидание произведения двух независимых случайных
- 22. Пусть производится п независимых испытаний, вероятность
- 23. Дисперсия Дисперсией (рассеиванием) D(X) дискретной случайной величины
- 25. Теорема Дисперсия равна разности между математическим ожиданием
- 26. Свойства дисперсии: Дисперсия постоянной величины равна нулю.
- 27. Свойства дисперсии: Дисперсия суммы двух независимых случайных
- 28. Теорема Дисперсия числа появления события А в
- 29. Среднее квадратическое отклонение Средним квадратическим отклонением случайной
- 30. Теорема Среднее квадратичное отклонение суммы конечного числа
- 32. Домашнее задание: 1. Письменный Д.Т. Конспект лекций
- 33. Задачи
Слайд 2Основные вопросы:
Понятие случайной величины. Закон распределения случайной величины.
Числовые характеристики дискретных случайных
Слайд 3Определение
Случайной величиной называется переменная величина, которая в результате опыта может принимать
Пример
Случайными величинами являются: температура больного в некоторое наугад выбранное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента.
Слайд 4Определение
Дискретной случайной величиной называется такая величина, которая в результате опыта может
Это множество может быть как конечным, так и бесконечным.
Например, число посетителей аптеки в течение дня, количество яблок на дереве.
Слайд 5Определение
Непрерывной случайной величиной называется такая величина, которая может принимать любые значения
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Например: температура больного в фиксированное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента
Слайд 6 ЗАКОН РАСПРЕДЕЛЕНИЯ
Законом распределения случайной величины называется всякое соотношение, устанавливающее
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Слайд 7Рассмотрим дискретную случайную величину X с возможными значениями x1, х2, …,
Обозначим вероятности этих событий буквами р с соответствующими индексами:
Р(Х=х1)=р1; Р(Х=х2) = р2; ...; Р(Х = хn) = рn.
Так как несовместные события образуют полную группу, то сумма вероятностей всех возможных значений случайной величины равна единице
Слайд 8Ряд распределения случайной величины X имеет следующий вид
Чтобы придать ряду распределения
Слайд 10Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную
Слайд 13При построении многоугольника распределения надо помнить, что соединение полученных точек носит
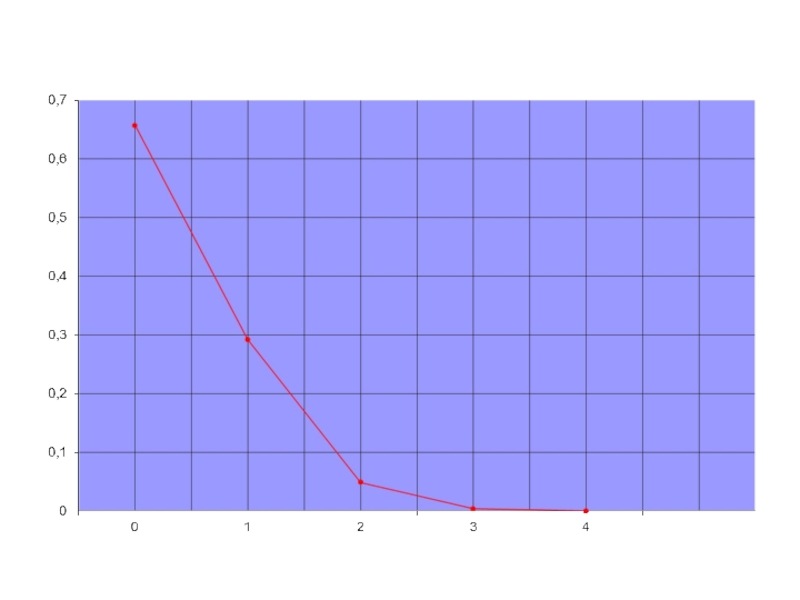
Слайд 14Биноминальное распределение
Если производится п независимых испытаний, в каждом
Примем число появлений события в каждом из испытаний за некоторую случайную величину Х.
Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.
Значения найти достаточно просто. Очевидно, что в результате п испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до п раз.
Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.
Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.
Слайд 18
Математическое ожидание
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений
, где
Х – прерывная случайная величина,
М[X] – среднее значение случайной величины,
– возможные значения величины Х,
p1, р2, р3,…,рn – вероятности значений.
Слайд 20Свойства математического ожидания:
Математическое ожидание постоянной величины равно самой постоянной.
Постоянный множитель можно
Слайд 213. Математическое ожидание произведения двух независимых случайных величин равно произведению их
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
Свойства математического ожидания:
Слайд 22
Пусть производится п независимых испытаний, вероятность появления события А в которых
Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Слайд 23Дисперсия
Дисперсией (рассеиванием) D(X) дискретной случайной величины называется математическое ожидание квадрата отклонения
Слайд 25Теорема
Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и
Слайд 26Свойства дисперсии:
Дисперсия постоянной величины равна нулю.
Постоянный множитель можно выносить за знак
Слайд 27Свойства дисперсии:
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих
Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Слайд 28Теорема
Дисперсия числа появления события А в п независимых испытаний, в каждом
Слайд 29Среднее квадратическое отклонение
Средним квадратическим отклонением случайной величины Х называется квадратный корень
Слайд 30Теорема
Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно
Слайд 32Домашнее задание:
1. Письменный Д.Т. Конспект лекций по теории вероятности, математической статистики
гл.2,§2.1 – 2.7
2. конспект лекции
СВР: Составить опорный конспект по теории