- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случайные величины (лекция 3) презентация
Содержание
- 1. Случайные величины (лекция 3)
- 2. Дискретная случайная величина Случайная величина – величина,
- 3. Способы задания распределения вероятностей дискретной случайной величины
- 4. Биномиальное распределение Аналитическое выражение закона распределения
- 5. Биномиальное распределение. Пример. Монета брошена 5 раз.
- 6. Геометрическое распределение Геометрическая прогрессия – степени
- 7. Геометрическое распределение. Пример.
- 8. Гипергеометрическое распределение Вероятность того, что среди
- 9. Гипергеометрическое распределение. Пример.
- 10. Числовые характеристики дискретной случайной величины
- 11. Доказательства свойств М.о. Распределение такой «случайной»
- 12. Математическое ожидание числа появления события в независимых
- 13. Резюме
Слайд 1Математические методы в биологии
Блок 2. Случайные величины
Лекция 3
Козлова Ольга Сергеевна
89276755130, olga-sphinx@yandex.ru
Слайд 2Дискретная случайная величина
Случайная величина – величина, которая в результате испытания принимает
Пример. Выпадение определённого числа очков на игральной кости (от 1 до 6). Число очков – случайная величина.
Дискретная случайная величина – случайная величина, которая может принимать конечные, изолированные значения из некоторого числового промежутка
Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого числового промежутка
Пример. Содержание какого-либо фермента в крови
Закон распределения вероятностей дискретной случайной величины – это сопоставление всех возможных значений случайной величины и их вероятностей.
Тривиальный пример. Случайная величина – сторона монетки. Она принимает два изолированных значения – либо «орёл», либо «решка» и подчинена следующему закону распределения:
Название случайной величины
Вектор вероятностей
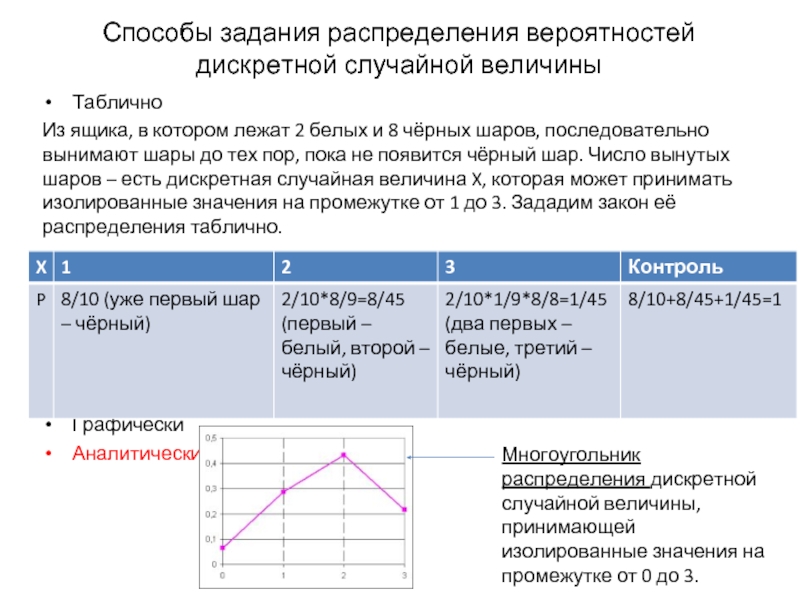
Слайд 3Способы задания распределения вероятностей дискретной случайной величины
Таблично
Из ящика, в котором лежат
Графически
Аналитически
Многоугольник распределения дискретной случайной величины, принимающей изолированные значения на промежутке от 0 до 3.
Слайд 4Биномиальное распределение
Аналитическое выражение закона распределения д.с.в.
Определение. Биномиальное распределение – это
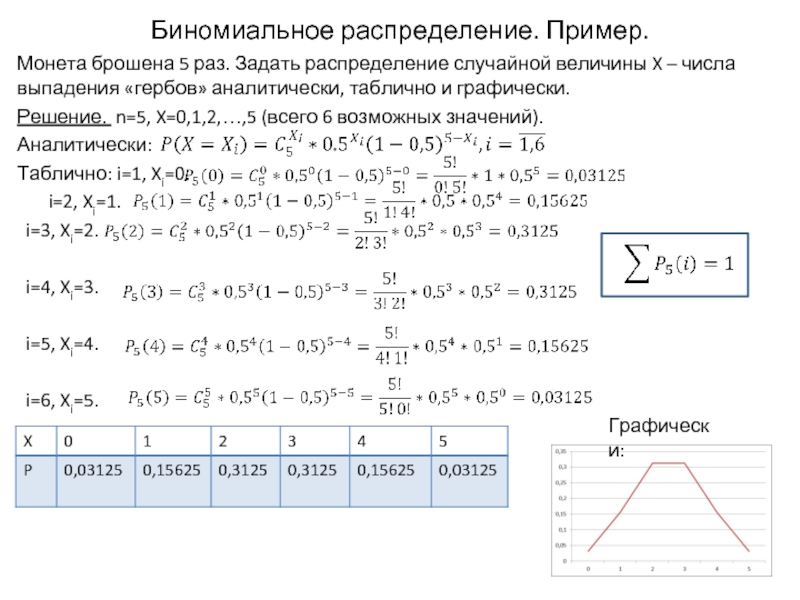
Слайд 5Биномиальное распределение. Пример.
Монета брошена 5 раз. Задать распределение случайной величины X
Решение. n=5, X=0,1,2,…,5 (всего 6 возможных значений).
Аналитически:
Таблично: i=1, Xi=0.
i=2, Xi=1.
i=3, Xi=2.
i=4, Xi=3.
i=5, Xi=4.
i=6, Xi=5.
Графически:
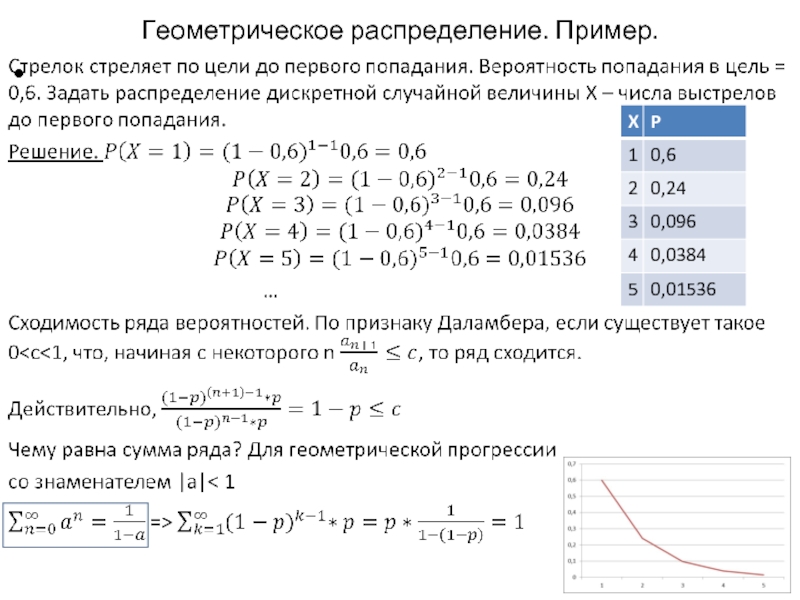
Слайд 6Геометрическое распределение
Геометрическая прогрессия – степени числа (1-p)
Определение. Геометрическое распределение – это
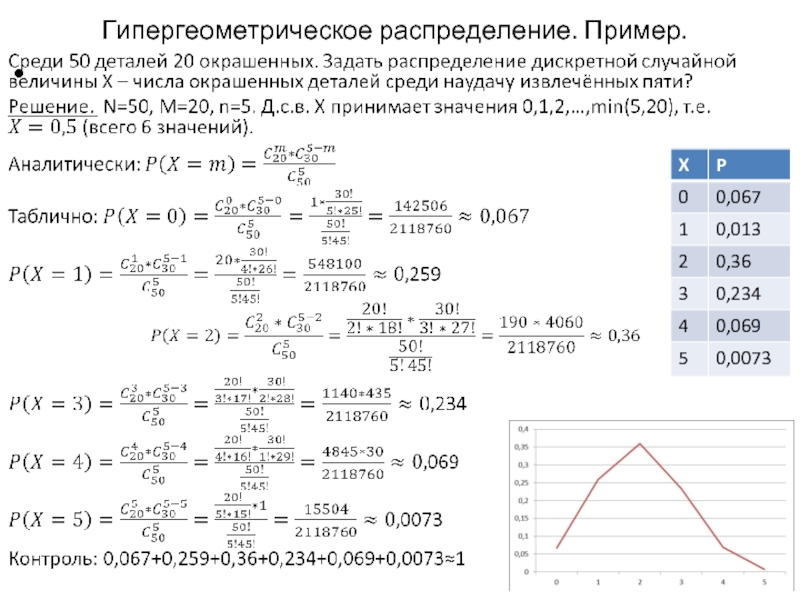
Слайд 8Гипергеометрическое распределение
Вероятность того, что среди n деталей будет ровно m без
Гипергеометрическое распределение определяется тремя параметрами –
N, M и n.
Слайд 10Числовые характеристики дискретной случайной величины
Независ.д.с.в. – те д.с.в., закон распределения которых
Слайд 11Доказательства свойств М.о.
Распределение такой «случайной» величины в табл. форме
*
=
p1
p2
q1
q2
+
=
Слайд 12Математическое ожидание числа появления события в независимых испытаниях
n независимых испытаний
Событие A
Дискретная случайная величина X – число появления события A в этих испытаниях
ВОПРОС: Чему равно среднее число (математическое ожидание случайной величины X) появлений события A в испытаниях?
ОТВЕТ: Математическое ожидание числа появлений события A в n испытаниях равно произведению n на p: M(X)=n*p
Доказательство. Пусть X1 – число появления события A в первом испытании, X2 – во втором и.т.д, Xn – в n-ом. Всего событие A появилось X1+X2+…+Xn раз. По свойству математического ожидания суммы, M(X)=M(X1)+M(X2)+…+M(Xn). Так как математическое ожидание числа появлений события в одном испытании равно его вероятности, M(X1)=M(X2)=…=M(Xn)=p. Отсюда M(X)=n*p.
Данная случайная величина X распределена по биномиальному закону, поэтому можно сказать, что МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПАРАМЕТРАМИ N И P РАВНО ПРОИЗВЕДЕНИЮ N*P.