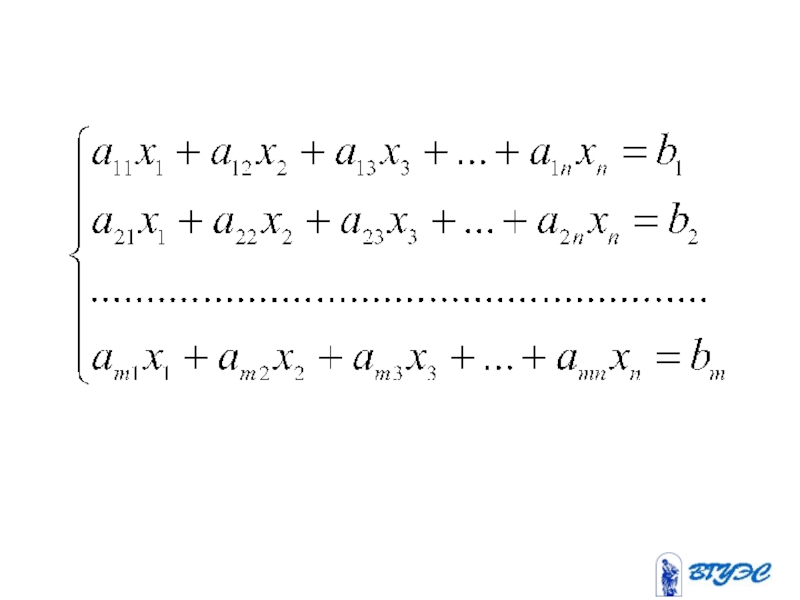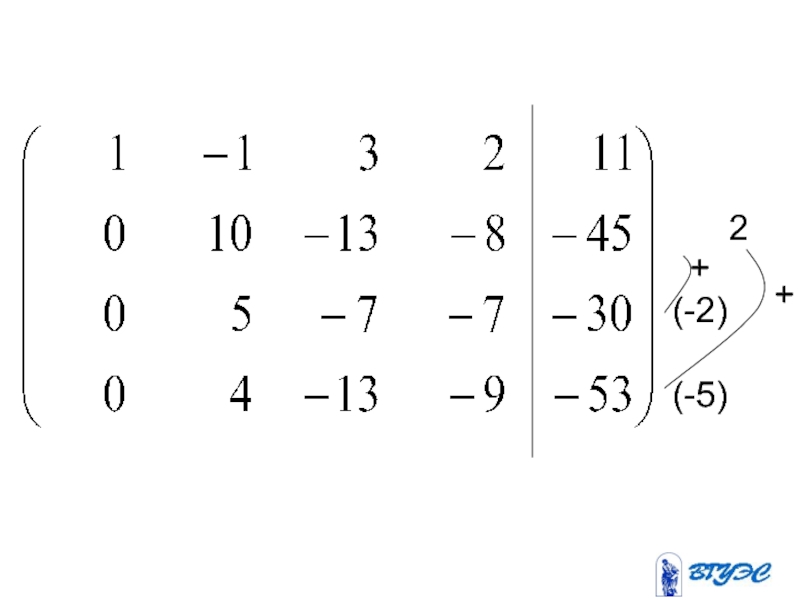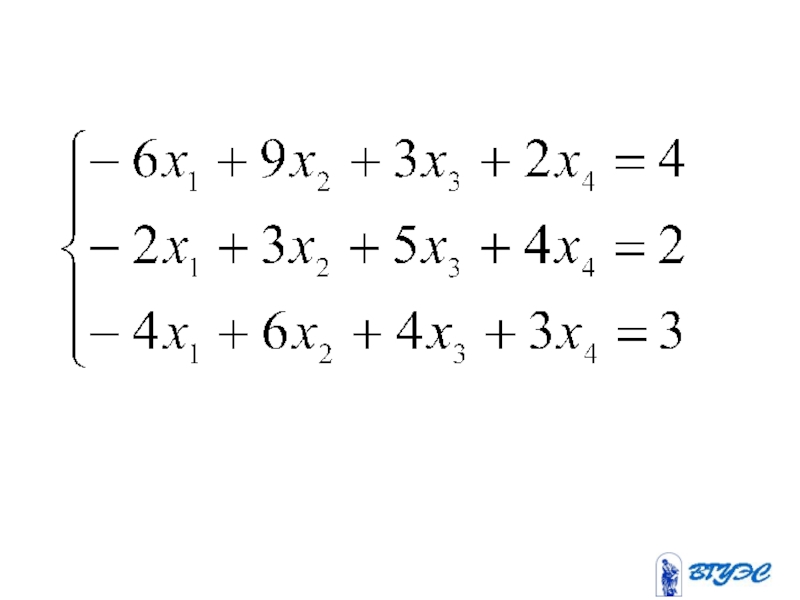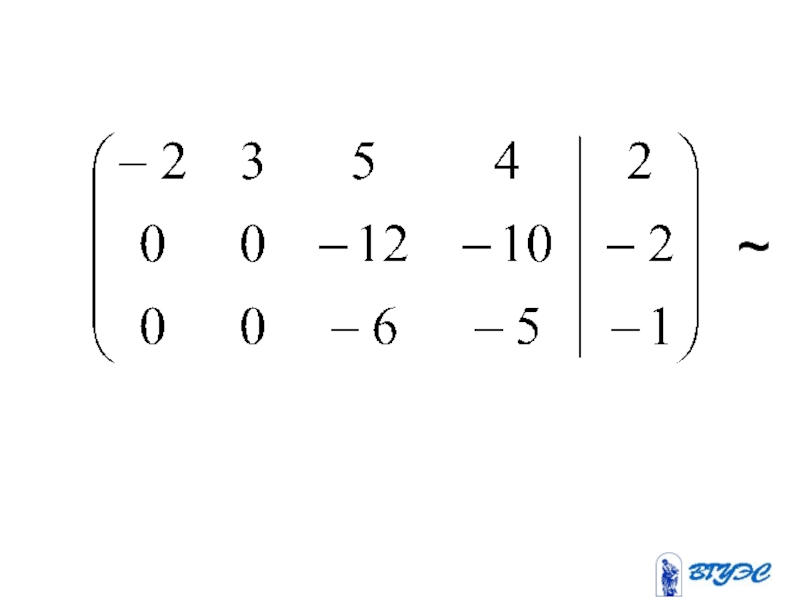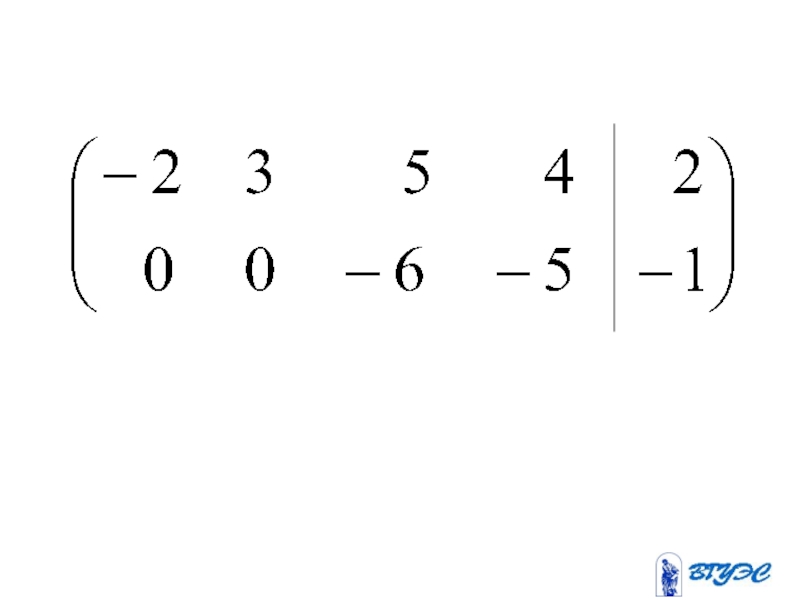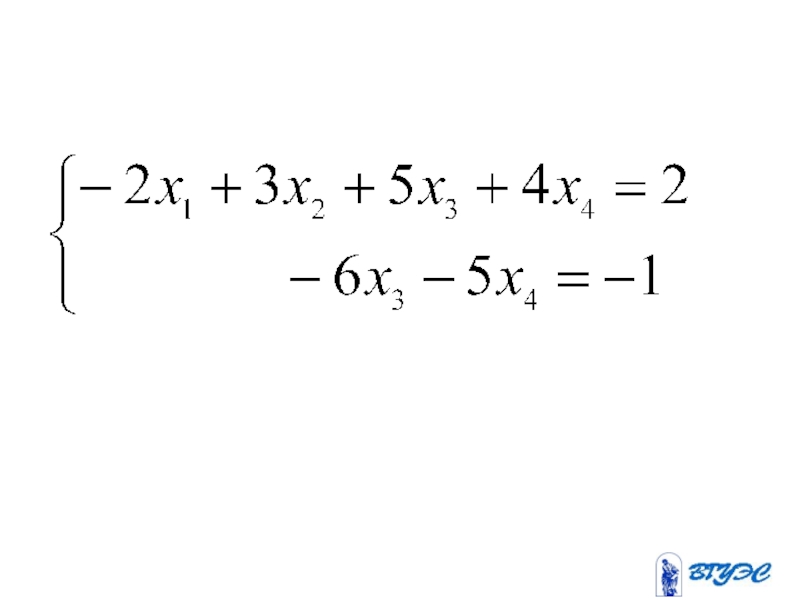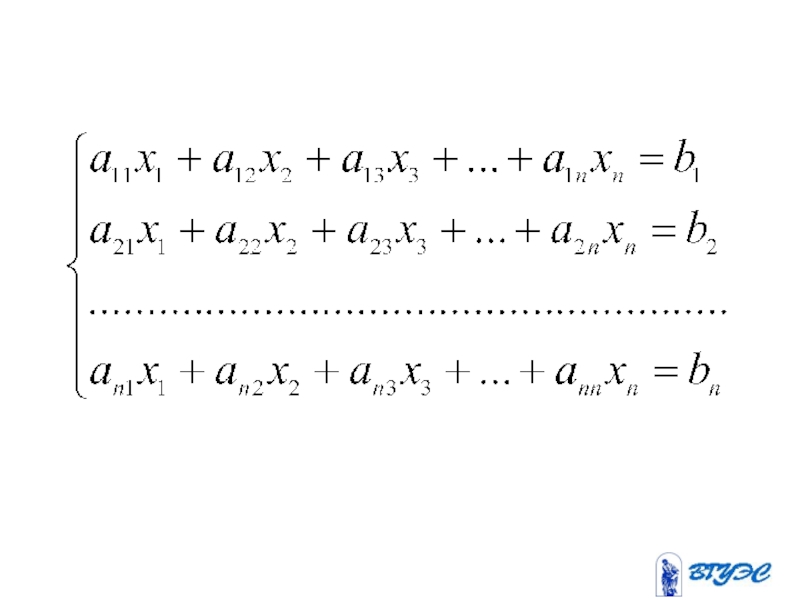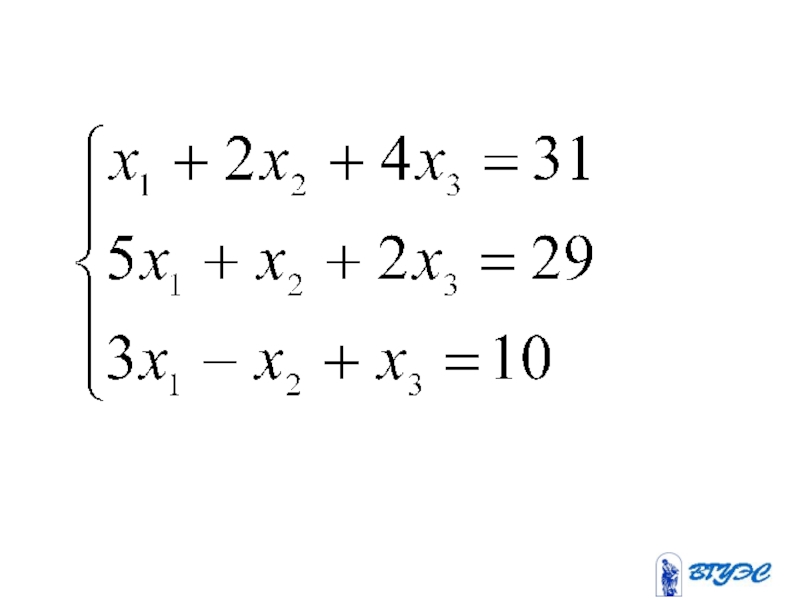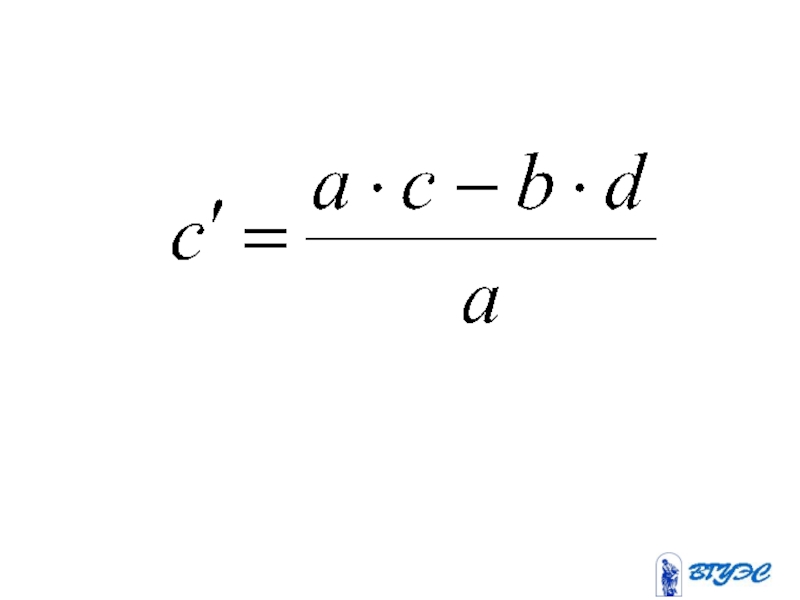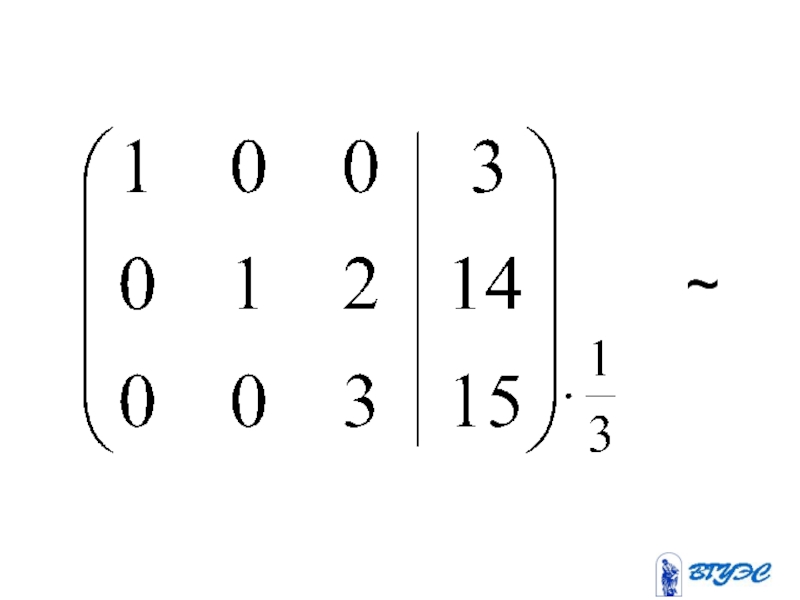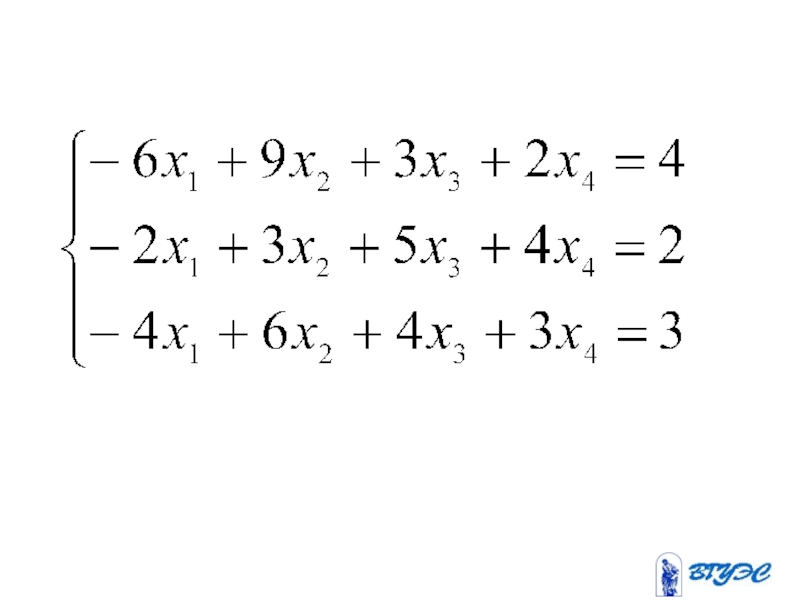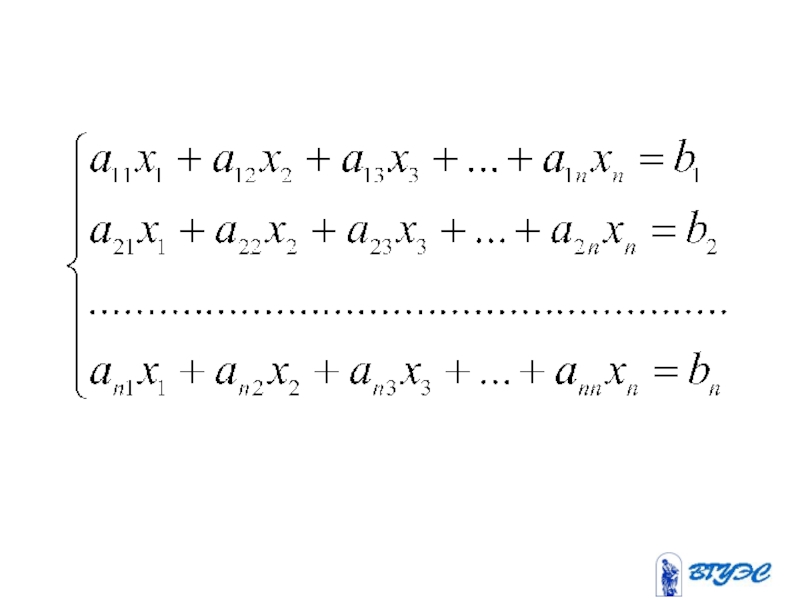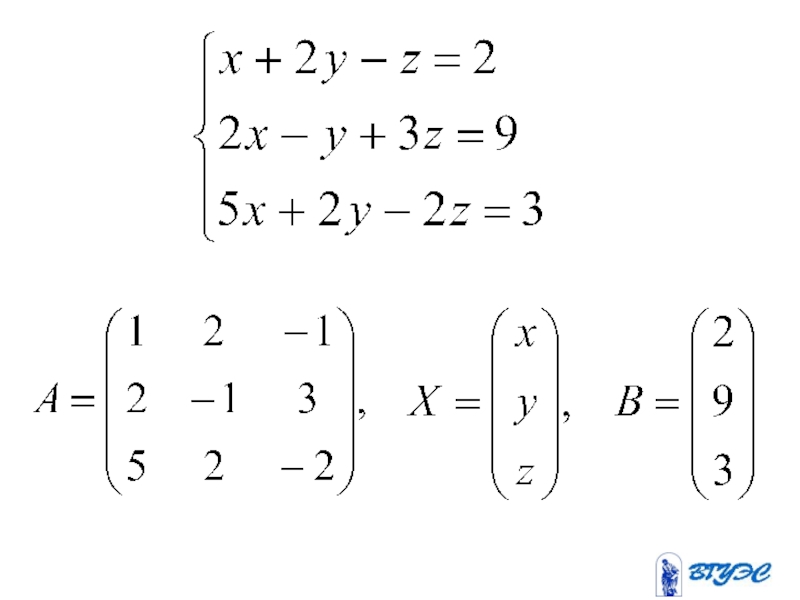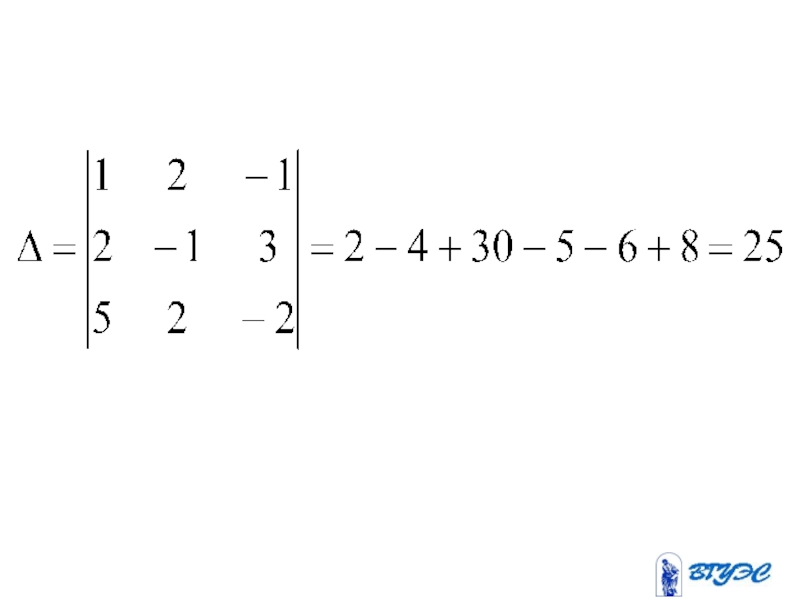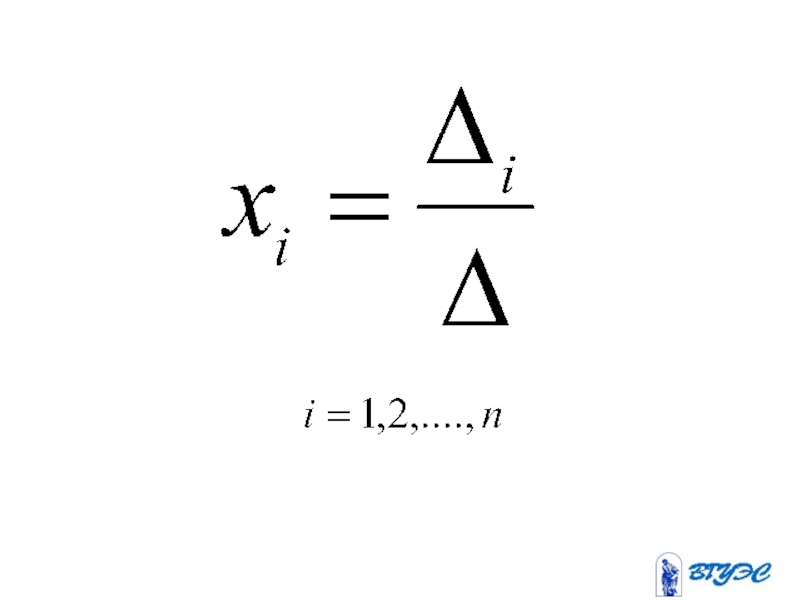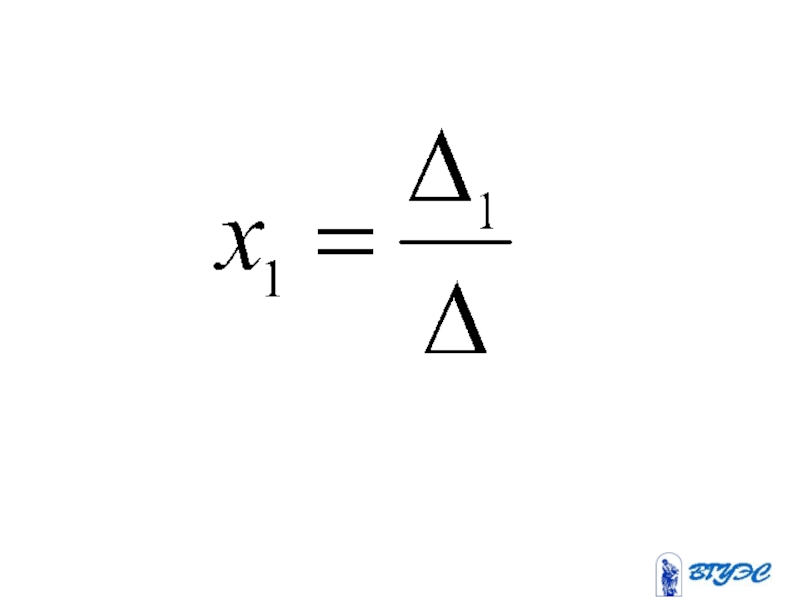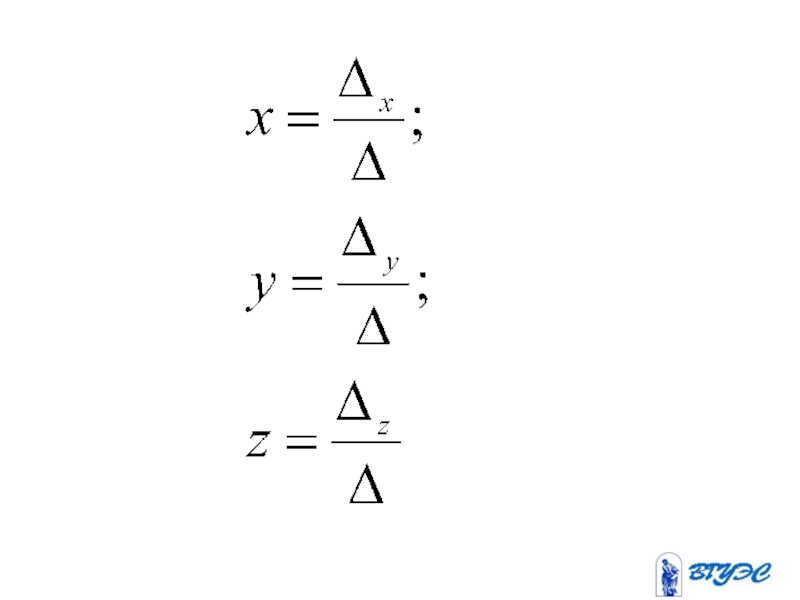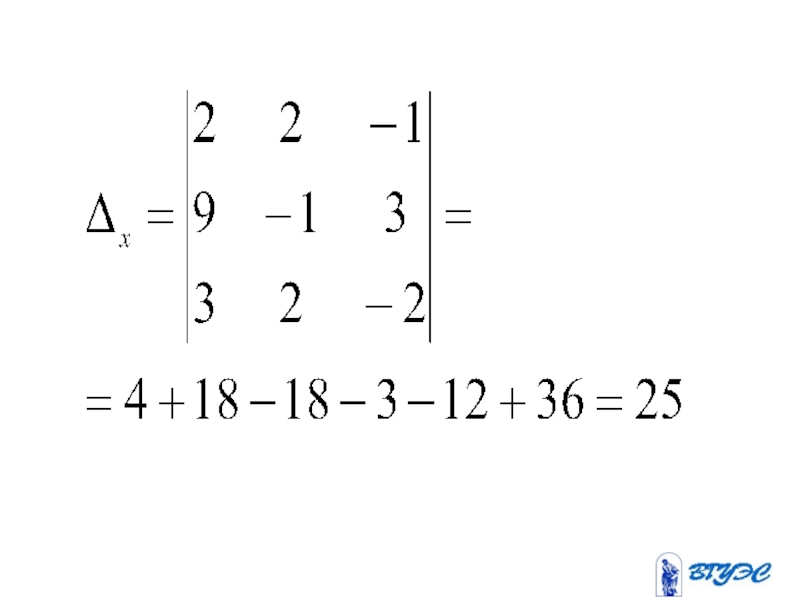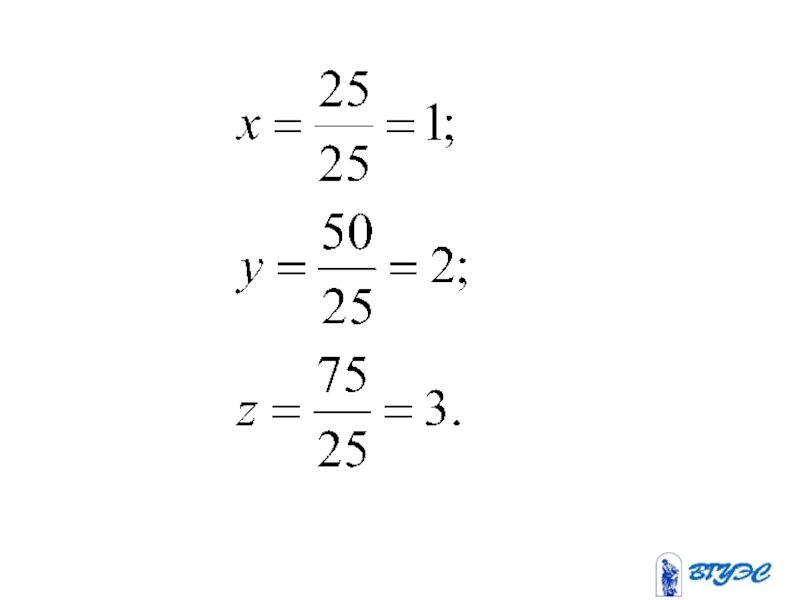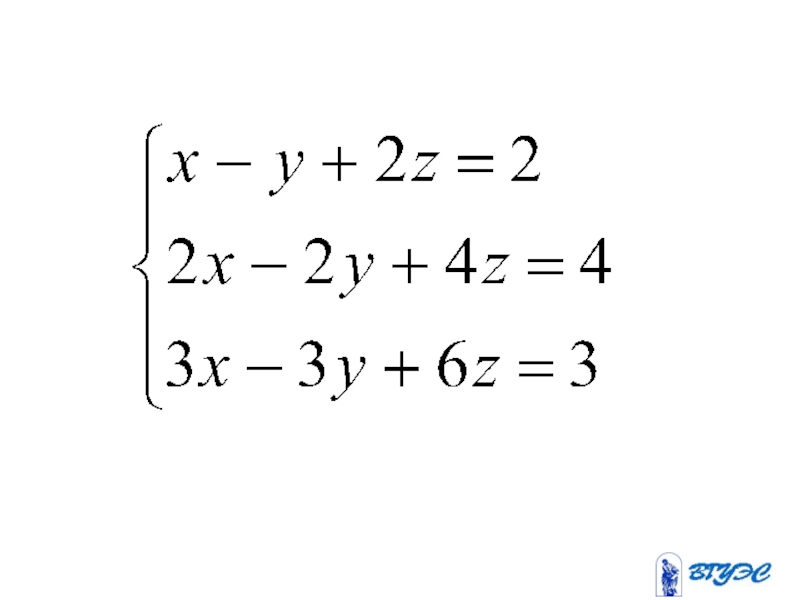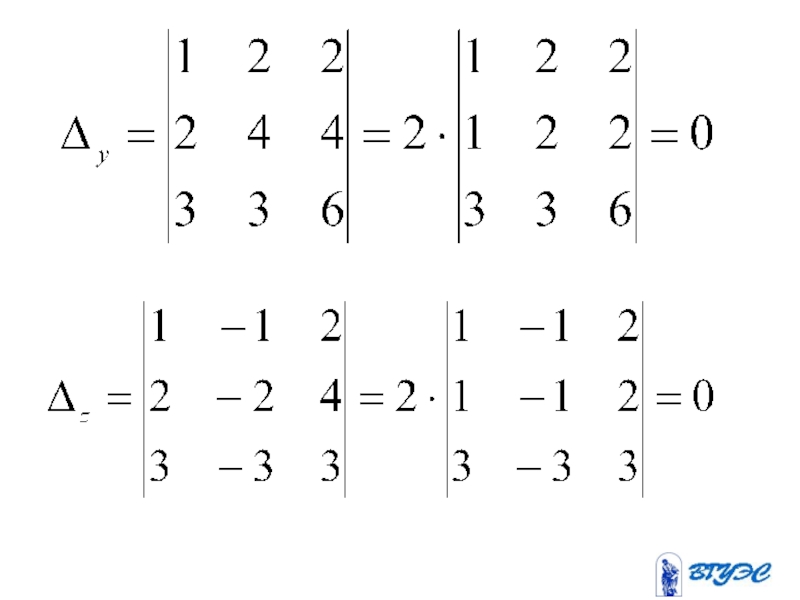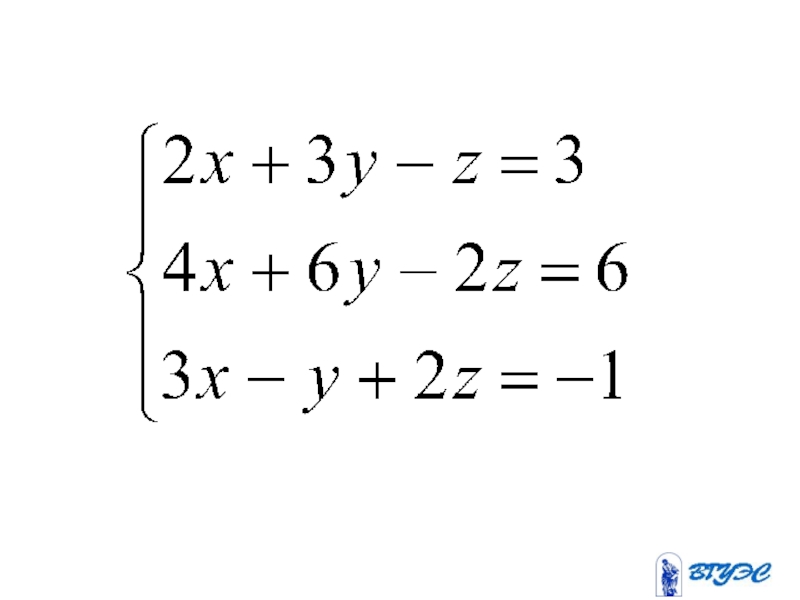- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы линейных алгебраических уравнений презентация
Содержание
- 1. Системы линейных алгебраических уравнений
- 3. Здесь
- 4. Система наз. неоднородной, если не все
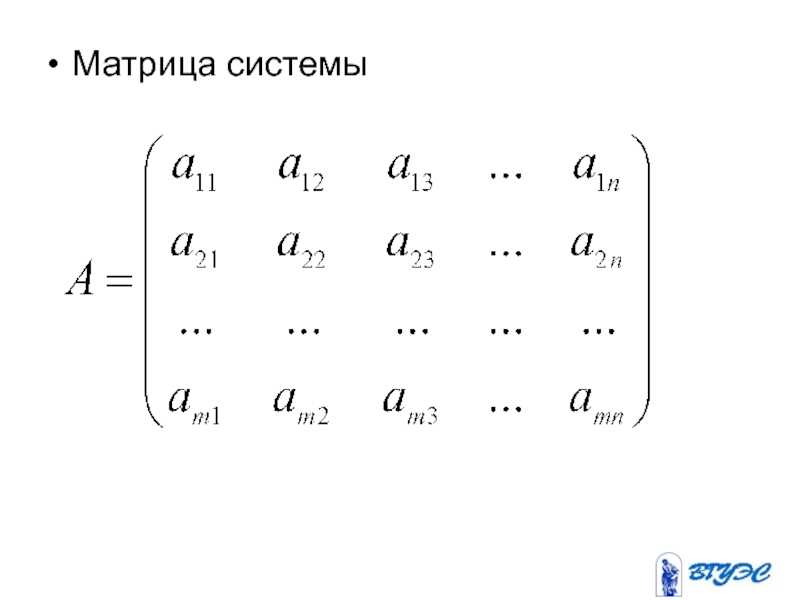
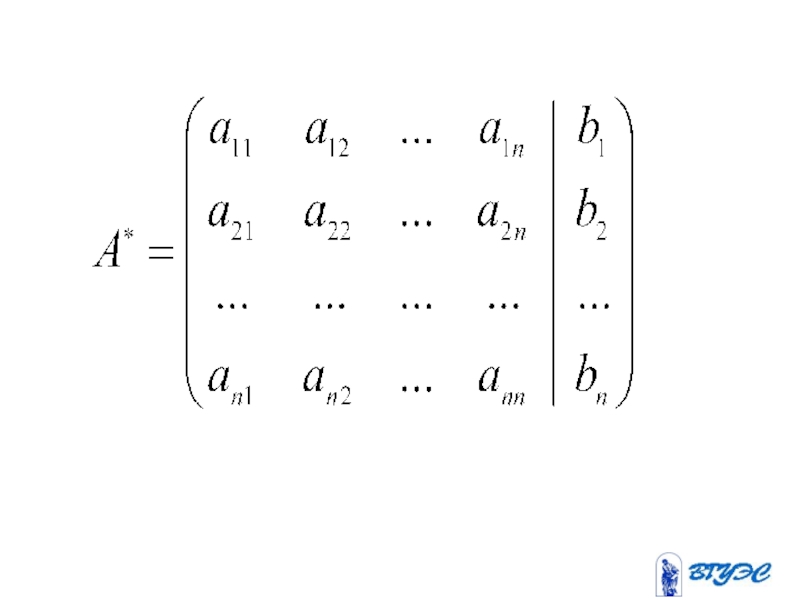
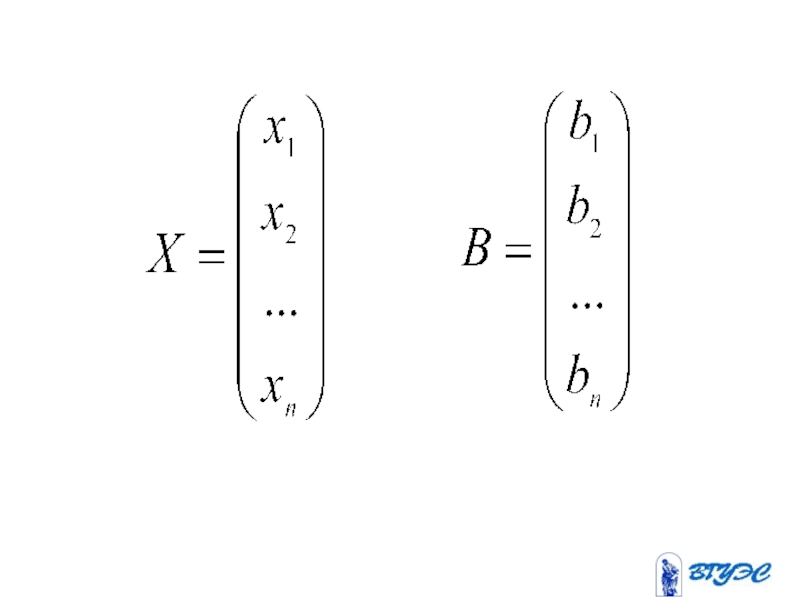
- 5. Матрица системы
- 6. Расширенная матрица
- 7. Решением системы будем называть
- 8. Решить систему — значит найти все
- 9. Если система не имеет
- 10. Две системы, множества
- 11. Метод Гаусса
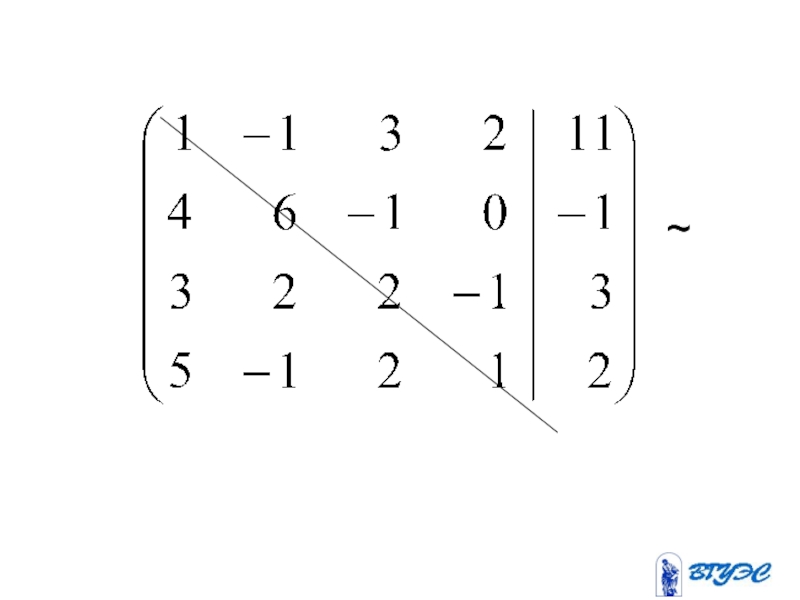
- 12. Рассмотрим квадратную систему:
- 16. (-2) (-5) 2 + +
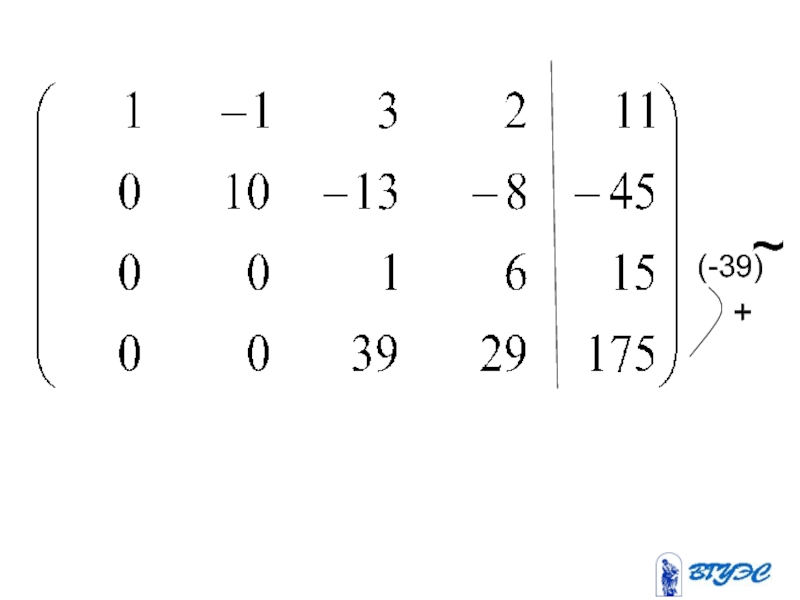
- 17. (-39) + ~
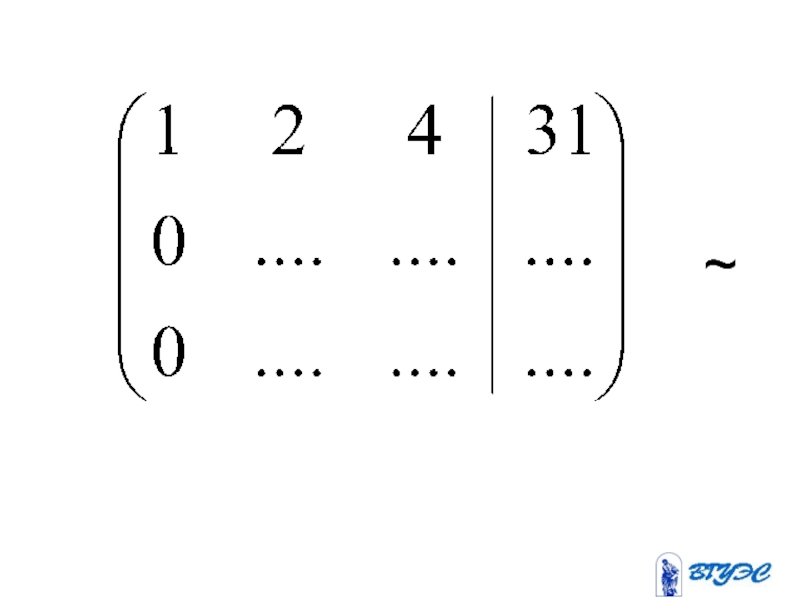
- 19. Полученная матрица соответствует системе:
- 22. ~
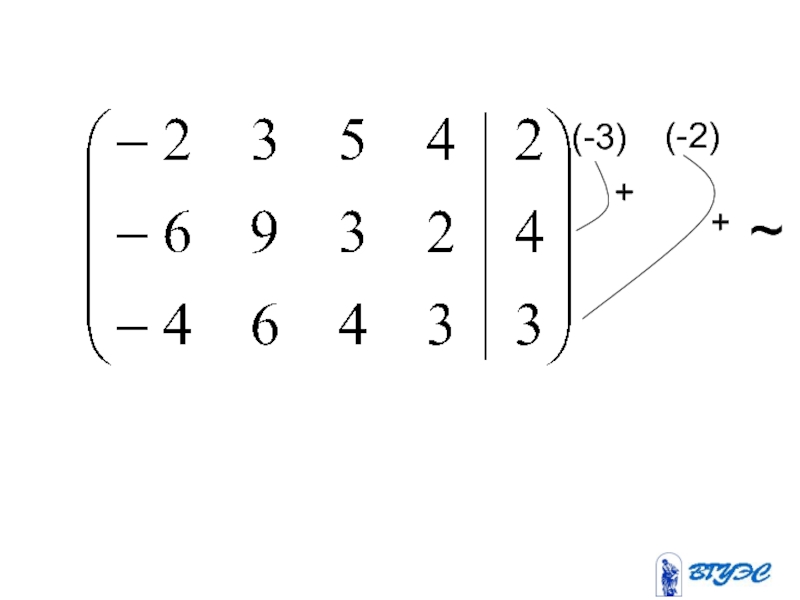
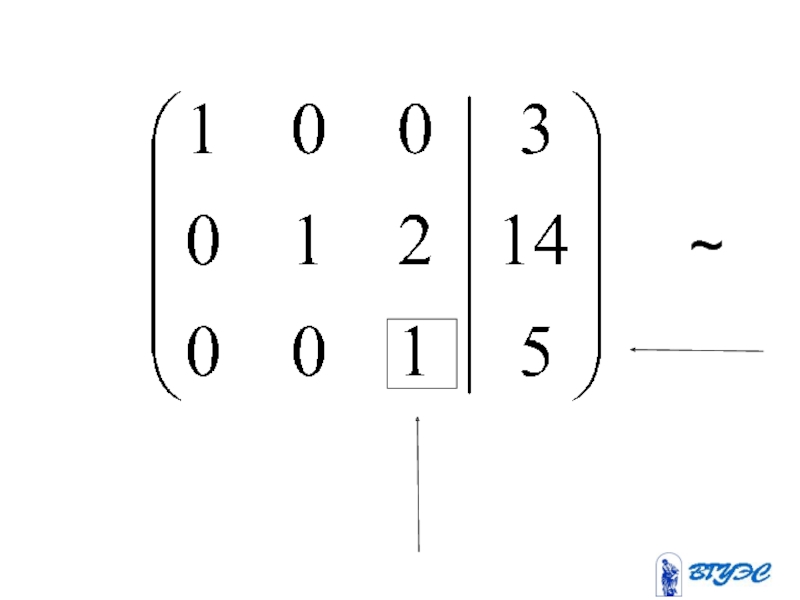
- 23. (-3) (-2) + + ~
- 24. ~
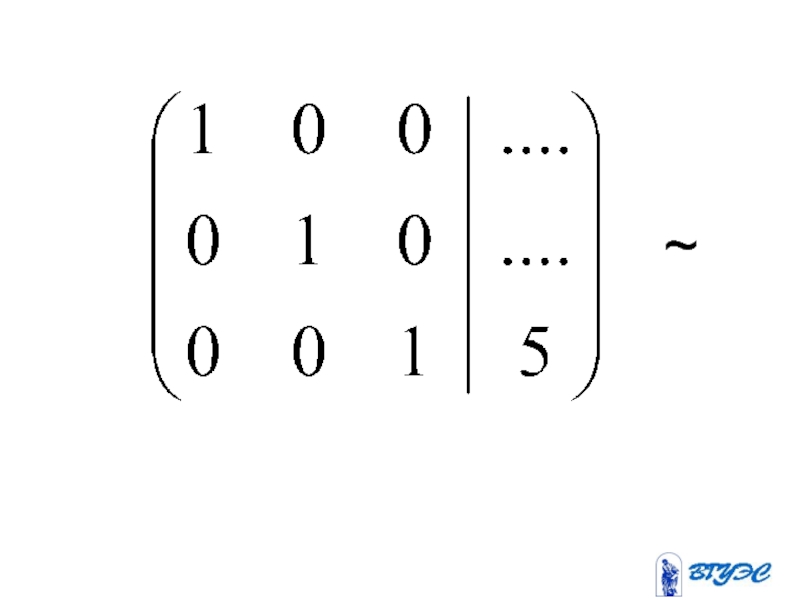
- 25. (-2) + ~
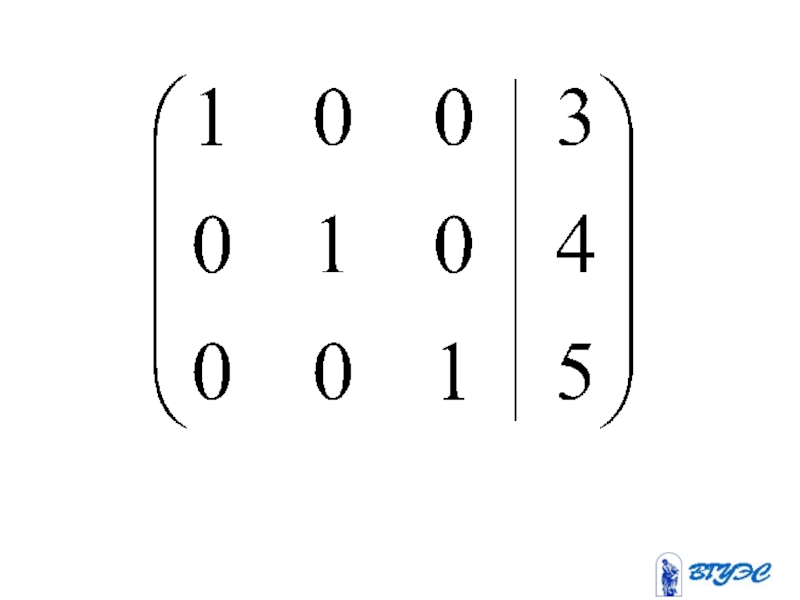
- 26. ~
- 28. Рассмотрим минор
- 34. Метод Жордана-Гаусса
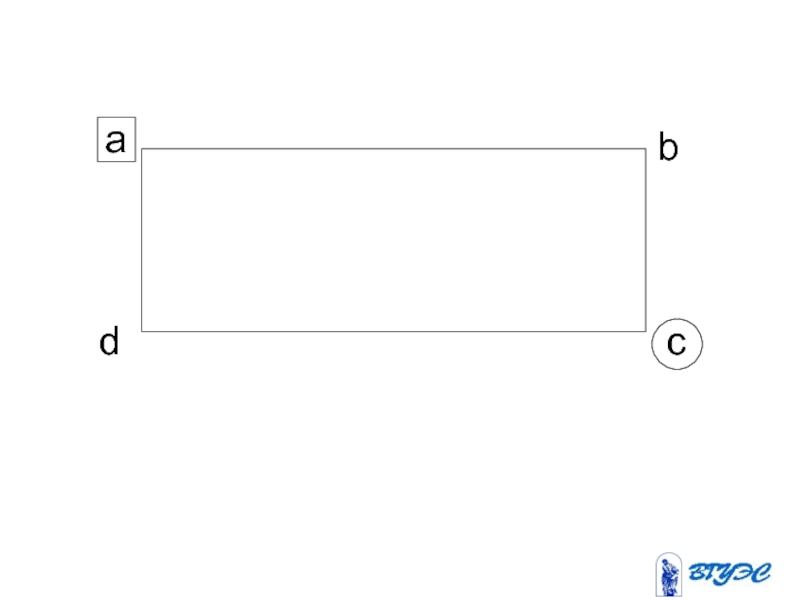
- 40. a c b d
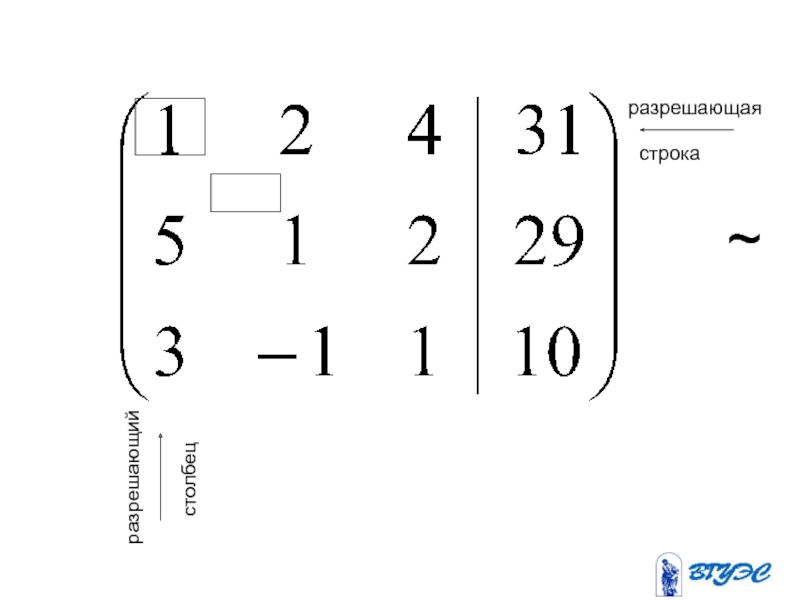
- 42. разрешающая разрешающий строка столбец ~
- 43. ~
- 44. ~
- 45. ~
- 46. ~
- 47. ~
- 48. ~
- 49. ~
- 50. ~
- 54. ~
- 55. ~
- 56. ~
- 57. ~
- 58. ~
- 59. ~
- 64. Матричный метод
- 65. С помощью этого метода можно решать квадратные системы линейных уравнений
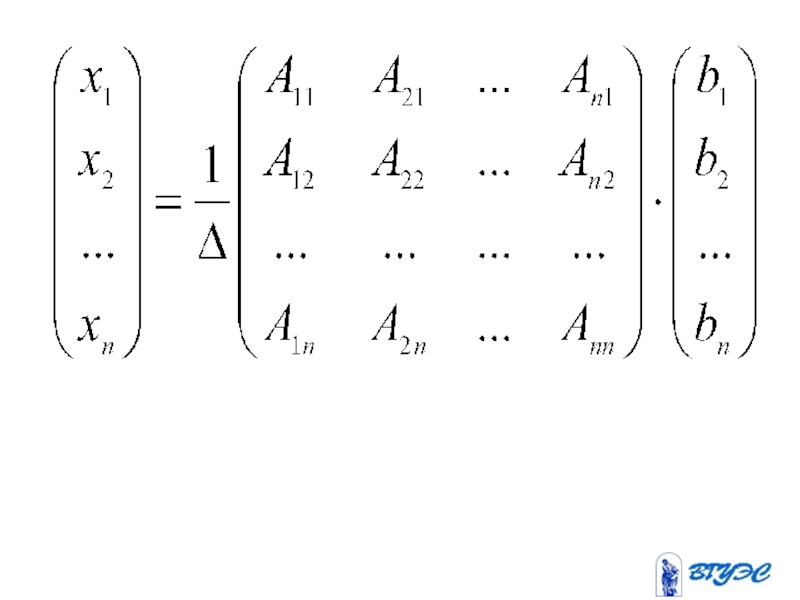
- 67. Систему можно записать в виде где (1)
- 69. Если матрица невырожденная,
- 81. Метод Крамера
- 82. Если определитель системы линейных
- 85. Здесь –
- 96. Если
- 100. Система не имеет решения, т.к. первое и третье уравнения противоречивы
- 104. Второе уравнение получается умножением первого на
- 108. Т е о р е м а
- 109. Замечание. Пусть система совместна и
- 110. (-2) (-5) ~
- 111. (-2) ~
- 114. Однородные системы
- 115. Теорема о совместности
Здесь - неизвестные; - коэффициенты при неизвестных, где
Слайд 3Здесь
- неизвестные;
- коэффициенты при неизвестных,
где - номер уравнения,
- номер неизвестного;
- свободные члены (правые части).
- коэффициенты при неизвестных,
где - номер уравнения,
- номер неизвестного;
- свободные члены (правые части).
Слайд 4Система наз. неоднородной, если не все равны
нулю.
Система наз. однородной, если все
равны нулю.
Система наз. однородной, если все
равны нулю.
Слайд 7 Решением системы будем называть
упорядоченный набор чисел
обращающий каждое
уравнение
системы в верное равенство.
системы в верное равенство.
Слайд 8Решить систему — значит найти
все ее решения или доказать, что
ни
одного решения нет.
Система, имеющая хотя бы одно
решение, называется совместной.
Если система имеет только одно
решение, то она называется
определенной.
одного решения нет.
Система, имеющая хотя бы одно
решение, называется совместной.
Если система имеет только одно
решение, то она называется
определенной.
Слайд 9Если система не имеет решений, то
она
называется несовместной.
Система, имеющая более чем одно
решение, называется неопределенной
(совместной и неопределенной).
Если число уравнений системы
совпадает с числом неизвестных , то
система называется квадратной.
Система, имеющая более чем одно
решение, называется неопределенной
(совместной и неопределенной).
Если число уравнений системы
совпадает с числом неизвестных , то
система называется квадратной.
Слайд 10Две системы, множества решений
которых совпадают,
называются
эквивалентными или равносильными.
Преобразование, применение которого
превращает систему в новую
систему, эквивалентную исходной,
называется эквивалентным или
равносильным преобразованием.
эквивалентными или равносильными.
Преобразование, применение которого
превращает систему в новую
систему, эквивалентную исходной,
называется эквивалентным или
равносильным преобразованием.
Слайд 82Если определитель системы линейных уравнений с
неизвестными отличен от нуля, то эта система является определенной и её единственное решение находится по формулам
Слайд 85Здесь – определитель,
получающийся из определителя
заменой i-го столбца столбцом
свободных членов.
Слайд 96Если и по крайне мере
один из определителей , то система не имеет решения.
Если и , система либо не имеет решения, либо имеет бесконечно много решений.
Если и , система либо не имеет решения, либо имеет бесконечно много решений.
Слайд 104Второе уравнение получается
умножением первого на два. Данная система
равносильна системе
Система
имеет бесчисленное множество
решений.
решений.
Слайд 108Т е о р е м а К
р о н е к е р а - К а п е л л и
Для того чтобы система
неоднородных линейных уравнений
с неизвестными была совместной,
необходимо и достаточно, чтобы
Слайд 109Замечание. Пусть система совместна и
если число уравнений равно числу неизвестных, причем , то система имеет единственное решение;
если число уравнений меньше числа неизвестных, то система имеет множество решение.
если число уравнений меньше числа неизвестных, то система имеет множество решение.
Слайд 115 Теорема о совместности однородной системы
Для того чтобы однородная система
линейных уравнений имела решение,
необходимо и достаточно, чтобы ранг
матрицы этой системы был меньше числа
неизвестных n.
