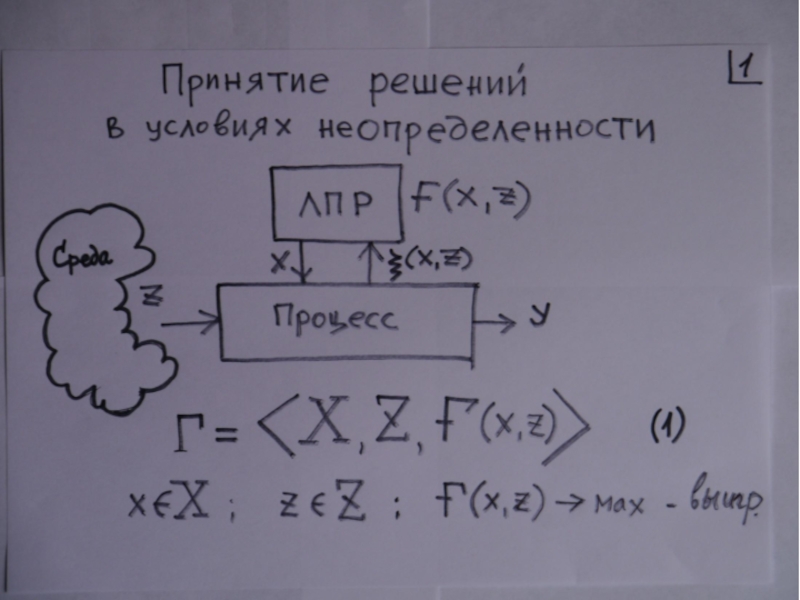
Системы одновременных уравнений
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы эконометрических уравнений презентация
Содержание
- 1. Системы эконометрических уравнений
- 2. Система независимых уравнений Каждая зависимая
- 3. Система рекурсивных уравнений В каждое последующее
- 4. Система одновременных (взаимозависимых) уравнений Одни
- 5. Структурная форма модели
- 6. Эндогенные переменные – зависимые переменные уравнений
- 7. Эконометрические модели,
- 8. Приведённая форма модели
- 9. КМНК – косвенный метод наименьших квадратов
- 10. Идентификация простейшей модели
- 11. Проблема идентификации Идентифицируемость
- 12. Структурные модели с точки зрения идентифицируемости
- 13. Необходимое условие идентифицируемости уравнения Обозначим: Н
- 14. Пример: Уравнение
- 15. Достаточное условие идентифицируемости уравнения Матрица
- 16. Методы оценивания структурных коэффициентов Косвенный МНК (КМНК)
- 17. ДМНК – двухшаговый метод наименьших квадратов Шаг
Слайд 1Тема 3: Системы эконометрических уравнений
Системы независимых уравнений
Системы рекурсивных уравнений
Слайд 2Система независимых уравнений
Каждая зависимая переменная есть функция одного и
того же набора факторов х:
Пример: модель экономической эффективности с/х производства, где
- показатели эффективности
Пример: модель экономической эффективности с/х производства, где
- показатели эффективности
Слайд 3Система рекурсивных уравнений
В каждое последующее
уравнение входят в
качестве факторов
зависимые
переменные
предшествующих уравнений
Пример: модель производительности труда ( ) и фондоотдачи ( ):
предшествующих уравнений
Пример: модель производительности труда ( ) и фондоотдачи ( ):
Слайд 4Система одновременных (взаимозависимых) уравнений
Одни и те же переменные
одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других урав-нениях. Обычный МНК неприменим ( он даёт смещённые и несостоятельные оценки).
Пример: модель динамики цен ( ) и заработной платы ( ):
Пример: модель динамики цен ( ) и заработной платы ( ):
Слайд 5Структурная форма модели
Это исходная форма системы одновременных
уравнений, полученная на основе описания существующих реальных связей между переменными (структурная модель).
Простейшая структурная модель (в центрированных переменных):
– структурные коэффициенты
Простейшая структурная модель (в центрированных переменных):
– структурные коэффициенты
Слайд 6
Эндогенные переменные – зависимые переменные уравнений
Экзогенные переменные – предопреде-лённые переменные, влияющие
на эндогенные, но не зависящие от них
В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные)
В качестве экзогенных переменных целесообразно выбирать регулируемые переменные
В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные)
В качестве экзогенных переменных целесообразно выбирать регулируемые переменные
Слайд 7
Эконометрические модели, кроме уравнений взаимосвязи, могут включать
в систему тождества.
Например, модель зависимости потребления (С) от дохода ( ) учитывает тождество дохода:
I– инвестиции.
При этом оценки параметров должны учитывать тождество дохода
Слайд 8Приведённая форма модели
Для корректности применения МНК структурная
форма модели преобразует-ся в систему линейных уравнений зави-симости эндогенных переменных от экзогенных.
Для простейшей модели:
(система независимых уравнений)
– приведённые коэффициенты
Для простейшей модели:
(система независимых уравнений)
– приведённые коэффициенты
Слайд 9КМНК – косвенный метод наименьших квадратов
Приведённые коэффициенты можно
найти путём обычных алгебраических преобразований.
МНК-оценки приведённых коэффициентов используются для определения структурных коэффициентов путём обратных алгебраических преобразований.
МНК-оценки приведённых коэффициентов используются для определения структурных коэффициентов путём обратных алгебраических преобразований.
Слайд 11Проблема идентификации
Идентифицируемость – это единственность соответствия между
приведённой и структурной формами модели.
При обратном переходе от приведённой мо-
дели к структурной может возникнуть проблема
неоднозначности между совокупностью приве-
дённых и структурных коэффициентов.
КМНК можно использовать лишь при нали-чии их взаимнооднозначного соответствия
При обратном переходе от приведённой мо-
дели к структурной может возникнуть проблема
неоднозначности между совокупностью приве-
дённых и структурных коэффициентов.
КМНК можно использовать лишь при нали-чии их взаимнооднозначного соответствия
Слайд 12Структурные модели с точки зрения идентифицируемости
можно разделить на 3 вида:
идентифицируемые
неидентифицируемые
сверхидентифицируемые
Модель идентифицируема, если идентифициру-
емо каждое уравнение системы.
Если хотя бы одно уравнение неидентифицируе-
мо, то вся модель неидентифицируема. Сверхидентифицируемая модель содержит хотя
бы одно сверхидентифицируемое уравнение.
емо каждое уравнение системы.
Если хотя бы одно уравнение неидентифицируе-
мо, то вся модель неидентифицируема. Сверхидентифицируемая модель содержит хотя
бы одно сверхидентифицируемое уравнение.
Слайд 13Необходимое условие идентифицируемости уравнения
Обозначим:
Н – число эндогенных переменных системы,
присутствующих в данном уравнении;
D – число экзогенных переменных системы,
отсутствующих в данном уравнении
Если D + 1 = H – уравнение идентифицируемо
Если D + 1 < H – уравнение неидентифицируемо
Если D + 1 > H – уравнение сверхидентифицируемо
D – число экзогенных переменных системы,
отсутствующих в данном уравнении
Если D + 1 = H – уравнение идентифицируемо
Если D + 1 < H – уравнение неидентифицируемо
Если D + 1 > H – уравнение сверхидентифицируемо
Слайд 15Достаточное условие идентифицируемости уравнения
Матрица коэффициентов остальных уравнений системы, отсутствующих
в данном уравнении, невырожденна
( )
В примере для уравнения I получена матрица:
( )
В примере для уравнения I получена матрица:
Слайд 16Методы оценивания структурных коэффициентов
Косвенный МНК (КМНК) – для иденти-фицируемых уравнений
Двухшаговый МНК
(ДМНК) – для сверх-идентифицируемых уравнений
Трёхшаговый МНК – для всех видов урав-нений
Метод максимального правдоподобия (ММП) – общий метод
Трёхшаговый МНК – для всех видов урав-нений
Метод максимального правдоподобия (ММП) – общий метод
Слайд 17ДМНК – двухшаговый метод наименьших квадратов
Шаг 1: для приведённой формы модели
находят МНК-оценки коэффициентов. По оценённому уравнению определяют теоретические значения
эндогенных переменных, содержащихся в правой части сверхидентифицируемого уравнения;
Шаг 2: заменив в правой части сверхидентифи-цируемого уравнения фактические значения эндогенных переменных на теоретические, применяют обычный МНК для определения структурных коэффициентов данного уравнения.
эндогенных переменных, содержащихся в правой части сверхидентифицируемого уравнения;
Шаг 2: заменив в правой части сверхидентифи-цируемого уравнения фактические значения эндогенных переменных на теоретические, применяют обычный МНК для определения структурных коэффициентов данного уравнения.