- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение сечений тетраэдра и параллелепипеда (урок геометрии в 10 классе) презентация
Содержание
- 1. Построение сечений тетраэдра и параллелепипеда (урок геометрии в 10 классе)
- 2. 1 блок составного урока 3х30 Коррекция знаний по теме «Построение сечений тетраэдра и параллелепипеда»
- 3. 2. Изобразите эту поверхность в тетрадях. Вопросы
- 4. 8. Какие многоугольники могут получиться в сечении
- 5. 9. Какая плоскость называется секущей плоскостью параллелепипеда?
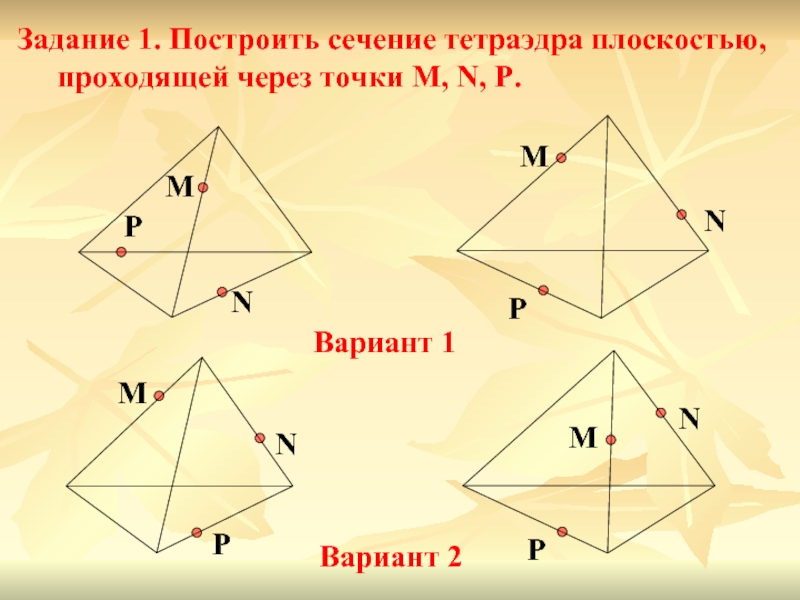
- 6. Решение задач Задание 1. Построить сечение тетраэдра
- 7. M N P M N P
- 8. M N
- 9. 2 блок составного урока 3х30 Срезовая работа
- 10. M N P Вариант
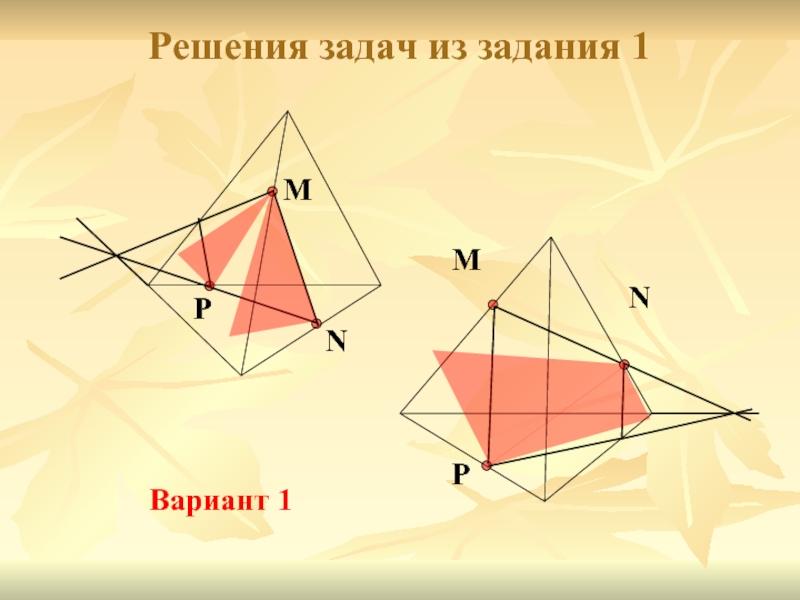
- 11. Решения задач из задания 1 M
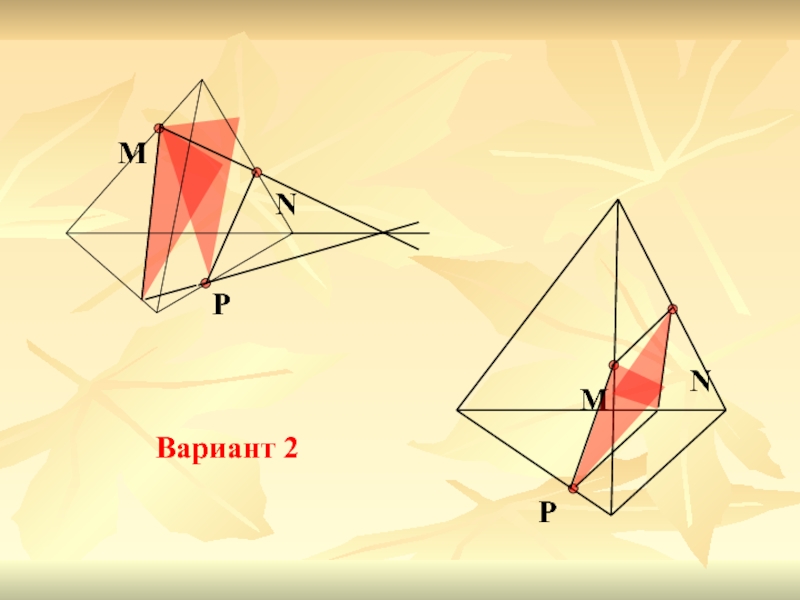
- 12. M N P M N P Вариант 2
- 13. Вариант 1 Вариант 2 M
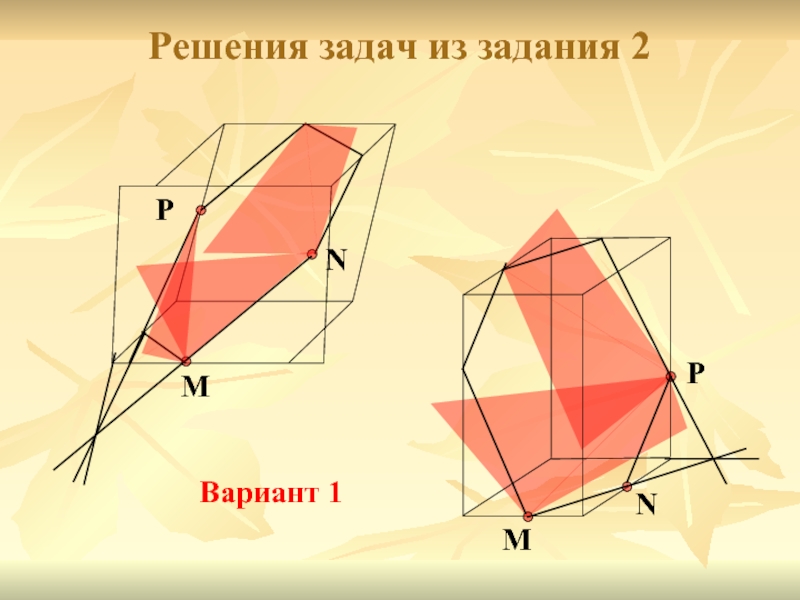
- 14. Решения задач из задания 2 M N
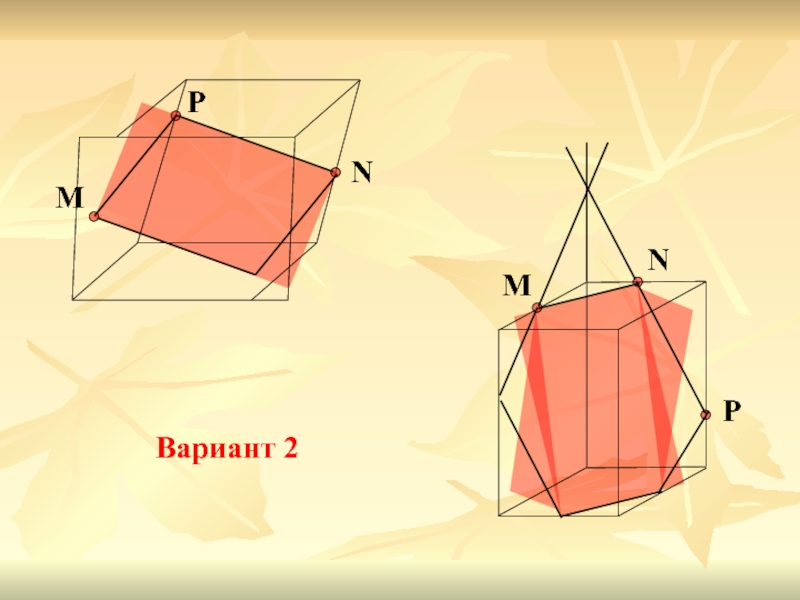
- 15. M N P M N P Вариант 2
- 16. 3 блок составного урока 3х30 Решение сложных
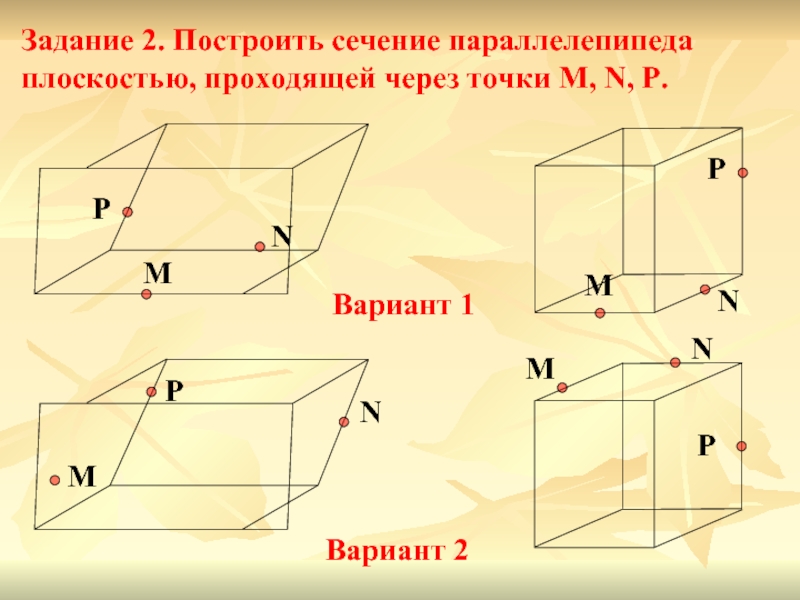
- 17. Задание 1. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью
- 18. A B C D A1 B1
- 19. Задание 2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью,
- 20. A B C D A1 B1
- 21. Задание 3. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью,
- 22. A B C D A1 B1 C1
- 23. Конец урока
1 блок составного урока 3х30 Коррекция знаний по теме «Построение сечений тетраэдра и параллелепипеда»
Слайд 21 блок составного урока 3х30
Коррекция знаний по теме «Построение сечений тетраэдра
и параллелепипеда»
Слайд 32. Изобразите эту поверхность в тетрадях.
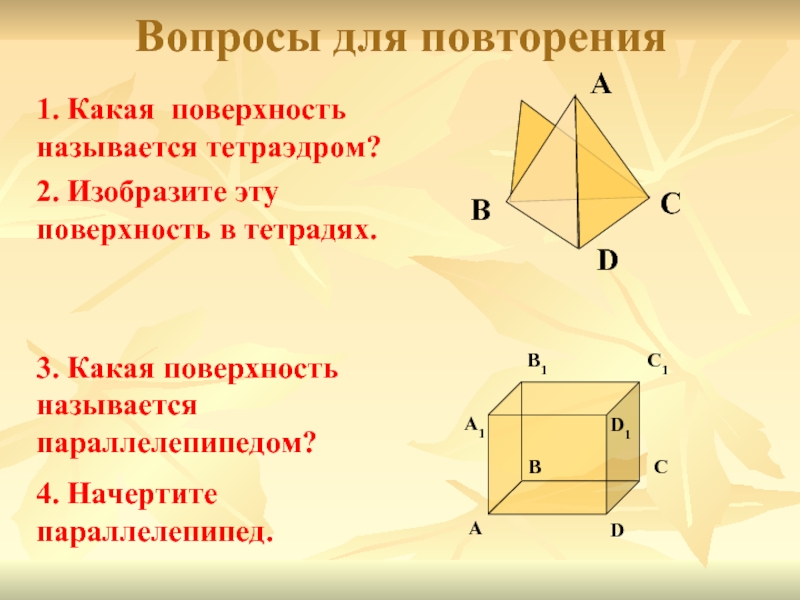
Вопросы для повторения
1. Какая поверхность называется
тетраэдром?
3. Какая поверхность называется параллелепипедом?
4. Начертите параллелепипед.
Слайд 48. Какие многоугольники могут получиться в сечении тетраэдра?
5. Какая плоскость называется
секущей плоскостью тетраэдра?
6. Что называется сечением тетраэдра?
7. Каким образом строится сечение тетраэдра?
M
N
P
Слайд 59. Какая плоскость называется секущей плоскостью параллелепипеда?
10. Что называется сечением параллелепипеда?
12.
Каким образом строится сечение параллелепипеда?
11. Какие многоугольники могут получиться в сечении параллелепипеда?
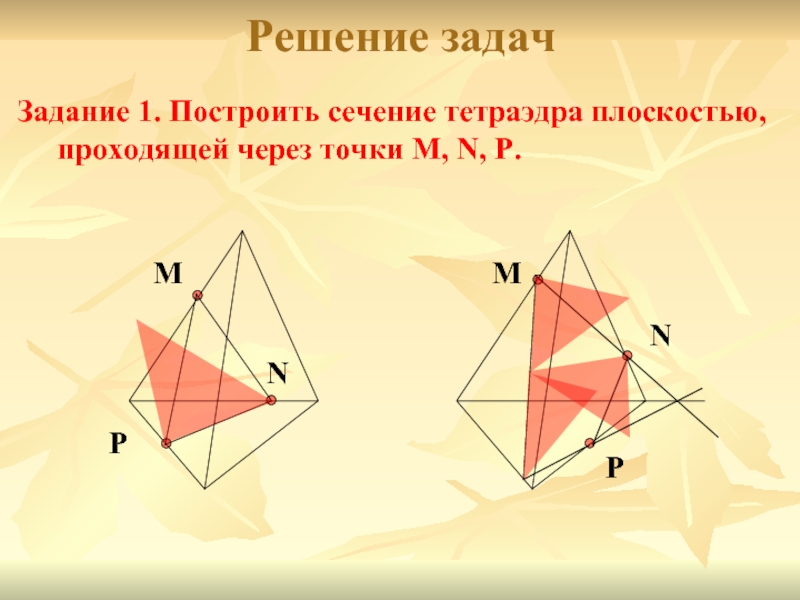
Слайд 6Решение задач
Задание 1. Построить сечение тетраэдра плоскостью, проходящей через точки M,
N, P.
M
N
P
M
N
P
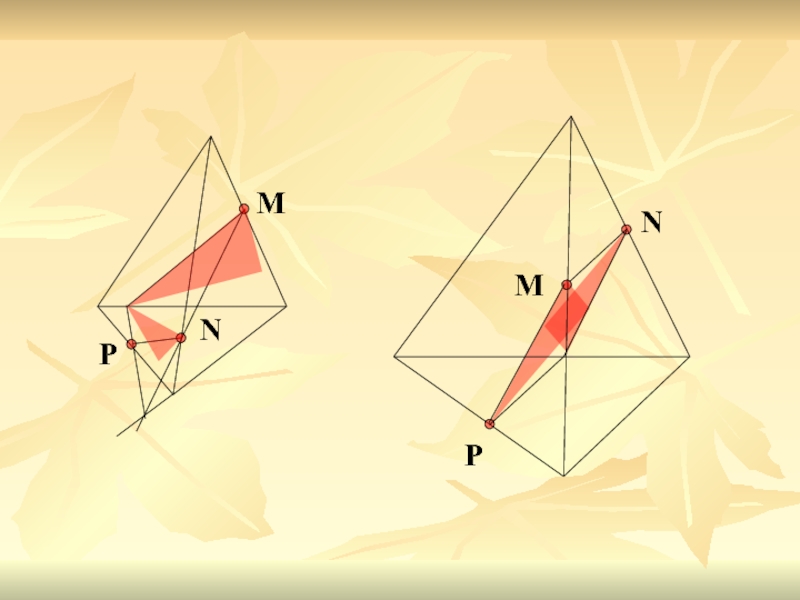
Слайд 8
M
N
P
M
N
P
M
N
P
N
M
P
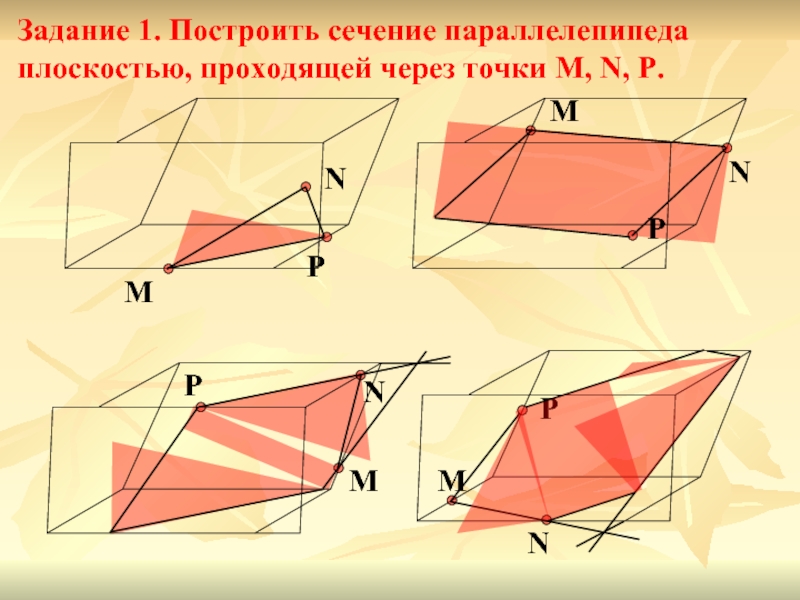
Задание 1. Построить сечение параллелепипеда плоскостью, проходящей через точки M, N,
P.
Слайд 92 блок составного урока 3х30
Срезовая работа по проверке умения строить сечения
тетраэдра и параллелепипеда плоскостью, проходящей через три заданные точки
Слайд 10
M
N
P
Вариант 1
Вариант 2
M
N
P
M
N
P
M
N
P
Задание 1. Построить сечение тетраэдра плоскостью, проходящей через точки
M, N, P.
Слайд 13Вариант 1
Вариант 2
M
N
P
M
N
P
M
N
P
M
N
P
Задание 2. Построить сечение параллелепипеда плоскостью, проходящей через
точки M, N, P.
Слайд 163 блок составного урока 3х30
Решение сложных геометрических задач с применением навыков
и умений построения сечений тетраэдра и параллелепипеда
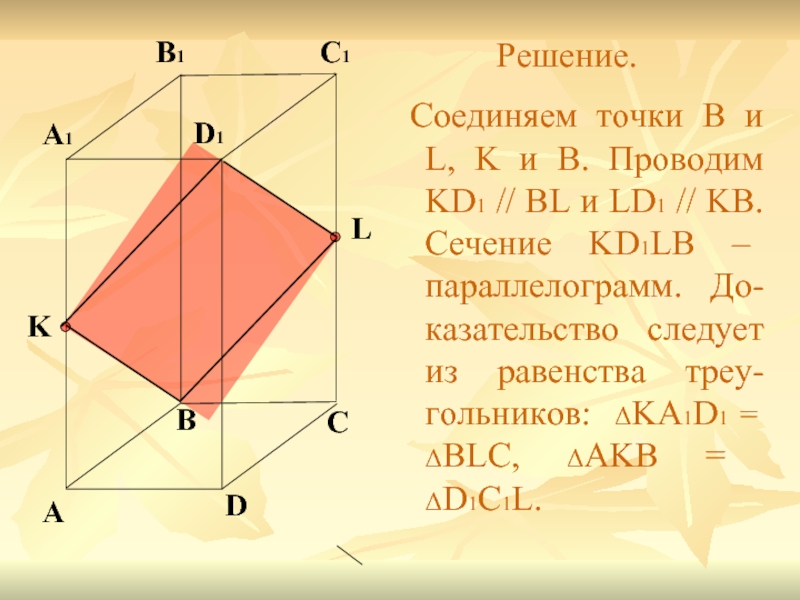
Слайд 17Задание 1. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью BKL, где K –
середина ребра AA1, а L – середина ребра СС1. Доказать, что построенное сечение – параллелограмм.
Слайд 18
A
B
C
D
A1
B1
C1
D1
K
L
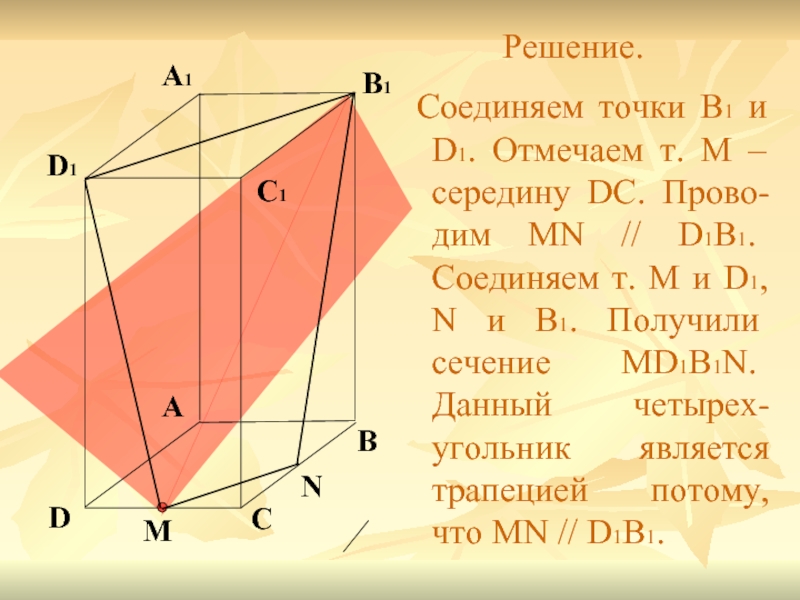
Решение.
Соединяем точки B и L, K и B. Проводим KD1
// BL и LD1 // KB. Сечение KD1LB – параллелограмм. До-казательство следует из равенства треу-гольников: ΔKA1D1 = ΔBLC, ΔAKB = ΔD1C1L.
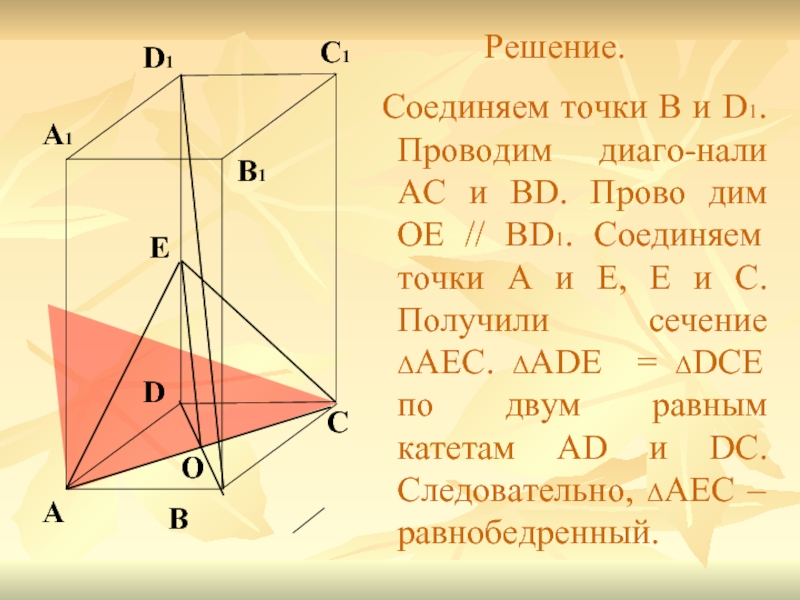
Слайд 19Задание 2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через диагональ АС
основания параллельно диагонали BD1. Доказать, что построенное сечение – равнобедренный треугольник, если основание параллелепипеда – ромб и углы ABB1 и CBB1 прямые.
Слайд 20
A
B
C
D
A1
B1
C1
D1
E
Решение.
Соединяем точки B и D1. Проводим диаго-нали AC и BD.
Прово дим OE // BD1. Соединяем точки А и Е, Е и С. Получили сечение ΔАЕС. ΔADE = ΔDCE по двум равным катетам AD и DC. Следовательно, ΔАЕС – равнобедренный.
О
Слайд 21Задание 3. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки В1
и D1 и середину ребра CD. Доказать, что построенное сечение – трапеция.
Слайд 22A
B
C
D
A1
B1
C1
D1
М
N
Решение.
Соединяем точки B1 и D1. Отмечаем т. М – середину
DC. Прово-дим MN // D1B1. Соединяем т. M и D1, N и B1. Получили сечение MD1B1N. Данный четырех-угольник является трапецией потому, что MN // D1B1.
