- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия в кубе, параллелепипеде, призме и пирамиде презентация
Содержание
- 1. Симметрия в кубе, параллелепипеде, призме и пирамиде
- 2. Симметрия – это закономерная повторяемость элементов (или частей)
- 3. Симметрия в кубе Оси симметрии в кубе:
- 4. Плоскости симметрии в кубе - плоскости, проходящие
- 5. Симметрия в параллелепипеде У прямоугольного параллелепипеда,
- 6. Симметрия в призме 1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы
- 7. 2. Плоскости симметрии: плоскость, проходящая
- 8. 3. Оси симметрии: при четном числе сторон основания
- 9. Симметрия в пирамиде Симметрия правильной пирамиды 1.
Слайд 2Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела,
при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся плоскость симметрии, ось симметрии, центр симметрии.
Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся плоскость симметрии, ось симметрии, центр симметрии.
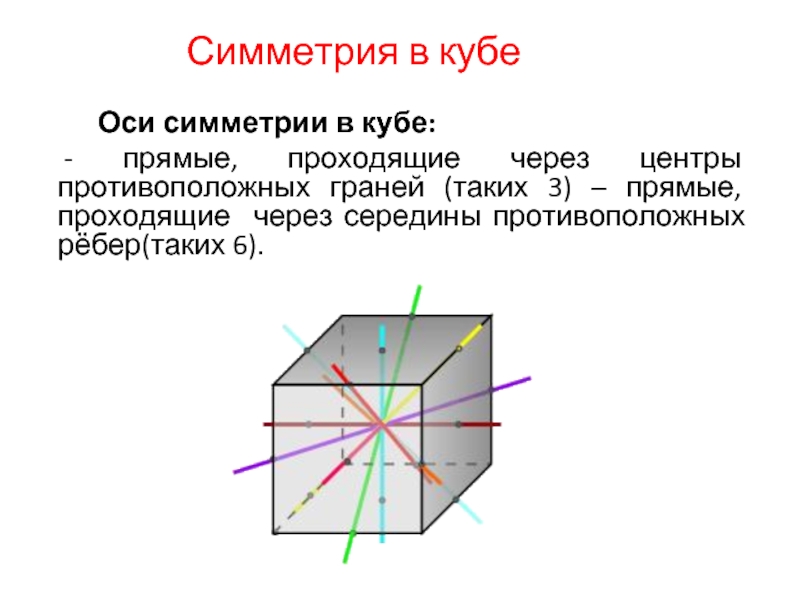
Слайд 3Симметрия в кубе
Оси симметрии в кубе:
- прямые, проходящие через центры противоположных
граней (таких 3) – прямые, проходящие через середины противоположных рёбер(таких 6).
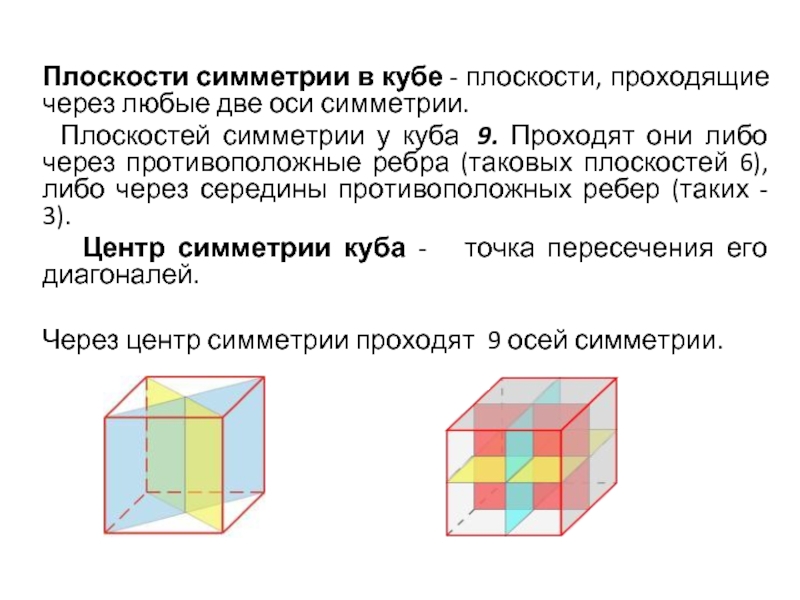
Слайд 4
Плоскости симметрии в кубе - плоскости, проходящие через любые две оси симметрии.
Плоскостей симметрии у куба 9. Проходят они либо через противоположные ребра (таковых плоскостей 6), либо через середины противоположных ребер (таких - 3).
Центр симметрии куба - точка пересечения его диагоналей.
Через центр симметрии проходят 9 осей симметрии.
Центр симметрии куба - точка пересечения его диагоналей.
Через центр симметрии проходят 9 осей симметрии.
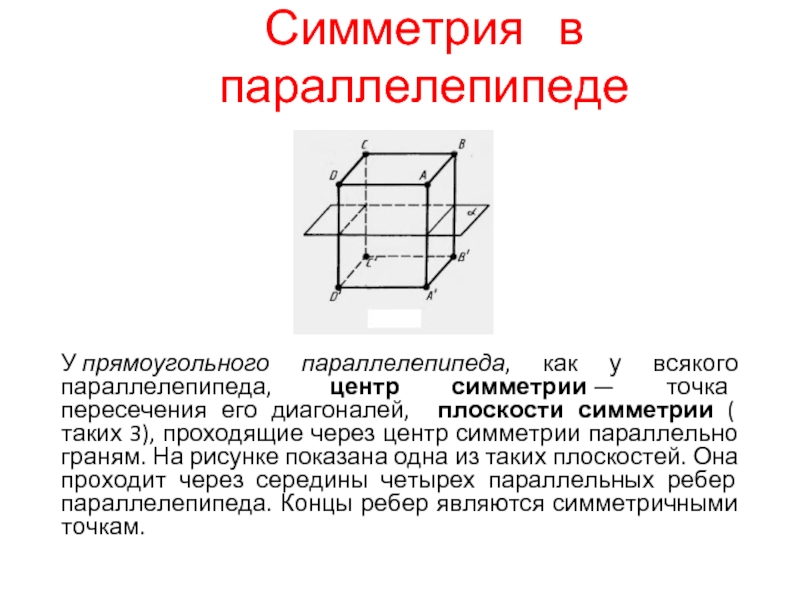
Слайд 5Симметрия в параллелепипеде
У прямоугольного параллелепипеда, как у всякого параллелепипеда, центр симметрии —
точка пересечения его диагоналей, плоскости симметрии ( таких 3), проходящие через центр симметрии параллельно граням. На рисунке показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда. Концы ребер являются симметричными точкам.
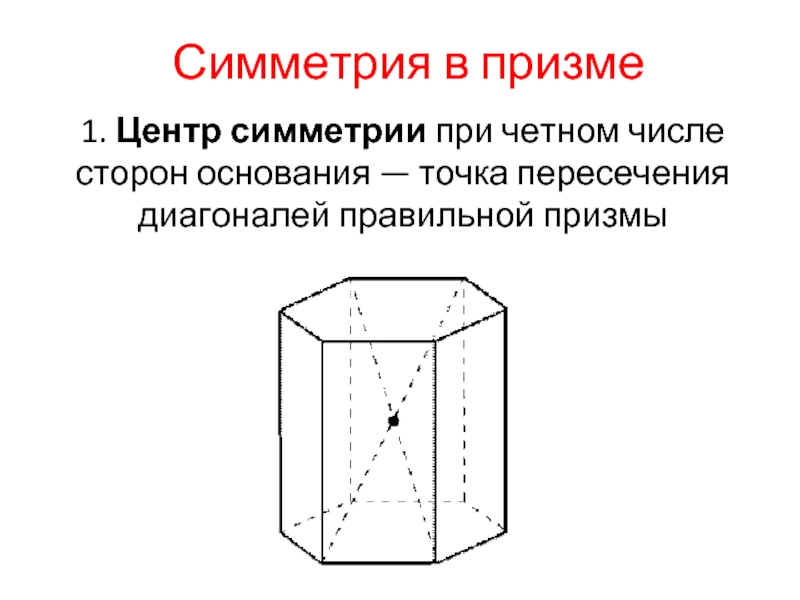
Слайд 6Симметрия в призме
1. Центр симметрии при четном числе сторон основания — точка пересечения
диагоналей правильной призмы
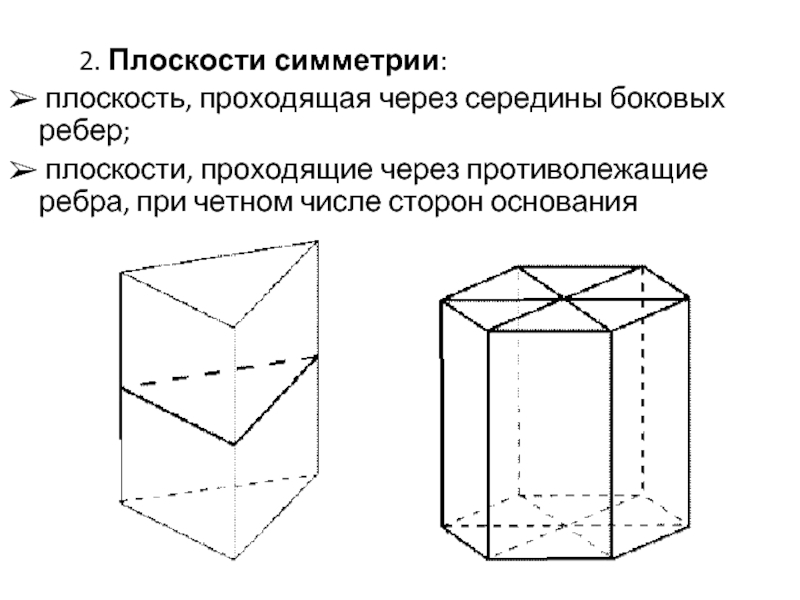
Слайд 7 2. Плоскости симметрии:
плоскость, проходящая через середины боковых ребер;
плоскости, проходящие через противолежащие ребра, при четном числе сторон основания
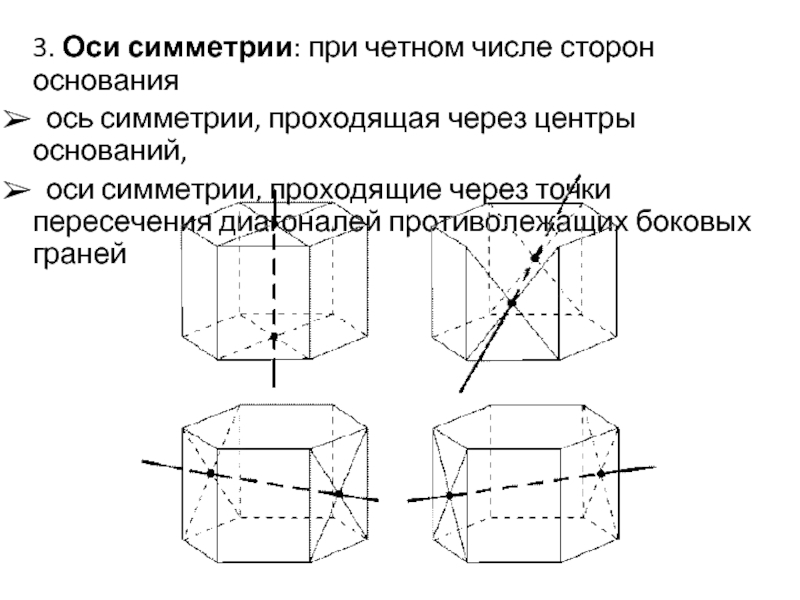
Слайд 83. Оси симметрии: при четном числе сторон основания
ось симметрии, проходящая через
центры оснований,
оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней
оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней
Слайд 9Симметрия в пирамиде
Симметрия правильной пирамиды
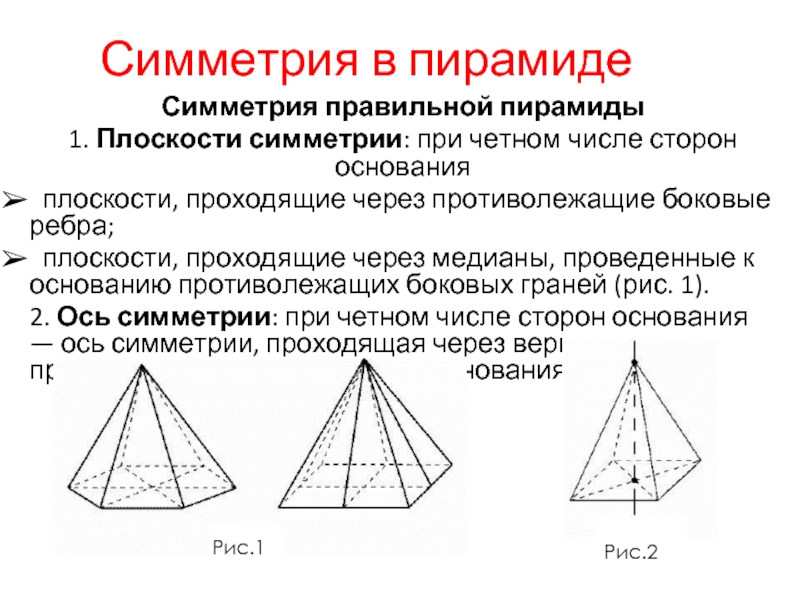
1. Плоскости симметрии: при четном числе сторон
основания
плоскости, проходящие через противолежащие боковые ребра;
плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней (рис. 1).
2. Ось симметрии: при четном числе сторон основания — ось симметрии, проходящая через вершину правильной пирамиды и центр основания (рис. 2).
плоскости, проходящие через противолежащие боковые ребра;
плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней (рис. 1).
2. Ось симметрии: при четном числе сторон основания — ось симметрии, проходящая через вершину правильной пирамиды и центр основания (рис. 2).
Рис.2
Рис.1