сведения по теории вероятностей и мат статистики
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обработка результатов измерений презентация
Содержание
- 1. Обработка результатов измерений
- 2. Случайный характер результатов измерений На результаты измерений
- 3. Пример 1 Прочность и надежность
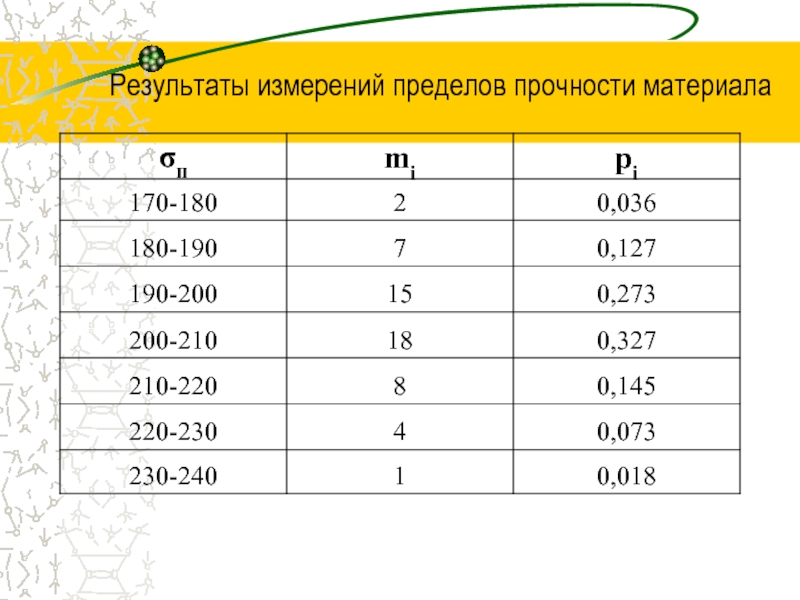
- 4. Результаты измерений пределов прочности материала
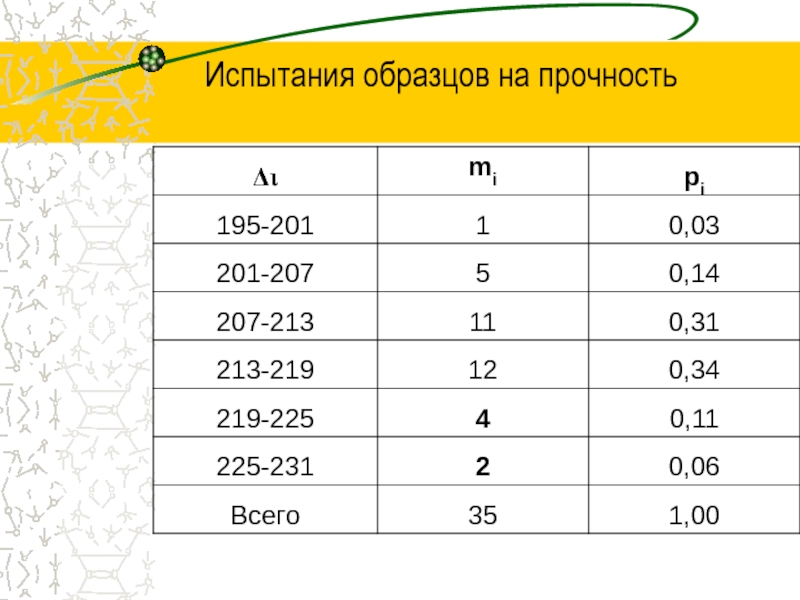
- 5. Испытания образцов на прочность
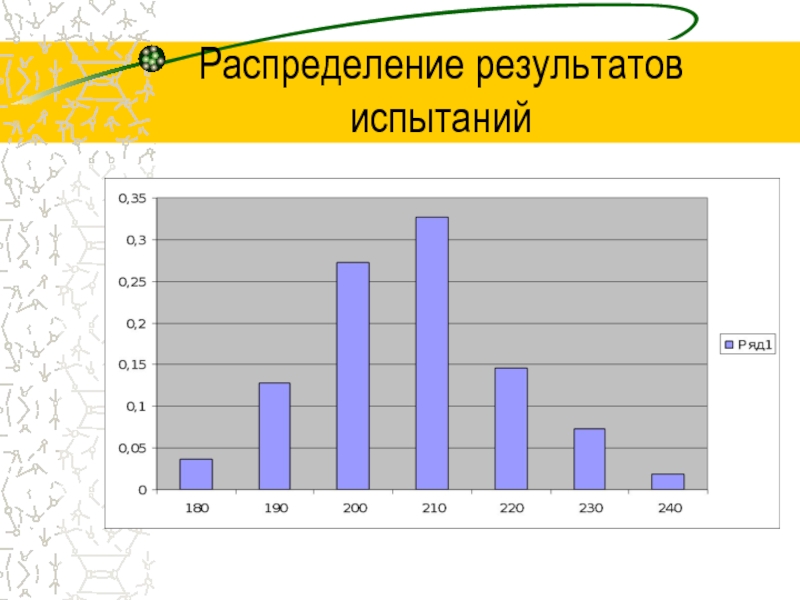
- 6. Распределение результатов испытаний
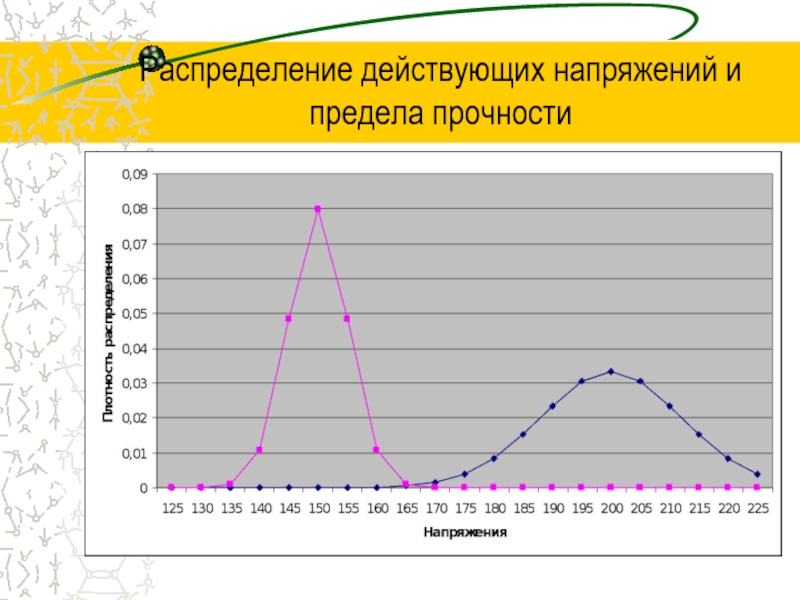
- 7. Распределение действующих напряжений и предела прочности
- 8. Критерий разрушения и запас прочности В диапазоне
- 9. Выводы из примера При решении технических задач,
- 10. Задачи обработки результатов измерений Оценка истинного
- 11. Измерения с многократными наблюдениями Отбраковка грубых
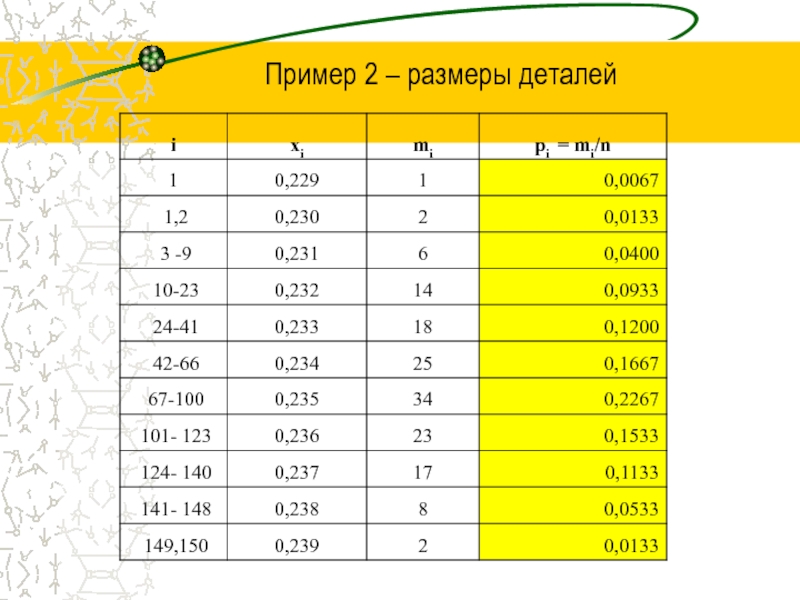
- 12. Пример 2 – размеры деталей
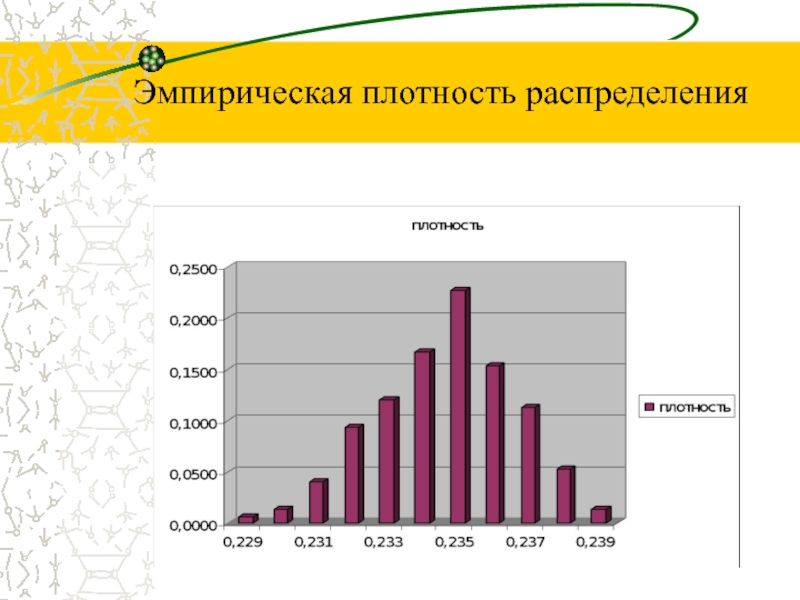
- 13. Эмпирическая плотность распределения
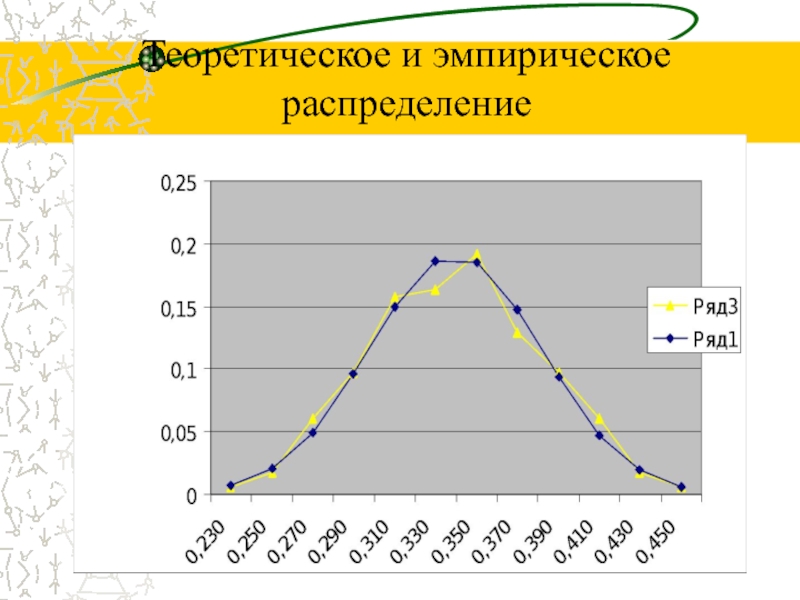
- 14. Теоретическое и эмпирическое распределение
- 15. Оценка истинного значения ФВ по результатам измерения
- 16. Оценка рассеяния результатов измерения Для оценки рассеяния
- 17. Оценка рассеяния результатов измерения при n ≥ 20
- 18. Разброс случайной величины Можно показать, что случайная
- 19. Разброс оценок среднего Величина
- 20. Разброс оценок среднего Средняя квадратичная погрешность (СКП) оценки Хr
- 21. Соотношение разброса случайной величины и ее оценки
- 22. Разброс оценок среднего Можно показать, что средний
- 23. Лекция 4. Некоторые сведения из теории вероятностей
- 24. Случайные величины Действительное переменное, которое в
- 25. Функция распределения Функцией распределения F (х)
- 26. Непрерывные СВ Случайная величина называется непрерывной, если
- 27. Плотность распределения СВ Функция f (х) называется
- 28. Интервалы и вероятности Вероятность того, что мат ожидание результата измерения лежит в интервале [-∆
- 29. Вероятность попадания в интервал При заданной плотности
- 30. Свойства распределений Нормальное и равномерное распределения
- 31. Равномерное распределение Случайная величина называется равномерно
- 32. Нормальное распределение Нормальное распределение (распределение Гаусса) если
- 33. Нормальное распределение Плотность распределения Функция распределения
- 34. Плотность нормального распределения
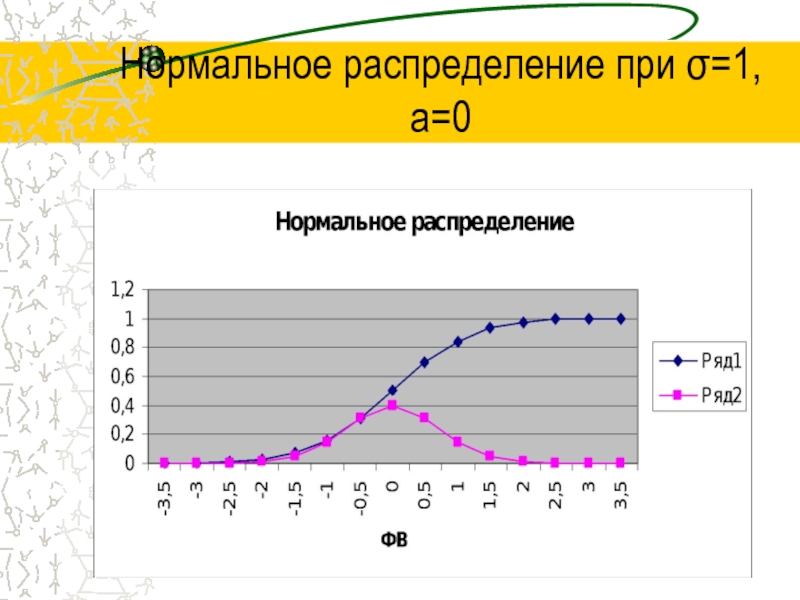
- 35. Нормальное распределение при σ=1, а=0
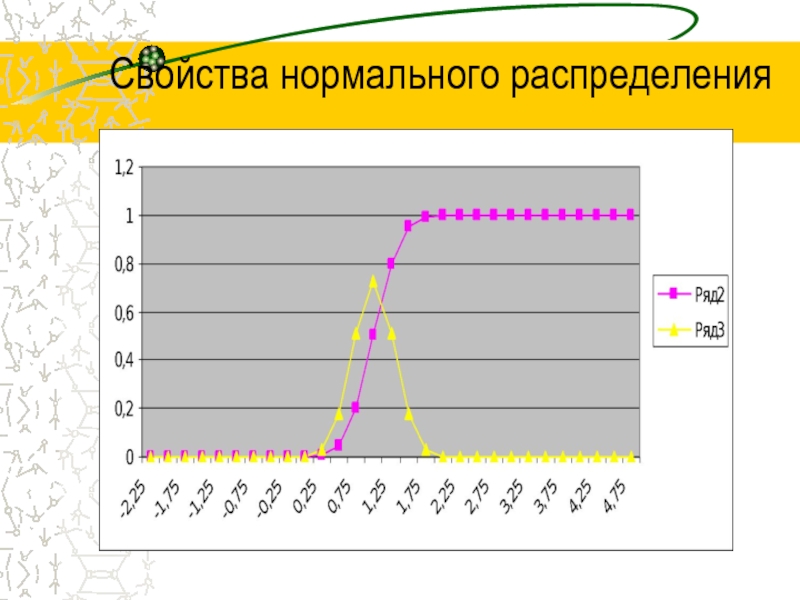
- 36. Свойства нормального распределения
- 37. Интервалы и вероятности Критические области. Квантили
- 38. Односторонняя критическая область Для односторонней критической
- 39. Квантиль Квантилью, отвечающей уровню вероятности γ, называют
- 40. Двусторонняя критическая область Для симметричной функции
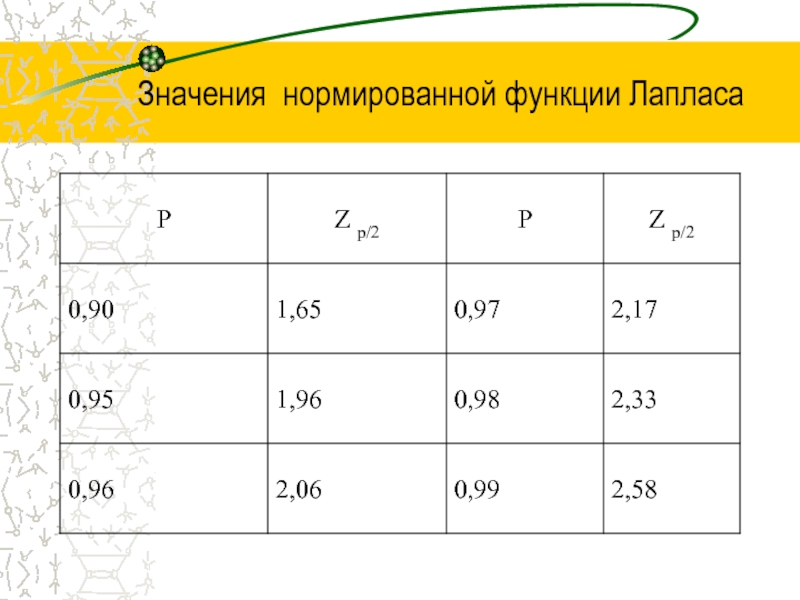
- 41. Значения нормированной функции Лапласа
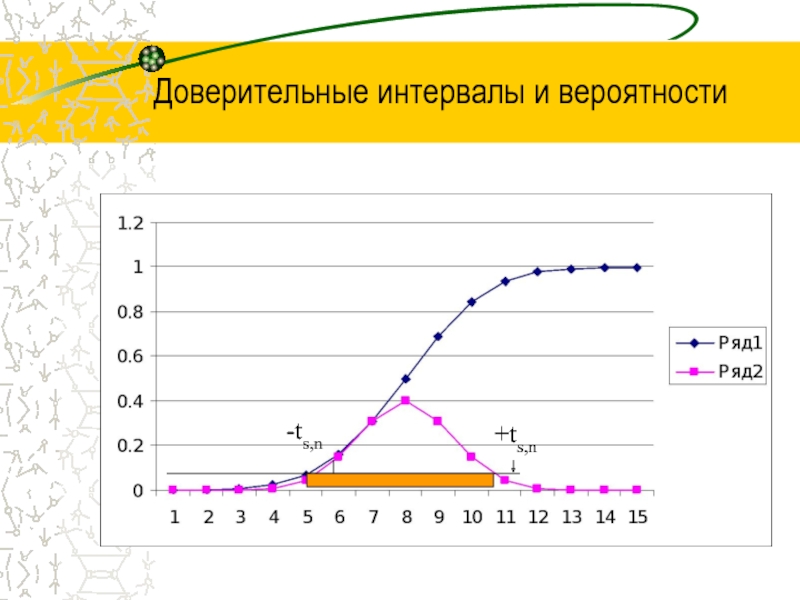
- 42. Доверительные интервалы и вероятности -ts,n +ts,n
- 43. Доверительная вероятность Вероятность того, что мат ожидание результата измерения лежит в интервале [-∆
- 44. Средний результат при малом числе измерений
- 45. Распределение Стьюдента Распределение t = X/Y с
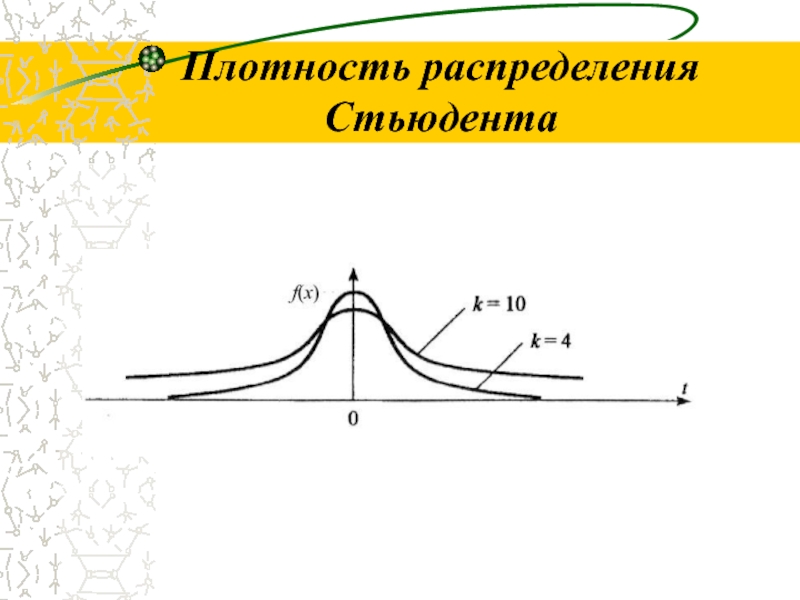
- 46. Плотность распределения Стьюдента
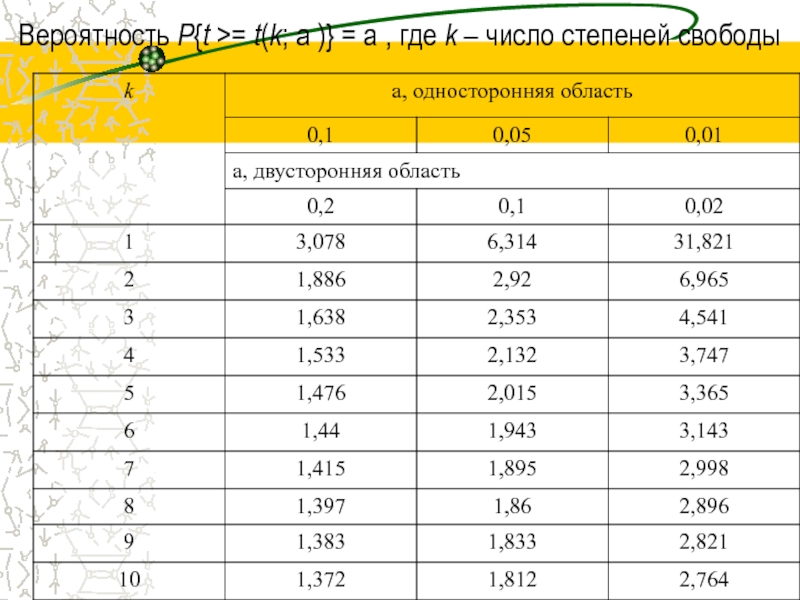
- 47. Вероятность Р{t >= t(k; a )} =
- 48. Распределение Стьюдента Таблицы распределения содержат значения для
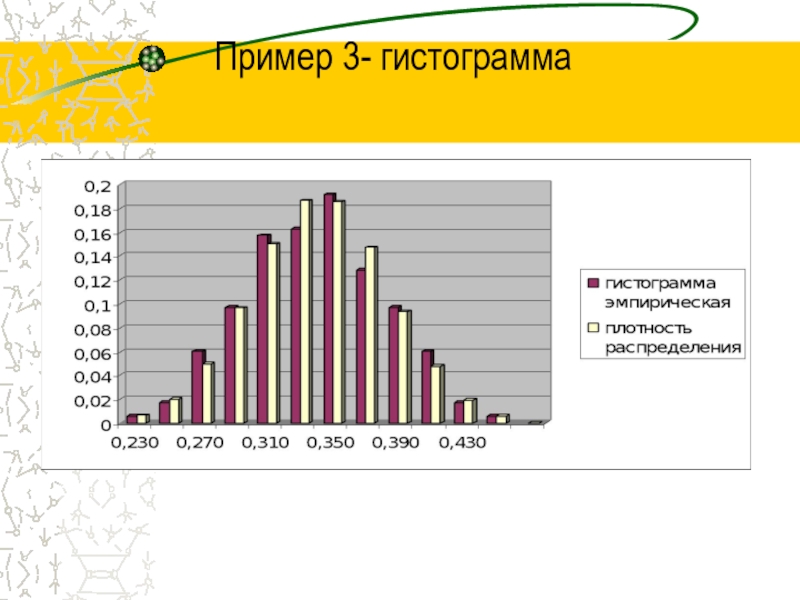
- 49. Пример 3- гистограмма
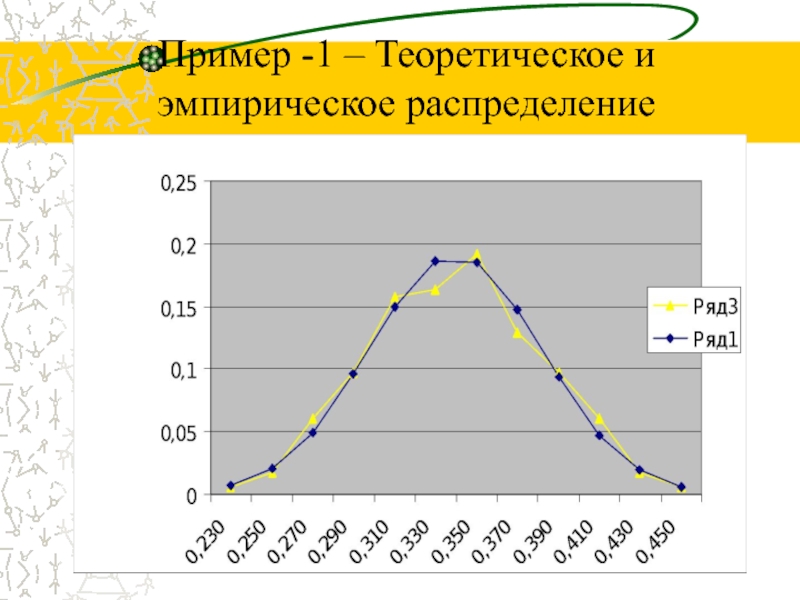
- 50. Пример -1 – Теоретическое и эмпирическое распределение
- 51. Литература Бронштейн И.Н., Семендяев К.А. Справочник по
Случайный характер результатов измерений На результаты измерений оказывают влияние большое число различных факторов, многие из которых носят случайный характер. Вследствие этого в общем случае результаты измерений являются случайными величинами и для
Слайд 1Лекция 3. Обработка результатов измерений
Проблемы и задачи обработки результатов измерений. Некоторые
Слайд 2Случайный характер результатов измерений
На результаты измерений оказывают влияние большое число различных
факторов, многие из которых носят случайный характер. Вследствие этого в общем случае результаты измерений являются случайными величинами и для их обработки требуется применение аппарата математической статистики и теории вероятностей
Слайд 8Критерий разрушения и запас прочности
В диапазоне значений 165 - 170 МПа
кривые пересекаются. Заштрихованная область соответствует событиям, когда действующие напряжения превышают предел прочности. Площадь заштрихованной области соответствует вероятности таких событий, то есть вероятности разрушения.
Слайд 9Выводы из примера
При решении технических задач, связанных с использованием результатов измерений
важно знать оценки истинных значений измеряемых величин, степень их статического разброса, границы доверительных интервалов.
Такие характеристики можно получить путем статистического анализа результатов многократных измерений
Такие характеристики можно получить путем статистического анализа результатов многократных измерений
Слайд 10Задачи обработки результатов измерений
Оценка истинного значения измеряемой величины
Оценка погрешности измерения
Оценка
доверительных интервалов и доверительной вероятности для результатов измерений
Слайд 11Измерения с многократными наблюдениями
Отбраковка грубых промахов
Оценка параметров распределения
Построение доверительных интервалов
для заданных доверительных вероятностей
Слайд 15Оценка истинного значения ФВ по результатам измерения
При многократных измерениях одного и
того же параметра в качестве оценки истинного значения используют среднее арифметическое значение
Слайд 16Оценка рассеяния результатов измерения
Для оценки рассеяния единичных результатов измерений xi в
ряду равноточных измерений одной и той же физической величины около среднего их значения используют среднеквадратичную погрешность измерений (эмпирическую) (СКП) (при n < 20)
Слайд 18Разброс случайной величины
Можно показать, что случайная величина находится с доверительной вероятностью
Р в интервале
Здесь zp – квантиль нормального распределения, зависящая от доверительной вероятности Р.
Здесь zp – квантиль нормального распределения, зависящая от доверительной вероятности Р.
Слайд 19Разброс оценок среднего
Величина , полученная в одной серии
измерений, является случайным приближением к Хr. Для оценки ее возможных отклонений от Хr (случайной погрешности среднего арифметического значения результата измерений одной и той же величины в одном ряду измерений) определяют среднюю квадратичную погрешность (СКП) оценки Хr .
Слайд 21Соотношение разброса случайной величины и ее оценки среднего
СКП из серии
измерений всегда меньше, чем в каждом отдельном измерении
,
Слайд 22Разброс оценок среднего
Можно показать, что средний результат при малом числе измерений
n находится с доверительной вероятностью Р в интервале
Здесь tp,n-1 – коэффициент Стьюдента, зависящий от степени свободы n и доверительной вероятности Р.
Здесь tp,n-1 – коэффициент Стьюдента, зависящий от степени свободы n и доверительной вероятности Р.
Слайд 23Лекция 4. Некоторые сведения из теории вероятностей и мат статистики
Некоторые сведения
из теории вероятностей и мат статистики. Статистические характеристики результатов измерений - некоторые определения.
Основные понятия теории вероятностей
Основные понятия теории вероятностей
Слайд 24Случайные величины
Действительное переменное, которое в зависимости от исхода опыта, т.
е. в зависимости от случая принимает различные значения, называется случайной величиной
Слайд 25Функция распределения
Функцией распределения F (х) случайной величины X называется функция:
Значение
функции распределения в точке х0, таким образом, равно вероятности того, что случайная величина принимает значение, меньшее х0
F(x) = P(X < x).
Слайд 26Непрерывные СВ
Случайная величина называется непрерывной, если ее функцию распределения (интегральную функцию
распределения} можно представить в виде
Слайд 27Плотность распределения СВ
Функция f (х) называется плотностью распределения. Для плотности распределения
должно выполняться условие
Слайд 28Интервалы и вероятности
Вероятность того, что мат ожидание результата измерения лежит в
интервале [-∆
P – доверительная вероятность, а интервал
- доверительный интервал.
Слайд 29Вероятность попадания в интервал
При заданной плотности вероятности, вероятность того, что случайная
величина попадает в заданный промежуток, равна
Слайд 31Равномерное распределение
Случайная величина называется равномерно распределенной на [а, b], если
ее плотность вероятности на [а, b] постоянна, а вне [а, b] равна 0
Слайд 34Плотность нормального распределения
a – математическое ожидание
σ – среднеквадратическое отклонение
σ2 -
дисперсия
Слайд 38Односторонняя критическая область
Для односторонней критической области z(a)=z1–a, т.е. критическое
значение
аргумента z(a) соответствует квантили z1–a уровня 1–a
a – уровень значимости.
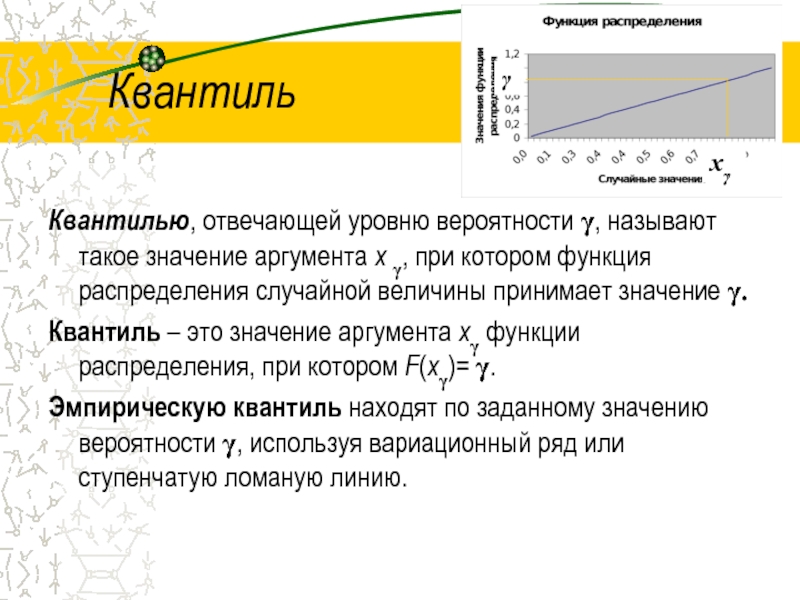
Слайд 39Квантиль
Квантилью, отвечающей уровню вероятности γ, называют такое значение аргумента x γ,
при котором функция распределения случайной величины принимает значение γ.
Квантиль – это значение аргумента xγ функции распределения, при котором F(xγ)= γ.
Эмпирическую квантиль находят по заданному значению вероятности γ, используя вариационный ряд или ступенчатую ломаную линию.
Квантиль – это значение аргумента xγ функции распределения, при котором F(xγ)= γ.
Эмпирическую квантиль находят по заданному значению вероятности γ, используя вариационный ряд или ступенчатую ломаную линию.
xγ
γ
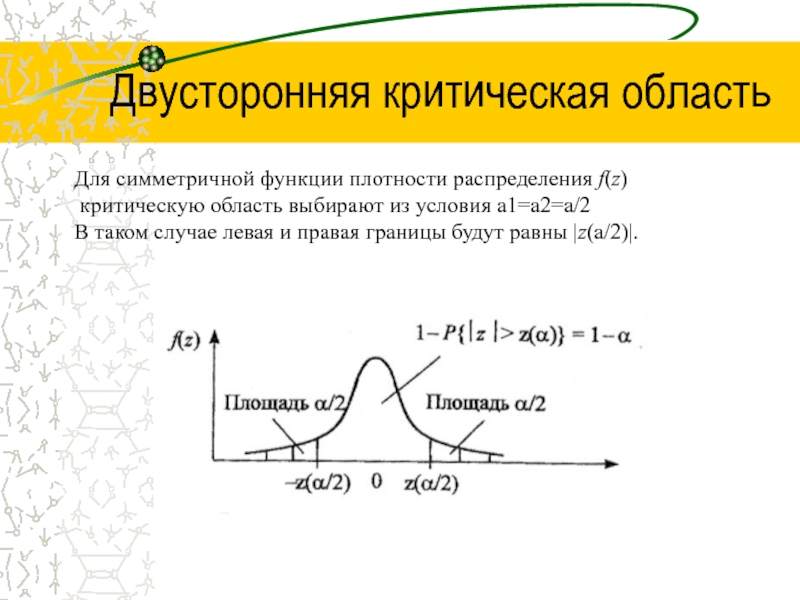
Слайд 40Двусторонняя критическая область
Для симметричной функции плотности распределения f(z)
критическую область
выбирают из условия a1=a2=a/2
В таком случае левая и правая границы будут равны |z(a/2)|.
В таком случае левая и правая границы будут равны |z(a/2)|.
Слайд 43Доверительная вероятность
Вероятность того, что мат ожидание результата измерения лежит в интервале
[-∆
Можно показать, что вероятность того, что истинная величина лежит в указанных границах равна
Где Фn(t) – функция распределения Стьюдента при степени свободы n; tp,n – квантиль распределения Стьюдента при уровне значимости p
Можно показать, что вероятность того, что истинная величина лежит в указанных границах равна
Где Фn(t) – функция распределения Стьюдента при степени свободы n; tp,n – квантиль распределения Стьюдента при уровне значимости p
Слайд 44Средний результат при малом числе измерений
Средний результат при малом числе
измерений находится с доверительной вероятностью Р в интервале
где t – квантиль распределения Стьюдента
с доверительной вероятностью Р и степенью свободы n.
Слайд 45Распределение Стьюдента
Распределение t = X/Y с независимыми X и У, где
X нормально распределено с законом N(x;0,1), а с п степенями свободы), называется t-распределением или распределением Стьюдента с п степенями свободы. Оно имеет плотность
Слайд 48Распределение Стьюдента
Таблицы распределения содержат значения для односторонней (пределы интегрирования от r(k;
a) до бесконечности)
Распределение Стьюдента применяется для описания ошибок выборки при k<30.
При k, превышающем 100, данное распределение практически соответствует нормальному, для значений k из диапазона от 30 до 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов
Распределение Стьюдента применяется для описания ошибок выборки при k<30.
При k, превышающем 100, данное распределение практически соответствует нормальному, для значений k из диапазона от 30 до 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов
Слайд 51Литература
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся
ВТУЗов. , М. , Наука, 1980
Абезгауз Г.Г. и др. Справочник по вероятностным расчетам. М., изд-во Минобороны. 1966 г.
Сергеев А.Г. и др. Метрология, стандартизация и сертификация, М.: ЛОГОС, 2003 г.
Абезгауз Г.Г. и др. Справочник по вероятностным расчетам. М., изд-во Минобороны. 1966 г.
Сергеев А.Г. и др. Метрология, стандартизация и сертификация, М.: ЛОГОС, 2003 г.
