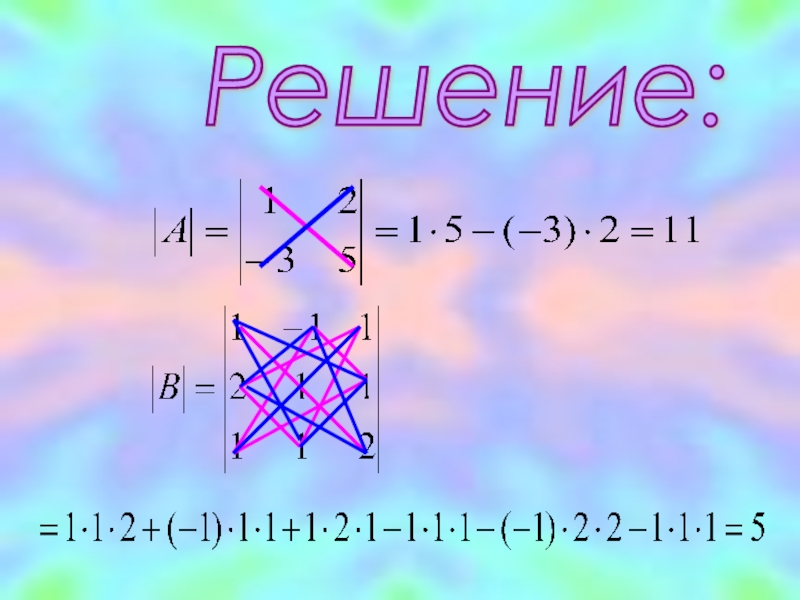- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определитель матрицы презентация
Содержание
- 1. Определитель матрицы
- 2. Определителем первого порядка матрицы называется число То есть:
- 3. Определителем второго порядка называется число, которое определяется по правилу:
- 4. Определителем третьего порядка называется число, которое определяется по правилу:
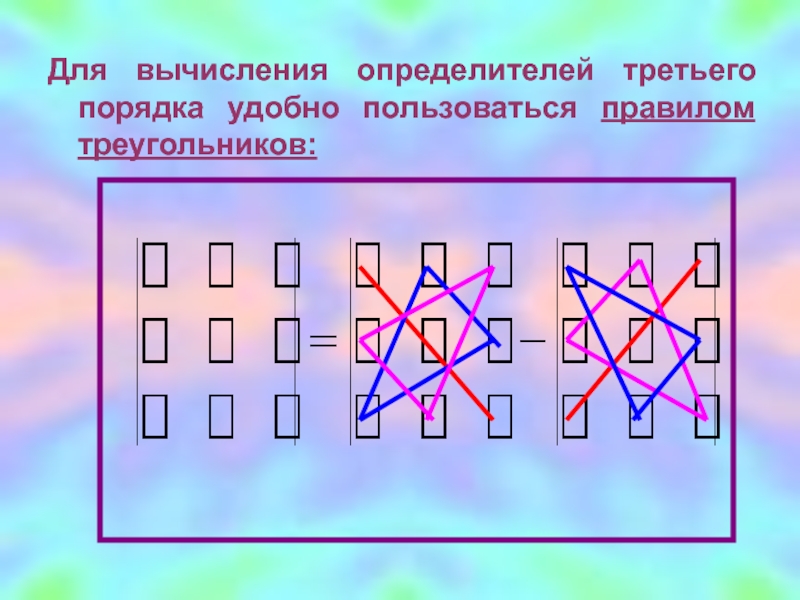
- 5. Для вычисления определителей третьего порядка удобно пользоваться правилом треугольников:
- 6. Пример. Вычислить определители матриц:
- 7. Решение:
- 8. Минором некоторого элемента определителя называется определитель,
- 9. Алгебраическим дополнением некоторого элемента определителя называется
- 10. В частности, минор элемента
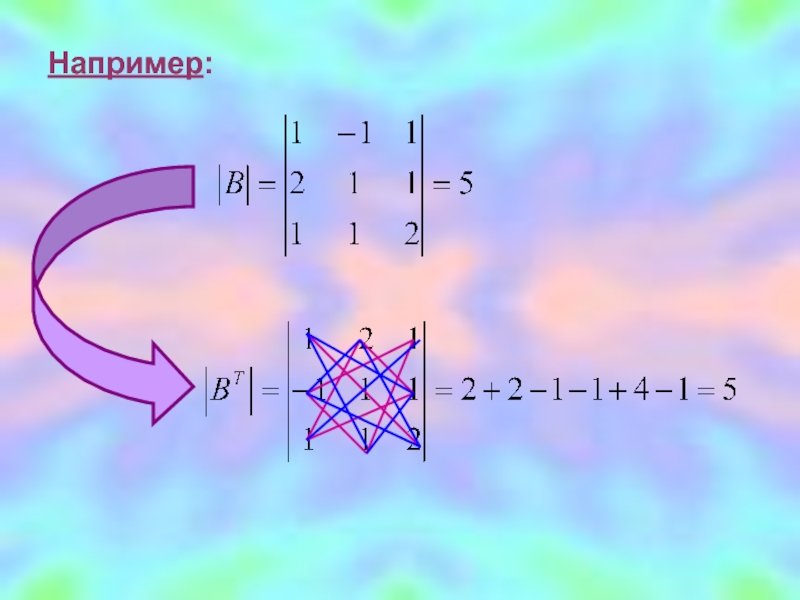
- 11. Свойства определителей 1 Определитель транспонированной матрицы равен определителю исходной матрицы.
- 12. Например:
- 13. 2 Перестановка двух строк или столбцов определителя эквивалентна умножению его на (-1).
- 14. Например: Меняем местами первую и вторую строки:
- 15. 3 Если определитель имеет две одинаковые строки или столбца, то он равен нулю.
- 16. Например:
- 17. 4 Общий множитель строки или столбца можно выносить за знак определителя.
- 18. Например: Выносим из второй строки множитель 2:
- 19. 5 Определитель не изменится, если к элементам
- 20. Например: Первую строку умножаем на 2 и складываем со второй:
- 21. 6 Определитель равен сумме произведений элементов
- 22. Пример. Вычислить определитель:
- 23. Раскладываем определитель по третьей строке: Решение: = Находим алгебраические дополнения:
- 24. Подставляем полученный результат: =
Определителем первого порядка матрицы называется число То есть:
Слайд 1Обозначается:
1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Определитель – это число,
характеризующее квадратную
матрицу.
Слайд 8Минором некоторого элемента
определителя называется определитель,
полученный из исходного
вычеркиванием строки
и столбца,
на пересечении которых стоит
данный элемент.
на пересечении которых стоит
данный элемент.
Минор элемента определителя
обозначается как
Слайд 9
Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на
(-1)S , где S – сумма номеров строки и столбца, на пересечении которых стоит данный элемент.
Слайд 10В частности, минор элемента
определителя третьего порядка найдется по правилу:
Его алгебраическое
дополнение:
Слайд 11Свойства определителей
1
Определитель транспонированной матрицы равен определителю исходной матрицы.
Слайд 195
Определитель не изменится, если
к элементам одной строки или столбца
прибавить соответственные элементы
другой
строки или столбца,
умноженные на одно и то же число.
умноженные на одно и то же число.
Слайд 216
Определитель равен сумме произведений элементов какой-либо строки или столбца на их
алгебраические дополнения:
