- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Схема Горнера презентация
Содержание
- 1. Схема Горнера
- 2. Теорема Безу , линейный множитель
- 3. Схема Горнера Коэффициенты многочлена g(x)
- 4. 1. Используя схему Горнера, разделить в кольце
- 5. 1. Используя схему Горнера, разделить в
- 6. 3 .) К=Z[x] , f(x) = 3x3
- 7. Вспомним: Тема «Классы вычетов по модулю m»
- 8. 1. Используя схему Горнера, разделить в кольце К многочлен f (x) на линейный двучлен 4.)
- 9. 1. Используя схему Горнера, разделить в кольце
- 10. 2. Используя схему Горнера, вычислить f(
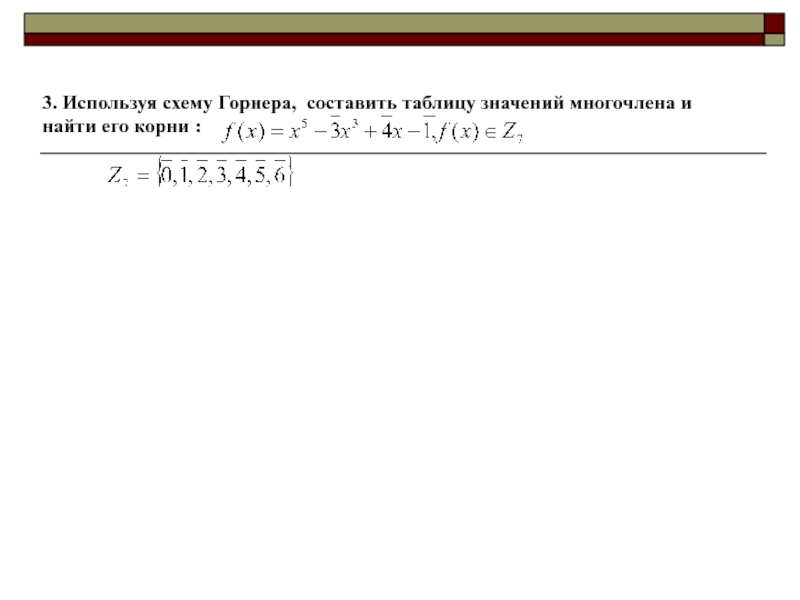
- 11. 3. Используя схему Горнера, составить таблицу значений многочлена и найти его корни :
- 12. 4. Используя схему Горнера, определить кратность корня
- 13. 4. Используя схему Горнера, определить кратность корня
- 14. 4. Используя схему Горнера, определить кратность корня
- 15. 5.При каких условиях первый из данных многочленов
- 16. 5.При каких условиях первый из данных многочленов
- 17. Задание для самостоятельной работы 1. Используя схему
- 18. Задание для самостоятельной работы 2. Используя схему
Слайд 1Теорема Безу
Схема Горнера
Спиридонова В.Л.
ГОУ СПО «Каргопольский педагогический колледж»
Отделение «Математика», 2 курс
Слайд 2Теорема Безу
,
линейный множитель
частное
остаток
Безу Этьенн
(31.3.1739-27.9.1783) французский математик
Слайд 3
Схема Горнера
Коэффициенты многочлена g(x)
Горнер Вильямc Джордж
(1786-22.9.1837) английский математик
Слайд 41. Используя схему Горнера, разделить в кольце К многочлен f (
1.) К=Z[x] , f(x)= x4 - 2x3 + 4x2 -6x + 8, =1
f(x)= (x-1)(x3 – x2 + 3x – 3)+ 5
Слайд 5
1. Используя схему Горнера, разделить в кольце К многочлен f (
2.) К=Z[x] , f(x)= x4 - 3x3 + x -1, =2
f(x)= (x - 2)(x3 + x2 - 2x - 3) - 7
Слайд 63 .) К=Z[x] , f(x) = 3x3 - 2x2 - x
f(x)= (x+2)(3x2-8x+15) - 30
1. Используя схему Горнера, разделить в кольце К многочлен f (x) на линейный двучлен
3 .) К=Z[x] , f(x) = 3x3 - 2x2 - x , = -2
Слайд 102. Используя схему Горнера, вычислить f( )
К=Z [x] ,
f(3)=5
Слайд 124. Используя схему Горнера, определить кратность корня многочлена f(x) и разложить
1.)f(x)= x5 - 5x4 + 7x3 - 2x2 + 8x2 + 4x - 8 , = 2
Слайд 134. Используя схему Горнера, определить кратность корня многочлена f(x) и разложить
2.)f(x)=x5 + 7x4 + 16x3 + 8x2 - 16x - 16, =-2
Слайд 144. Используя схему Горнера, определить кратность корня многочлена f(x) и разложить
3.)f(x)=x10 - x9 - 3x8 + 4x7 + 2x6 - 6x5 + 2x4 + 4x3 - 3x2 – x + 1, = 1 = -1
Слайд 155.При каких условиях первый из данных многочленов делится на второй ?
1.)f(x)= ax4 + 5x3 + (5 - a)x2 - ax - b , (x + 2)(x - 1)
a = 2 , b = 8
Слайд 165.При каких условиях первый из данных многочленов делится на второй ?
2.)f(x)=
a = 3 , b = -4
Слайд 17Задание для самостоятельной работы
1. Используя схему Горнера, разделить в кольце К
1) К=Z[x] , f(x)= x4- 3x3 + x -1,а= 2
2) К= Z5[x], f(x) =x4+ x3- x + 1,а= 3
3) К= С[x] , f(x)= 4x3+x2, а=-1- I
Слайд 18Задание для самостоятельной работы
2. Используя схему Горнера, определить кратность корня многочлена
1.)f(x)= x5 – 5x4 +7x3- 2x2 + 8x2 + 4x - 8 , а = 2
2.) f(x)= x5 +7x4+16x3+8x2 – 16x – 16 ,а =-2
3.)f(x)= x8 -6x7 + 13x6 - 10x5- 9x4 + 32x3 -37x2 + 20 – 4, а1 =2, а2 = 1
