- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признак параллельности прямых по равенству соответственных углов презентация
Содержание
- 1. Признак параллельности прямых по равенству соответственных углов
- 2. Если при пересечении двух прямых секущей накрест
- 3. Теорема. Если при пересечении двух прямых секущей
- 4. Задача. Прямая а параллельна прямой b. Прямая
- 5. Задача. Прямая а пересекает стороны АВ и
- 6. Задача. Прямая а пересекает стороны АВ и
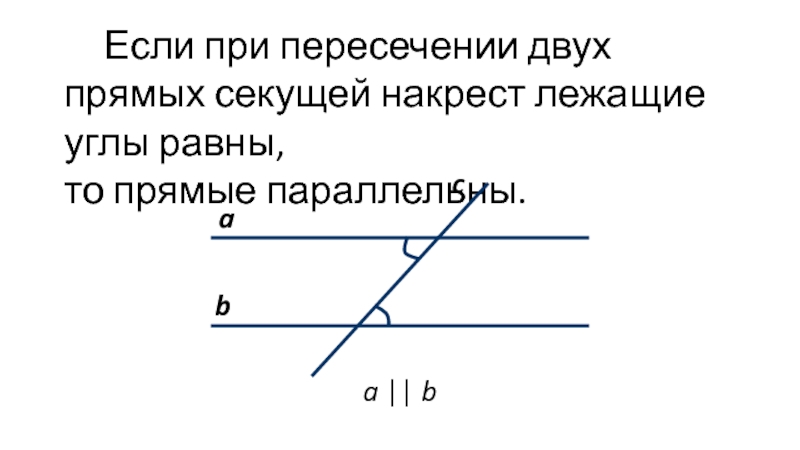
Слайд 2Если при пересечении двух прямых секущей накрест лежащие углы равны,
то
a
b
c
a || b
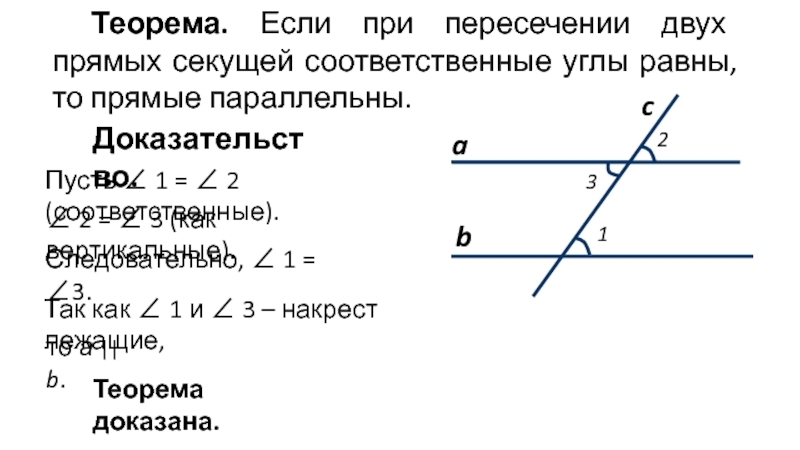
Слайд 3Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то
Доказательство.
Следовательно, ∠ 1 = ∠3.
Так как ∠ 1 и ∠ 3 – накрест лежащие,
то а || b.
Теорема доказана.
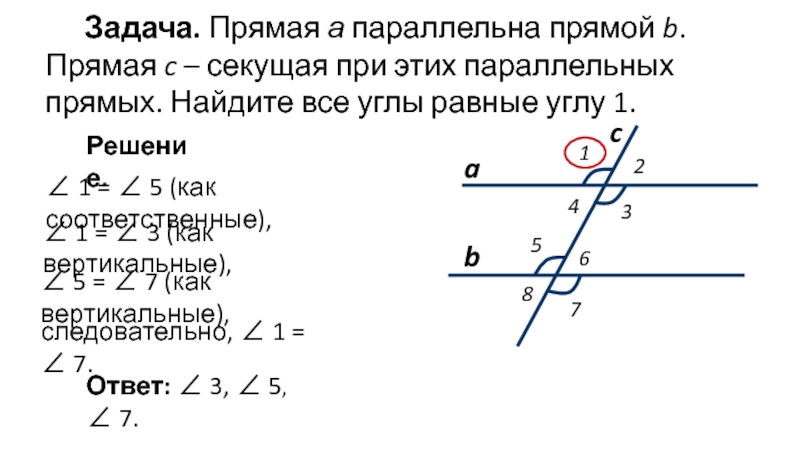
Слайд 4Задача. Прямая а параллельна прямой b. Прямая c – секущая при
Решение.
1
2
3
4
5
6
7
8
a
b
c
∠ 1 = ∠ 5 (как соответственные),
∠ 1 = ∠ 3 (как вертикальные),
∠ 5 = ∠ 7 (как вертикальные),
следовательно, ∠ 1 = ∠ 7.
Ответ: ∠ 3, ∠ 5, ∠ 7.
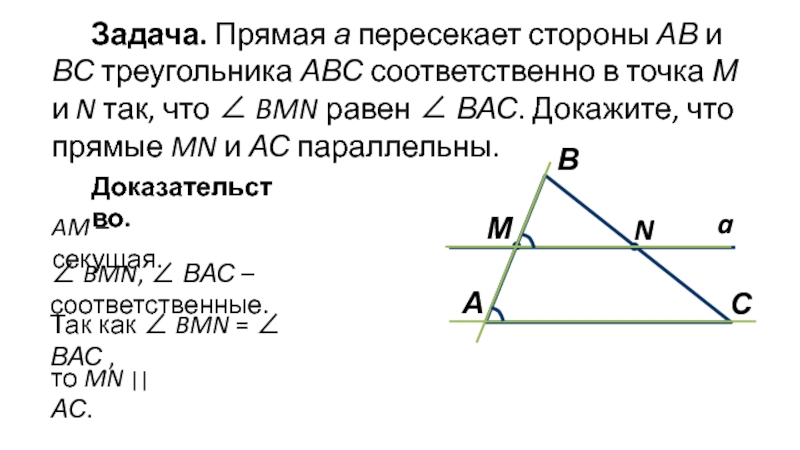
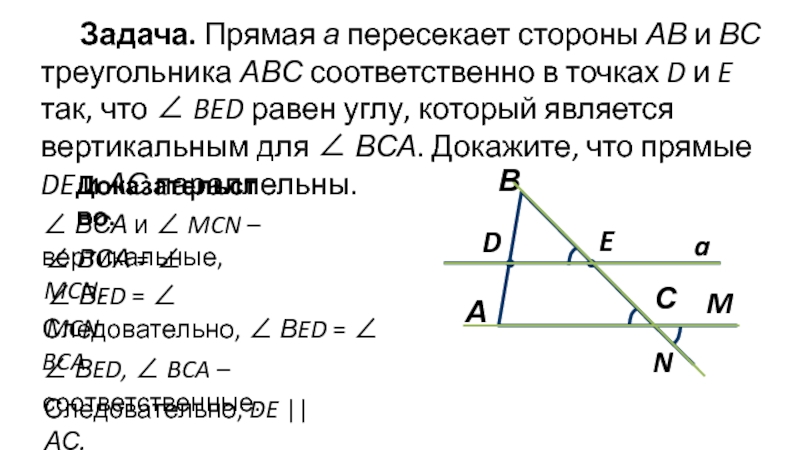
Слайд 5Задача. Прямая а пересекает стороны АВ и ВС треугольника АВС соответственно
Доказательство.
А
N
М
С
В
a
AM – секущая.
∠ BMN, ∠ ВАС – соответственные.
Так как ∠ BMN = ∠ ВАС ,
то MN || АС.
Слайд 6Задача. Прямая а пересекает стороны АВ и ВС треугольника АВС соответственно
Доказательство.
А
С
В
D
E
M
N
∠ ВСА и ∠ MCN – вертикальные,
∠ ВСА = ∠ MCN.
Следовательно, ∠ ВED = ∠ BCA.
∠ ВED, ∠ BCA – соответственные.
Следовательно, DE || АС.
a
∠ ВED = ∠ MCN.