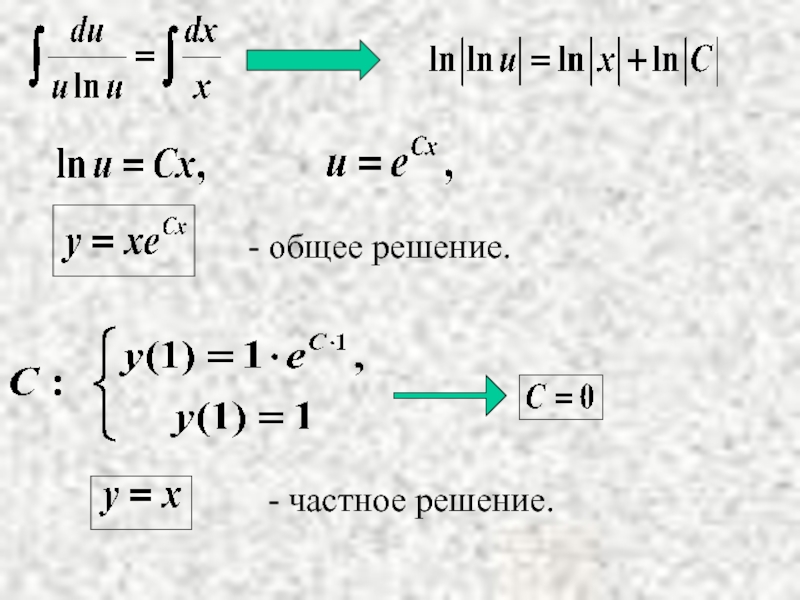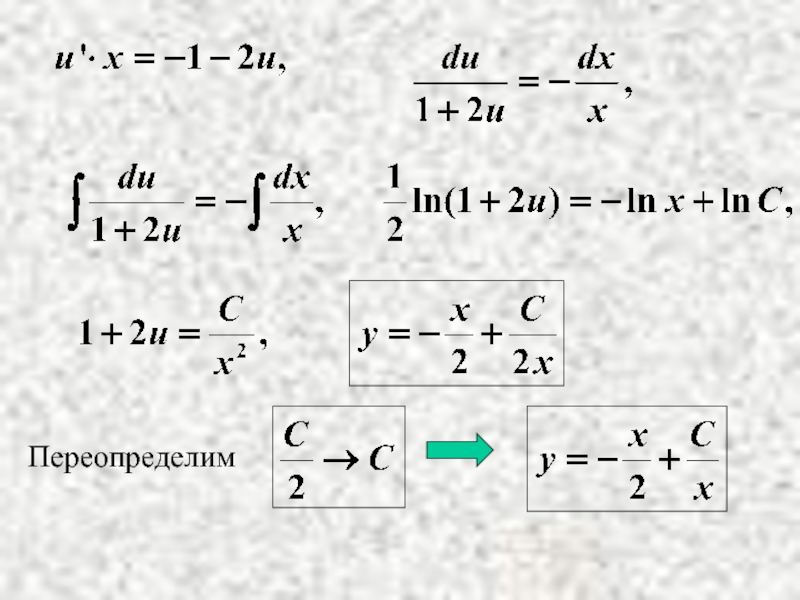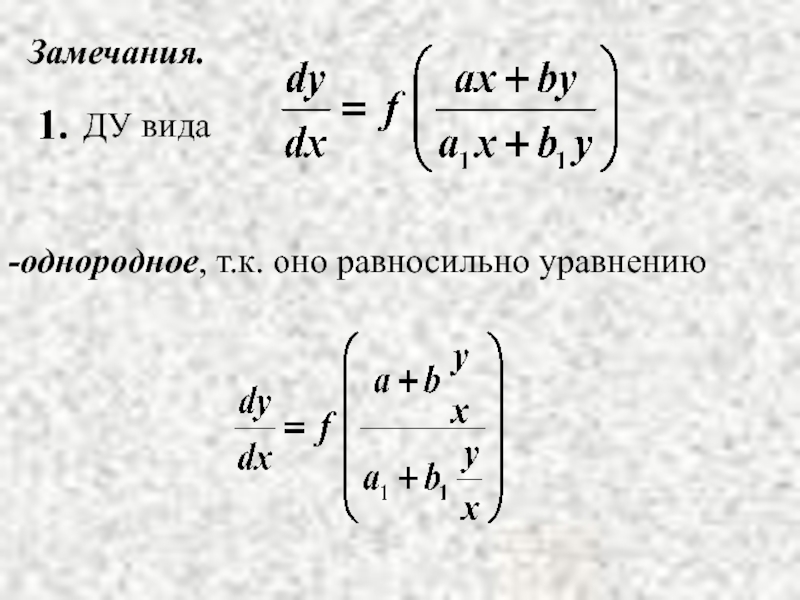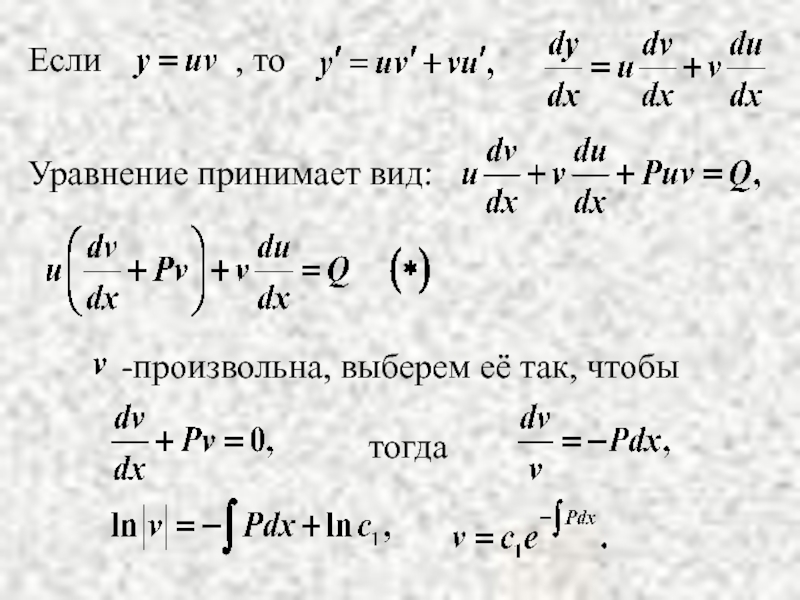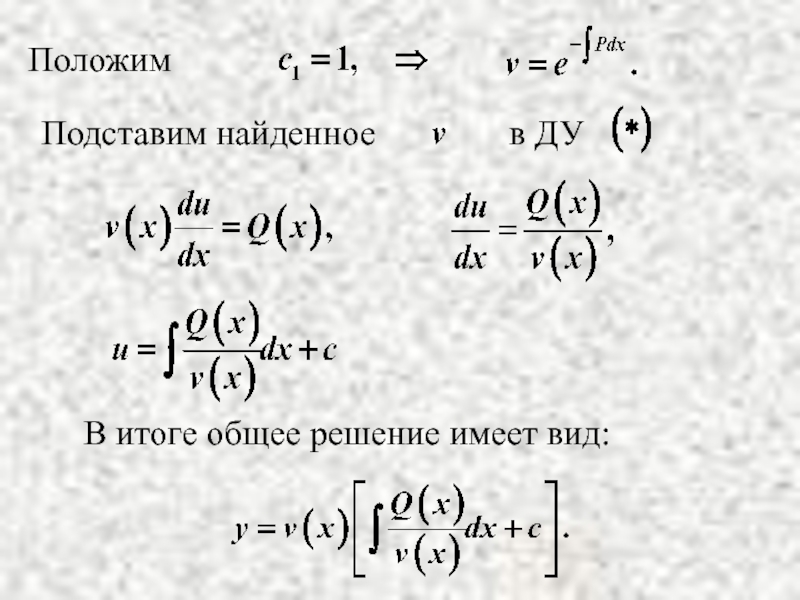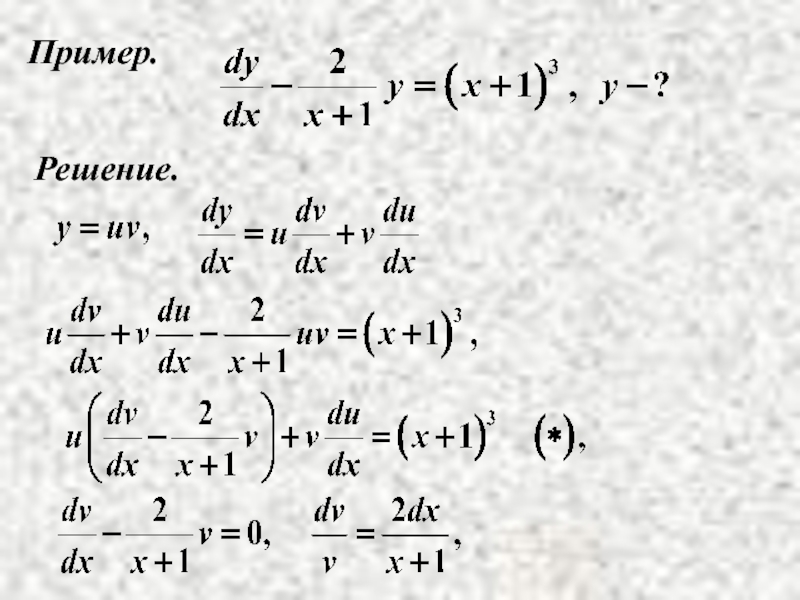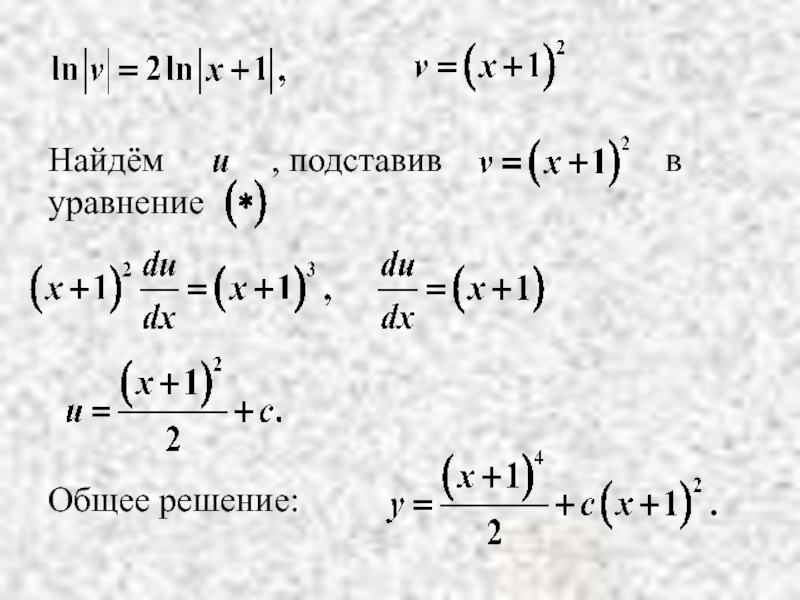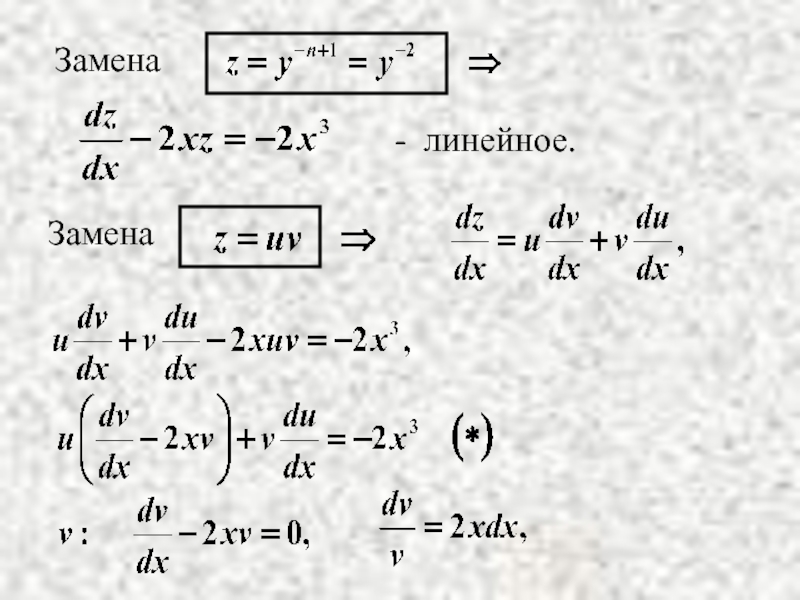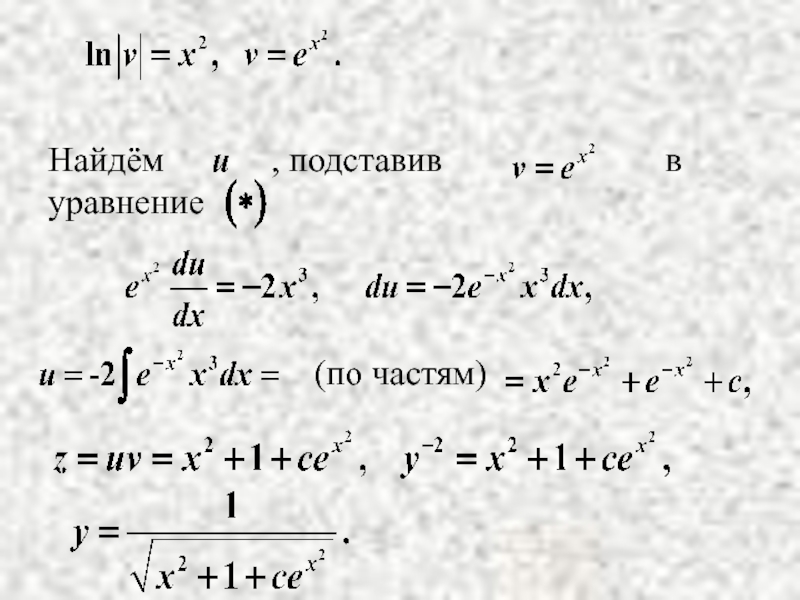- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обыкновенные дифференциальные уравнения презентация
Содержание
- 1. Обыкновенные дифференциальные уравнения
- 2. Лекция 11 Обыкновенные дифференциальные уравнения
- 3. Основной задачей теории ДУ является нахождение неизвестных функций, входящих в дифференциальные уравнения.
- 4. Примеры - ДУ 1-го порядка, -
- 5. График этой функции называется интегральной кривой.
- 7. Всякое решение, которое получается из
- 8. Пример: Решение: удовлетворяет уравнению и является общим решением.
- 9. На графике это будет однопараметрическое
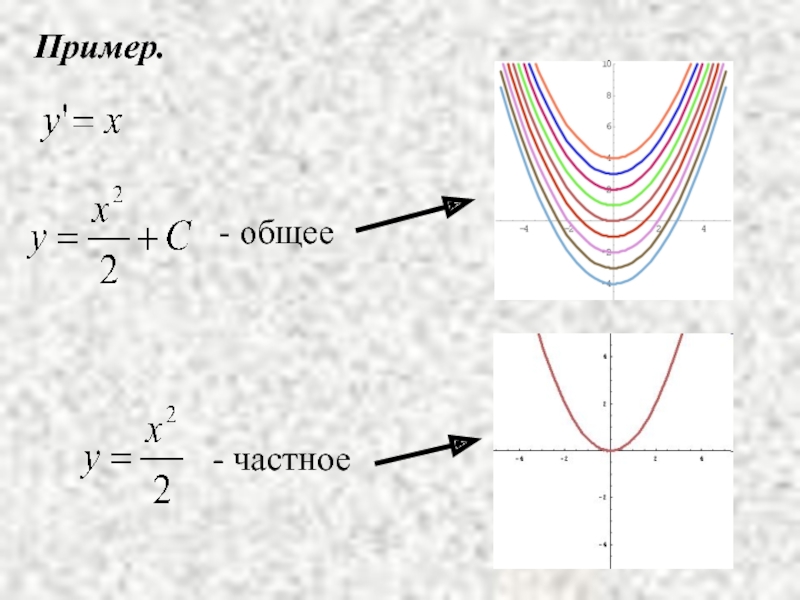
- 10. Пример. - общее - частное
- 11. Задача Коши Пусть ДУ 1-го порядка, Найти
- 12. Если
- 13. Геометрический смысл теоремы Коши. Особая точка дифференциального
- 14. Пример.
- 15. Типы ДУ первого порядка. I. ДУ с разделяющимися переменными. называется ДУ с разделяющимися переменными.
- 16. Пример 1. Решение. Общий интеграл этого уравнения:
- 17. или, представив постоянную интегрирования в логарифмической форме Пример 2. Решение.
- 18. приводятя к уравнениям с разделяющимися переменными. 2. Однородные ДУ. однородным ДУ первого порядка.
- 19. Пример 1. Решение. Дифференциальное уравнение– однородное.
- 20. - общее решение.
- 21. Пример 2. Решение. Дифференциальное уравнение– однородное.
- 23. Замечания. однородное, т.к. оно равносильно уравнению
- 24. с помощью замены:
- 25. приводит исходное ДУ к уравнению с разделяющимися переменными.
- 26. 3. Линейные ДУ первого порядка.
- 27. Уравнение принимает вид:
- 28. В итоге общее решение имеет вид:
- 29. Пример. Решение.
- 30. Общее решение:
- 31. 4. Уравнение Бернулли. называется уравнением Бернулли.
- 32. Пример: Решение. Уравнение Бернулли также решается с помощью подстановки y=u(x)v(x)
- 34. (по частям)
Слайд 3Основной задачей теории ДУ является нахождение неизвестных функций, входящих в дифференциальные
уравнения.
Слайд 4
Примеры
- ДУ 1-го порядка,
- ДУ 3-го порядка.
Порядок наивысшей производной, входящей в
уравнение, называется порядком ДУ.
Слайд 7
Всякое решение, которое получается из общего при конкретных значениях произвольных постоянных,
называется частным решением ДУ.
Слайд 9
На графике это будет однопараметрическое семейство кривых .
Общее
решение:
ДУ первого порядка называется уравнение
или
Слайд 11Задача Коши
Пусть
ДУ 1-го порядка,
Найти
решение ДУ, удовлетворяющее начальному условию.
начальное условие.
Геометрический смысл:
Слайд 13Геометрический смысл теоремы Коши.
Особая точка дифференциального уравнения – точка (х,у), в
которой нарушается единственность решения задачи Коши.
Слайд 15Типы ДУ первого порядка.
I. ДУ с разделяющимися переменными.
называется ДУ с разделяющимися
переменными.
Слайд 18приводятя к уравнениям с разделяющимися переменными.
2. Однородные ДУ.
однородным ДУ первого
порядка.