- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сечения параллелепипеда презентация
Содержание
- 1. Сечения параллелепипеда
- 2. Цель этой презентации « Сечения параллелепипеда» состоит
- 3. Цель этой презентации « Сечения параллелепипеда» состоит
- 4. D B A C M
- 5. Сечение параллелепипеда. D B A C
- 6. B Q Сечение параллелепипеда.
- 7. B Сечение параллелепипеда.
- 8. Какая грань параллельна грани АА₁В₁В? PQ||MN
- 9. Плоскость МNE пересекает грань АВСD по отрезку
- 10. B Q 3.Построить cечение параллелепипеда
- 11. Использованные ресурсы: 1. Л.С. Атанасян, В. Ф.
Слайд 1Сечения параллелепипеда.
Геометрия. 10 класс.
г. Екатеринбург.
МАОУ-гимназия №13.
Учитель математики
Анкина Тамара Степановна.
Слайд 2Цель этой презентации
« Сечения параллелепипеда» состоит в том,
чтобы помочь учащимся
алгоритм построения сечений параллелепипеда.
Она является продолжением презентации
«Сечения тетраэдра». Поэтому, если вы
забыли основные алгоритмы построения
точки пересечения прямой и плоскости и
линии пересечения плоскостей, их стоит
повторить, используя эту презентацию.
Учащимся.
Слайд 3Цель этой презентации
« Сечения параллелепипеда» состоит в том,
чтобы помочь учащимся
алгоритм построения сечений параллелепипеда.
Она является продолжением презентации
«Сечения тетраэдра». Поэтому основные алгоритмы построения точки пересечения прямой и плоскости и линии пересечения плоскостей стоит повторить, используя эту презентацию.
Учителям.
Слайд 4
D
B
A
C
M
N
P
∆ MNP – сечение.
A₁
B₁
C₁
D₁
Сечение параллелепипеда.
Многоугольник, составленный из отрезков,
по которым секущая плоскость пересекает
грани многогранника, называется сечением
многогранника.
Отрезки, из которых состоит сечение,
называются следами секущей плоскости на
гранях.
Вспомните определение сечения многогранника.
Если секущая плоскость пересекает три грани параллелепипеда, то сечением
является треугольник.
Слайд 5
Сечение параллелепипеда.
D
B
A
C
M
N
P
ЧетырёхугольникMNQP –сечение.
C₁
D₁
B₁
A₁
Q
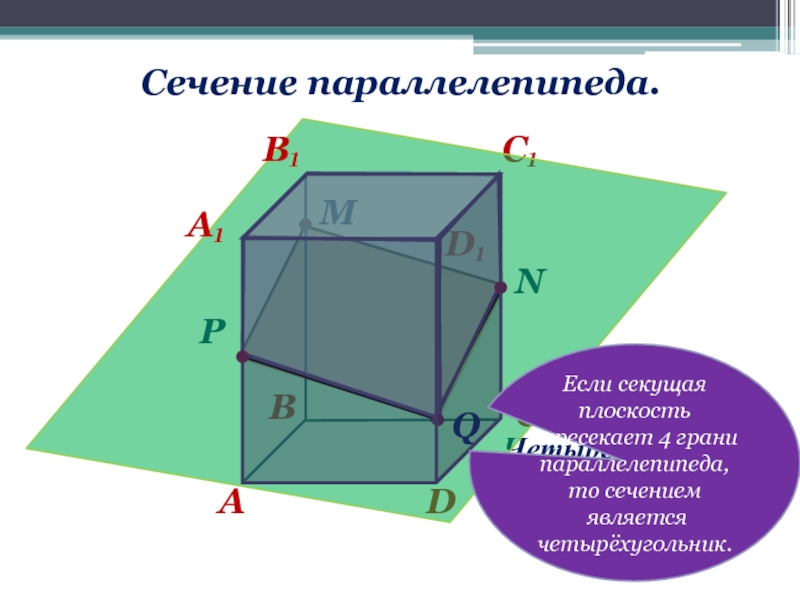
Если секущая плоскость пересекает 4 грани параллелепипеда, то сечением
является четырёхугольник.
Слайд 6B
Q
Сечение параллелепипеда.
D
A
C
C₁
B₁
A₁
P
D₁
N
М
R
Пятиугольник
MNPQR–сечение.
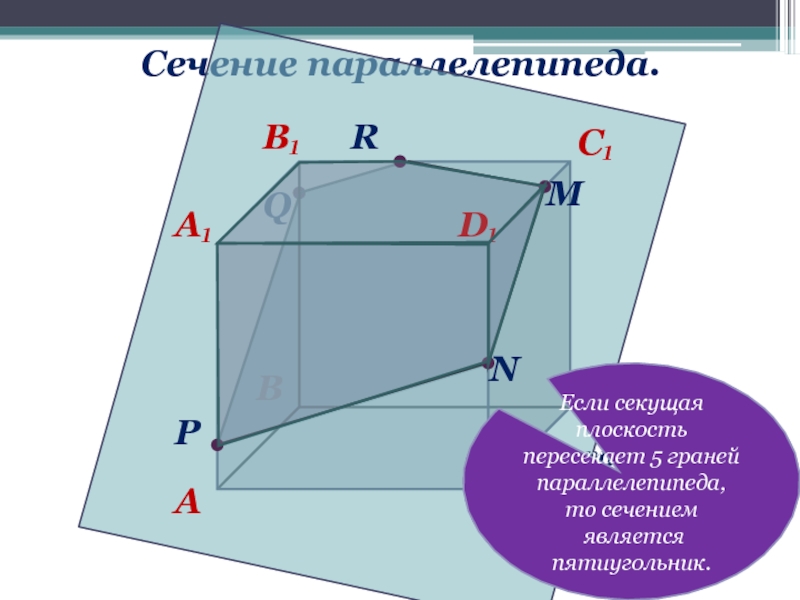
Если секущая плоскость пересекает 5 граней параллелепипеда, то сечением
является пятиугольник.
Слайд 7B
Сечение параллелепипеда.
A
C
C₁
B₁
A₁
P
N
М
R
Шестиугольник
MNPQRS–сечение.
S
Q
D
D₁
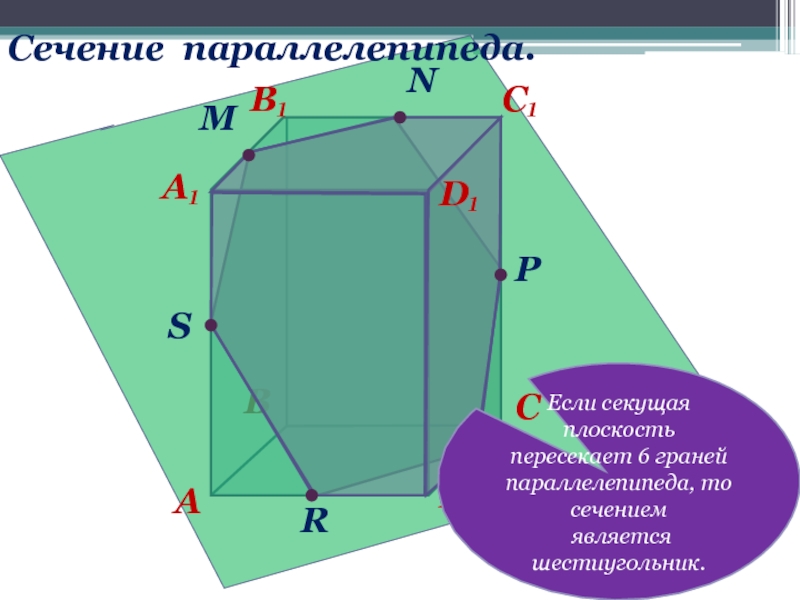
Если секущая плоскость пересекает 6 граней параллелепипеда, то сечением
является шестиугольник.
Слайд 8Какая грань параллельна грани АА₁В₁В?
PQ||MN
N
В
1.Построить сечение параллелепипеда плоскостью МNP.
A
C
C₁
B₁
A₁
P
М
D
D₁
Q
Продолжите утверждение...
Если
пересечены третьей плоскостью, то……….
……………………………………………………………………….
линии пересечения параллельны
Как должны быть расположены следы секущей плоскости в параллельных гранях?
ЧетырёхугольникMNQP –сечение.
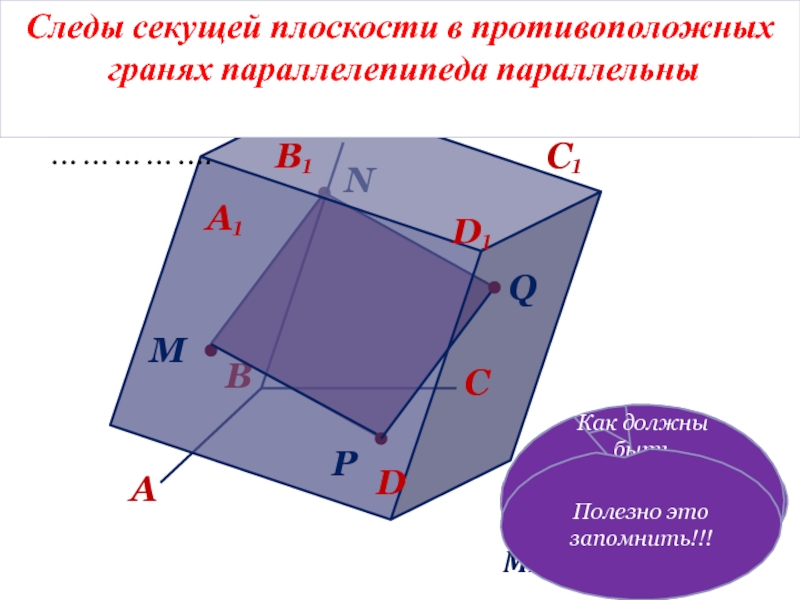
Следы секущей плоскости в противоположных
гранях параллелепипеда параллельны
Полезно это запомнить!!!
Слайд 9Плоскость МNE пересекает грань АВСD по отрезку QP
7) (MNЕ) (ABB₁)=RS
(ABB₁)||(DD₁C₁)
RS||NP.
C
Е
P
N
2.Построить cечение параллелепипеда, плоскостью МNE, (E (ABC)) .
A
C₁
B₁
М
S
Q
D
D₁
B
F
A₁
R
Шестиугольник
MNPQRS–сечение.
1) (MNЕ) (ВВ₁С₁)=MN.
2) MN (AВС)=F.
3) (MNE) (AВС)=FE.
4) (MNE) СD=P,
(MNE) AD=Q,
5) (MNЕ) (DD₁С₁)=NP.
(MNE) (AВС)=QP.
6) (MNЕ) (ADD₁)=QR
(MNЕ) (BB₁C₁)=MN
(ADD₁)||(BB₁C₁)
QR||MN.
8) (MNЕ) (A₁B₁С₁)=SM.
Точка Е лежит в грани АВСD, а прямая МN-в плоскости грани ВВ₁С₁С
Точка Е лежит в грани АВСD, а прямая МN-в плоскости грани ВВ₁С₁С
Построим точку пересечения прямой МN и плоскости грани АВСD
Грани BB₁C₁C и AA₁D₁D параллельны, значит след плоскости МNЕ в грани AA₁D₁D параллелен МN
Грани BB₁А₁Аи СС₁D₁D параллельны, значит след плоскости МNЕ в грани ВВ₁А₁А параллелен NР
Грани BB₁А₁Аи СС₁D₁D параллельны, значит след плоскости МNЕ в грани ВВ₁А₁А параллелен NР
Слайд 10
B
Q
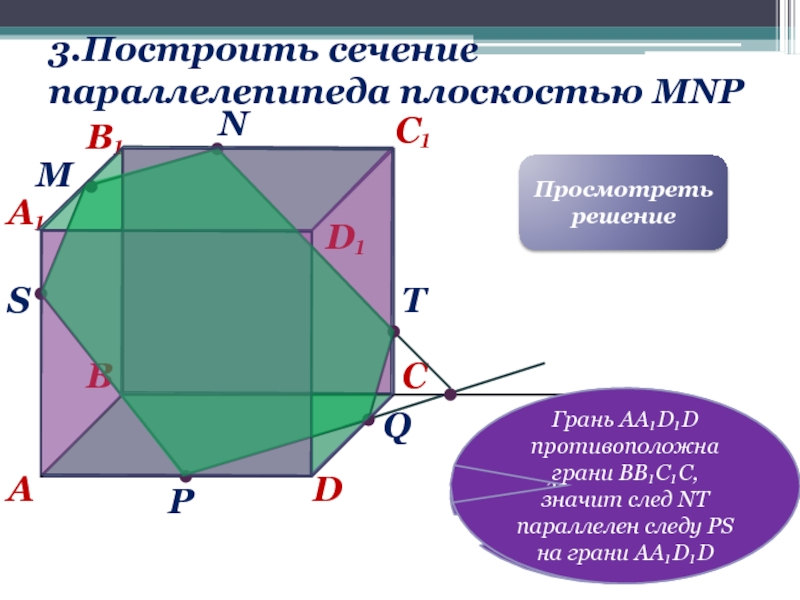
3.Построить cечение параллелепипеда плоскостью MNP
D
A
C
C₁
B₁
A₁
P
D₁
N
М
T
Шестиугольник
MNTQPS-искомое сечение.
След секущей плоскости на грани АВСD параллелен её следу MN на грани A₁B₁C₁D₁.
S
Просмотреть решение
Построим точку пересечения прямой PQ с плоскостью грани ВB₁C₁С и проведём прямую через эту точку и точку N
Грань AA₁D₁D противоположна грани ВB₁C₁С, значит след NТ параллелен следу PS на грани AA₁D₁D
Слайд 11Использованные ресурсы:
1. Л.С. Атанасян, В. Ф. Бутузов и др. Геометрия 10-11
2.Б.Г. Зив, В.М. Мейлер, А. Г. Баханский
Задачи по геометрии 7-11