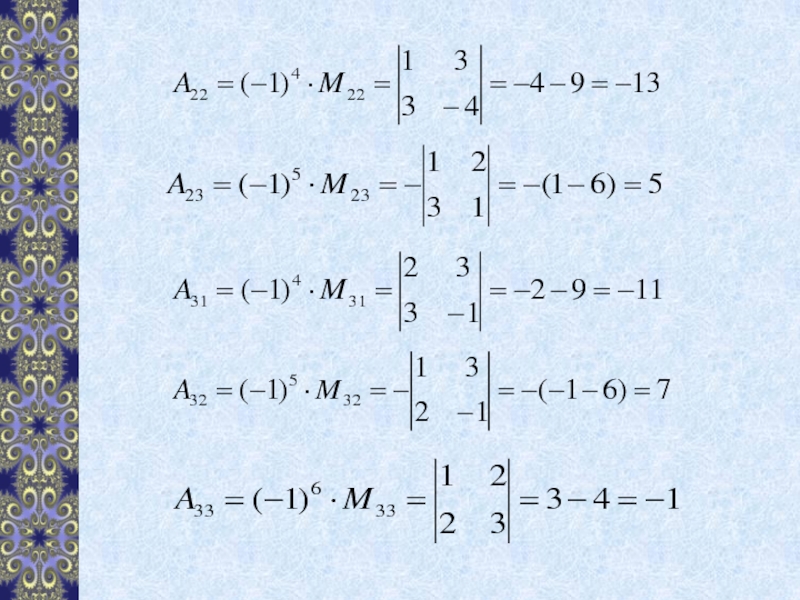1. МЕТОД ГАУССА
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение систем линейных уравнений презентация
Содержание
- 1. Решение систем линейных уравнений
- 2. Дана система из трех уравнений: Матрица системы
- 3. Исключим переменную x1 из всех уравнений, кроме
- 4. Теперь исключим переменную x2 из третьего
- 5. Запишем полученную систему уравнений: Последовательно находим: Ответ:
- 6. 2. МЕТОД КРАМЕРА Пусть дана система (1).
- 7. Пусть ΔJ – определитель матрицы, полученной из
- 8. формулы Крамера
- 9. Решим систему из предыдущего примера. Матрица системы имеет вид: Находим ее определитель:
- 10. Найдем определители Δ1 , Δ2 , Δ3 :
- 11. Используем формулы Крамера: Ответ:
- 12. Замечание: Если Δ=0 при том, что хотя
- 13. 3. МЕТОД ОБРАТНОЙ МАТРИЦЫ Пусть дана система
- 14. Тогда решением матричного уравнения будет матрица-столбец Х: Проверяем:
- 15. Решим систему из предыдущего примера. Матрица системы
- 16. Находим алгебраические дополнения для каждого элемента матрицы А :
- 18. Составляем матрицу из найденных алгебраических дополнений: Транспонируем ее и делим на определитель. Получаем обратную матрицу:
- 19. Находим решение системы уравнений: Ответ:
Слайд 1Этот метод заключается в последовательном исключении переменных из системы уравнений.
2.2.
Слайд 2Дана система из трех уравнений:
Матрица системы будет иметь вид:
Если включить в
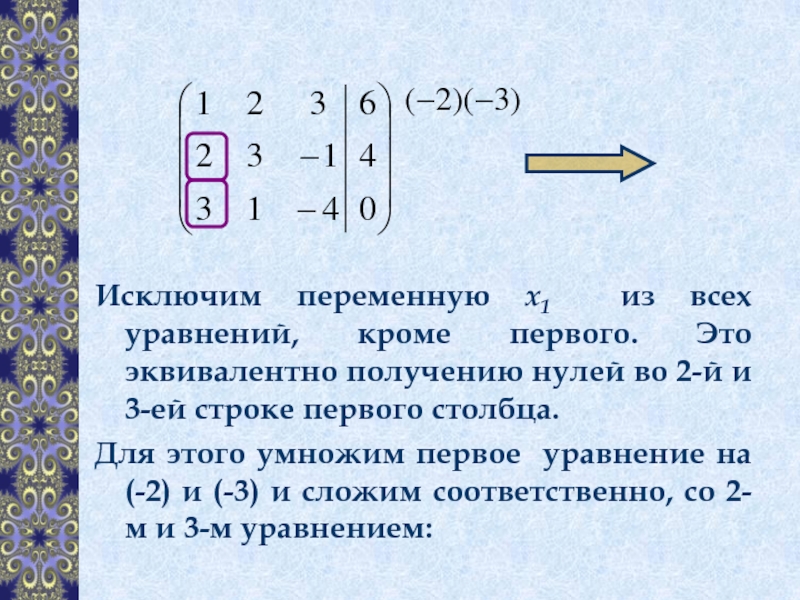
Слайд 3Исключим переменную x1 из всех уравнений, кроме первого. Это эквивалентно получению
Для этого умножим первое уравнение на (-2) и (-3) и сложим соответственно, со 2-м и 3-м уравнением:
Слайд 4
Теперь исключим переменную x2 из третьего уравнения (получим ноль в 3-ей
Для этого умножим 2-е уравнение на (-5) и сложим его с третьим:
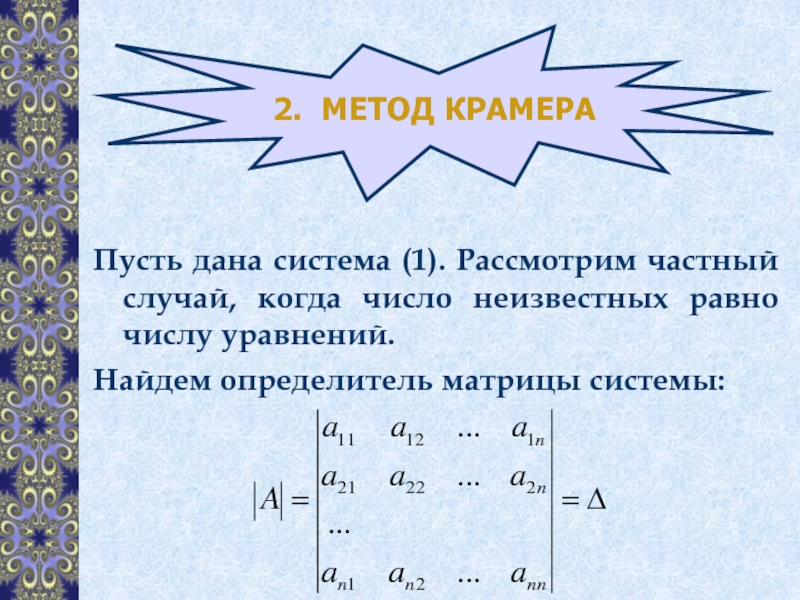
Слайд 62. МЕТОД КРАМЕРА
Пусть дана система (1). Рассмотрим частный случай, когда число
Найдем определитель матрицы системы:
Слайд 7Пусть ΔJ – определитель матрицы, полученной из матрицы А заменой j–го
Тогда, если определитель матрицы системы не равен 0, то система уравнений (1) имеет единственное решение, которое определяется по формулам:
Слайд 12Замечание:
Если Δ=0 при том, что хотя бы один
из определителей ΔJ не
то система (1) несовместна.
Если Δ=0 и все ΔJ тоже равны нулю,
то система неопределенная, так как
она имеет бесконечное множество
решений.
Слайд 133. МЕТОД ОБРАТНОЙ МАТРИЦЫ
Пусть дана система (1). Снова рассмотрим случай, когда
В матричной форме система имеет вид:
Пусть существует обратная матрица А-1 к матрице системы А.
Слайд 15Решим систему из предыдущего примера.
Матрица системы и столбец свободных членов
Найдем обратную матрицу А-1 :
Ранее был найден определитель матрицы А: