Практикум №4 по решению
планиметрических задач
( базового уровня)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение планиметрических задач базового уровня. (Практикум 4. ЕГЭ 2016) презентация
Содержание
- 1. Решение планиметрических задач базового уровня. (Практикум 4. ЕГЭ 2016)
- 2. Задания №15 базового уровня
- 3. Содержание Задача №1
- 4. Вспомним Sin A = cos B
- 5. Задача №1 В треугольнике АВС угол С равен 90°,
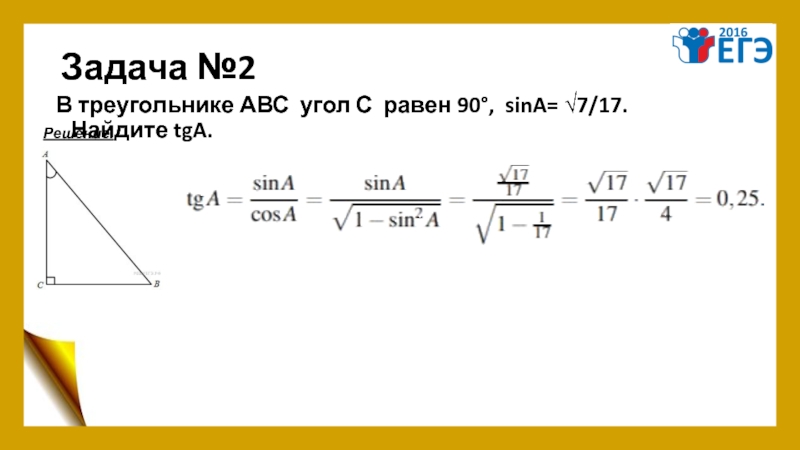
- 6. Задача №2 В треугольнике АВС угол С равен 90°, sinA= √7/17. Найдите tgA. Решение.
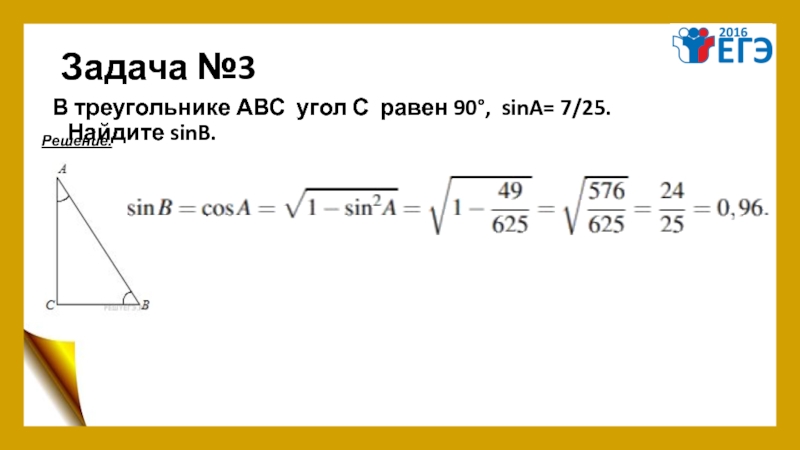
- 7. Задача №3 В треугольнике АВС угол С равен 90°, sinA= 7/25. Найдите sinB. Решение.
- 8. Задача №4 В треугольнике АВС угол С равен 90°,
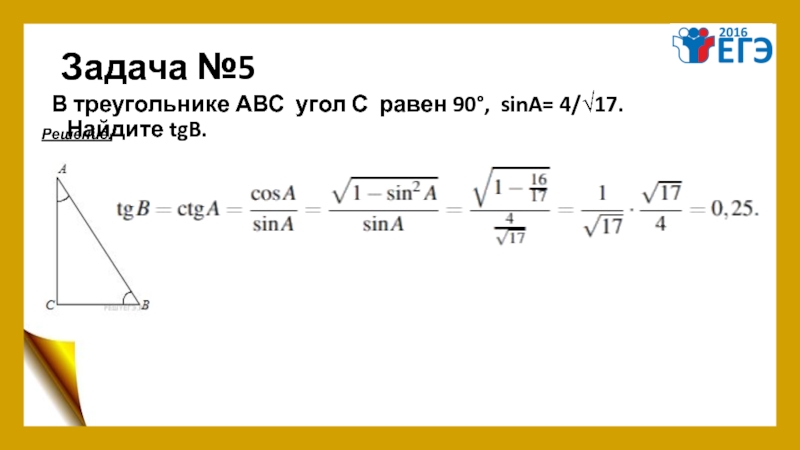
- 9. Задача №5 В треугольнике АВС угол С равен 90°, sinA= 4/√17. Найдите tgB. Решение.
- 10. Задача №6 В треугольнике АВС угол С равен 90°, tgA= 7/24. Найдите sinA. Решение.
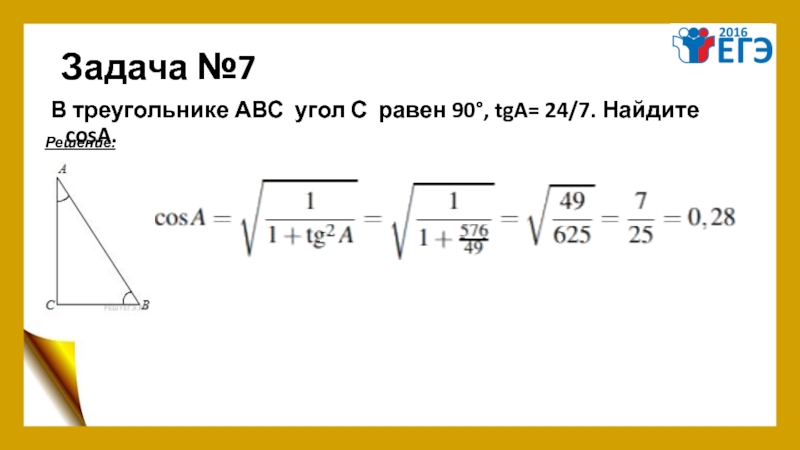
- 11. Задача №7 В треугольнике АВС угол С равен 90°, tgA= 24/7. Найдите cosA. Решение.
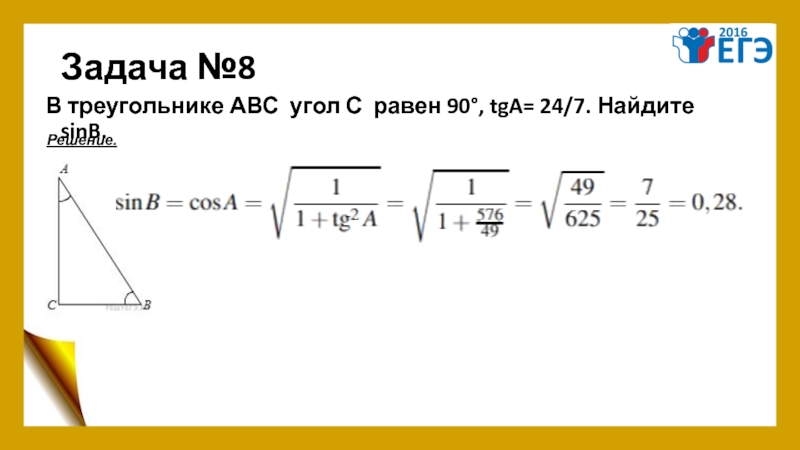
- 12. Задача №8 В треугольнике АВС угол С равен 90°, tgA= 24/7. Найдите sinB. Решение.
- 13. Задача №9 В треугольнике АВС угол С равен 90°, tgA= 2. Найдите tgB. Решение.
- 14. Задача №10 В треугольнике АВС угол С равен 90°, AC=24, BC=7. Найдите sinA. Решение.
- 15. Задача №11 В треугольнике АВС угол С равен 90°, AC=4, AB=8. Найдите cosA. Решение.
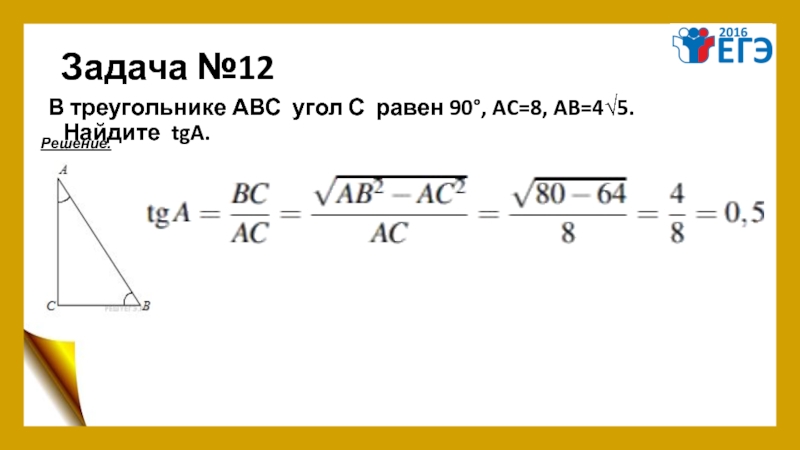
- 16. Задача №12 В треугольнике АВС угол С равен 90°, AC=8, AB=4√5. Найдите tgA. Решение.
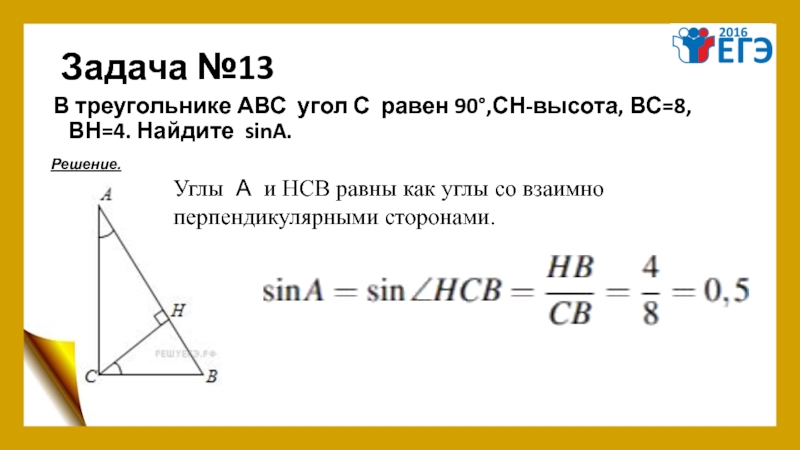
- 17. Задача №13 В треугольнике АВС угол С равен 90°,СН-высота,
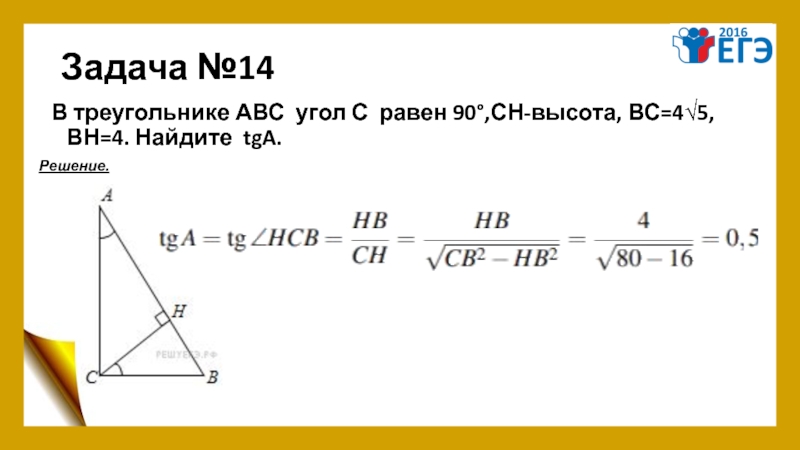
- 18. Задача №14 В треугольнике АВС угол С равен 90°,СН-высота, ВС=4√5, ВН=4. Найдите tgA. Решение.
- 19. Задача №15 В треугольнике АВС угол С равен 90°,СН-высота
- 20. Задача №16 В треугольнике АВС угол С равен 90°,СН-высота
- 21. Задача №17 В треугольнике АВС угол С равен 90.
- 22. Задача №18 В треугольнике АВС угол С равен 90.
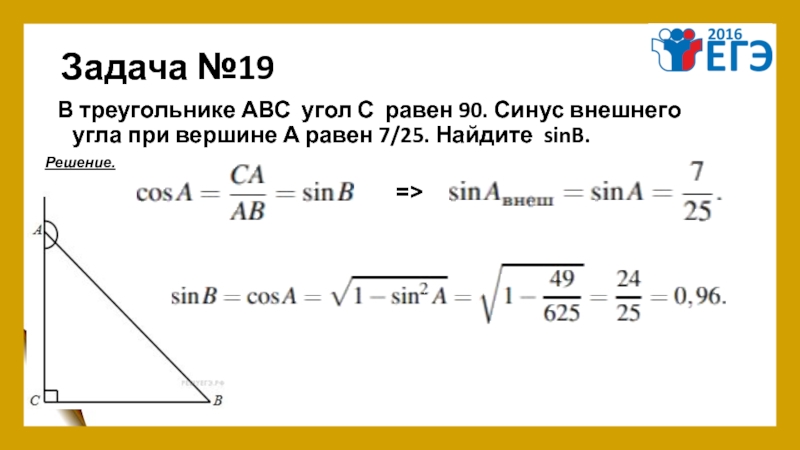
- 23. Задача №19 В треугольнике АВС угол С равен 90.
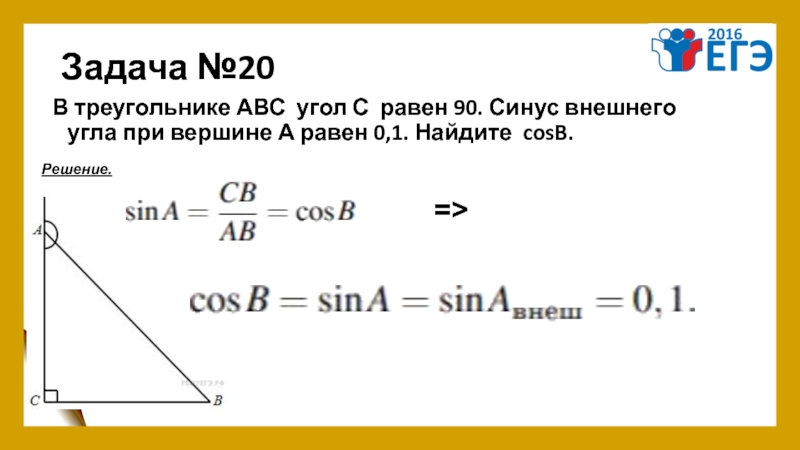
- 24. Задача №20 В треугольнике АВС угол С равен 90.
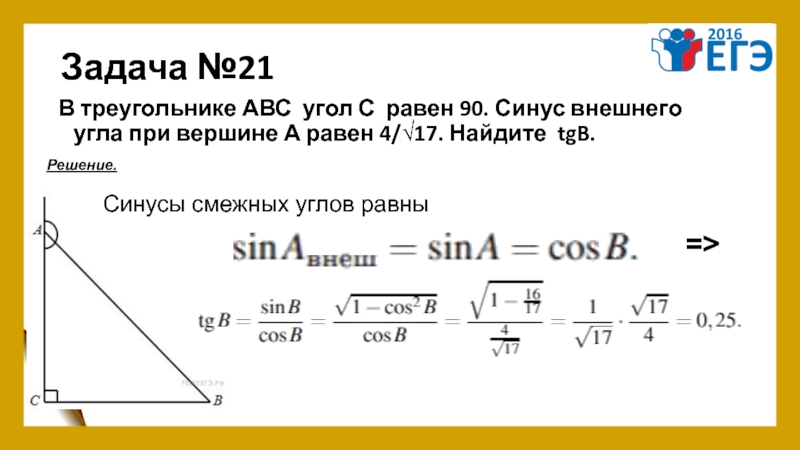
- 25. Задача №21 В треугольнике АВС угол С равен 90.
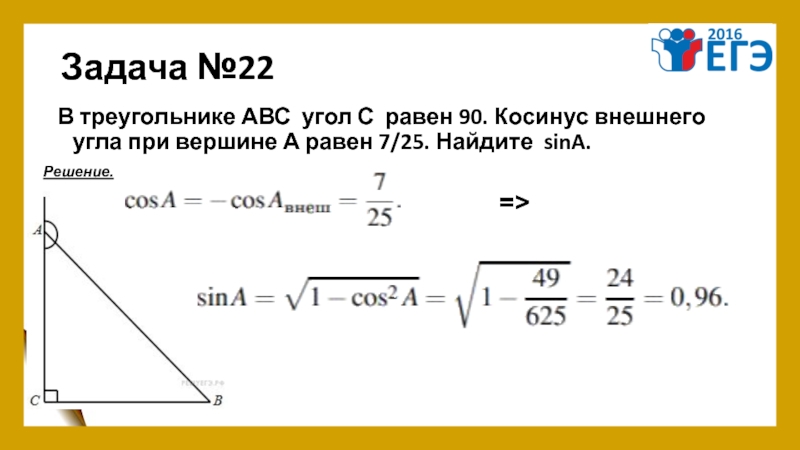
- 26. Задача №22 В треугольнике АВС угол С равен 90.
- 27. Задача №23 Один
- 28. Задача №24 Один острый угол
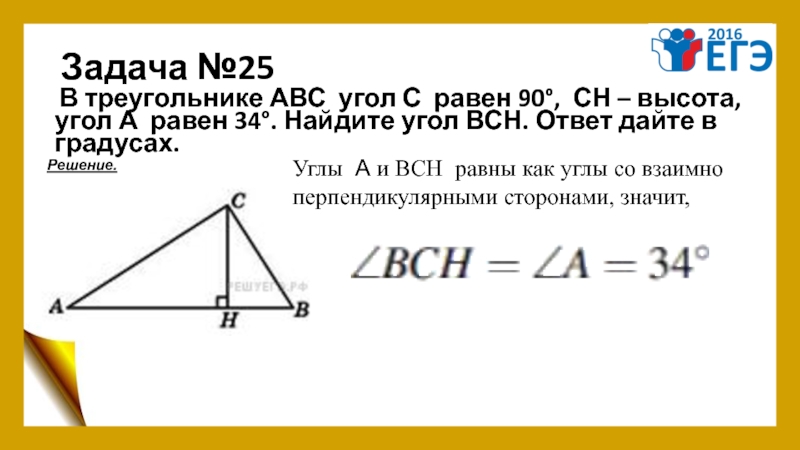
- 29. Задача №25 В треугольнике АВС угол С
- 30. Задача №26 Острые углы прямоугольного треугольника равны
- 31. Задача №27 Острые углы прямоугольного треугольника равны
- 32. Вычисление внешних углов Вычисление внешних углов
- 33. Задача №28 В треугольнике АВС угол С равен 90,
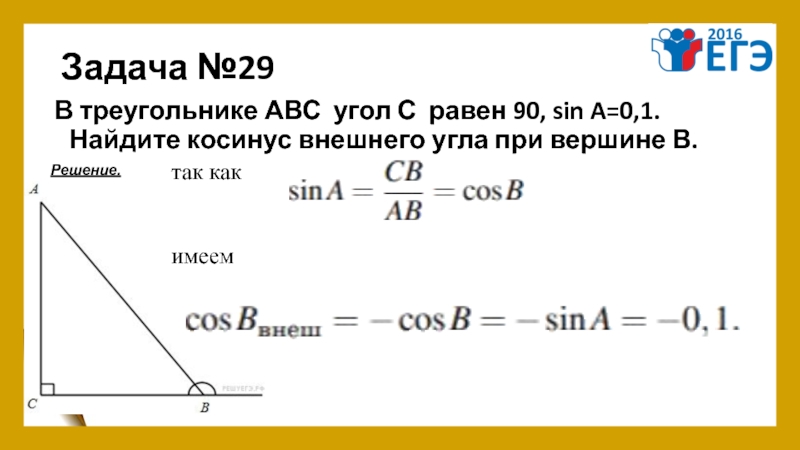
- 34. Задача №29 В треугольнике АВС угол С равен 90,
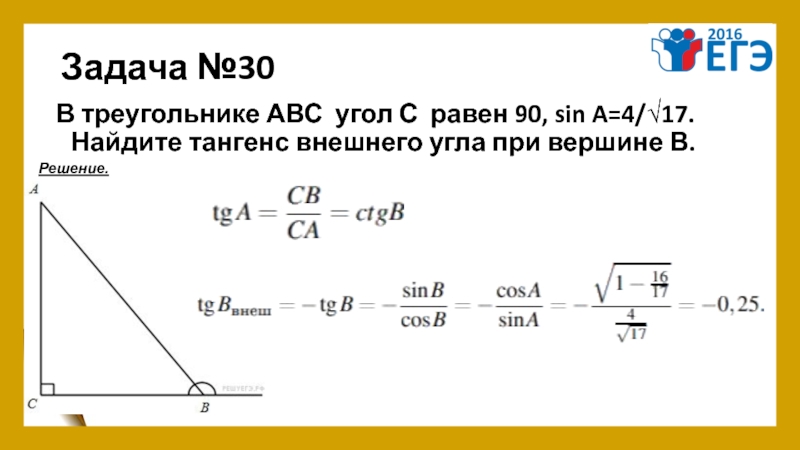
- 35. Задача №30 В треугольнике АВС угол С равен 90,
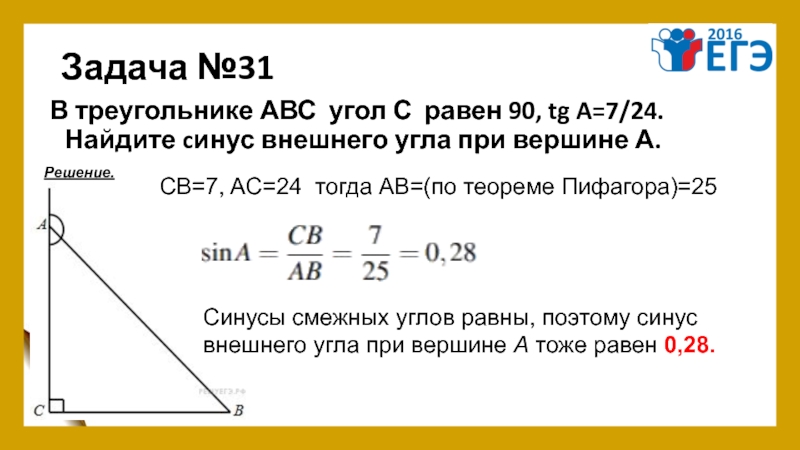
- 36. Задача №31 В треугольнике АВС угол С равен 90,
- 37. Задача №32 В треугольнике АВС угол С равен 90,
- 38. Задача №33 В треугольнике АВС угол С равен 90,
- 39. Задача №34 В треугольнике АВС угол С равен 90,
- 40. Задача №35 треугольнике АВС угол С равен 90, угол
- 41. Задачи для самостоятельного решения
- 42. Решите самостоятельно №1 В треугольнике АВС угол С равен
- 43. Проверим ответы 0,8 2 0,28 0,96 9,5 0,75
- 44. Решите самостоятельно №2 В треугольнике АВС угол С равен
- 45. Проверим ответы … 0,6 0,5 0,28
- 46. Решите самостоятельно №3 В треугольнике АВС угол С равен
- 47. Проверим ответы 0,96 … 0,3 0,1
- 48. Решите самостоятельно №4 Один острый угол прямоугольного
- 49. Проверим ответы … … … 0,5
- 50. Решите самостоятельно №5 В треугольнике АВС угол С
- 51. Решите самостоятельно №6 В треугольнике АВС угол С
- 52. Интернет ресурсы Шаблон подготовлен учителем русского языка
Задания №15 базового уровня с прямоугольным треугольником на вычисление углов
Слайд 1Разработано учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района Республики Коми
Мишариной Альбиной
Геннадьевной
Слайд 3 Содержание
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача №6
Задача №7
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
Задача №19
Задача №20
Задача №21
Задача №22
Задача №23
Задача №24
Задача №25
Задача №26
Задача №27
Задача №28
Задача №29
Задача №30
Задача №31
Задача №32
Задача №33
Задача №34
Задача №35
Задачи для сам. решения
Слайд 4Вспомним
Sin A = cos B
Cos A = sin B
tg A = ctg B
Sin A = Sin внеш. A
Cos A = - Cos внеш. A
tg A = - tg внеш. A
В прямоугольном треугольнике ABC,
с прямым углом С:
Слайд 5Задача №1
В треугольнике АВС угол С равен 90°, sinA= 7/25. Найдите cosA .
Решение.
Ответ:
0,96.
Слайд 8Задача №4
В треугольнике АВС угол С равен 90°, sinA= 0,1. Найдите cosB.
Решение.
cosB =
sinA= 0,1.
Слайд 17Задача №13
В треугольнике АВС угол С равен 90°,СН-высота, ВС=8, ВН=4. Найдите sinA.
Решение.
Углы А и НСВ равны
как углы со взаимно
перпендикулярными сторонами.
перпендикулярными сторонами.
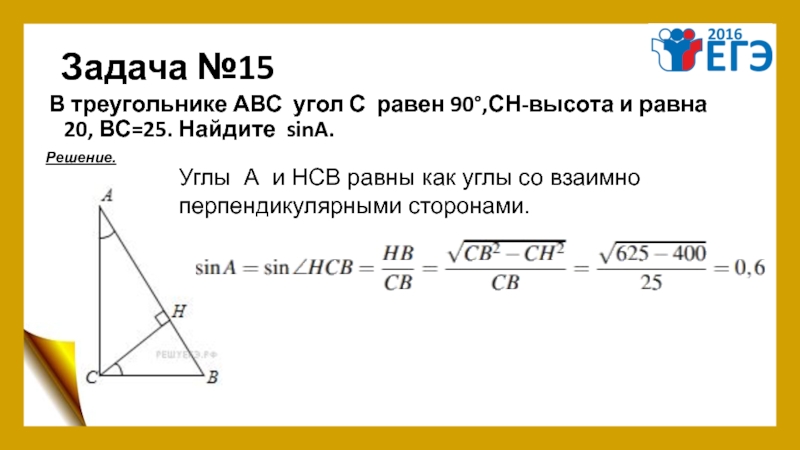
Слайд 19Задача №15
В треугольнике АВС угол С равен 90°,СН-высота и равна 20, ВС=25. Найдите
sinA.
Решение.
Углы А и НСВ равны как углы со взаимно
перпендикулярными сторонами.
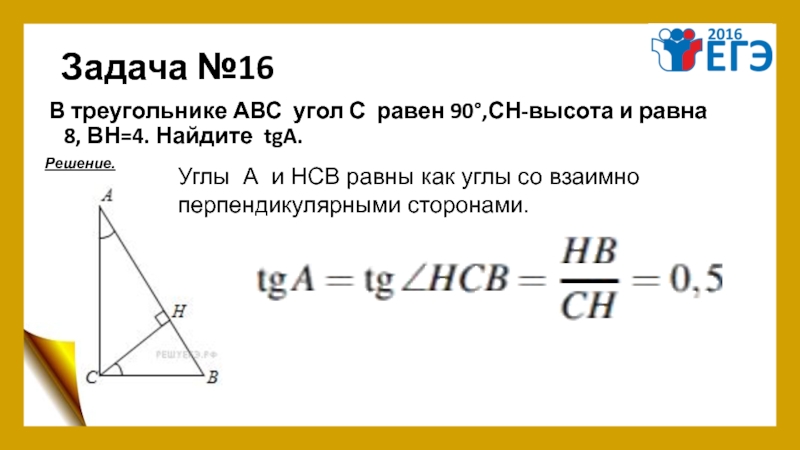
Слайд 20Задача №16
В треугольнике АВС угол С равен 90°,СН-высота и равна 8, ВН=4. Найдите
tgA.
Решение.
Углы А и НСВ равны как углы со взаимно
перпендикулярными сторонами.
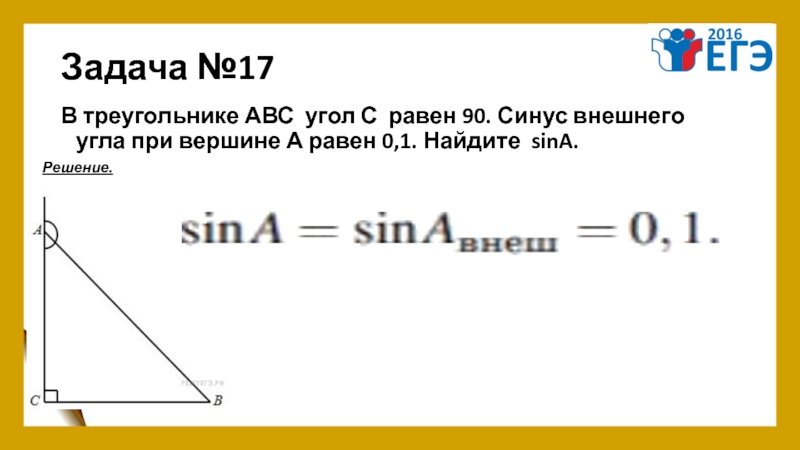
Слайд 21Задача №17
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
А равен 0,1. Найдите sinA.
Решение.
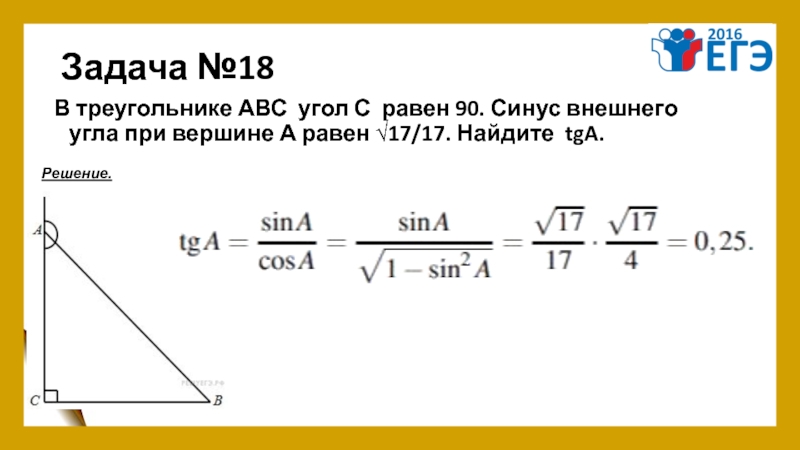
Слайд 22Задача №18
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
А равен √17/17. Найдите tgA.
Решение.
Слайд 23Задача №19
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
А равен 7/25. Найдите sinB.
Решение.
=>
Слайд 24Задача №20
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
А равен 0,1. Найдите cosB.
Решение.
=>
Слайд 25Задача №21
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
А равен 4/√17. Найдите tgB.
Решение.
Синусы смежных углов равны
=>
Слайд 26Задача №22
В треугольнике АВС угол С равен 90. Косинус внешнего угла при вершине
А равен 7/25. Найдите sinA.
Решение.
=>
Слайд 27Задача №23
Один острый угол прямоугольного треугольника на
32° больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Решение.
Сумма острых углов прямоугольного треугольника равна 90°, значит, если меньший из них обозначить за Х, то другой будет (Х+32°).
Тогда: Х+(Х+32°) = 90° => 2Х=90°- 32°
2Х =58°, т.е. Х=29°. Значит больший угол равен 29°+32°= 61°
Слайд 28Задача №24
Один острый угол прямоугольного треугольника в 4 раза больше
другого. Найдите больший острый угол. Ответ дайте в градусах.
Решение.
Обозначим меньший острый угол прямоугольного
треугольника за х, тогда больший острый угол
будет равен 4х . Имеем
Значит, больший острый угол равен
Слайд 29Задача №25
В треугольнике АВС угол С равен 90°, СН – высота, угол А равен
34°. Найдите угол ВСН. Ответ дайте в градусах.
Решение.
Углы А и ВСН равны как углы со взаимно
перпендикулярными сторонами, значит,
Слайд 30Задача №26
Острые углы прямоугольного треугольника равны 85° и 5°. Найдите угол
между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение.
Углы САН и ВАС равны, как углы сo
взаимно перпендикулярными сторонами.
Из прямоугольного треугольника DCH:
Слайд 31Задача №27
Острые углы прямоугольного треугольника равны 62° и 28°. Найдите угол
между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Решение.
Медиана, проведённая к гипотенузе, равна её
половине, поэтому треугольник ACF –
равнобедренный. Тогда угол АСF=28°.
Поскольку CH — высота, то угол ВСН=90°-62°=28°.
Поэтому для искомого угла имеем:
Слайд 33Задача №28
В треугольнике АВС угол С равен 90, sin A=0,1. Найдите cинус внешнего
угла при вершине А.
Решение.
Синусы смежных углов равны, значит, синус
внешнего угла при вершине А равен синусу угла А
и равен 0,1.
Слайд 34Задача №29
В треугольнике АВС угол С равен 90, sin A=0,1. Найдите косинус внешнего
угла при вершине В.
Решение.
так как
имеем
Слайд 35Задача №30
В треугольнике АВС угол С равен 90, sin A=4/√17. Найдите тангенс внешнего
угла при вершине В.
Решение.
Слайд 36Задача №31
В треугольнике АВС угол С равен 90, tg A=7/24. Найдите cинус внешнего
угла при вершине А.
Решение.
CB=7, AC=24 тогда АВ=(по теореме Пифагора)=25
Синусы смежных углов равны, поэтому синус
внешнего угла при вершине А тоже равен 0,28.
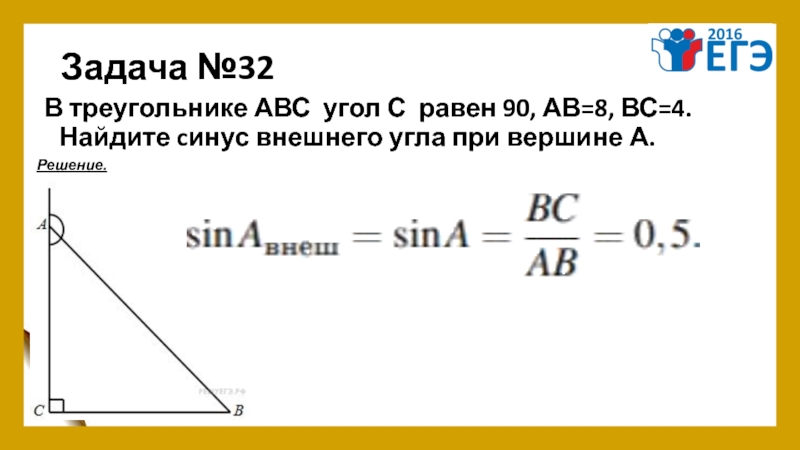
Слайд 37Задача №32
В треугольнике АВС угол С равен 90, АВ=8, ВС=4. Найдите cинус внешнего
угла при вершине А.
Решение.
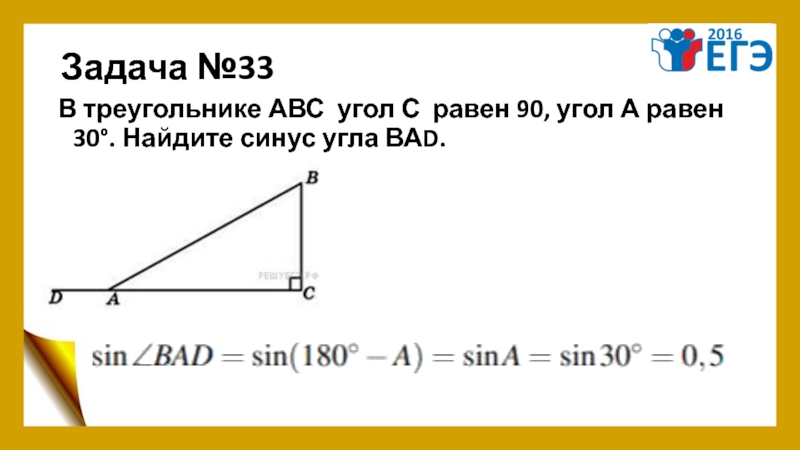
Слайд 38Задача №33
В треугольнике АВС угол С равен 90, угол А равен 30°. Найдите
синус угла ВАD.
Решение.
Слайд 39Задача №34
В треугольнике АВС угол С равен 90, угол А равен 30°. Найдите
koсинус угла ВАD. В ответе укажите √3·cosBAD.
Решение.
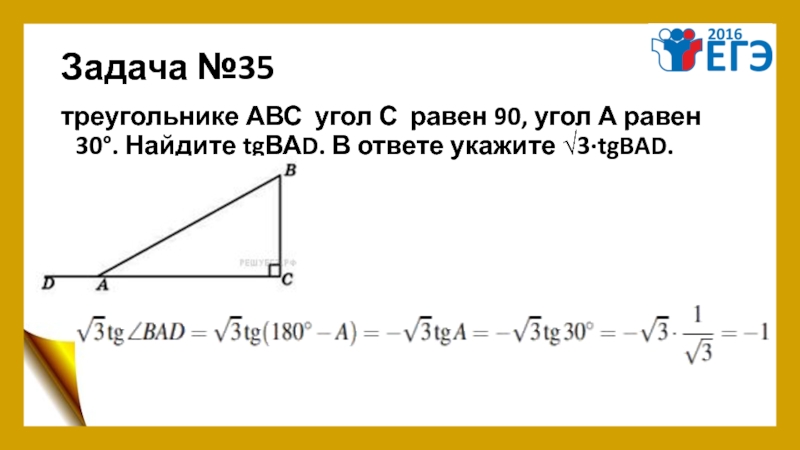
Слайд 40Задача №35
треугольнике АВС угол С равен 90, угол А равен 30°. Найдите tgВАD.
В ответе укажите √3·tgBAD.
Решение.
Слайд 42Решите самостоятельно №1
В треугольнике АВС угол С равен 90°, sinA= 3/5. Найдите cosA.
В треугольнике АВС
угол С равен 90°, sinA= 2√5/5. Найдите tgA.
В треугольнике АВС угол С равен 90°, sinA= 24/25. Найдите sinB.
В треугольнике АВС угол С равен 90°, tgA= 7/24. Найдите sinB.
В треугольнике АВС угол С равен 90°, tgA= 2/19. Найдите tgB.
В треугольнике АВС угол С равен 90°, AC=8, AB=10. Найдите tgA.
В треугольнике АВС угол С равен 90°, sinA= 24/25. Найдите sinB.
В треугольнике АВС угол С равен 90°, tgA= 7/24. Найдите sinB.
В треугольнике АВС угол С равен 90°, tgA= 2/19. Найдите tgB.
В треугольнике АВС угол С равен 90°, AC=8, AB=10. Найдите tgA.
Слайд 44Решите самостоятельно №2
В треугольнике АВС угол С равен 90°,СН-высота, ВС=20, ВН=16. Найдите sinA.
В
треугольнике АВС угол С равен 90°,СН-высота, ВС=25, ВН=20. Найдите cosA.
В треугольнике АВС угол С равен 90°,СН-высота и равна 4, ВС=8. Найдите cosA.
В треугольнике АВС угол С равен 90°,СН-высота и равна 7, ВН=24. Найдите cosA.
В треугольнике АВС угол С равен 90°,СН-высота и равна 4, ВС=8. Найдите cosA.
В треугольнике АВС угол С равен 90°,СН-высота и равна 7, ВН=24. Найдите cosA.
Слайд 46Решите самостоятельно №3
В треугольнике АВС угол С равен 90. Синус внешнего угла при
вершине А равен 7/25. Найдите cosA.
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине А равен 0,51. Найдите cosB.
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине А равен 10/√109. Найдите tgB.
4) В треугольнике АВС угол С равен 90. Косинус внешнего угла при вершине А равен – 0,1. Найдите cosA.
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине А равен 0,51. Найдите cosB.
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине А равен 10/√109. Найдите tgB.
4) В треугольнике АВС угол С равен 90. Косинус внешнего угла при вершине А равен – 0,1. Найдите cosA.
Слайд 48Решите самостоятельно №4
Один острый угол прямоугольного треугольника на 6° больше другого. Найдите
больший острый угол. Ответ дайте в градусах.
Один острый угол прямоугольного треугольника в 19\11 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.
В треугольнике АВС угол С равен 90°, СН – высота, угол А равен 49°. Найдите угол ВСН. Ответ дайте в градусах.
В треугольнике ABC угол С равен 90°, АВ = 4, ВС = 2. Найдите sin A .
Один острый угол прямоугольного треугольника в 19\11 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.
В треугольнике АВС угол С равен 90°, СН – высота, угол А равен 49°. Найдите угол ВСН. Ответ дайте в градусах.
В треугольнике ABC угол С равен 90°, АВ = 4, ВС = 2. Найдите sin A .
Слайд 50Решите самостоятельно №5
В треугольнике АВС угол С равен 90, sin A=0,51. Найдите
cинус внешнего угла при вершине А.
В треугольнике АВС угол С равен 90, sin A=7/25. Найдите коcинус внешнего угла при вершине А.
Ответ: -0,96
3) В треугольнике АВС угол С равен 90, sin A=√17/17. Найдите тангенс внешнего угла при вершине А.
Ответ: - 0,25
В треугольнике АВС угол С равен 90, sin A=7/25. Найдите коcинус внешнего угла при вершине А.
Ответ: -0,96
3) В треугольнике АВС угол С равен 90, sin A=√17/17. Найдите тангенс внешнего угла при вершине А.
Ответ: - 0,25
Слайд 51Решите самостоятельно №6
В треугольнике АВС угол С равен 90, sin A=7/25. Найдите
синус внешнего угла при вершине В. Ответ: 0,96
В треугольнике АВС угол С равен 90, cos A=7/25. Найдите синус внешнего угла при вершине A. Ответ: 0,96
В треугольнике АВС угол С равен 90, cos A=0,1. Найдите koсинус внешнего угла при вершине A. Ответ:-0,1
4) В треугольнике АВС угол С равен 90, tg A=4/3. Найдите cинус внешнего угла при вершине А.
В треугольнике АВС угол С равен 90, cos A=7/25. Найдите синус внешнего угла при вершине A. Ответ: 0,96
В треугольнике АВС угол С равен 90, cos A=0,1. Найдите koсинус внешнего угла при вершине A. Ответ:-0,1
4) В треугольнике АВС угол С равен 90, tg A=4/3. Найдите cинус внешнего угла при вершине А.
Слайд 52Интернет ресурсы
Шаблон подготовлен учителем русского языка и литературы Тихоновой Надеждой Андреевной
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
«Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа: http://mathb.reshuege.ru
