- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Развертки поверхностей. (Занятие 13) презентация
Содержание
- 1. Развертки поверхностей. (Занятие 13)
- 2. 1. Развертки поверхностей Разверткой поверхности называется плоская
- 3. Развертки могут быть точные, приближенные и условные.
- 4. Свойства разверток: 1. Длины соответствующих линий
- 5. Развертка многогранников Разверткой многогранника является плоская фигура,
- 6. Упражнение: Построить развертку прямой усеченной четырехгранной
- 7. Развертка прямой трехгранной пирамиды Развертка боковой поверхности
- 8. Упражнение: Построить развертку боковой поверхности наклонной
- 9. Развертка тел вращения Развертка прямого кругового цилиндра
- 10. Построение развертки прямого кругового усеченного цилиндра
- 11. Развертка прямого кругового конуса Развертка поверхности
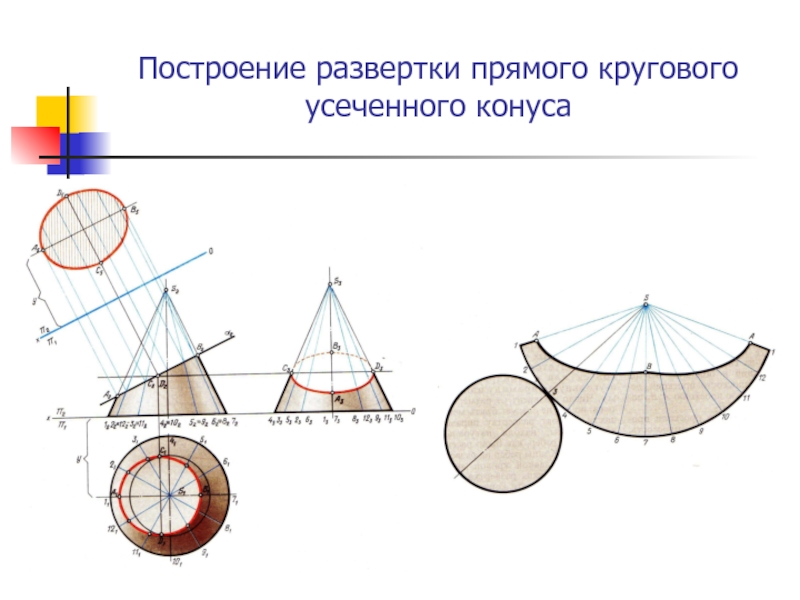
- 12. Построение развертки прямого кругового усеченного конуса
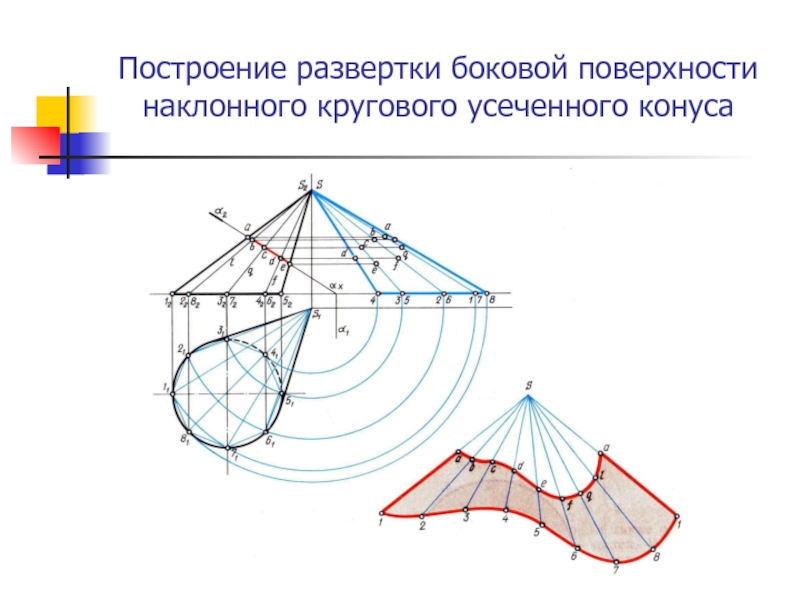
- 13. Построение развертки боковой поверхности наклонного кругового усеченного конуса
- 14. Развертка неразвертываемых поверхностей (сфера, тор и т.п)
Слайд 21. Развертки поверхностей
Разверткой поверхности называется плоская геометрическая фигура, полученная в результате
Развертка поверхностей является основой для построения выкроек изделий из листового материала, которым затем путем свертывания и соединения при помощи сварки, пайки или других сборочных операций придается требуемая форма изделия.
С помощью разверток (точных или приближенных) рассчитывается площадь поверхности изделий (зданий, сооружений), покрываемых различными материалами, например окрашиваемых поверхностей.
Поверхности делятся на развертываемые - поверхности многогранников, цилиндров, конусов и неразвертываемые -сферические, торовые.
Слайд 3Развертки могут быть точные, приближенные и условные.
Точные развертки при обратном
Точные развертки строят для поверхностей многогранников (призмы, пирамиды), приближенные развертки строят для остальных развертываемых поверхностей.
Для неразвертываемых поверхностей строят условные развертки.
Слайд 4Свойства разверток:
1. Длины соответствующих линий (ребер, образующих и т.п.) на
2. Площадь поверхности, ограниченная определенными линиями, равна площади развертки, ограниченной теми же линиями;
3. Углы между соответствующими линиями на поверхности и развертке равны;
4. Прямым линиям на поверхности соответствуют прямые линии на развертке;
5. Кратчайшей линии между двумя точками на поверхности соответствует прямая линия на развертке.
Слайд 5Развертка многогранников
Разверткой многогранника является плоская фигура, полученная при совмещении всех его
Все грани многоугольника на развертке представляются в натуральную величину, то есть построение развертки сводится к построению натуральных величин граней многогранника.
Развертка прямой трехгранной призмы:
Длина развертки боковой поверхности призмы равна сумме длин сторон треугольника основания,
Высота боковой поверхности равна высоте призмы.
К развертке боковой поверхности пристраиваются два основания призмы.
Слайд 6
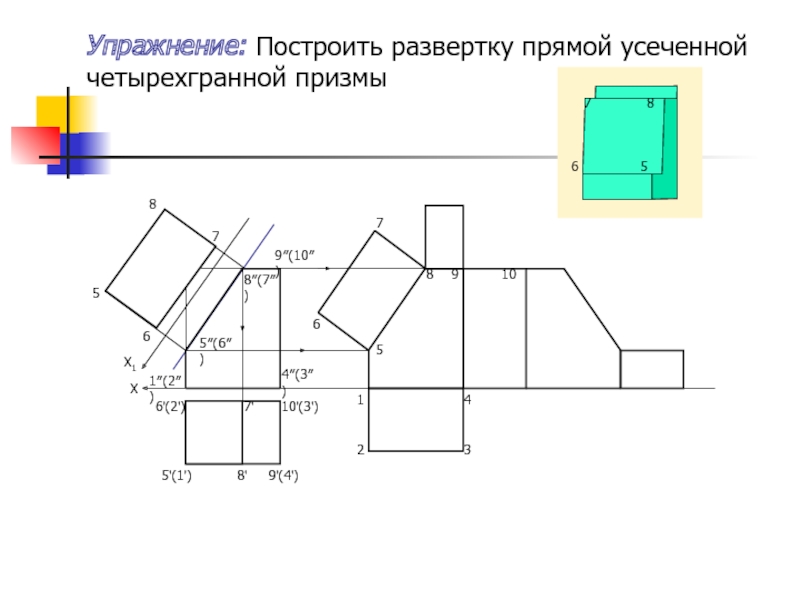
Упражнение: Построить развертку прямой усеченной четырехгранной призмы
1″(2″)
4″(3″)
5″(6″)
8″(7″)
9″(10″)
5'(1')
6'(2')
8'
7'
9'(4')
10'(3')
6
5
8
7
1
2
3
4
5
6
8
7
5
6
7
8
9
10
Х
Х1
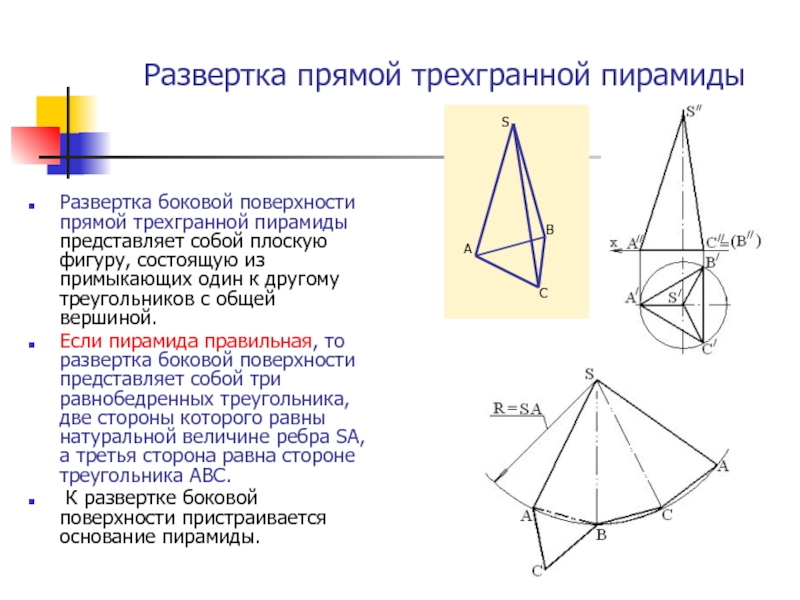
Слайд 7Развертка прямой трехгранной пирамиды
Развертка боковой поверхности прямой трехгранной пирамиды представляет собой
Если пирамида правильная, то развертка боковой поверхности представляет собой три равнобедренных треугольника, две стороны которого равны натуральной величине ребра SA, а третья сторона равна стороне треугольника АВС.
К развертке боковой поверхности пристраивается основание пирамиды.
Слайд 8
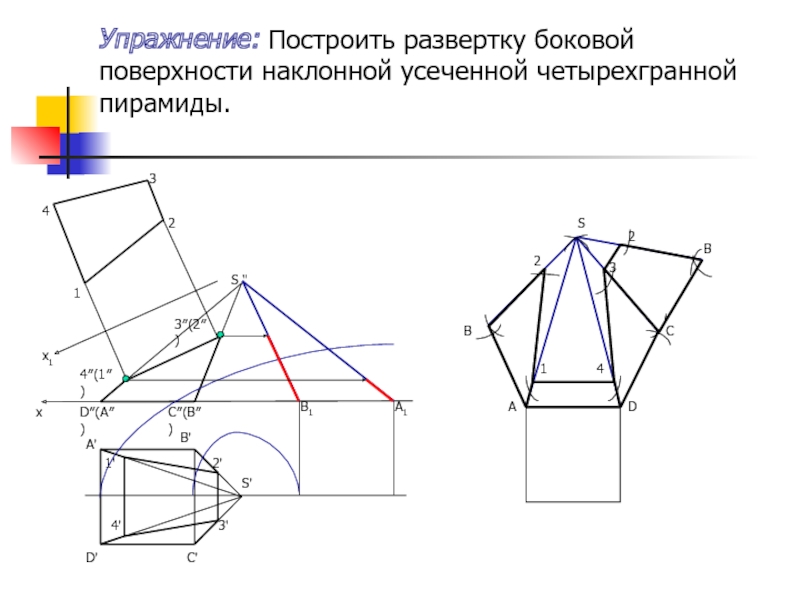
Упражнение: Построить развертку боковой поверхности наклонной усеченной четырехгранной пирамиды.
S'
S ''
x
x1
A'
B'
C'
D'
D″(A″)
C″(B″)
4″(1″)
3″(2″)
1'
2'
3'
4'
1
4
2
3
A
D
S
1
4
B
2
C
3
B
2
B1
A1
Слайд 9Развертка тел вращения
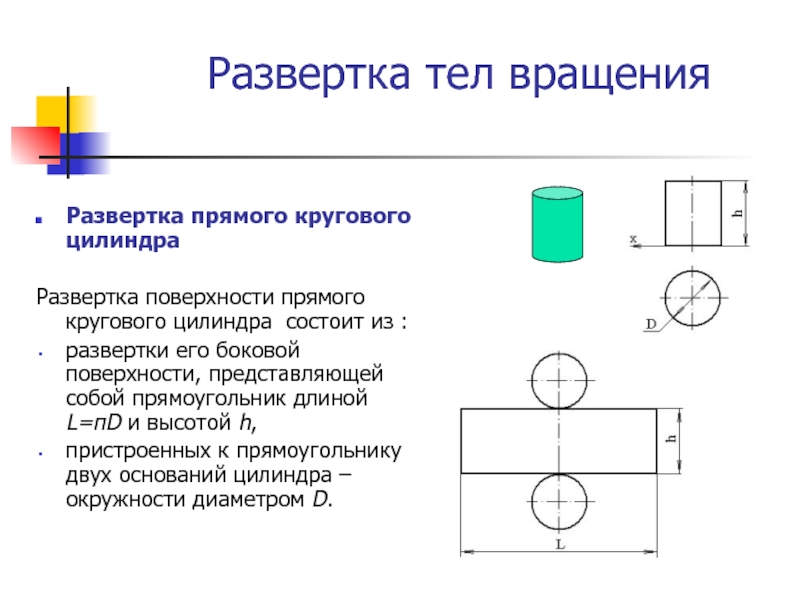
Развертка прямого кругового цилиндра
Развертка поверхности прямого кругового цилиндра состоит
развертки его боковой поверхности, представляющей собой прямоугольник длиной L=πD и высотой h,
пристроенных к прямоугольнику двух оснований цилиндра – окружности диаметром D.
Слайд 11
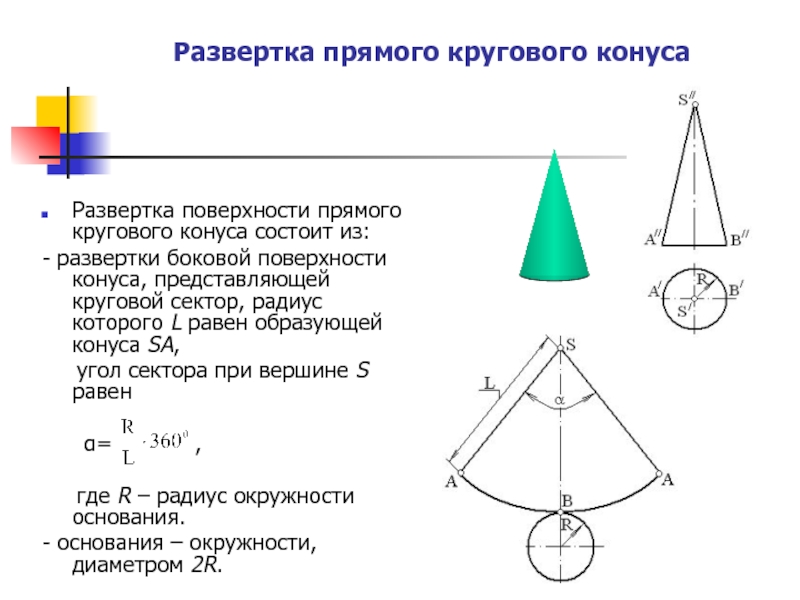
Развертка прямого кругового конуса
Развертка поверхности прямого кругового конуса состоит из:
- развертки
угол сектора при вершине S равен
α= ,
где R – радиус окружности основания.
- основания – окружности, диаметром 2R.
Слайд 14Развертка неразвертываемых поверхностей (сфера, тор и т.п)
Развертка поверхности сферы.
Сначала сфера
Поверхность каждого сферического отсека аппроксимируется цилиндрической поверхностью, направляющей которой является полуокружность, а образующие перпендикулярны фронтальной плоскости проекций.
На рисунке показана условная развертка сферы, состоящая из 8 частей - равных разверток конических отсеков, аппроксимирующих сферу.
Для построения разверток неразвертываемых поверхностей отдельные участки этих поверхностей (отсеки) условно заменяют приближенными участками развертываемых поверхностей. То есть, неразвертываемая поверхность аппроксимируется совокупностью отсеков поверхностей с известной формой развертки.