- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множественная регрессия презентация
Содержание
- 1. Множественная регрессия
- 2. Множественная регрессия – это уравнение статистической связи
- 3. Факторы, включаемые во множественную регрессию, должны отвечать
- 4. Считается, что две переменные явно коллинеарны, т.е.
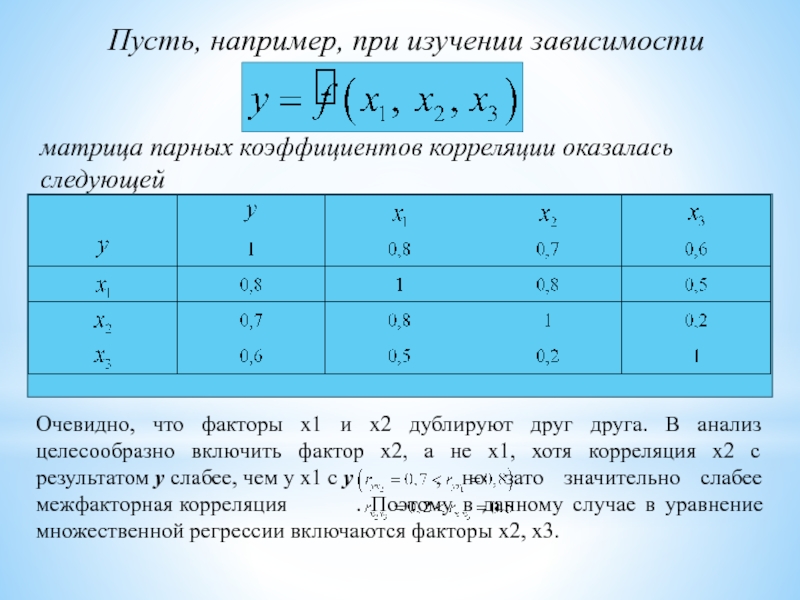
- 5. Пусть, например, при изучении зависимости
- 6. Включение в модель мультиколлинеарных факторов нежелательно в
- 7. Если бы факторы не коррелировали между собой,
- 8. Одним из путей учета внутренней корреляции
- 9. Наиболее широкое применение получили следующие методы построения
- 10. Метод наименьших квадратов (МНК). Свойства оценок на
- 11. Имеем функцию аргумента: Находим частные производные первого порядка:
- 12. После элементарных преобразований приходим к системе линейных
- 13. МНК применим и к уравнению множественной регрессии
- 14. Применяя МНК к уравнению множественной регрессии в
- 15. Коэффициенты «чистой» регрессии связаны со стандартизованными
- 16. При подстановке в эти уравнения средних значений
- 17. На основе частных уравнений регрессии определяются частные
Слайд 1Тема 4. Множественная регрессия.
Модель с двумя независимыми переменными.
Оценка коэффициентов модели
Парная и частная корреляция в модели множественной регрессии.
Оценка качества модели множественной регрессии.
Мультиколлинеарность и методы ее устранения.
Интерпретация коэффициентов модели множественной регрессии.
Слайд 2Множественная регрессия – это уравнение статистической связи с несколькими независимыми переменными:
y
где y – зависимая переменная (результативный признак);
x1, x2, …, xp – независимые переменные (факторы).
Слайд 3Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
Они должны быть
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Слайд 4 Считается, что две переменные явно коллинеарны, т.е. находятся между собой в
Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.
Слайд 5Пусть, например, при изучении зависимости
матрица парных коэффициентов корреляции оказалась следующей
Очевидно,
Слайд 6Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
1) Затрудняется
2) Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
Слайд 7 Если бы факторы не коррелировали между собой, то матрица парных коэффициентов
были бы равны нулю.
Так, для уравнения, включающего три объясняющих переменных
матрица коэффициентов корреляции между факторами имела бы определитель, равный единице:
Слайд 8
Одним из путей учета внутренней корреляции факторов является переход к совмещенным
то возможно построение следующего совмещенного уравнения:
Слайд 9Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
Метод исключения
2) Метод включения – дополнительное введение фактора.
3) Шаговый регрессионный анализ – исключение ранее введенного фактора.
Слайд 10Метод наименьших квадратов (МНК).
Свойства оценок на основе МНК
В линейной множественной регрессии
параметры при Х называются коэффициентами «чистой» регрессии.
Рассмотрим линейную модель множественной регрессии
(1)
МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных минимальна:
(2)
Слайд 12 После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения
(3)
Для двухфакторной модели данная система будет иметь вид:
Слайд 13МНК применим и к уравнению множественной регрессии в стандартизированном масштабе:
(4)
где
– стандартизированные
для которых среднее значение равно нулю:
а среднее квадратическое отклонение равно единице:
– стандартизированные коэффициенты регрессии.
Слайд 14 Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему
(5)
Где и – коэффициенты парной и межфакторной корреляции
Слайд 15 Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами регрессии
(6)
Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (4) к уравнению регрессии в натуральном масштабе переменных (1), при этом параметр а определяется как
На основе линейного уравнения множественной регрессии
(7)
могут быть найдены частные уравнения регрессии:
(8)
Слайд 16 При подстановке в эти уравнения средних значений соответствующих факторов они принимают
(9)
где
Слайд 17На основе частных уравнений регрессии определяются частные коэффициенты эластичности:
(10)
Где
– частное уравнение регрессии.
Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:
(11)