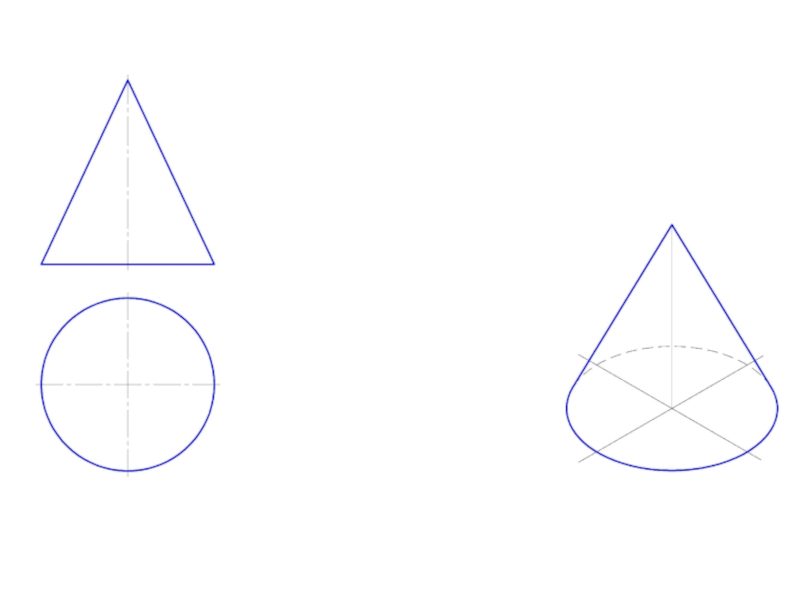
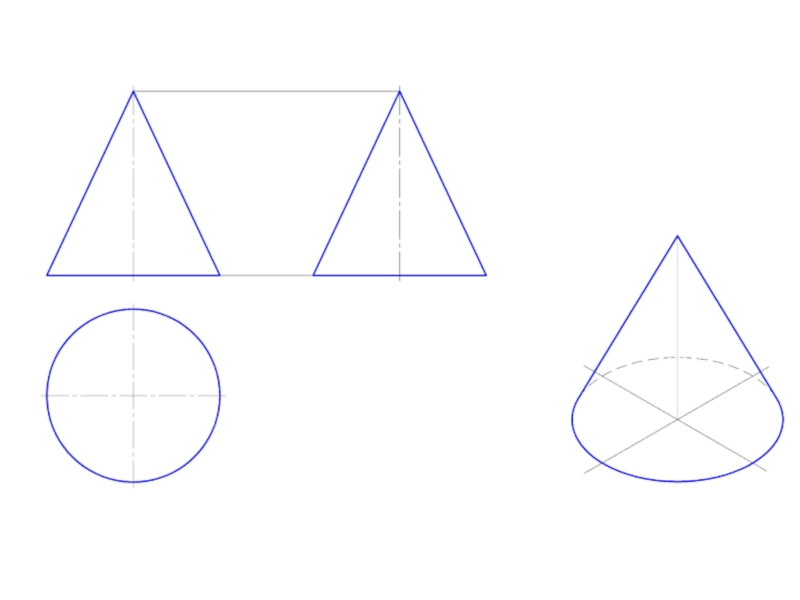
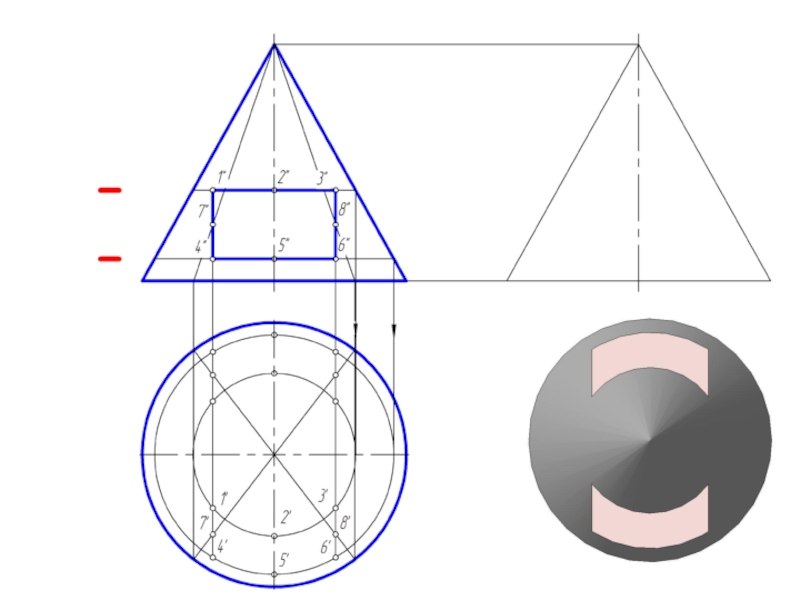
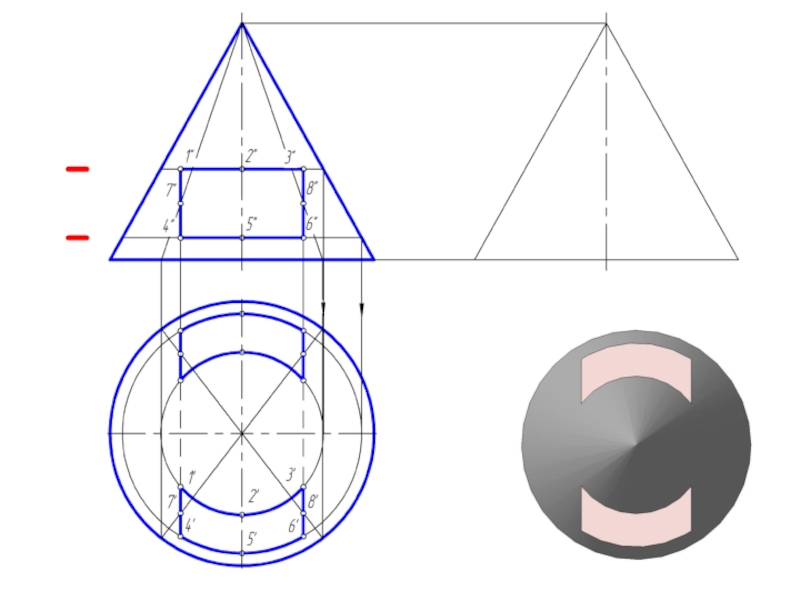
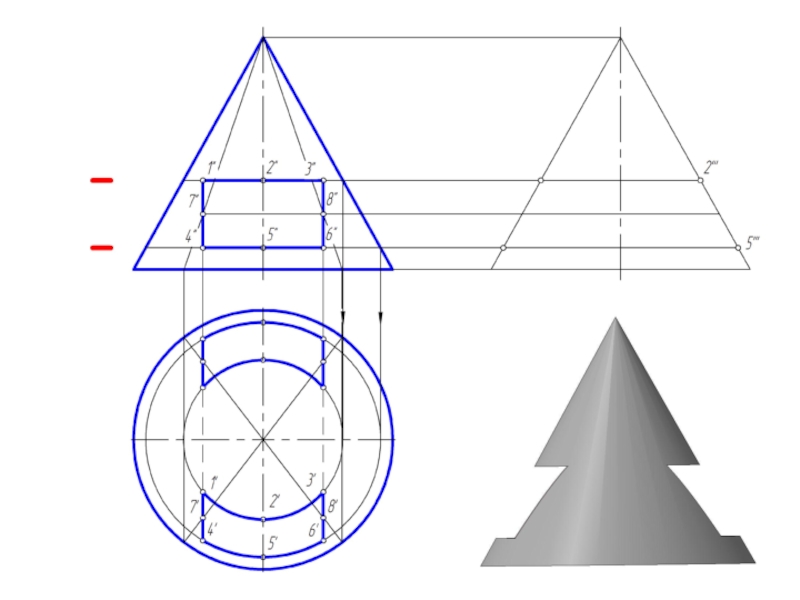
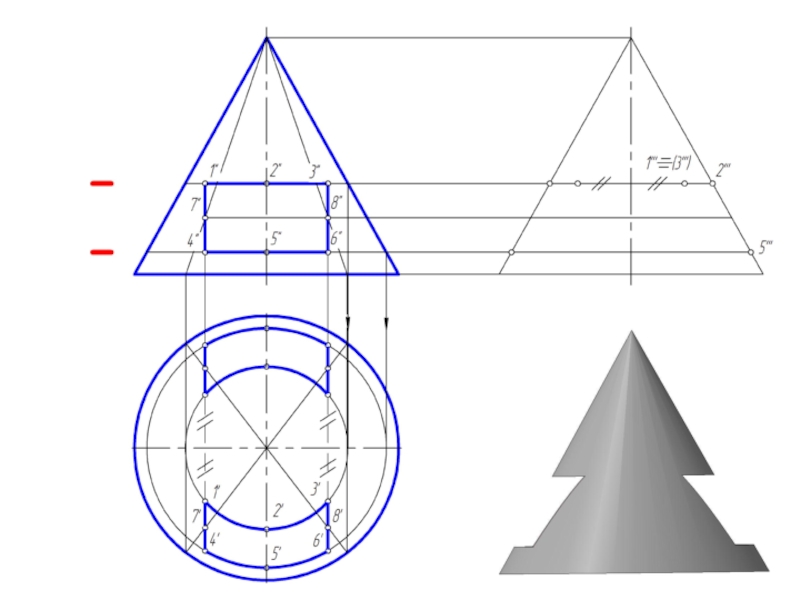
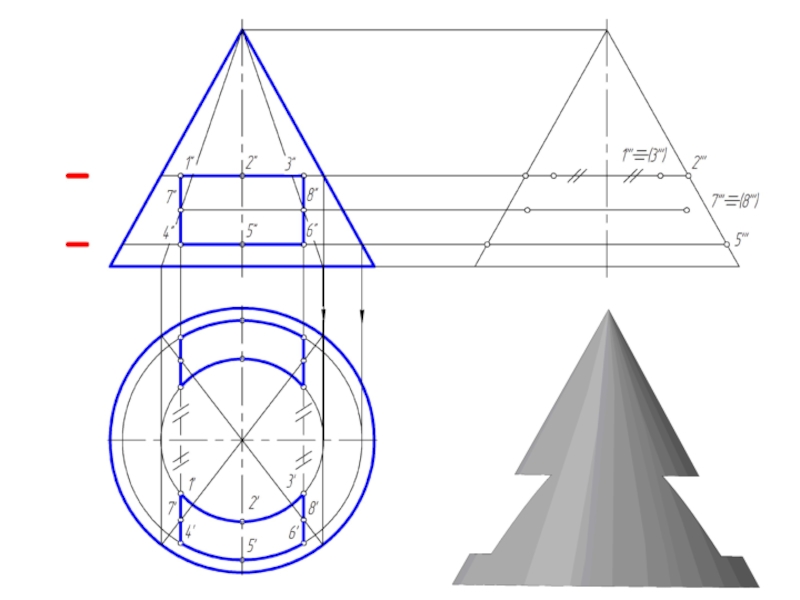
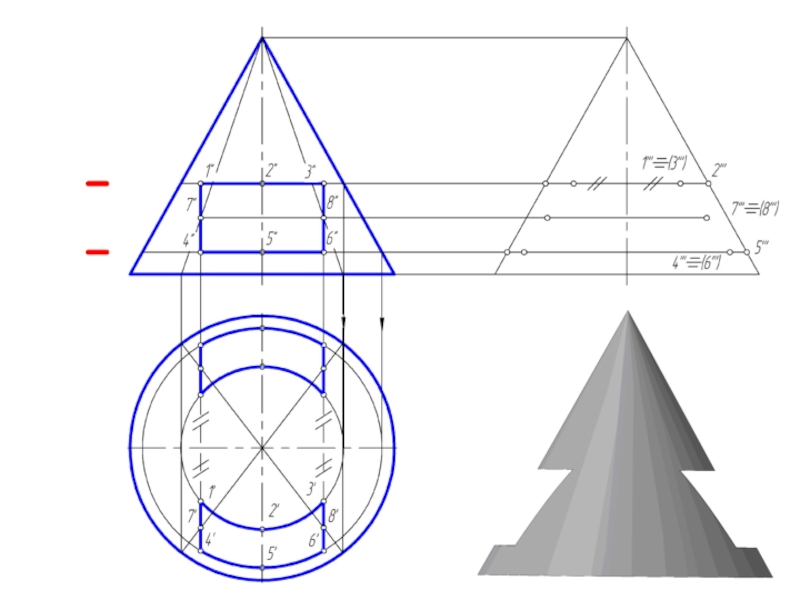
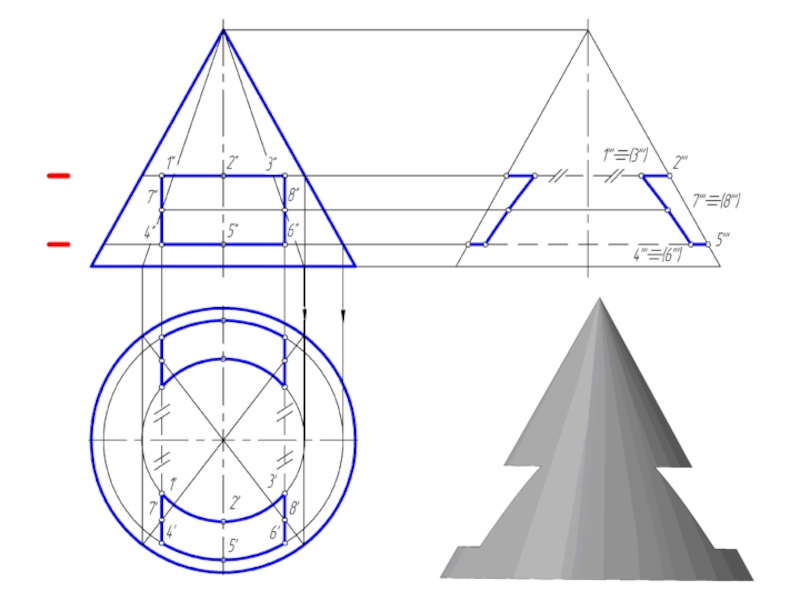
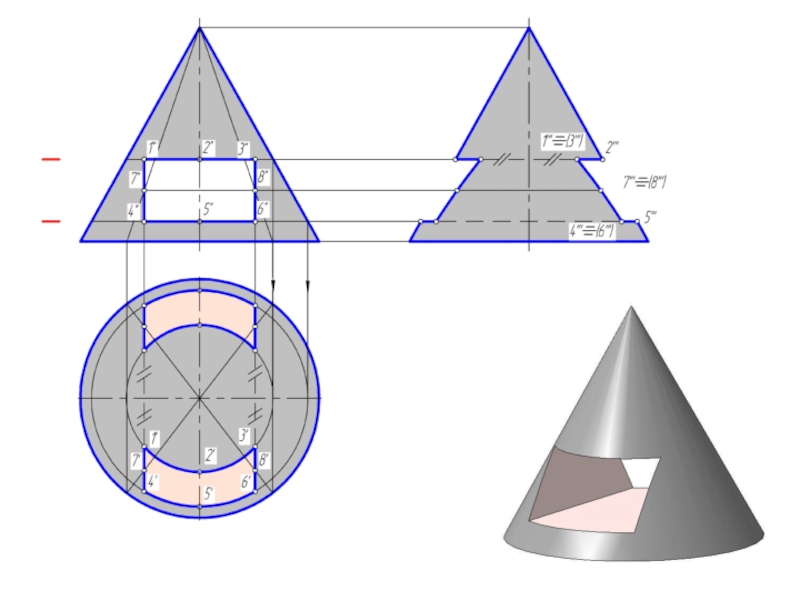
и плоскостью, перпендикулярной к ее оси. Меридианы такого конуса – треугольники.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямой круговой конус презентация
Содержание
- 1. Прямой круговой конус
- 2. Точка на поверхности прямого кругового конуса Точку,
- 11. Пересечение прямого кругового конуса плоскостью Треугольник (две
- 12. Если конус пересекается плоскостью, не проходящей
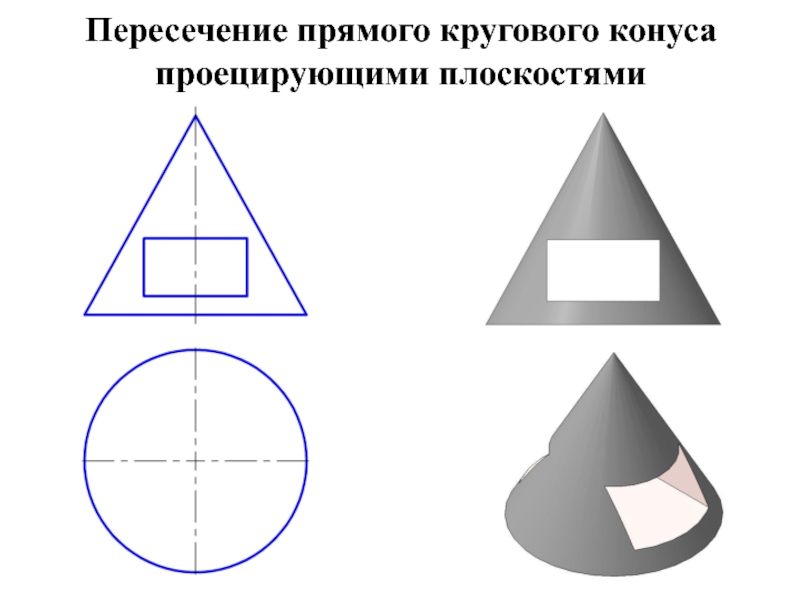
- 14. Пересечение прямого кругового конуса проецирующими плоскостями
- 27. Пересечение прямого кругового конуса прямой линией При
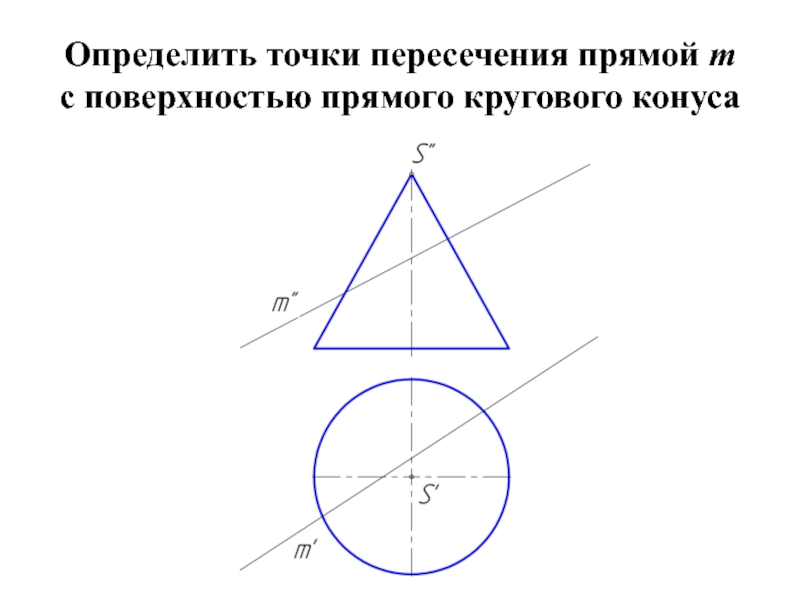
- 28. Определить точки пересечения прямой m с поверхностью прямого кругового конуса
- 29. 1. Заключаем прямую m в плоскость
- 30. Определяем линию, по которой построенная плоскость
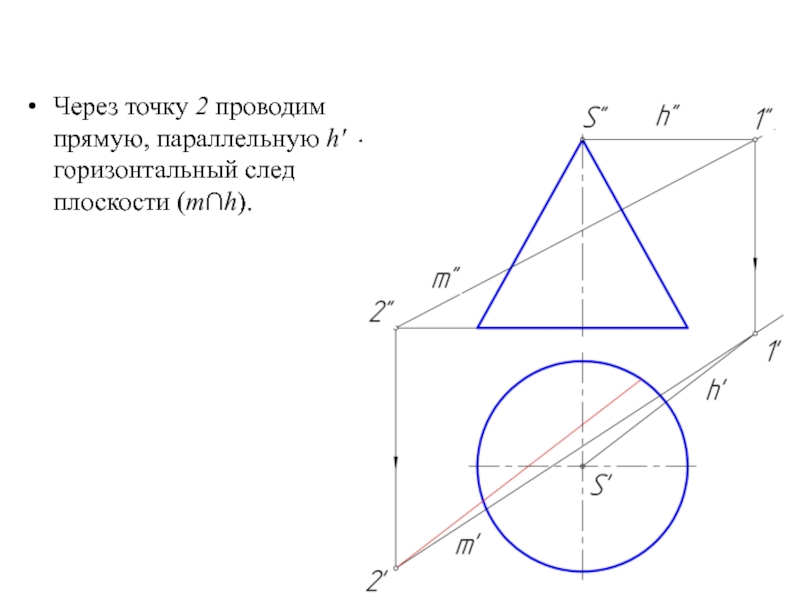
- 31. Через точку 2 проводим прямую, параллельную h' - горизонтальный след плоскости (m∩h).
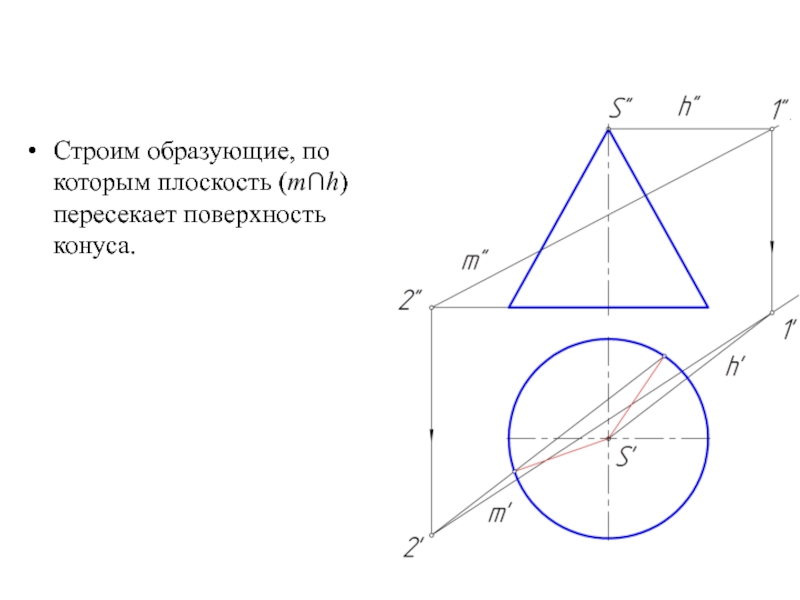
- 32. Строим образующие, по которым плоскость (m∩h) пересекает поверхность конуса.
- 33. Отмечаем точки, в которых образующие пересекают
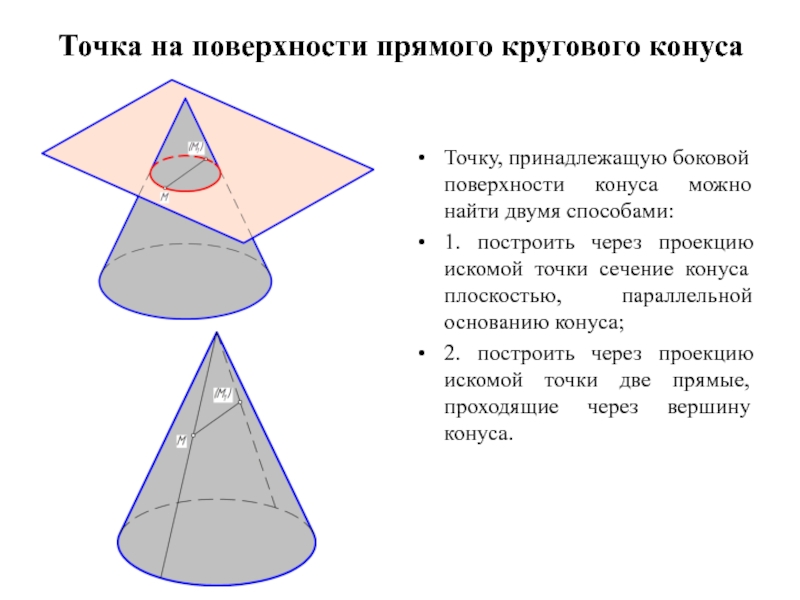
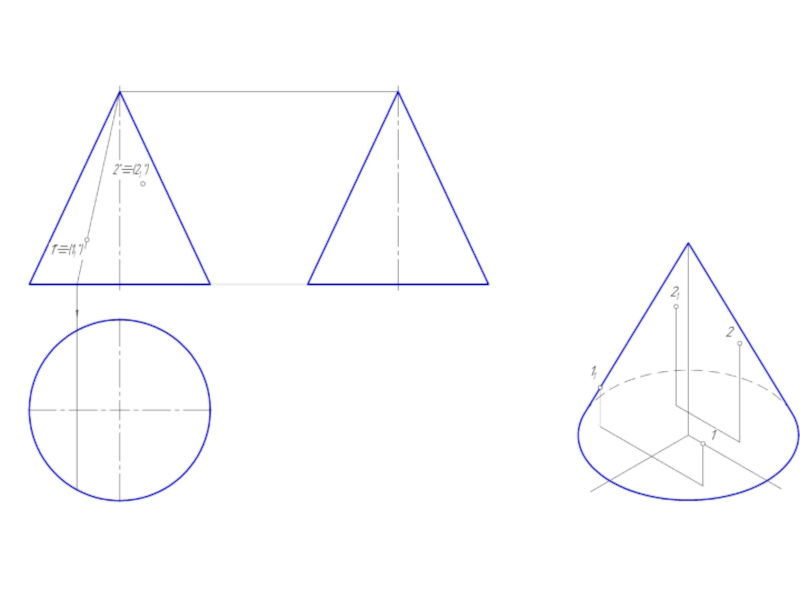
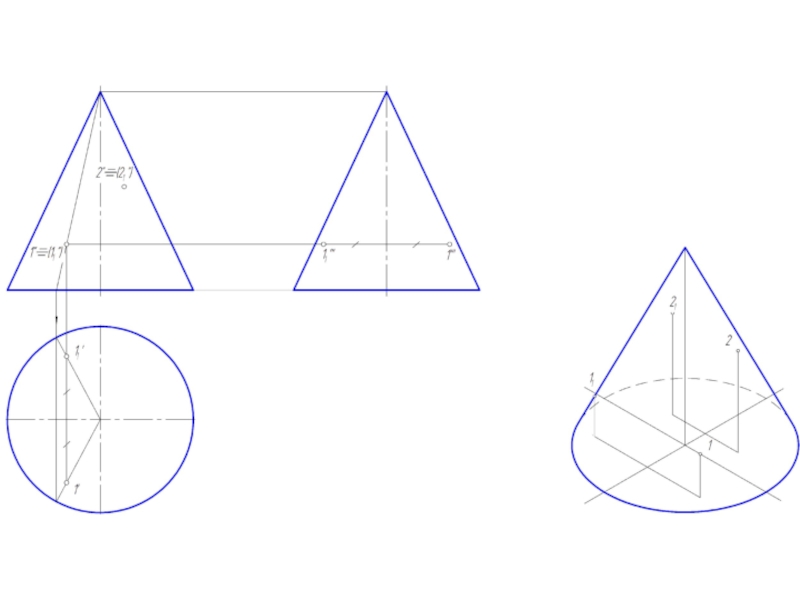
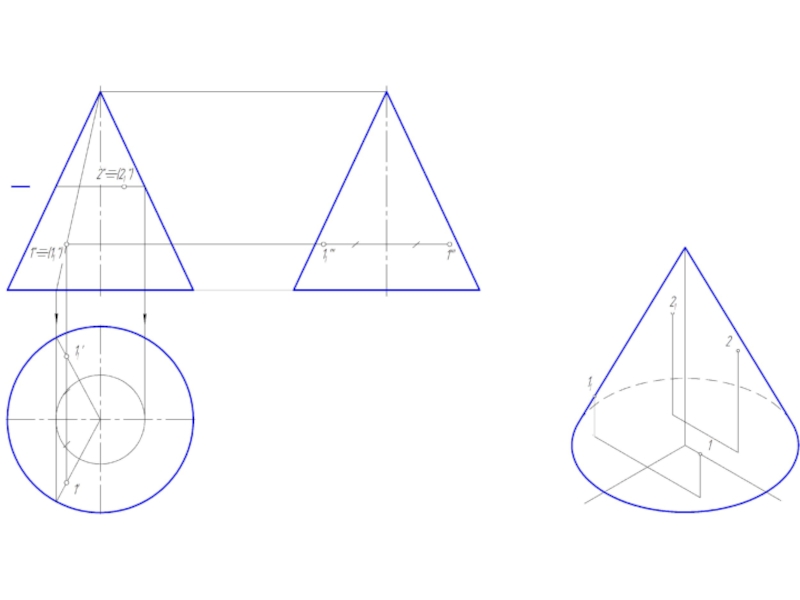
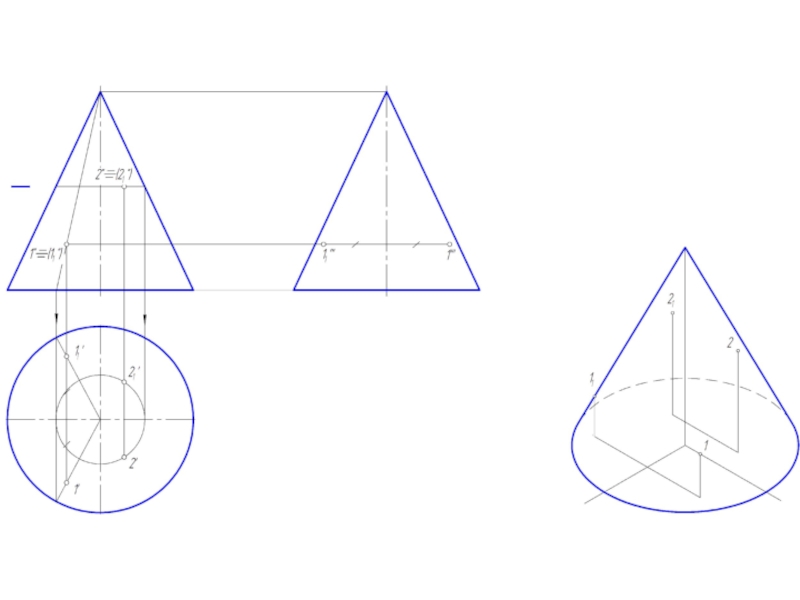
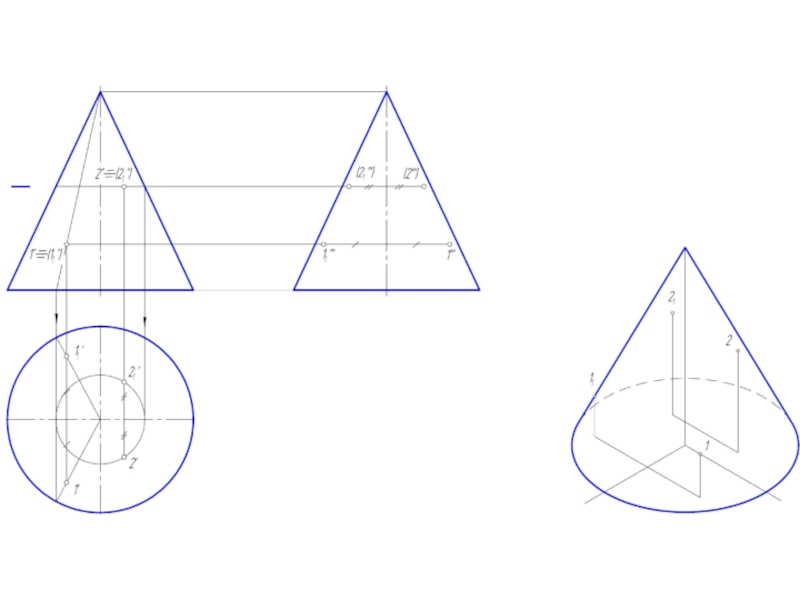
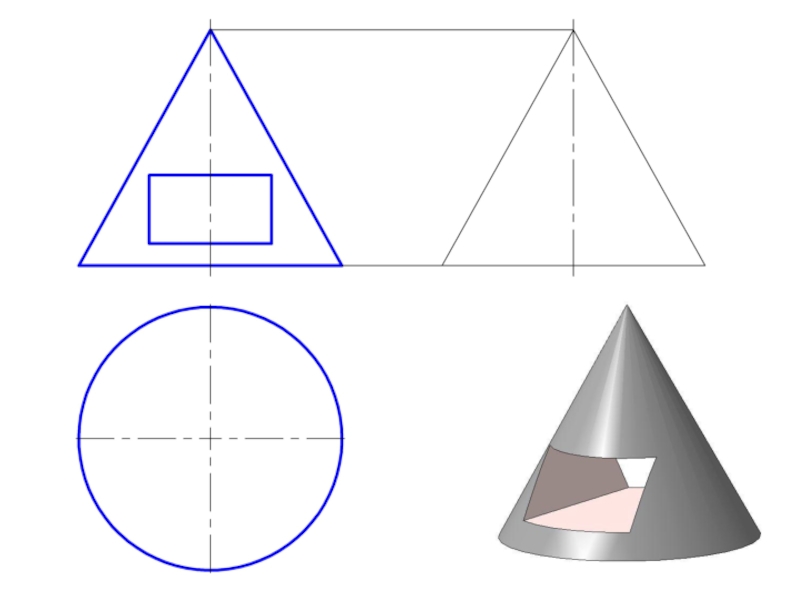
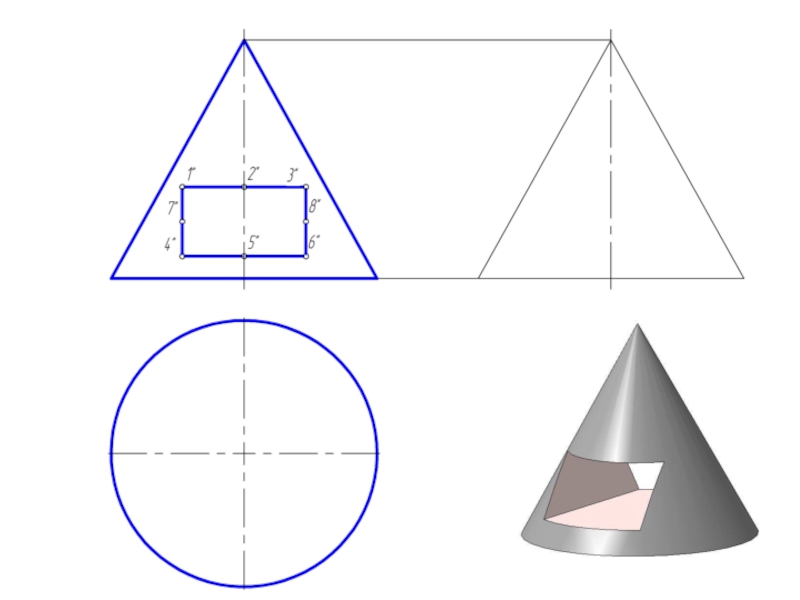
Слайд 2Точка на поверхности прямого кругового конуса
Точку, принадлежащую боковой поверхности конуса можно
найти двумя способами:
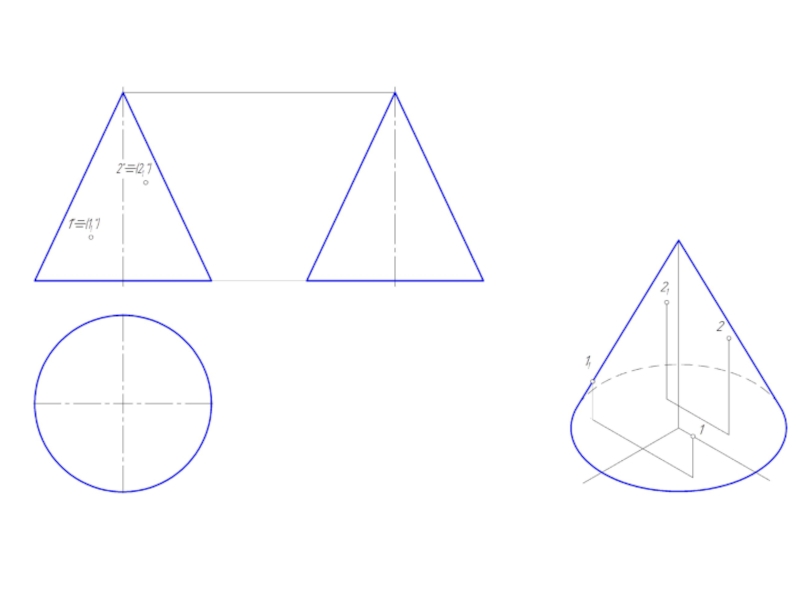
1. построить через проекцию искомой точки сечение конуса плоскостью, параллельной основанию конуса;
2. построить через проекцию искомой точки две прямые, проходящие через вершину конуса.
1. построить через проекцию искомой точки сечение конуса плоскостью, параллельной основанию конуса;
2. построить через проекцию искомой точки две прямые, проходящие через вершину конуса.
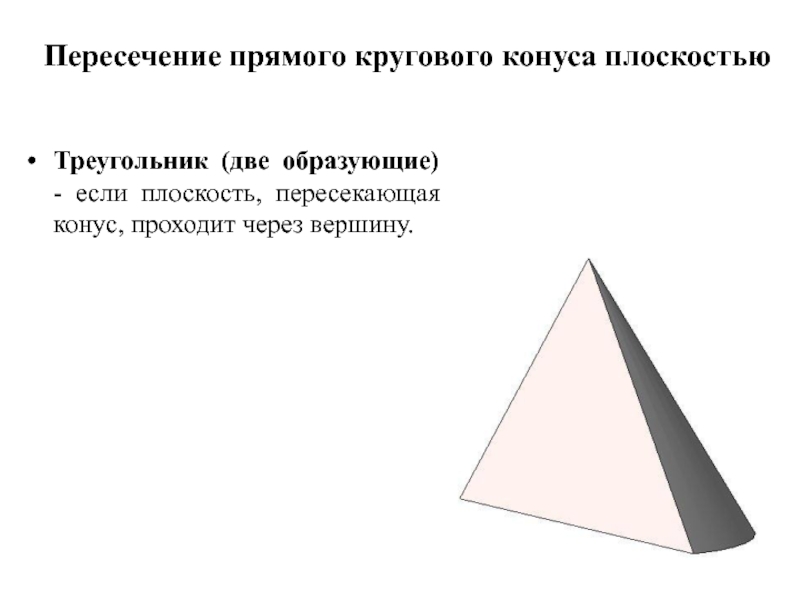
Слайд 11Пересечение прямого кругового конуса плоскостью
Треугольник (две образующие) - если плоскость, пересекающая
конус, проходит через вершину.
Слайд 12
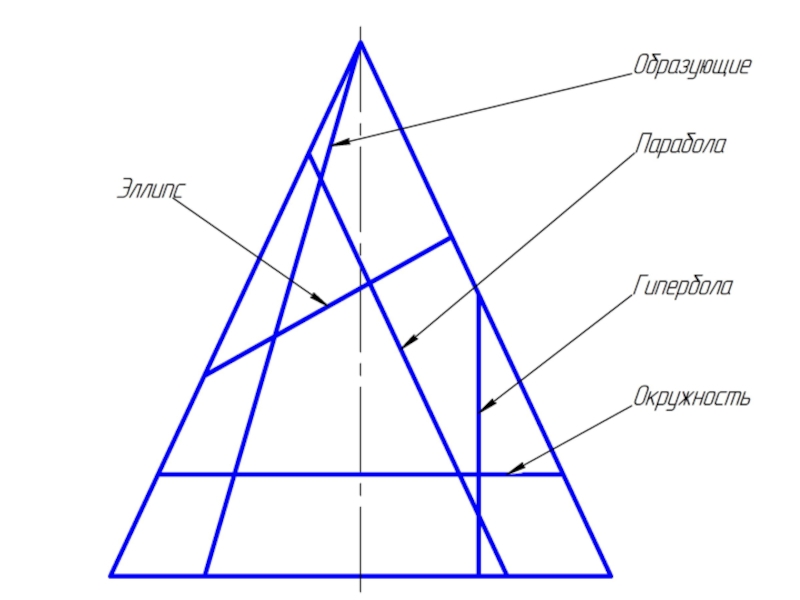
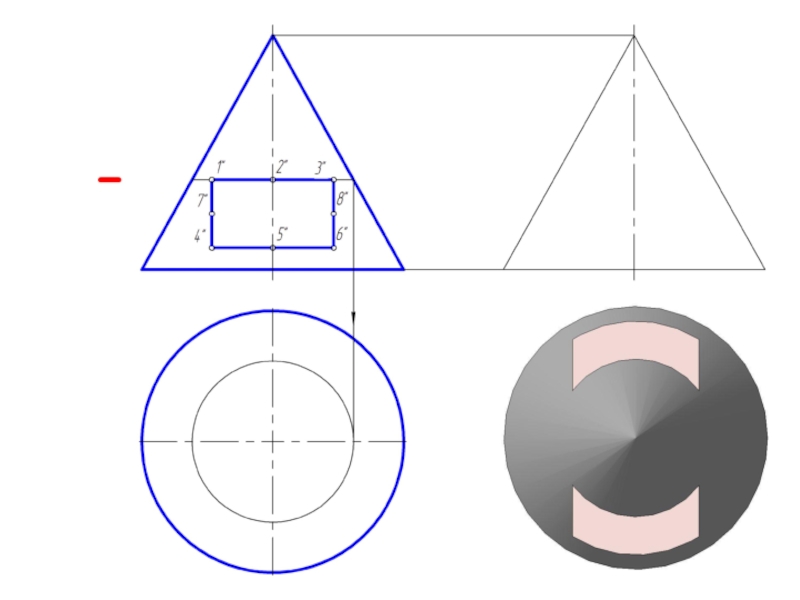
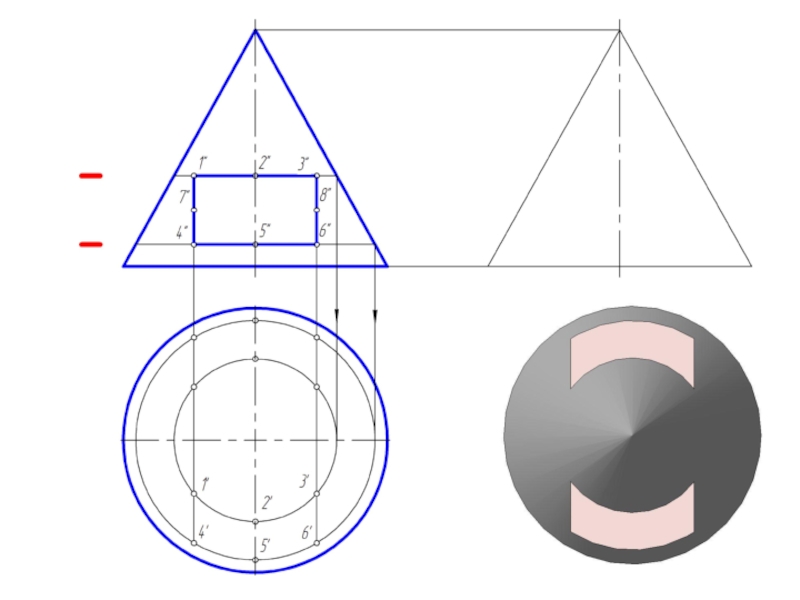
Если конус пересекается плоскостью, не проходящей через его вершину, то в
пересечении получается одна из следующих четырех кривых:
окружность – если секущая плоскость перпендикулярна оси конуса;
эллипс – если секущая плоскость пересекает все образующие (не параллельна ни одной из образующих конуса);
парабола – если секущая плоскость параллельна только одной из образующих;
гипербола – секущая плоскость параллельна двум образующим.
окружность – если секущая плоскость перпендикулярна оси конуса;
эллипс – если секущая плоскость пересекает все образующие (не параллельна ни одной из образующих конуса);
парабола – если секущая плоскость параллельна только одной из образующих;
гипербола – секущая плоскость параллельна двум образующим.
Слайд 27Пересечение прямого кругового конуса прямой линией
При определении точки пересечения прямой с
поверхностью в качестве вспомогательной секущей плоскости выбирают проецирующую плоскость.
Использование вспомогательной проецирующей плоскости не всегда упрощает решение и в некоторых случаях целесообразно применять плоскости общего положения.
В случае задачи по определению точки пересечения прямой общего положения с поверхностью прямого кругового конуса необходимо ввести вспомогательную плоскость, проходящую через эту прямую и вершину конуса, чтобы получить в пересечении прямые линии.
Использование вспомогательной проецирующей плоскости не всегда упрощает решение и в некоторых случаях целесообразно применять плоскости общего положения.
В случае задачи по определению точки пересечения прямой общего положения с поверхностью прямого кругового конуса необходимо ввести вспомогательную плоскость, проходящую через эту прямую и вершину конуса, чтобы получить в пересечении прямые линии.
Слайд 29
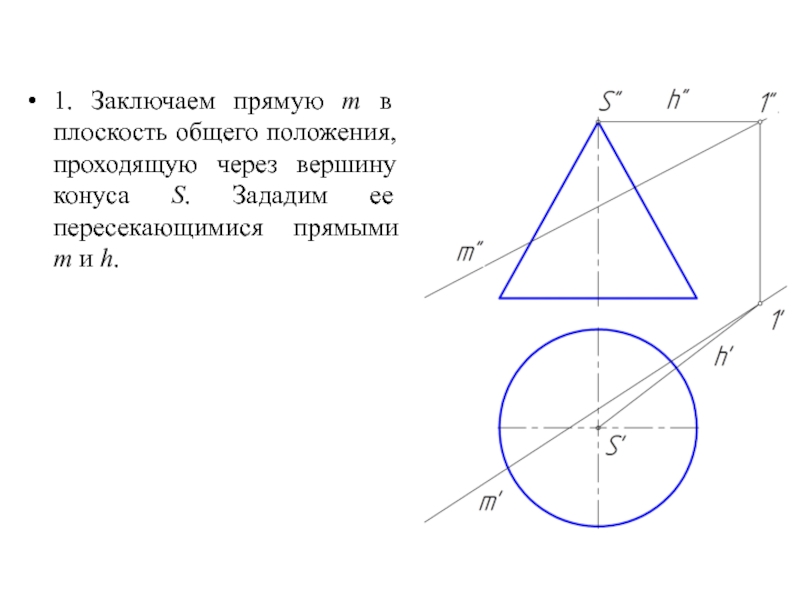
1. Заключаем прямую m в плоскость общего положения, проходящую через вершину
конуса S. Зададим ее пересекающимися прямыми
m и h.
Слайд 30
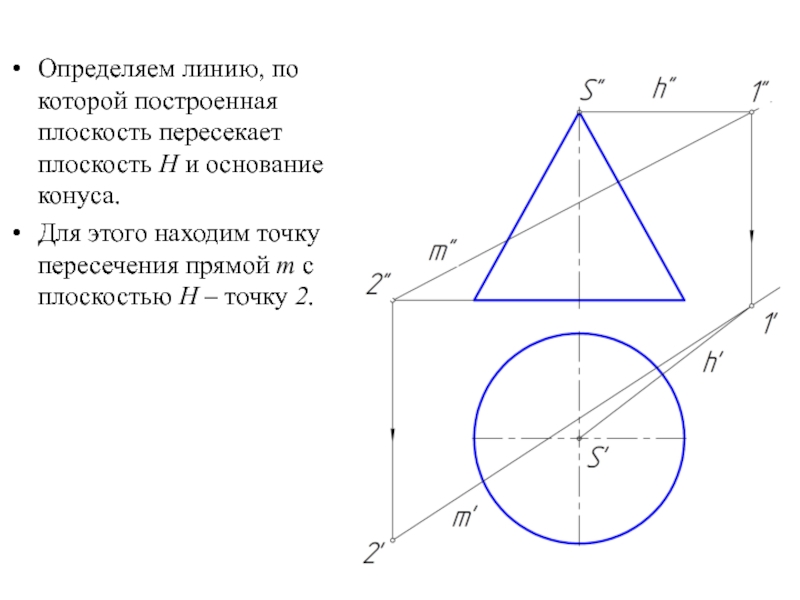
Определяем линию, по которой построенная плоскость пересекает плоскость H и основание
конуса.
Для этого находим точку пересечения прямой m с плоскостью Н – точку 2.
Для этого находим точку пересечения прямой m с плоскостью Н – точку 2.
Слайд 33
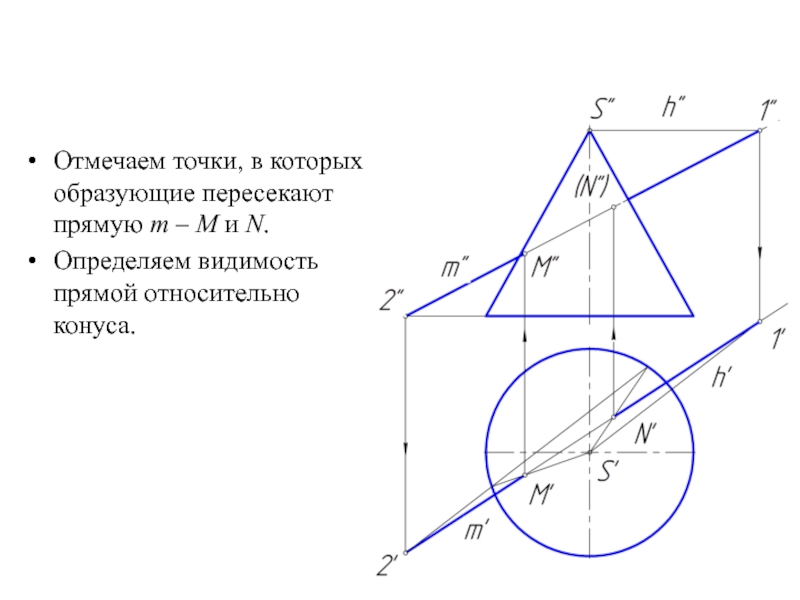
Отмечаем точки, в которых образующие пересекают прямую m – M и
N.
Определяем видимость прямой относительно конуса.
Определяем видимость прямой относительно конуса.