- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проверка статистических гипотез (лекция 9) презентация
Содержание
- 2. Критерий согласия Критерии согласия – это
- 3. Критерий χ2 (Пирсона) Критерий χ2 был предложен
- 4. Критерий χ2 (Пирсона) - продолжение Закон
- 5. Критерий χ2 (Пирсона) - продолжение Гипотеза
- 6. Критерий Колмогорова Мерой отличия эмпирической кривой
- 7. Критерий Колмогорова Недостатки методики: Учитывается
- 8. Критерий nω2 (Крамера – Мизеса – Смирнова)
- 9. Критерий nω2 (Крамера – Мизеса – Смирнова)
- 10. Критерии случайности Проверка гидрологических рядов
- 11. Критерий серий Серия – это всякий участок
- 12. Критерий общего числа серий Для проверки
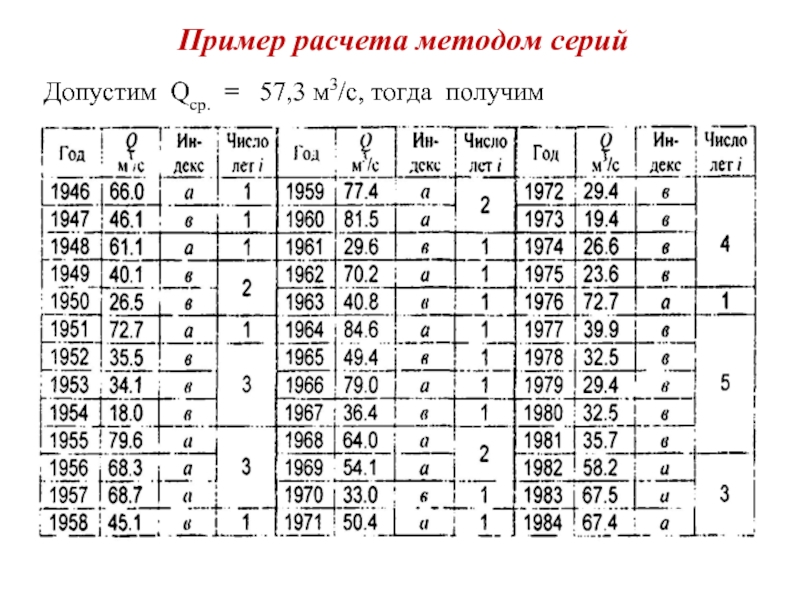
- 13. Пример расчета методом серий Допустим Qср. = 57,3 м3/с, тогда получим
- 14. Критерий наибольшей длины серий Этот критерий
- 15. Критерий числа повышений и понижений Пусть
- 16. Критерий числа экстремумов Экстремум – это
- 17. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1 Лекция 9 Проверка статистических гипотез Критерии согласия. Критерий χ2 (Пирсона). Критерий Колмогорова.
Слайд 2Критерий согласия
Критерии согласия – это статистики, которые позволяют проверить соответствие
Последовательность проверки:
- выдвигаются нулевая и альтернативная гипотезы
- назначается уровень значимости
- вычисляется эмпирическое значение тестовой статистики
- по результатам расчетов принимается решение
В качестве нулевой гипотезы принимается гипотеза о соответствие (согласии) аналитической и эмпирической функций распределения
Степень согласия оценивается с помощью специальных статистик
В гидрологической практике наиболее часто применяются критерий χ2 (Пирсона), критерий Колмогорова и критерий nω2 (Крамера – Мизеса – Смирнова).
Слайд 3Критерий χ2 (Пирсона)
Критерий χ2 был предложен в начале XX Карлом Пирсоном
Последовательность применения:
Область допустимых значений (ОДЗ) исследуемой СВ Х разбивается на k интервалов. Число интервалов можно рассчитать по формуле k ≈ 5lg (n)
Интервалы по оси Х не будут равновеликими, но зато вероятность попадания значения СВ Х в любой интервал будет одинаковой p = 1/k
Теоретическое число случаев попадания значения СВ Х в каждый интервал будет равно m = n/k (n – длина выборки)
Расхождение между эмпирическими данными и аналитической функцией распределения определяется по тестовой статистике
где р* и рi – соответственно эмпирическая и теоретическая вероятность попадания значения СВ в i – й интервал; n – длина выборки; k – число интервалов.
Слайд 4Критерий χ2 (Пирсона) - продолжение
Закон распределения данной статистики не зависит
где r – число параметров исходного распределения, определяемых по эмпирическим данным
Учитывая, что p*= m*/n можно записать, что
где m* и m – соответственно эмпирическое и теоретическое число случаев попадания значения СВ Х в i- тый интервал.
В итоге получим, что
Слайд 5Критерий χ2 (Пирсона) - продолжение
Гипотеза о соответствии (согласии) эмпирической и
Критерий χ2 может быть применен при выяснении вопроса о лучшем соответствии одной из нескольких аналитических кривых распределения одному и тому же эмпирическому ряду. При этом меньшее значение χ2 будет свидетельствовать о лучшем соответствии данной функции распределения эмпирическим данным
Принято считать, что критерий согласия χ2 допустимо применять при n > 50. При этом желательно, чтобы число интервалов было равно 8-12 и в каждом разряде было не менее 5 элементов.
Из предыдущего выражения видно, что чем больше значение статистики χ2, тем больше расхождение между эмпирической и аналитической кривыми. Поэтому при использовании критерия χ2 (Пирсона) назначают односторонний уровень значимости (обычно α=5% или α=10%).
Слайд 6Критерий Колмогорова
Мерой отличия эмпирической кривой распределения от теоретической является абсолютное
∆ = max [Р*(х) - Р(х)]
Последовательность вычисления
1. Для каждого значения СВ Х вычисляются Р*(х), Р(х) и их разности
2. Выбирается наибольшее по модулю разность ∆
3. Рассчитывается статистика λ* = ∆√n, где n – объем выборки.
4. Функция обеспеченностей статистики λ при достаточно больших значениях n (n>40) может аппроксимирована выражением
Координаты этой функции представлены в таблицах
5. Если значение Р(λ*) больше принятого уровня значимости, то гипотеза о соответствии эмпирической и аналитической функций распределения не опровергается
Слайд 7Критерий Колмогорова
Недостатки методики:
Учитывается только максимальное расхождение между эмпирической и
Наибольшая разность ∆ обычно отмечается в средней части кривой распределения, в то время как в гидрологической практике чаще всего важно знать ее крайние левые и правые части
Критерий не учитывает числа параметров, входящих в теоретическую функцию распределения
Слайд 8Критерий nω2 (Крамера – Мизеса – Смирнова)
Тестовой статистикой данного критерия
где Р(х) – рассчитывается по формуле pm = ((m-0.5)100%)/n
Для расчета Р(х) можно использовать формулу pm = (100m)/(n+1)
В этом случае выражение для тестовой статистики примет вид
При n>40 распределение статистики nω2 не зависит от вида исходного теоретического распределения и близко к некоторому предельному распределению, показанному ниже в таблице
Слайд 9Критерий nω2 (Крамера – Мизеса – Смирнова) - 2
Если эмпирическое значение
оказывается больше теоретического значения nω2 при уровне значимости α%, то гипотеза о соответствии эмпирической и аналитической функций обеспеченностей опровергается.
Слайд 10Критерии случайности
Проверка гидрологических рядов на случайность проводится в рамках
Применение критериев случайности основано на сопоставлении конкретных статистик эмпирического ряда с соответствующими теоретическими статистиками случайных совокупностей
Слайд 11Критерий серий
Серия – это всякий участок последовательности, состоящий из элементов одного
Длина серии – число элементов, входящих в серию
К серии из элементов а относятся члены последовательности, значения которых превышают выборочное среднее (или медианное) значение
К серии из элементов в относятся члены последовательности, значения которых меньше выборочного среднего (или медианного) значения
Слайд 12Критерий общего числа серий
Для проверки гипотезы о том, что данная
Для случайных совокупностей статистика R = ra + rв имеет нормальное распределение с параметрами
Исходя из этого, задавшись уровнем значимости α, можно построить для R доверительный интервал
где t1-α – квантиль стандартного нормального распределения (по таблице)
Если значение R*, определенное по выборке, попадает в этот интервал, то гипотеза о случайности данной совокупности не опровергается.
Слайд 14Критерий наибольшей длины серий
Этот критерий использует в качестве тестовой статистики
Теоретически доказано, что для СВ значение K выражается формулой
где α – вероятность (в долях единицы), с которой в выборке объемом n можно встретить хотя бы одну серию из элементов a и в длиной K и более.
При проверке нулевой гипотезы о случайности выборки эмпирическое значение статистики K* сравнивается с теоретическим, рассчитанным по вышепоказанной формуле
при уровне значимости α. Гипотеза не опровергается, если K*< K.
Слайд 15Критерий числа повышений и понижений
Пусть имеется выборка СВ Х: х1,
Переход от xi-1 к xi, называется повышением и обозначается «+», если xi-1 < xi,
Переход от xi-1 к xi, называется понижением и обозначается « - «, если xi-1 > xi,
Для случайных последовательностей число повышений и понижений распределяется асимптотически нормально с параметрами
Задавшись уровнем значимости α и учитывая, что математические ожидание и дисперсии числа повышений и понижений равны, можно построить доверительный интервал
где k – число повышений (k+) или (k-) в исследуемой выборке; t’1- α – квантиль нормального стандартного распределения
Если эмпирические значения k*+ или k *-. попадают в доверительный интервал, гипотеза о случайности выборки не опровергается
m – t’1-α√D < k < m + t’1-α√D
Слайд 16Критерий числа экстремумов
Экстремум – это элемент последовательности х1, х2, х3
Для выборок, представляющих собой последовательности независимых значений СВ, число экстремумов распределено асимптотически нормально с параметрами
Проверка гипотезы о случайности ряда производиться так же, как в предыдущем случае