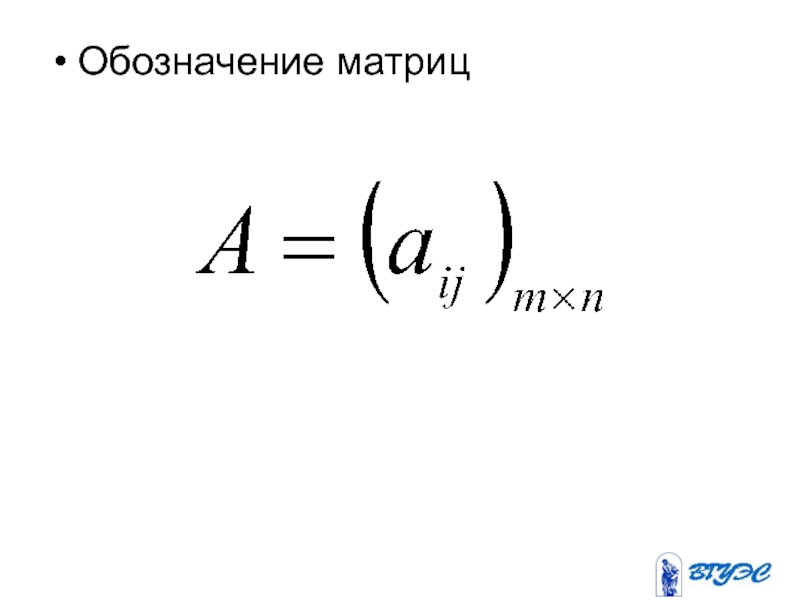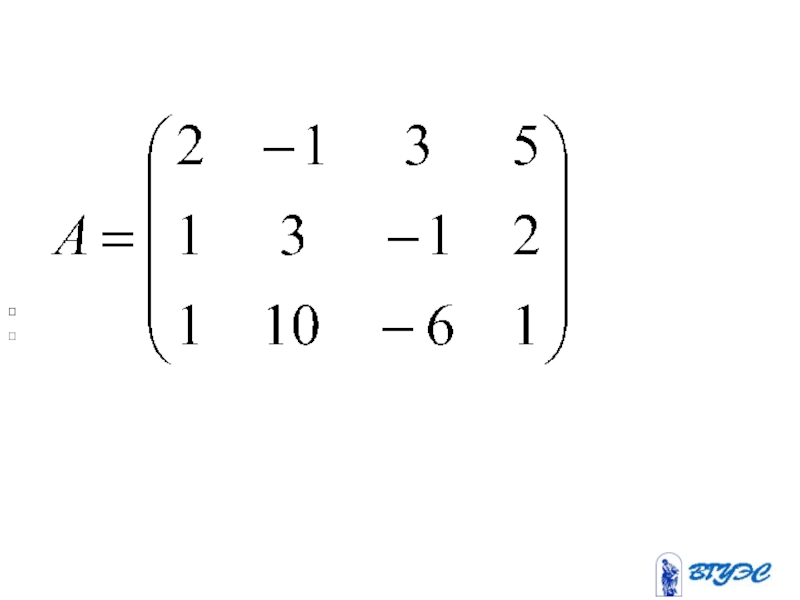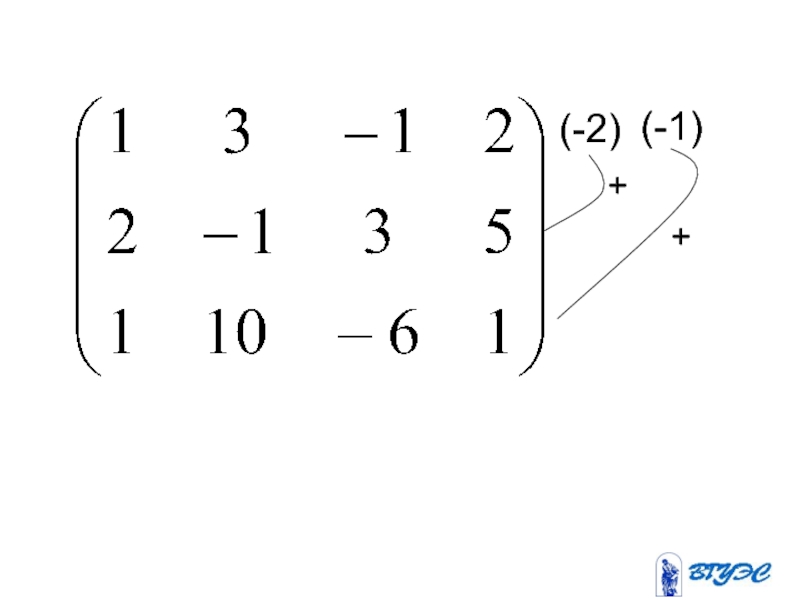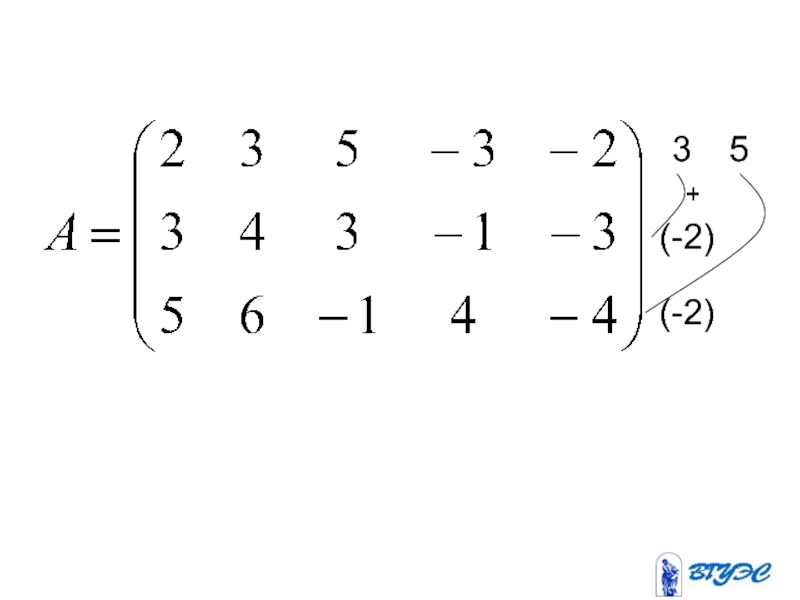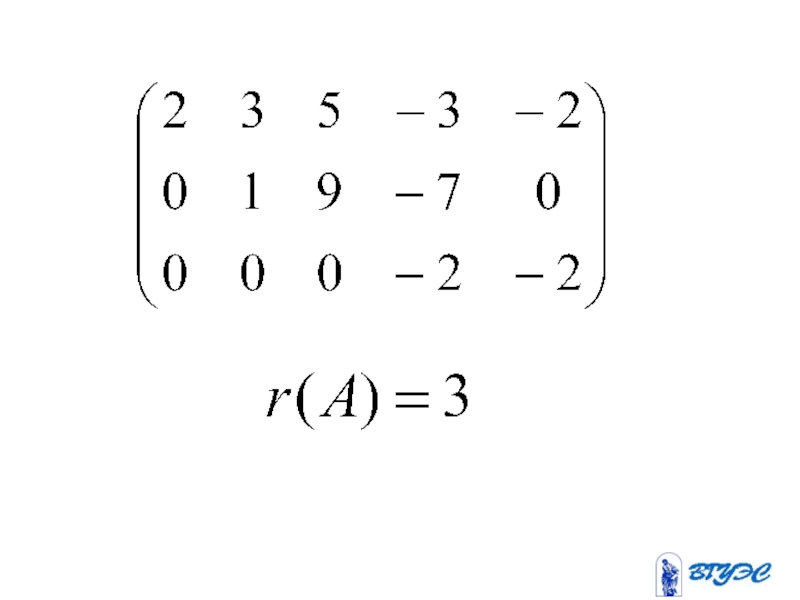- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Матрицы. Обозначение матриц презентация
Содержание
- 1. Матрицы. Обозначение матриц
- 2. Матрицей называется прямоугольная таблица чисел .
- 4. Обозначение матриц
- 5. Матрица размера m×m называется квадратной.
- 6. Две матрицы считаются равными, если равны их
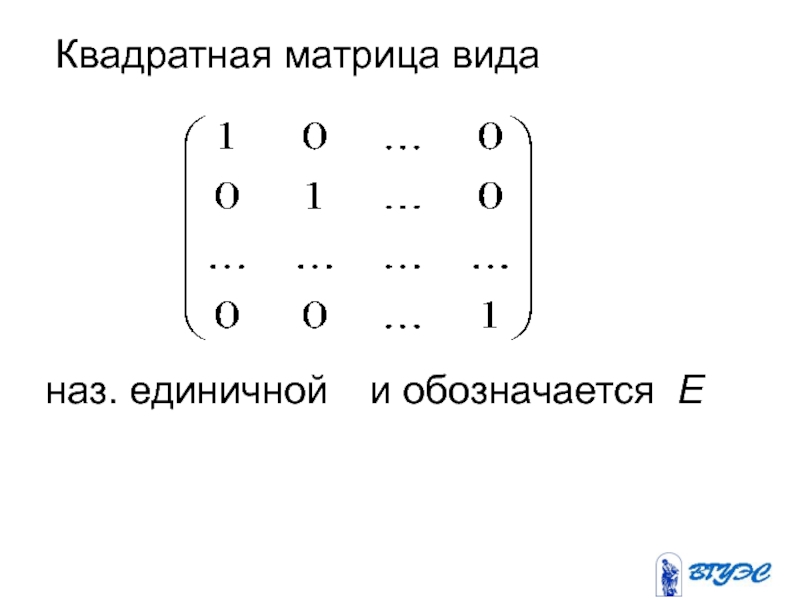
- 7. Квадратная матрица вида
- 8. Матрица, все элементы которой равны нулю, наз.
- 9. Матрица наз. транспонированной по отношению к матрице
- 10. Действия над матрицами. Суммой двух матриц одинаковой
- 11. Произведением матрицы
- 12. Разностью двух
- 13. Произведением матрицы размера
- 14. Свойства операций над матрицами
- 17. Если и
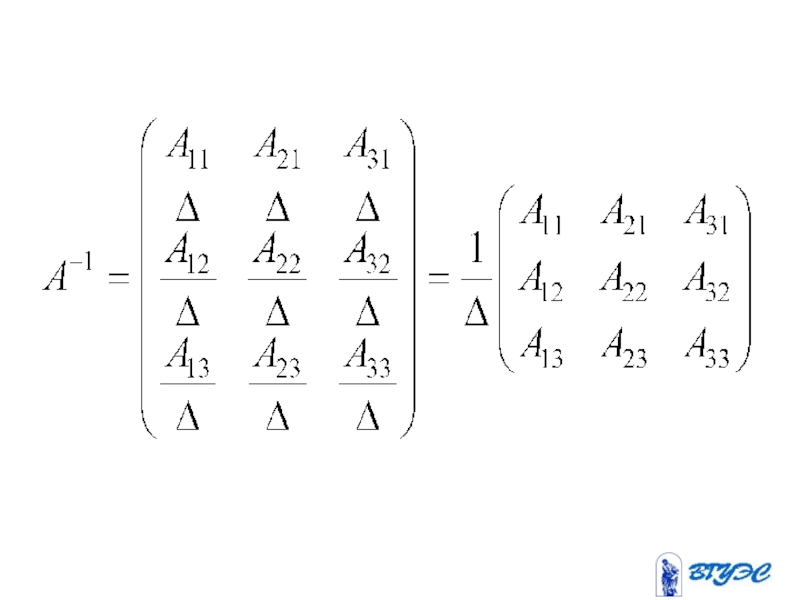
- 18. Обратная матрица
- 19. Пусть - квадратная матрица. Обратной
- 20. Для того, чтобы квадратная матрица
- 22. Р а н г м а
- 23. Теорема о ранге матрицы Ранг матрицы
- 24. Элементарные преобразования матрицы. 1.Умножение всех элементов строк
- 25. 4.Отбрасывание одной из
- 26. Теорема: Элементарные преобразования не меняют ранг
- 27.
- 28. (-2) (-1) + +
- 29. +
- 31. 3 (-2) + 5 (-2)
- 32. (-3) +
Матрицей называется прямоугольная таблица чисел . Если матрица содержит строк и столбцов, то говорят, что матрица имеет размерность
Слайд 2
Матрицей называется прямоугольная
таблица чисел .
Если матрица содержит
строк и
столбцов, то говорят, что матрица имеет
размерность .
- порядок матрицы
столбцов, то говорят, что матрица имеет
размерность .
- порядок матрицы
Слайд 5 Матрица размера m×m называется
квадратной.
Матрица , имеющая только одну
строку
называется матрицей-строкой.
Матрица, имеющая только один
столбец называется
матрицей-столбцом .
называется матрицей-строкой.
Матрица, имеющая только один
столбец называется
матрицей-столбцом .
Слайд 6Две матрицы считаются равными,
если равны их размеры и равны
элементы, стоящие на
одинаковых
местах.
Квадратная матрица называется
невырожденной (неособенной), если
её определитель отличен от нуля, и
вырожденной (особенной) , если
определитель её равен нулю.
местах.
Квадратная матрица называется
невырожденной (неособенной), если
её определитель отличен от нуля, и
вырожденной (особенной) , если
определитель её равен нулю.
Слайд 8Матрица, все элементы которой равны нулю, наз. нулевой.
Определитель, составленный из элементов
квадратной матрицы, наз. определителем матрицы.
Очевидно
Очевидно
Слайд 10Действия над матрицами.
Суммой двух матриц одинаковой
размерности А и В называется
матрица С
той же размерности,
элементы которой равны суммам
элементов матриц A и B с
одинаковыми индексами.
элементы которой равны суммам
элементов матриц A и B с
одинаковыми индексами.
Слайд 11
Произведением матрицы на
число α называется
матрица ,
получающаяся из матрицы A
умножением всех её элементов
на α .
получающаяся из матрицы A
умножением всех её элементов
на α .
Слайд 13 Произведением матрицы
размера на
матрицу
размера
называется матрица размера
, элемент которой , стоящий в i-ой строке и j-ом столбце, равен
сумме произведений элементов i-ой
строки матрицы A и соответствующих
элементов j-го столбца матрицы B.
размера
называется матрица размера
, элемент которой , стоящий в i-ой строке и j-ом столбце, равен
сумме произведений элементов i-ой
строки матрицы A и соответствующих
элементов j-го столбца матрицы B.
Слайд 19Пусть - квадратная матрица.
Обратной для неё матрицей наз.
квадратная матрица
того же порядка,
обозначаемая и
удовлетворяющая условию
обозначаемая и
удовлетворяющая условию
Слайд 20Для того, чтобы квадратная
матрица имела
обратную
матрицу, необходимо и достаточно,
чтобы матрица была
невырожденной.
матрицу, необходимо и достаточно,
чтобы матрица была
невырожденной.
Слайд 22Р а н г м а т р и ц
ы
Рангом матрицы называется наивысший
из порядков отличных от нуля миноров
матрицы.
Ранг матрицы A обозначается:
или .
Слайд 23Теорема о ранге матрицы
Ранг матрицы равен
максимальному числу линейно –
независимых строк матрицы.
Слайд 24Элементарные преобразования матрицы.
1.Умножение всех элементов строк на одно и то же
число не равное 0.
2. Перестановка строк местами.
3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и тоже число.
2. Перестановка строк местами.
3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и тоже число.
Слайд 26
Теорема: Элементарные
преобразования не меняют ранг
матрицы.
Матрицы, полученные с помощью
элементарных
преобразований
наз. эквивалентными (~).
наз. эквивалентными (~).
