- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Простейшие задачи в координатах презентация
Содержание
- 1. Простейшие задачи в координатах
- 2. Найти координаты точек А, В, С и
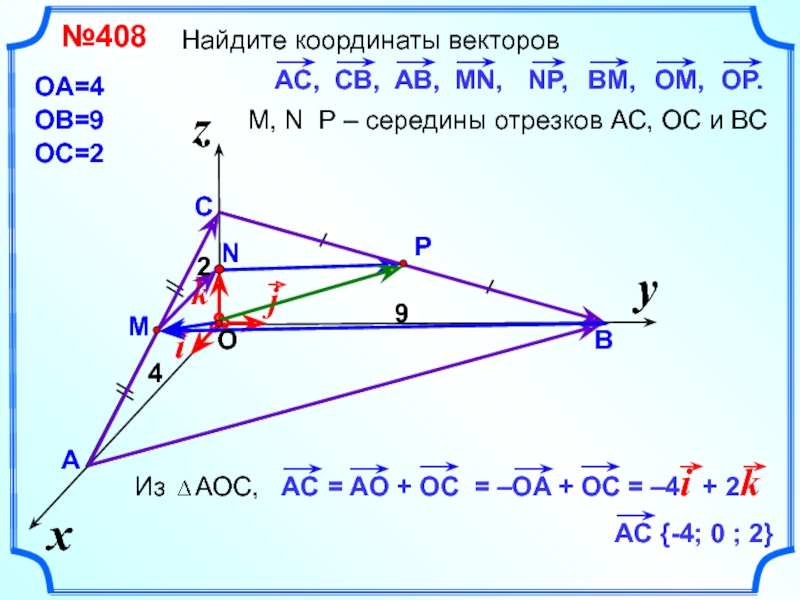
- 3. Найдите координаты векторов y x
- 4. -2f{ }
- 5. –i{ }
- 6. a +c {
- 7. Два ненулевых вектора
- 8. Два ненулевых вектора
- 9. * * -12 0 *
- 10. Векторы называются компланарными, если
- 11. Любые два вектора компланарны. Три вектора, среди которых имеются два коллинеарных, также компланарны. Признак компланарности
- 12. Компланарны ли векторы
- 13. Компланарны ли векторы
- 14. Компланарны ли векторы
- 15. x z y
- 16. B A (3;5;7), (5;4;-1), P C (2;-1;0),
- 17. Найдите координаты векторов R(2; 7;1)
- 18. { }
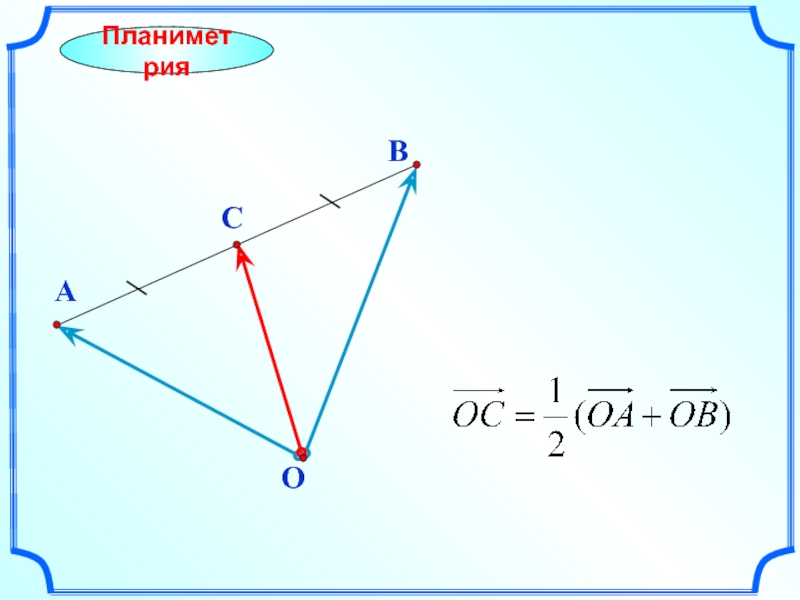
- 19. B Планиметрия A
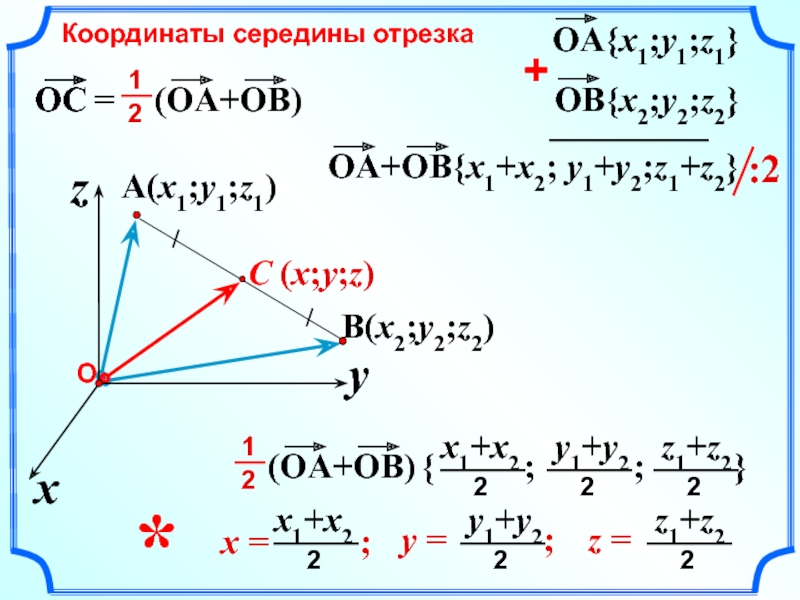
- 20. C (x;y;z) A(x1;y1;z1) Координаты
- 21. A(x1;y1;z1) x
- 22. -1 ( ; ;
- 23. Найдите координаты середины отрезков R(2;7;4);
- 24. (
- 25. Дано:
- 26. x z y
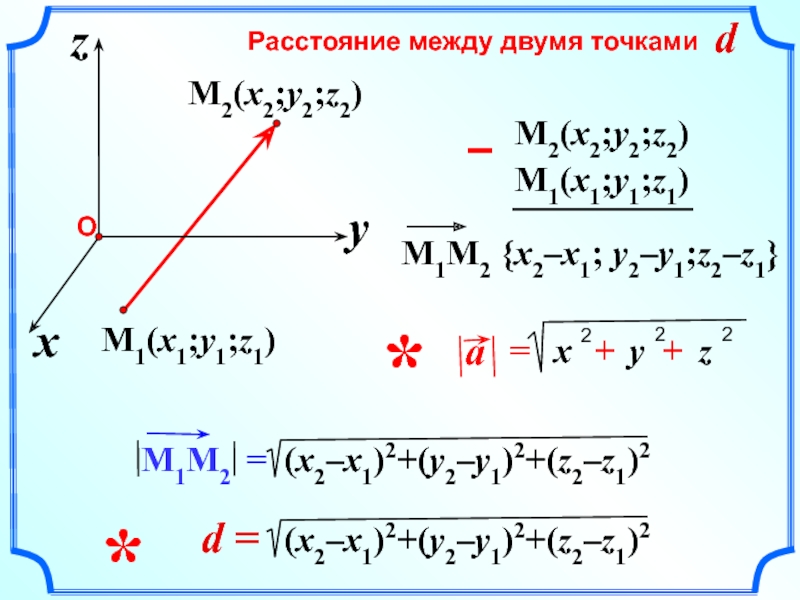
- 27. Расстояние между двумя точками d
- 28. № 426 (a) Найдите длину
- 29. № 426 (б) Найдите длину
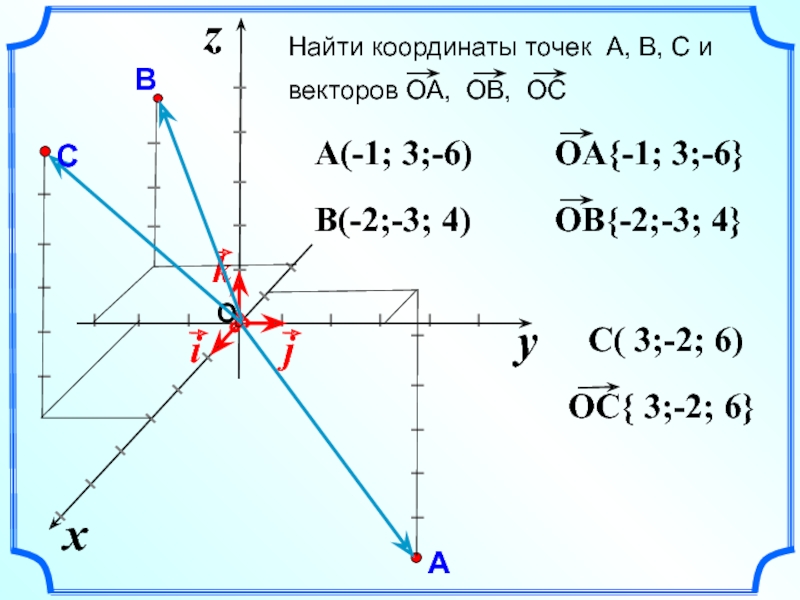
Слайд 2Найти координаты точек А, В, С и
векторов ОА, ОВ, ОС
A(-1; 3;-6)
B(-2;-3; 4)
y
x
z
I I I I I I I I
I I I I I
I I I I I I I I
O
C( 3;-2; 6)
Слайд 4-2f{ }
-c{ }
-3d{
Найти координаты векторов.
Вводите ответы в текстовые поля, не делая пробелов
Слайд 5–i{ }
-d{ }
-b{
-a{ }
Найти координаты векторов,
противоположных данным.
Вводите ответы в текстовые поля, не делая пробелов
Слайд 6a +c { }
a - c{
b+d{ }
c +e{ }
f - d{ }
b - d{ }
Найти координаты векторов.
Вводите ответы в текстовые поля, не делая пробелов
d{-2;-3;-1};
b{-2; 0; 4};
c {2;-5; 4};
e {2;-3;-9};
d{-2;-3;-4};
Слайд 7
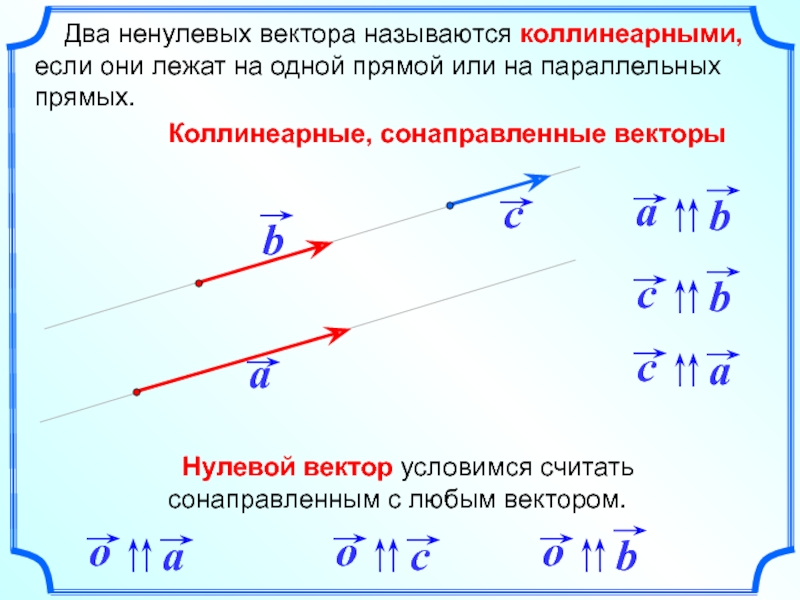
Два ненулевых вектора называются коллинеарными, если они лежат на
Коллинеарные, сонаправленные векторы
Нулевой вектор условимся считать сонаправленным с любым вектором.
Слайд 8
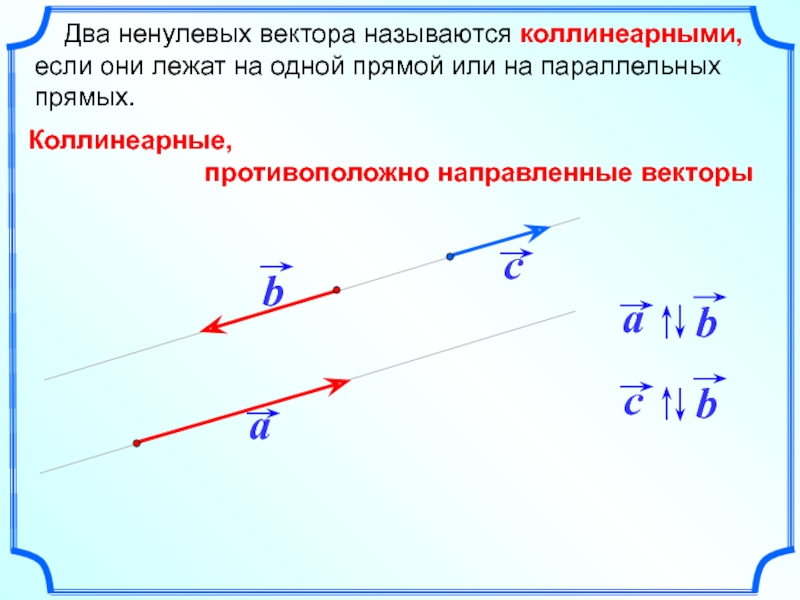
Два ненулевых вектора называются коллинеарными, если они лежат на
Коллинеарные,
противоположно направленные векторы
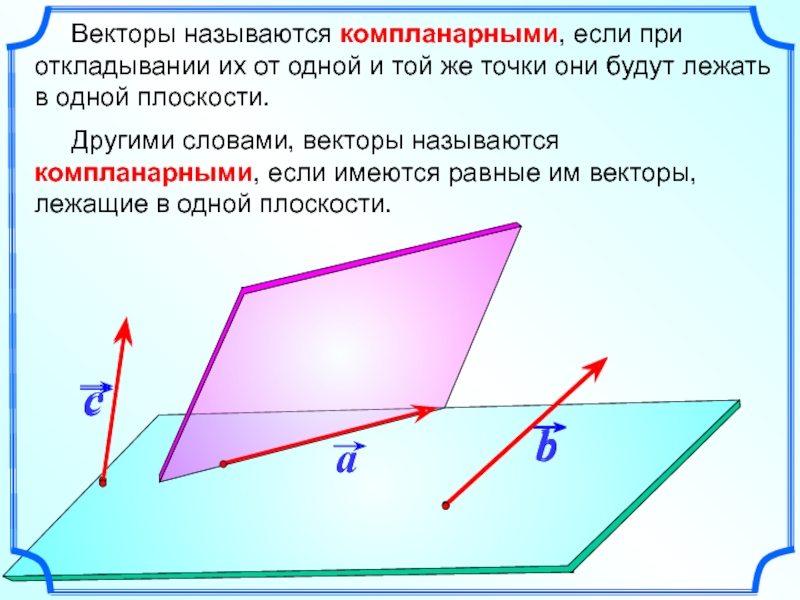
Слайд 10 Векторы называются компланарными, если при откладывании их от
Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Слайд 11Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также
Признак компланарности
Слайд 12Компланарны ли векторы
2
6
-3
6
18
-9
Нулевой вектор коллинеарен любому вектору.
Значит, эти векторы компланарны.
Слайд 15
x
z
y
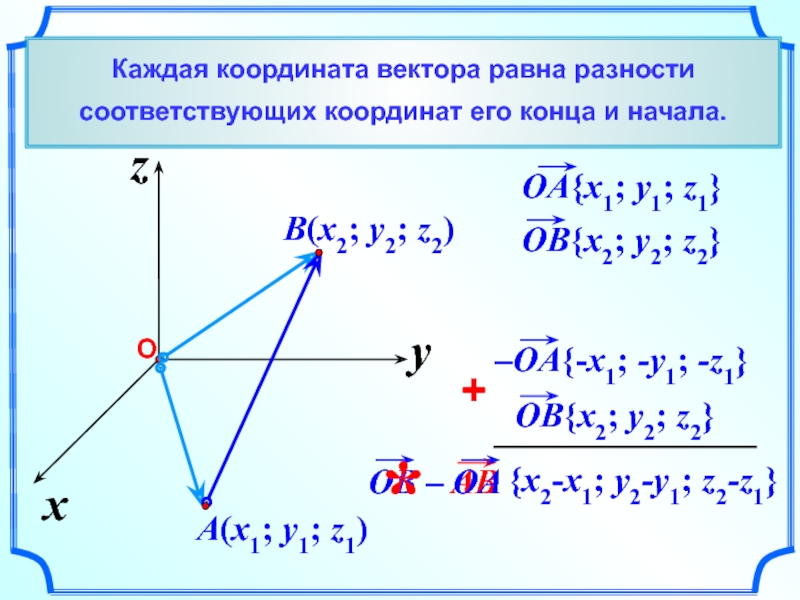
{x2-x1; y2-y1; z2-z1}
Каждая координата вектора равна разности
соответствующих координат его конца
*
Слайд 16B
A
(3;5;7),
(5;4;-1),
P
C
(2;-1;0),
(4;-4;2),
D
(-3;-4;0),
R
T
(-4;0;-4),
(0;5;-1),
N
(3;2;-3),
B(5;4;-1)
A(3;5;7)
C(4;-4;2)
P(2;-1;0)
T(0; 5;-1)
R(-4;0;-4)
O
(0;0;0),
O
(0;0;0),
AB
ON
Слайд 17
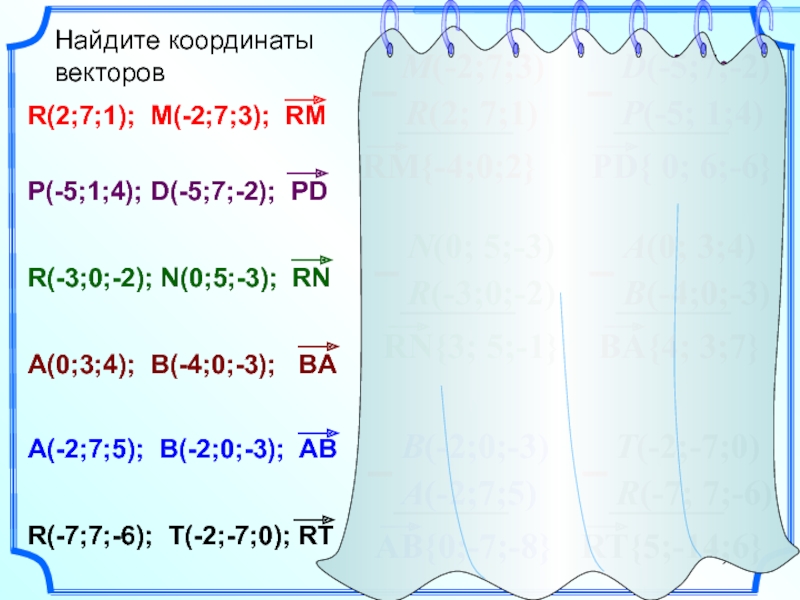
Найдите координаты
векторов
R(2; 7;1)
M(-2;7;3)
R(2;7;1); M(-2;7;3); RM
P(-5;1;4); D(-5;7;-2); PD
P(-5; 1;4)
D(-5;7;-2)
R(-3;0;-2); N(0;5;-3); RN
A(0;3;4);
R(-7;7;-6); T(-2;-7;0); RT
A(-2;7;5); B(-2;0;-3); AB
R(-3;0;-2)
N(0; 5;-3)
B(-4;0;-3)
A(0; 3;4)
A(-2;7;5)
B(-2;0;-3)
R(-7; 7;-6)
T(-2;-7;0)
Слайд 18{ }
Найти координаты векторов.
Вводите ответы в текстовые поля, не делая пробелов
{ }
{ }
{ }
{ }
{ }
Слайд 21A(x1;y1;z1)
x
z
y
B(x2;y2;z2)
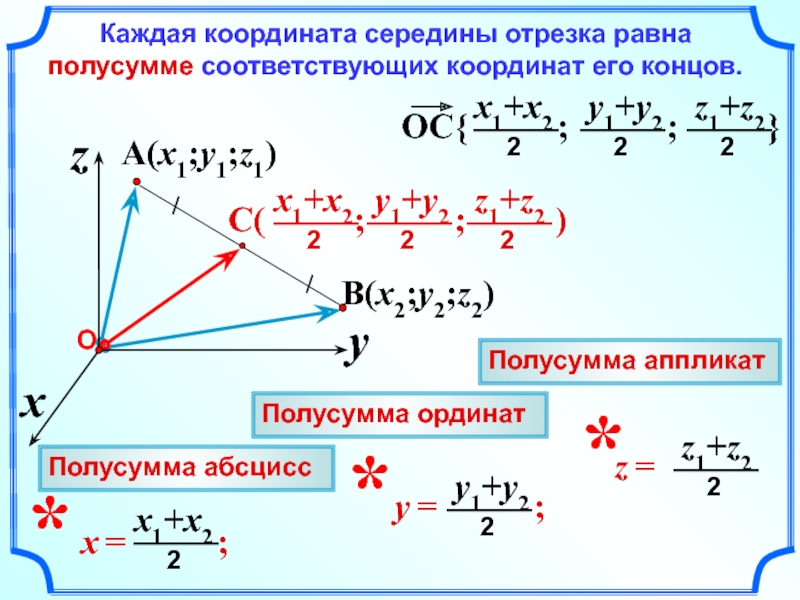
Каждая координата середины отрезка равна полусумме соответствующих
Полусумма абсцисс
Полусумма ординат
Полусумма аппликат
*
*
*
Слайд 22-1
( ; ; )
A(0; 3;-4),
B(-2;2;0), середина –
M
Полусумма абсцисс
Полусумма ординат
Полусумма аппликат
2,5
-2
= -1
= 2,5
= -2
№ 424 (a) Найдите координаты середины отрезка
Слайд 23
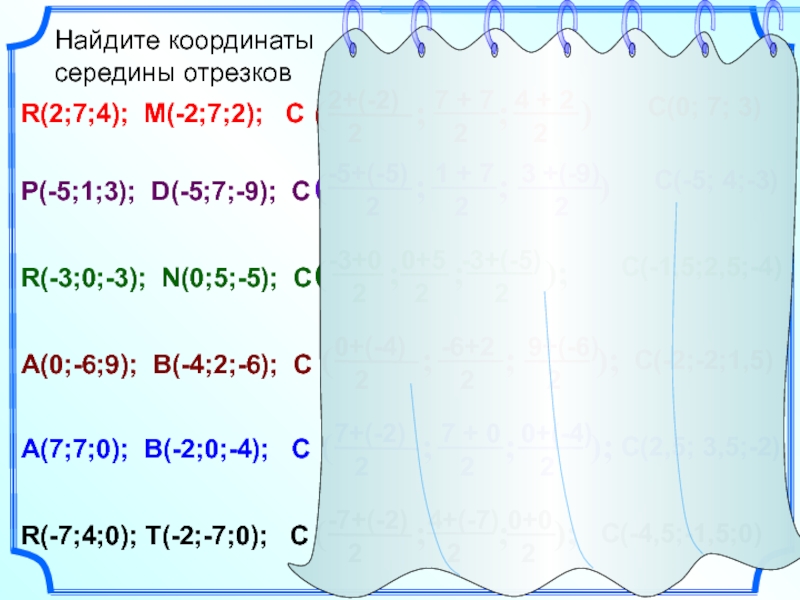
Найдите координаты
середины отрезков
R(2;7;4); M(-2;7;2); C
P(-5;1;3); D(-5;7;-9); C
R(-3;0;-3);
A(0;-6;9); B(-4;2;-6); C
R(-7;4;0); T(-2;-7;0); C
A(7;7;0); B(-2;0;-4); C
Слайд 24( )
(
( )
( )
( )
( )
Найти координаты середин отрезков.
Вводите ответы в текстовые поля, не делая пробелов.
R(2;7;4); M(-2;7;2); C
P(-5;1;3); D(-5;7;-9); C
R(-3;0;-3); N(0;5;-5); C
A(0;-6;9); B(-4;2;-6); C
R(-7;4;0); T(-2;-7;0); C
A(7;7;0); B(-2;0;-4); C
Слайд 25Дано:
Найти:
A(5; 4; -6);
C(-3;
B(a; b;c)
Обратная задача.
x
x1
y
x2
y1
y2
– 6 = 5 + a
a = – 11
4 = 4 + b
b = 0
B(-11; 0;26)
z2
z1
z
20 = -6 + c
c = 26
Слайд 26
x
z
y
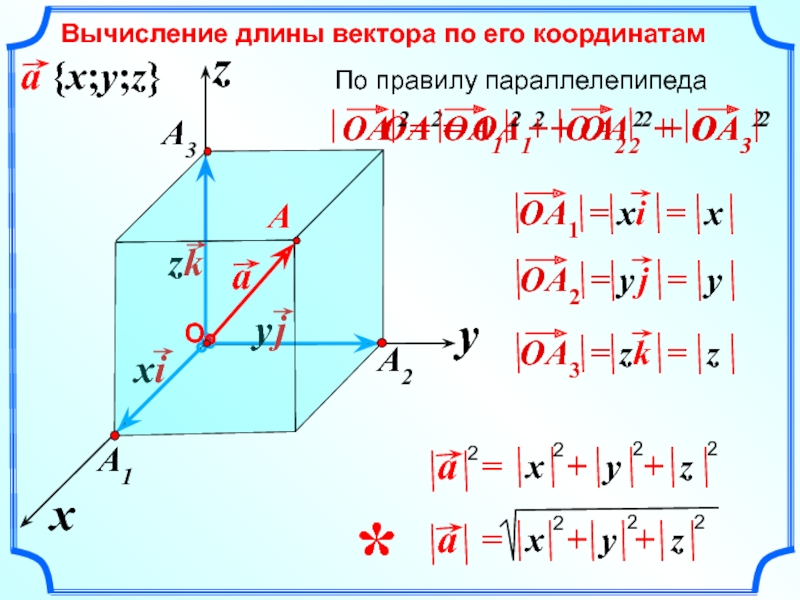
Вычисление длины вектора по его координатам
OA2= OA12 + OA22 + OA32
По правилу параллелепипеда
=
=
=
*
Слайд 28№ 426 (a) Найдите длину вектора АВ
A(-1;0;2) и
1 способ
2 способ
1)
2)
B(1;-2;3)
A(-1;0;2)
= 3
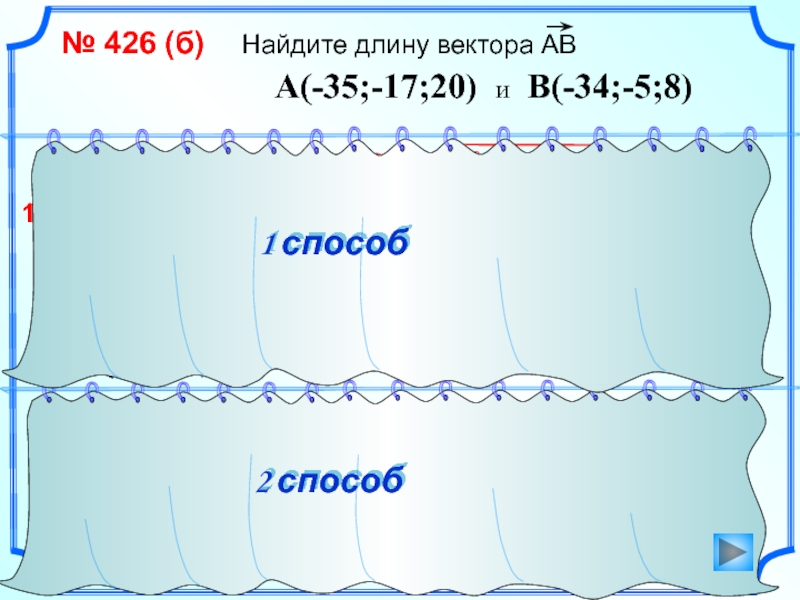
Слайд 29№ 426 (б) Найдите длину вектора АВ
1 способ
2
12+122+(-12)2 =
1)
2)
= 17
A(-35;-17;20) и B(-34;-5;8)
A(-35;-17;20)
B(-34; -5; 8)