Лекция 2. Формулы Бейеса, Бернулли.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формулы Бейеса, Бернулли презентация
Содержание
- 1. Формулы Бейеса, Бернулли
- 2. Вероятность гипотез. Формула Бейеса Следствием теоремы умножения
- 3. Вероятность гипотез. Формула Бейеса Два автомата производят
- 4. Вероятность гипотез. Формула Бейеса
- 5. Повторение испытаний. Формула Бернулли Если проводятся испытания,
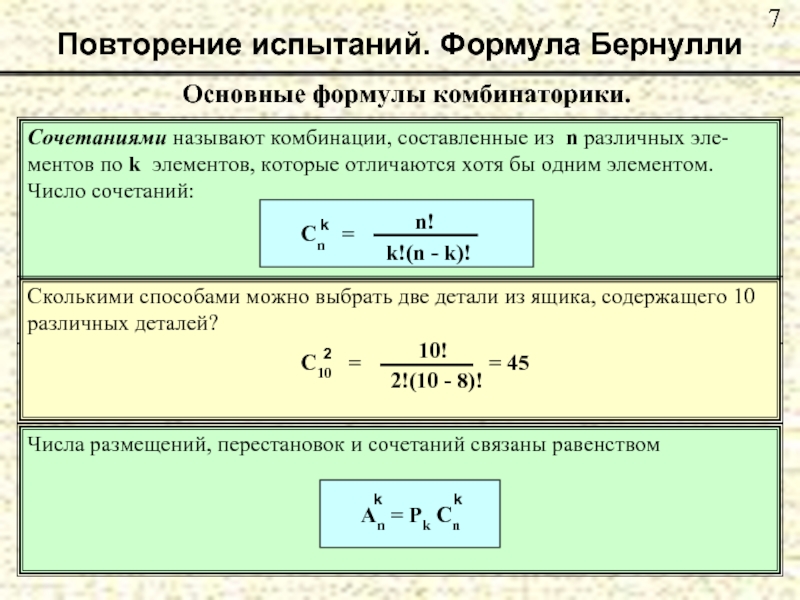
- 6. Повторение испытаний. Формула Бернулли Основные формулы комбинаторики.
- 7. Повторение испытаний. Формула Бернулли Основные формулы комбинаторики.
- 8. Повторение испытаний. Формула Бернулли
Вероятность гипотез. Формула Бейеса Следствием теоремы умножения и формулы полной вероятности является так называемая теорема гипотез, или формула Бейеса. Пусть событие А может наступить лишь при условии появления одного из
Слайд 1СТАТИСТИКА
Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
Введение в
теорию вероятности
Слайд 2Вероятность гипотез. Формула Бейеса
Следствием теоремы умножения и формулы полной вероятности
является так
называемая теорема гипотез, или формула Бейеса.
Пусть событие А может наступить лишь при условии появления
одного из несовместных событий (гипотез) В1, В2, …, Вn, кото-
рые образуют полную группу событий. Если событие А уже про-
изошло, то вероятности гипотез могут быть переоценены по
формуле Бейеса
Слайд 3Вероятность гипотез. Формула Бейеса
Два автомата производят одинаковые детали, которые поступают на
общий
конвейер. Производительность первого автомата вдвое больше производи-
тельности второго. Первый автомат производит в среднем 60% деталей отлич-
ного качества, а второй - 84%. Наудачу взятая с конвейера деталь оказалась
отличного качества. Найти вероятность того, что эта деталь произведена пер-
вым автоматом.
Событие А - деталь отличного качества. Гипотезы: В1 - деталь произведена
первым автоматом; B2 - деталь произведена вторым автоматом.
1) P(B1)=2/3; P(B2)=1/3.
2) P(А|В1)=0,6; P(А|В2)=0,84.
3) P(А) = P(B1)▪P(А|В1)+P(B2)▪P(А|В2)=2/3▪0,6+1/3▪0,84=0,68.
конвейер. Производительность первого автомата вдвое больше производи-
тельности второго. Первый автомат производит в среднем 60% деталей отлич-
ного качества, а второй - 84%. Наудачу взятая с конвейера деталь оказалась
отличного качества. Найти вероятность того, что эта деталь произведена пер-
вым автоматом.
Событие А - деталь отличного качества. Гипотезы: В1 - деталь произведена
первым автоматом; B2 - деталь произведена вторым автоматом.
1) P(B1)=2/3; P(B2)=1/3.
2) P(А|В1)=0,6; P(А|В2)=0,84.
3) P(А) = P(B1)▪P(А|В1)+P(B2)▪P(А|В2)=2/3▪0,6+1/3▪0,84=0,68.
4) P(B1 |А) = = = 10/17.
P(B1) ▪ P(А|В1)
P(А)
Слайд 5Повторение испытаний. Формула Бернулли
Если проводятся испытания, при которых вероятность появле-ния события
А в каждом испытании не зависит от исходов дру-гих испытаний, то такие испытания называют независимыми относительно события А.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0< p <1), событие наступит ровно k раз (безразлично в какой последова-тельности), равна
где q = 1 - p
