- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная сложной функции презентация
Содержание
- 1. Производная сложной функции
- 2. Производной функции f(x) в точке х0 называется
- 3. Физический смысл производной Касательной к кривой
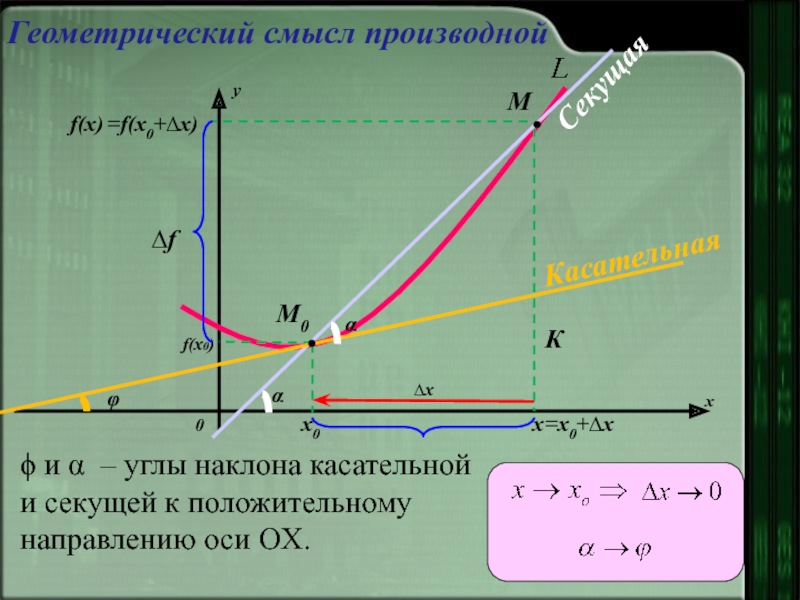
- 4. ϕ и α – углы наклона касательной
- 5. Геометрический смысл производной х у
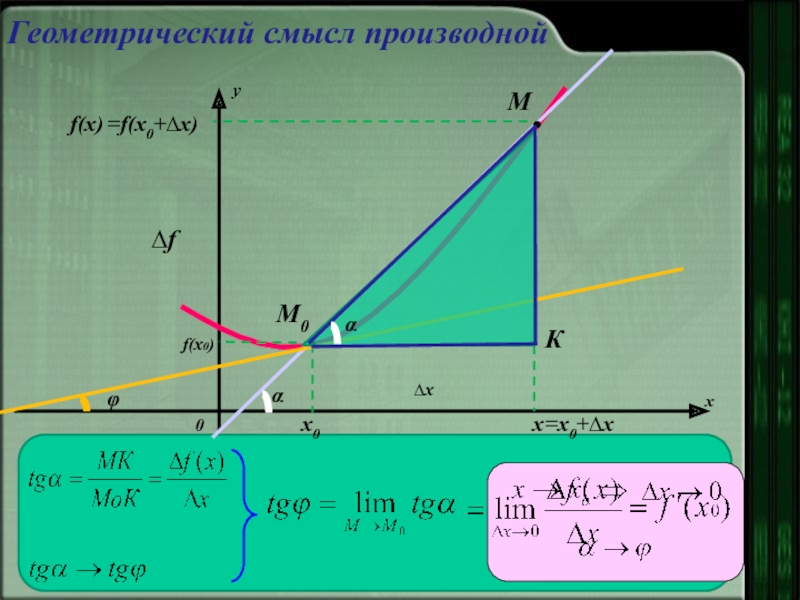
- 6. Геометрический смысл производной – это тангенс
- 7. Уравнение нормали Нормалью к графику
- 8. Составить уравнение касательной и нормали к графику
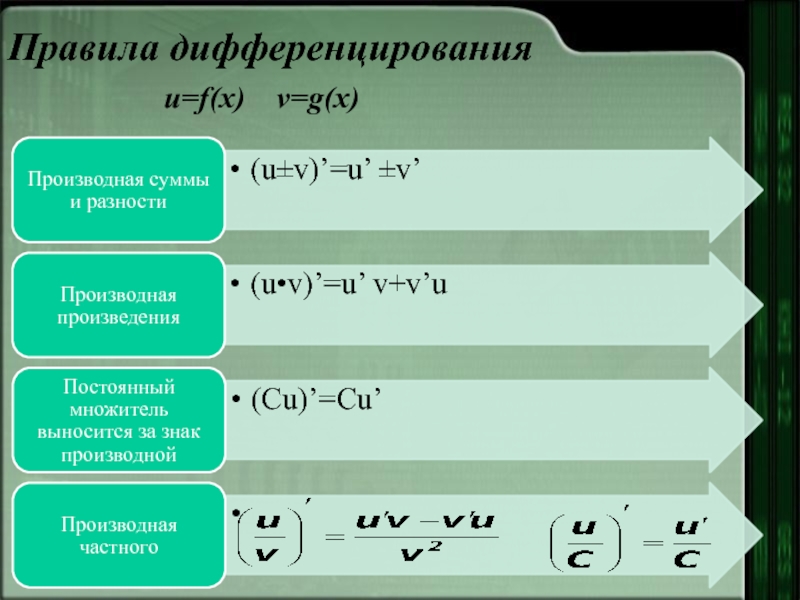
- 9. Правила дифференцирования u=f(x) v=g(x)
- 10. Производная сложной функции Функция является
- 11. Теорема о производной сложной функции:
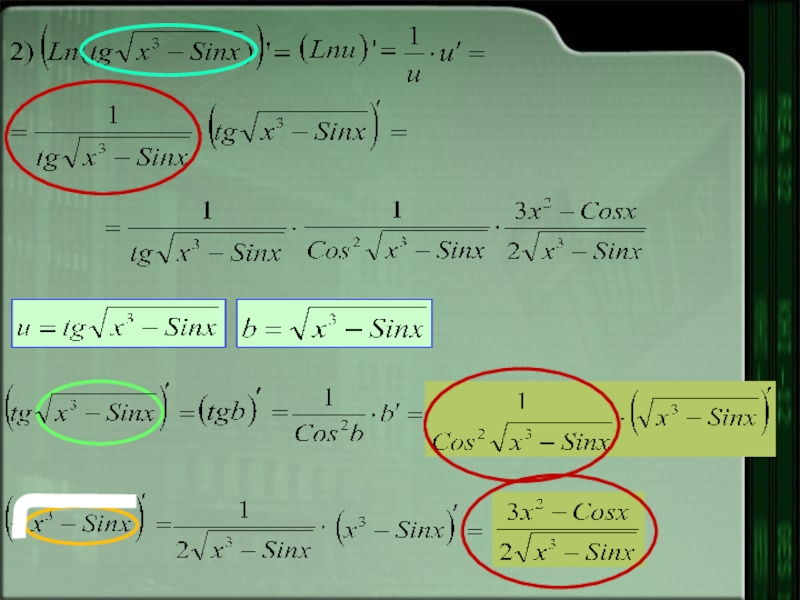
- 12. Примеры:
Слайд 2 Производной функции f(x) в точке х0 называется предел отношения приращения функции
Функцию, имеющую производную в точке х0 называют дифференцируемой в этой точке.
Слайд 3Физический смысл производной
Касательной к кривой L называется предельное положение секущей MM0,
Геометрический смысл производной
Слайд 4ϕ и α – углы наклона касательной и секущей к положительному
Геометрический смысл производной
х
у
0
М0
х0
f(x0)
М
х
f(x)
=x0+∆x
∆x
∆f
=f(x0+∆x)
α
φ
Секущая
Касательная
К
α
Слайд 6Геометрический смысл производной –
это тангенс угла наклона касательной, проведённой к
Уравнение касательной
Уравнение прямой, проходящей через точку х0
Слайд 7
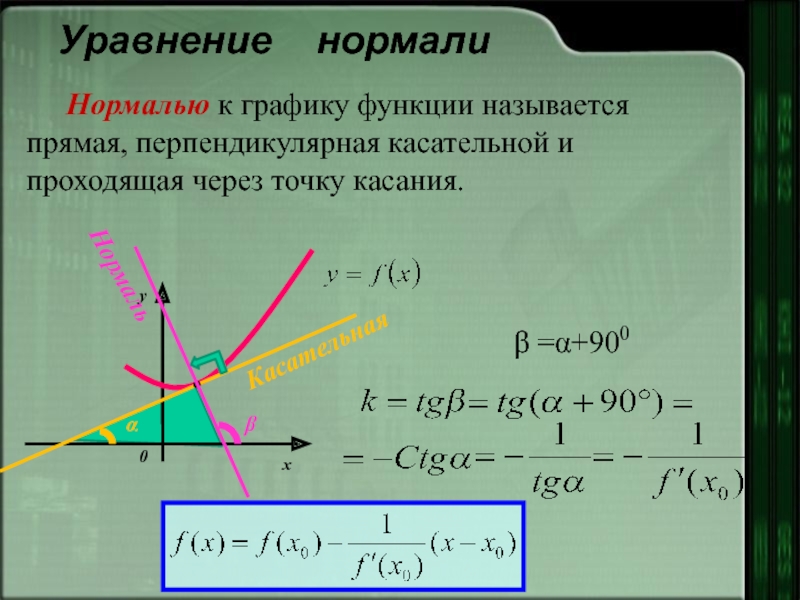
Уравнение нормали
Нормалью к графику функции называется прямая, перпендикулярная касательной и
х
у
0
α
Касательная
Нормаль
β
β =α+900
Слайд 8Составить уравнение касательной и нормали к графику функции y=2x3+x2-x+3 в точке
уравнение касательной
уравнение нормали
Слайд 10Производная сложной функции
Функция является сложной, если она зависит от
Определите является ли функция сложной:
да
нет
нет
да
да
да
нет
нет
да
Слайд 11
Теорема
о производной сложной функции:
Если функция Z(y(х)) дифференцируема