высшей математики БГУИР
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная функции в точке презентация
Содержание
- 1. Производная функции в точке
- 2. Производная функции в точке Пусть функция
- 3. Определение 2: Автор: И. В.
- 4. Односторонние производные функции в точке Правая
- 5. Пример 1: Найти производную функции Автор:
- 6. Теорема: Если функция f (x) имеет
- 7. Геометрический смысл производной функции в точке
- 8. Геометрический смысл производной функции в точке
- 9. Геометрический смысл производной функции в точке
- 10. Геометрический смысл производной функции в точке
- 11. Геометрический смысл производной функции в точке
- 12. Геометрический смысл производной функции в точке
- 13. Физический смысл производной функции в точке
- 14. Физический смысл производной функции в точке
- 15. Теорема 1: Основные формулы дифференцирования Пусть
- 16. Теорема 1: Основные формулы дифференцирования Автор:
- 17. Теорема 2: Дифференцирование сложной функции Пусть
- 18. Если функция f (x) имеет производную
- 19. 1. Постоянная функция f (x) =
- 20. 2. Показательная функция Автор: И.
- 21. 3. Степенная функция Автор: И.
- 22. 4. Логарифмическая функция Автор: И.
- 23. 5. Тригонометрические функции Автор: И.
- 24. 5. Тригонометрические функции Автор: И.
- 25. 5. Тригонометрические функции Автор: И.
- 26. 5. Тригонометрические функции Автор: И.
- 27. Высшая математика Автор: И.В.Дайняк, к.т.н., доцент кафедры высшей математики БГУИР math.mmts-it.org
Слайд 1ПРОИЗВОДНАЯ ФУНКЦИИ
В ТОЧКЕ
Лекция 1
Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры
Слайд 2
Производная функции в точке
Пусть функция f (x) определена в некоторой окрестности
точки х0.
Производной функции f (x) в точке x0 называется число, обозначаемое f ’(x0), равное пределу отношения
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
при
Дифференциальное исчисление
Определение 1:
если этот предел существует.
Слайд 3
Определение 2:
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производную
функции y = f (x) принято обозначать так:
Дифференциальное исчисление
Производная функции в точке
Обозначения:
Производная функции f (x) в точке x0 есть предел отношения
её приращения
к соответствующему приращению
её аргумента
при
Слайд 4
Односторонние производные функции в точке
Правая производная:
Если функция f (x) определена в
некоторой правой полуокрестности точки x0 , то её правой производной называется предел
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Левая производная:
Если функция f (x) определена в некоторой левой полуокрестности точки x0 , то её левой производной называется предел
Слайд 5
Пример 1:
Найти производную функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей
математики БГУИР
в точке х0 = 0.
Дифференциальное исчисление
Производная функции в точке
Пример 2:
Найти производную функции
в точках х1 = 0 и х2 = 1.
Слайд 6
Теорема:
Если функция f (x) имеет производную в точке x0, то она
непрерывна в точке x0.
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Обратное утверждение неверно.
Дифференциальное исчисление
Производная функции в точке
Слайд 7
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
Пусть f (x) – непрерывная функция, определённая в некоторой окрестности точки x0.
Дифференциальное исчисление
Рассмотрим две точки:
Слайд 8
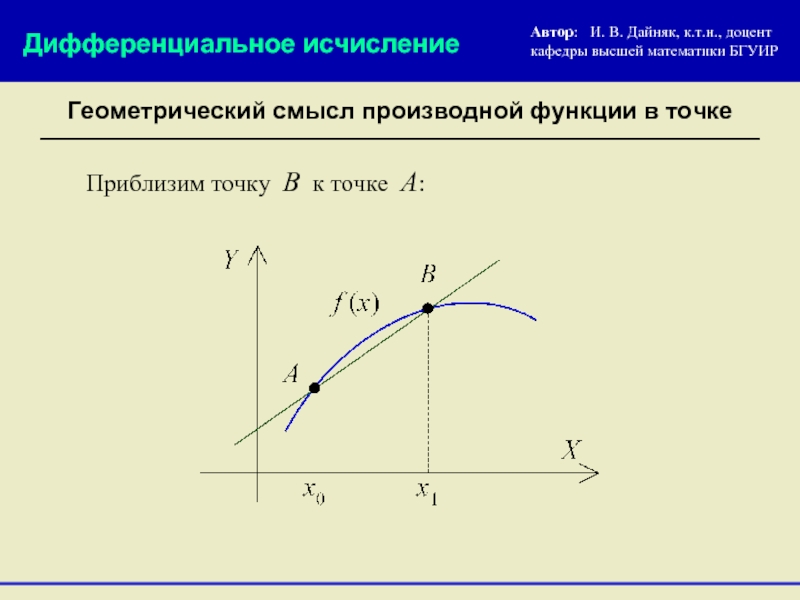
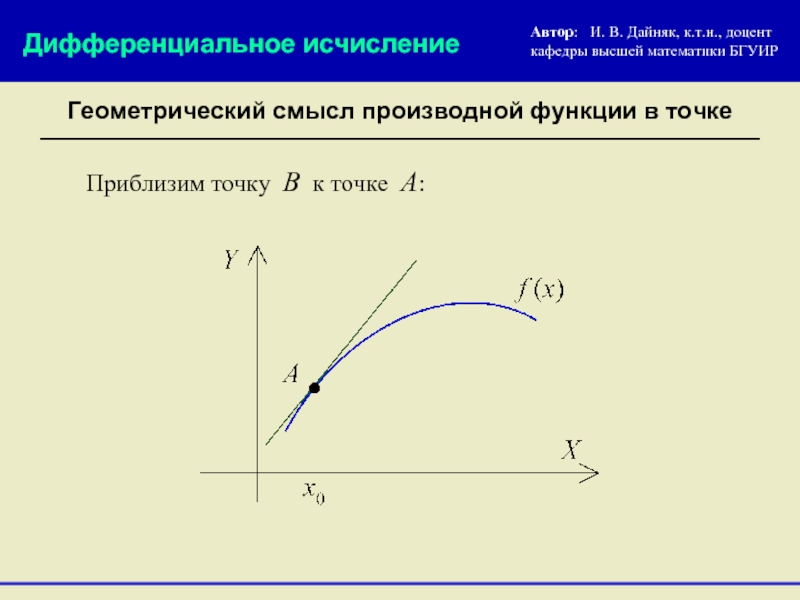
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Слайд 9
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Слайд 10
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Слайд 11
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Слайд 12
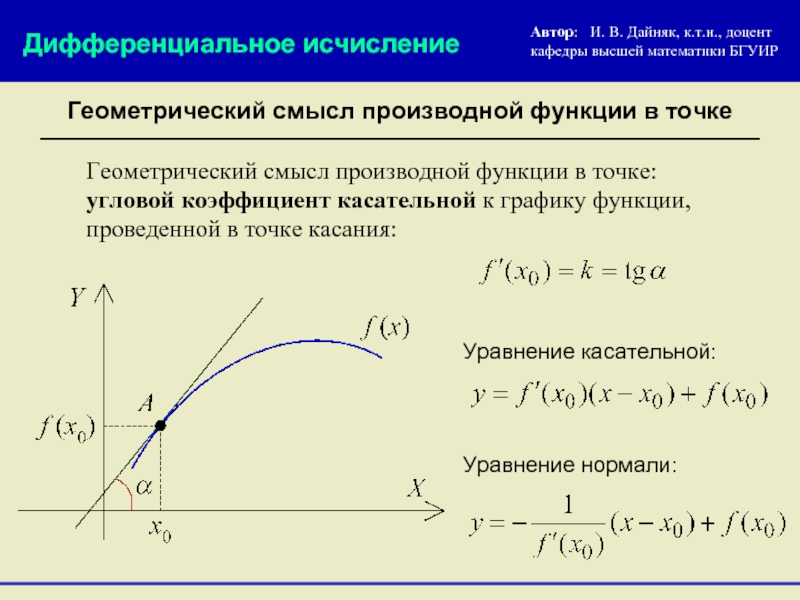
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
Геометрический смысл производной функции в точке: угловой коэффициент касательной к графику функции, проведенной в точке касания:
Дифференциальное исчисление
Уравнение касательной:
Уравнение нормали:
Слайд 13
Физический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
1. Пусть материальная точка М движется прямолинейно,
и функция s(t) есть пройденный ею путь за время t.
Дифференциальное исчисление
Пусть t0 – момент начала движения.
Тогда отношение
– средняя скорость движения.
Предел
– мгновенная скорость
точки в момент t0.
Слайд 14
Физический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Пусть Δt – промежуток времени.
Тогда
– средняя сила тока за время Δt.
Предел
– мгновенный ток.
2. Пусть q (t0) – количество электричества, протекающего через
поперечное сечение проводника в момент времени t0.
Отношение
Слайд 15
Теорема 1: Основные формулы дифференцирования
Пусть функции u = u(x) и v
= v(x) имеют производную
в точке x = x0. Тогда функции
в точке x = x0. Тогда функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
тоже имеют производные в точке x = x0, вычисляемые по формулам:
Дифференциальное исчисление
Производная функции в точке
1)
константу можно выносить за знак производной
Слайд 16
Теорема 1: Основные формулы дифференцирования
Автор: И. В. Дайняк, к.т.н., доцент
кафедры
высшей математики БГУИР
Дифференциальное исчисление
Производная функции в точке
2) формула производной суммы
3) формула производной произведения
4) формула производной частного
Слайд 17
Теорема 2: Дифференцирование сложной функции
Пусть функция g(x) имеет производную в точке
x0, а функция f (y) имеет производную в точке y0 = g(x0). Тогда сложная функция f (g(x)) имеет производную в точке x0, вычисляемую по формуле
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
или
Дифференциальное исчисление
Производная функции в точке
Слайд 18
Если функция f (x) имеет производную в любой точке некоторого интервала
[a, b], то её производная на этом интервале может быть выражена в виде некоторой функции g(x) = f ’(x), которая находится по основным формулам дифференцирования (теорема 1) и правилу нахождения производной сложной функции (теорема 2).
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производная функции на отрезке
Слайд 19
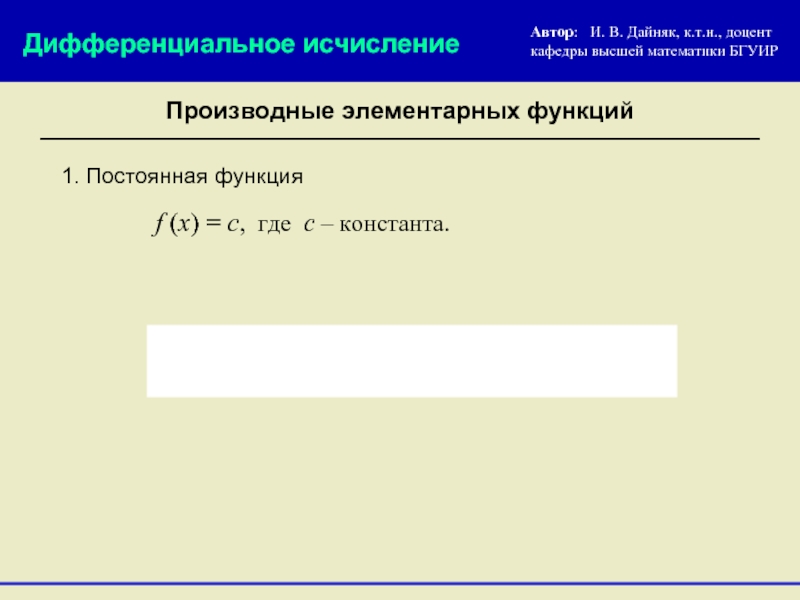
1. Постоянная функция
f (x) = c, где с – константа.
Автор:
И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
Слайд 20
2. Показательная функция
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
БГУИР
Дифференциальное исчисление
Производные элементарных функций
Отсюда заключаем:
Слайд 21
3. Степенная функция
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
БГУИР
Дифференциальное исчисление
Производные элементарных функций
При
имеем:
Слайд 22
4. Логарифмическая функция
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
БГУИР
Дифференциальное исчисление
Производные элементарных функций
Отсюда следует, что
Кроме того,
Слайд 23
5. Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
БГУИР
Дифференциальное исчисление
Производные элементарных функций
Синус: sin x
Слайд 24
5. Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
БГУИР
Дифференциальное исчисление
Производные элементарных функций
Косинус: cos x
Слайд 25
5. Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
БГУИР
Дифференциальное исчисление
Производные элементарных функций
Тангенс:
Производная находится по формуле производной частного:
Слайд 26
5. Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
БГУИР
Дифференциальное исчисление
Производные элементарных функций
Тангенс:
Производная находится по формуле производной частного:
Слайд 27
Высшая математика
Автор: И.В.Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
math.mmts-it.org
