- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная функции презентация
Содержание
- 1. Производная функции
- 2. Пусть функция y=f(x) определена в точках x
- 3. Задача о мгновенной скоростии прямолинейного движения Пусть
- 4. Задача о проведении касательной к графику функции
- 5. Задача о проведении касательной к графику функции
- 6. Производной функции y=f(x) в точке x0
- 7. Механический смысл производной Из и используя определение
- 8. Геометрический смысл производной Из и используя определение
- 9. Домашнее задание Подготовить таблицу производных основных элементарных функций
- 10. Общие правила дифференцирования
- 11. Дифференцирование сложных функций Правило: Производная сложной функции
Пусть функция y=f(x) определена в точках x и x0. Разность (x - x0) называют приращением аргумента и обозначают Δx; Разность f(x)-f(x0) называют приращением функции и обозначают Δy или Δf.
Слайд 2Пусть функция y=f(x) определена в точках x и x0.
Разность (x
- x0) называют приращением аргумента и обозначают Δx;
Разность f(x)-f(x0) называют приращением функции и обозначают Δy или Δf.
Δx= x - x0 => x=x0+ Δx,
Δf= f(x)-f(x0) => Δf= f(x0+ Δx) -f(x0).
Разность f(x)-f(x0) называют приращением функции и обозначают Δy или Δf.
Δx= x - x0 => x=x0+ Δx,
Δf= f(x)-f(x0) => Δf= f(x0+ Δx) -f(x0).
Производная функции
Слайд 3Задача о мгновенной скоростии прямолинейного движения
Пусть по прямой движется точка по
закону S=S(t) [S(t) – положение точки на прямойв момент времени t].
0
M
S
Средняя скорость за промежуток времени от до :
Полагая
Мгновенной скоростью в момент времени t называют предел средней скорости движения за промежуток времени при Δt→0.
1
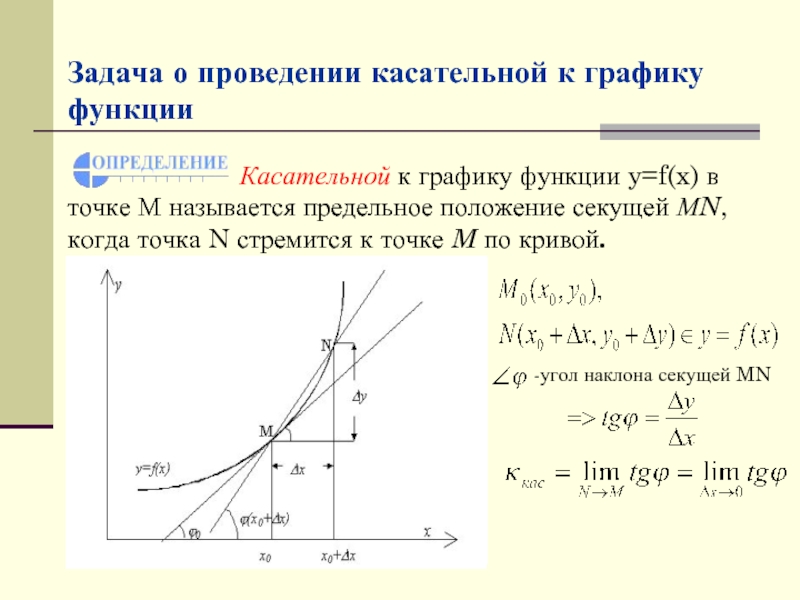
Слайд 4Задача о проведении касательной к графику функции
Касательной к графику функции y=f(x) в точке М называется предельное положение секущей МN, когда точка N стремится к точке M по кривой.
-угол наклона секущей MN
Слайд 5Задача о проведении касательной к графику функции
-угол наклона касательной к оси ОХ.
Так как,
Мы определили угловой коэффициент касательной, как приращение ординаты к приращению абсциссы, когда последнее стремится к 0.
2
Слайд 6 Производной функции y=f(x) в точке x0 называется предел отношения приращения
функции в этой точке к приращению аргумента при Δx →0 (если этот предел существует).
Обозначается: (Лагранж), (Лейбниц)
Обозначается: (Лагранж), (Лейбниц)
Слайд 7Механический смысл производной
Из
и используя определение производной,
можем записать:
Таким образом, производная от
пути по времени есть мгновенная скорость.
Слайд 8Геометрический смысл производной
Из
и используя определение производной,
можем записать:
Таким образом, производная от
ординаты кривой по абсциссе есть угловой коэффициент касательной к этой кривой.
Слайд 11Дифференцирование сложных функций
Правило: Производная сложной функции по основному аргументу равна произведению
производной этой функции по промежуточному аргументу на производную промежуточного аргумента по основному.
