- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика. Теория вероятностей презентация
Содержание
- 1. Математика. Теория вероятностей
- 2. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ. СЛУЧАЙНЫЕ
- 3. СЛУЧАЙНОЕ СОБЫТИЕ ДОСТОВЕРНОЕ НЕВОЗМОЖНОЕ СЛУЧАЙНОЕ – событие,
- 4. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ. СЛУЧАЙНЫЕ
- 5. ВЕРОЯТНОСТЬ ВЕРОЯТНОСТЬ – количественная характеристика степени возможности
- 6. m = n 0 < m <
- 7. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ НЕСОВМЕСТНЫЕ СОБЫТИЯ (А) –
- 8. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ События называют НЕЗАВИСИМЫМИ, если
- 9. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ. СЛУЧАЙНЫЕ
- 10. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ СЛУЧАЙНАЯ ВЕЛИЧИНА (СВ) – величина,
- 11. Распределение ДСВ представляет собой совокупность ее возможных
- 12. Величины, которые описывают случайную величину, называют ЧИСЛОВЫМИ
- 13. Математическое ожидание примерно равно (тем точнее, чем
- 14. случайной величины характеризует разброс случайных величин в
- 15. Плотность вероятности показывает, как изменяется вероятность, отнесенная
- 16. b Функция распределения НСВ
- 18. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ. СЛУЧАЙНЫЕ
- 19. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ЗАКОН РАСПРЕДЕЛЕНИЯ – связь между
- 20. ОСОБЕННОСТИ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ 1. Распределение является
- 21. x a x a x f(x) a+σ
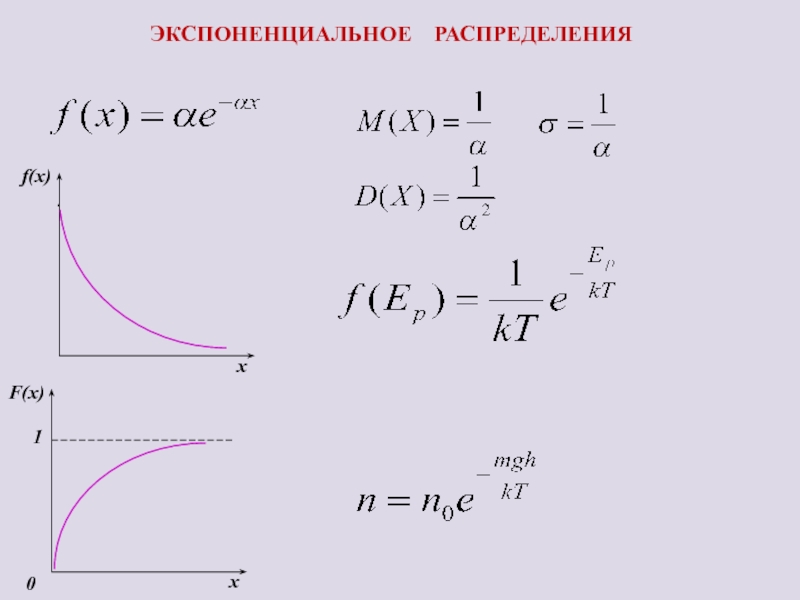
- 22. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЯ
- 23. Тема 2. "МАТЕМАТИЧЕСКАЯ СТАТИСТИКА" ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ
- 24. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ –
- 25. ВЫБОРОЧНАЯ СОВОКУПНОСТЬ ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
- 26. ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ МОДА (Мо) МЕДИАНА (Ме)
- 27. ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ – среднее арифметическое квадратов отклонения вариант от их среднего значения.
- 28. ··· ··· ··· НЕПРЕРЫВНОЕ СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ или
Слайд 2СЛУЧАЙНЫЕ СОБЫТИЯ.
ВЕРОЯТНОСТЬ.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕГО ХАРАКТЕРИСТИКИ.
ЗАКОНЫ
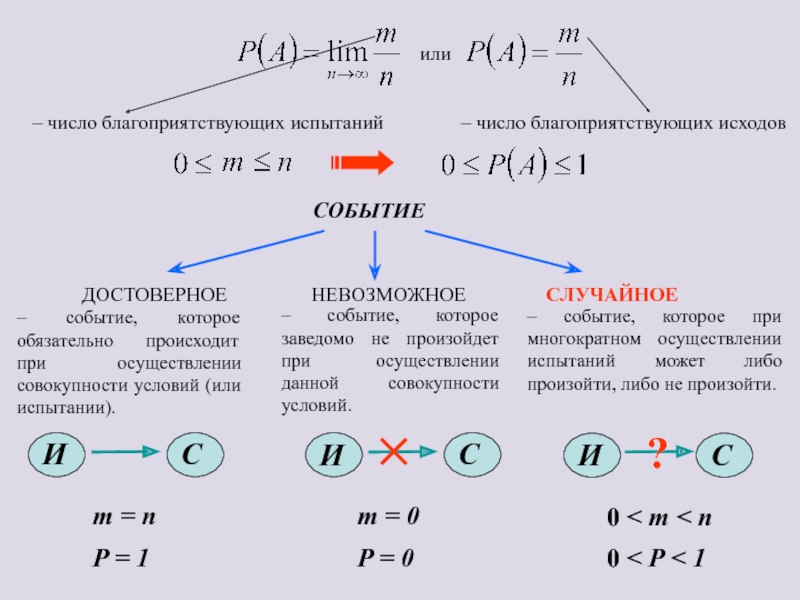
Слайд 3СЛУЧАЙНОЕ СОБЫТИЕ
ДОСТОВЕРНОЕ
НЕВОЗМОЖНОЕ
СЛУЧАЙНОЕ
– событие, которое обязательно происходит при осуществлении совокупности условий (или
– событие, которое заведомо не произойдет при осуществлении данной совокупности условий.
– событие, которое при многократном осуществлении испытаний может либо произойти, либо не произойти.
СОБЫТИЕ (ЯВЛЕНИЕ)
Слайд 4СЛУЧАЙНЫЕ СОБЫТИЯ.
ВЕРОЯТНОСТЬ.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕГО ХАРАКТЕРИСТИКИ.
ЗАКОНЫ
Слайд 5ВЕРОЯТНОСТЬ
ВЕРОЯТНОСТЬ – количественная характеристика степени возможности наступления события.
n
– число испытаний
m
–
относительная частота события А
Вероятность равна отношению числа благоприятствующих исходов (m) к общему числу исходов (n)
Слайд 6m = n
0 < m < n
m = 0
P = 1
P
0 < P < 1
– число благоприятствующих испытаний
– число благоприятствующих исходов
Слайд 7ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
НЕСОВМЕСТНЫЕ СОБЫТИЯ (А) – события, которые ни при каких
ПРОТОВОПОЛОЖНЫЕ СОБЫТИЯ ( ) – события, появление одного из которых исключает появление другого (появление четной и нечетной цифры на верхней грани игральной кости)
Вероятность появления одного из нескольких несовместных событий равна сумме их вероятностей.
сумма вероятностей событий, образующих полную систему равна 1.
Систему событий называют полной, если при любом испытании наступит одно из событий этой системы (выпадение цифр от 1 до 6 на верхней грани игральной кости)
УСЛОВИЕ НОРМИРОВКИ:
Слайд 8ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
События называют НЕЗАВИСИМЫМИ, если наступление одного не зависит от
Вероятность такого события меньше вероятности каждого отдельного события
Слайд 9СЛУЧАЙНЫЕ СОБЫТИЯ.
ВЕРОЯТНОСТЬ.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕГО ХАРАКТЕРИСТИКИ.
ЗАКОНЫ
Слайд 10СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
СЛУЧАЙНАЯ ВЕЛИЧИНА (СВ) – величина, значение которой зависит от стечения
X, Y, Z – обозначение случайной величины,
x, y, z – значения случайной величины.
СВ, которая принимает отдельные, изолированные значения (или счетное множество значений).
ДИСКРЕТНАЯ (ДСВ)
СВ, которая может принимать все значения из некоторого промежутка.
НЕПРЕРЫВНАЯ (НСВ)
число родившихся мальчиков среди ста новорожденных;
расстояние, которое пролетит снаряд при выстреле из орудия;
размер эритроцита;
число заболевших гриппом;
частота пульса пациента;
температура тела.
Слайд 11Распределение ДСВ представляет собой совокупность ее возможных значений и соответствующих им
(x1 , p1)
(x2 , p2)
(x3 , p3)
(x4 , p4)
МНОГОУГОЛЬНИК РАСПРЕДЕЛЕНИЯ
УСЛОВИЕ НОРМИРОВКИ
ДИСКРЕТНАЯ СВ принимает отдельные, изолированные значения (или счетное множество значений).
Слайд 12Величины, которые описывают случайную величину, называют ЧИСЛОВЫМИ ХАРАКТЕРИСТИКАМИ случайной величины.
случайной величины
Слайд 13Математическое ожидание примерно равно (тем точнее, чем больше число испытаний) среднему
xmin
xmax
M(X)
Математическое ожидание характеризует расположение распределения.
Слайд 14случайной величины характеризует разброс случайных величин в данном распределении.
Истинной мерой разброса случайной величины в данном распределении является
Слайд 15Плотность вероятности показывает, как изменяется вероятность, отнесенная к интервалу НСВ в
Вероятность того, что СВ принимает какое-либо значение в интервале (a; b):
УСЛОВИЕ НОРМИРОВКИ:
Распределение НСВ задают функцией распределения вероятностей и функцией распределения непрерывной случайной величины.
НЕПРЕРЫВНАЯ СВ может принимать все значения из некоторого промежутка.
Слайд 16b
Функция распределения НСВ
a
X
x’
0 < F(x) < 1
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
ДИСПЕРСИЯ
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
Слайд 18СЛУЧАЙНЫЕ СОБЫТИЯ.
ВЕРОЯТНОСТЬ.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕГО ХАРАКТЕРИСТИКИ.
ЗАКОНЫ
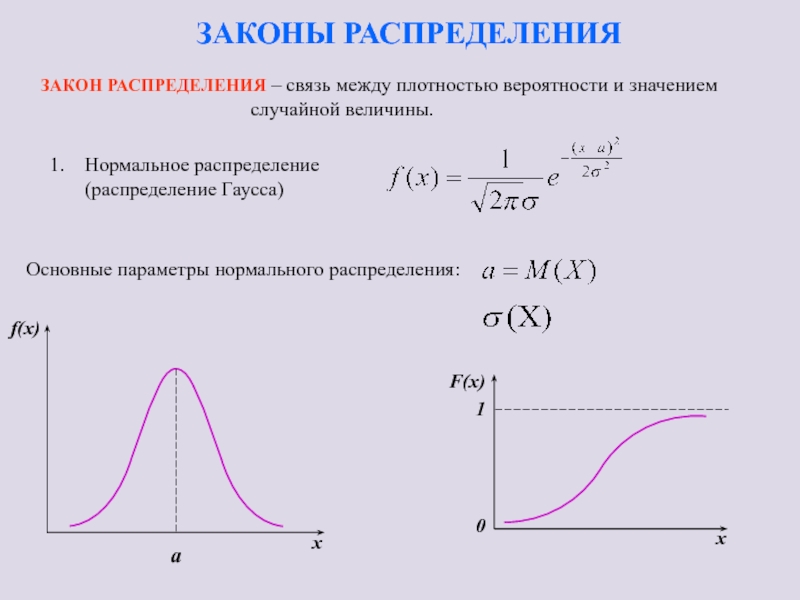
Слайд 19ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
ЗАКОН РАСПРЕДЕЛЕНИЯ – связь между плотностью вероятности и значением
1
Основные параметры нормального распределения:
Нормальное распределение
(распределение Гаусса)
a
Слайд 20ОСОБЕННОСТИ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ
1. Распределение является симметричным относительно перпендикуляра, проходящего через
2. При изменении математического ожидания график нормального
распределения смещается относительно оси абсцисс
3. Изменение среднего квадратического
отклонения влияет на форму «крыльев»
распределения. Чем шире размах «крыльев»
(больше разброс значений), тем шире размах
«крыльев».
4. Площадь под кривой нормального распределения нормирована на 1, т.е. достоверно
найти случайную величину в диапазоне значений
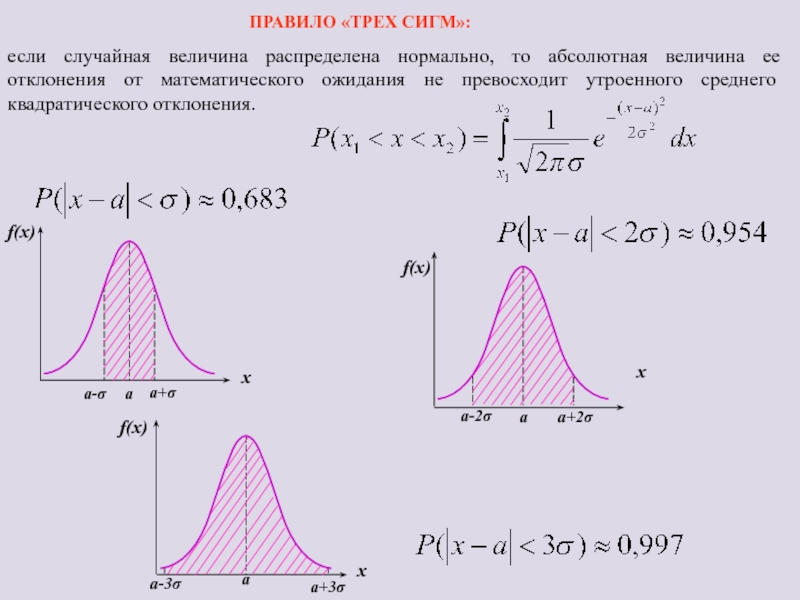
Слайд 21x
a
x
a
x
f(x)
a+σ
a-σ
a+2σ
a-2σ
a+3σ
a-3σ
ПРАВИЛО «ТРЕХ СИГМ»:
если случайная величина распределена нормально, то абсолютная величина ее
Слайд 23Тема 2. "МАТЕМАТИЧЕСКАЯ СТАТИСТИКА"
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА – наука о
ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ:
анализ статистических данных;
определение вида распределения, которому соответствуют данные;
составление прогнозов и проверка гипотез.
Слайд 24ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ – большая статистическая совокупность однородных элементов
ВЫБОРОЧНАЯ СОВОКУПНОСТЬ (ВЫБОРКА) – часть генеральной совокупности, объекты отобранные для исследования.
представительная (репрезентативная);
случайная;
достаточный объем.
большая,
n > 30
малая,
n ≤ 30
не всегда доступны для исследования все объекты;
подвижные совокупности;
возможно потребуется уничтожение всех объектов при исследовании;
большие временные и материальные затраты.
Слайд 25
ВЫБОРОЧНАЯ СОВОКУПНОСТЬ
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
x1, x2, … и xk – ВАРИАНТЫ;
Сумма всех
ОТНОСИТЕЛЬНАЯ ЧАСТОТА – отношение частоты к объему выборки.
РАНЖИРОВАННЫЙ СТАТИСТИЧЕСКИЙ РЯД – совокупность всех значений в выборке, расположенных в определенном порядке.
ДИСКРЕТНОЕ СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ или ВАРИАЦИОННЫЙ РЯД – совокупность всех вариант и соответствующих им частот или относительных частот.
p*
n1, n2, … и nk – ЧАСТОТЫ.
ПОЛИГОН ЧАСТОТ
Слайд 26ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
МОДА (Мо)
МЕДИАНА (Ме)
– варианта, которой соответствует набольшая частота.
– варианта,
, если n – нечетное число;
, если n – четное число.
– среднее арифметическое значение вариант статистического распределения.
Слайд 27ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
– среднее арифметическое квадратов отклонения вариант от их среднего
Слайд 28···
···
···
НЕПРЕРЫВНОЕ СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ или ИНТЕРВАЛЬНЫЙ РЯД –
xmin
xmax
совокупность интервалов, в которых
ГИСТОГРАММА
– совокупность смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине интервала, а высоты равны отношение частоты или относительной частоты к ширине интервала.