- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная функции презентация
Содержание
- 1. Производная функции
- 2. Производная Производная функции это отношение приращения функции
- 3. Вычисление производных
- 4.
- 5. Правило дифференцирования (нахождение производной)
- 6.
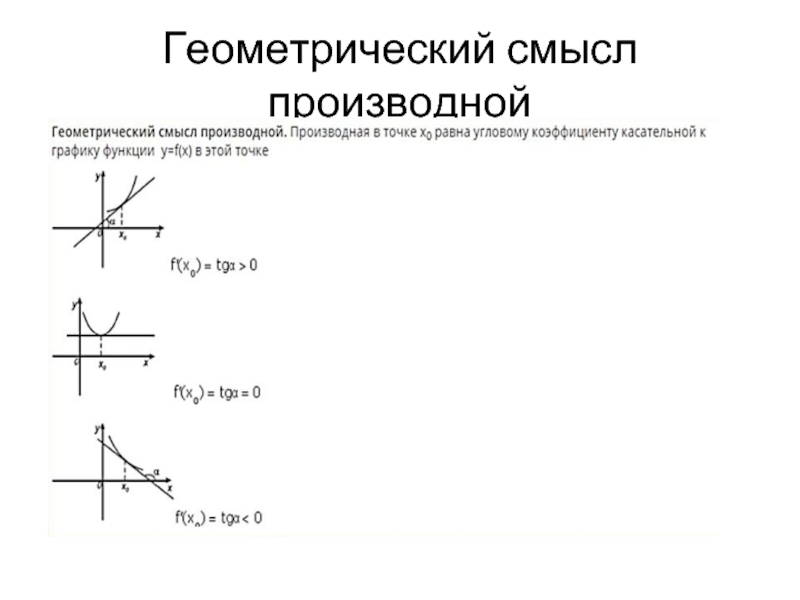
- 7. Физический смысл производной
- 8. Примеры заданий
- 9. 20 59 8
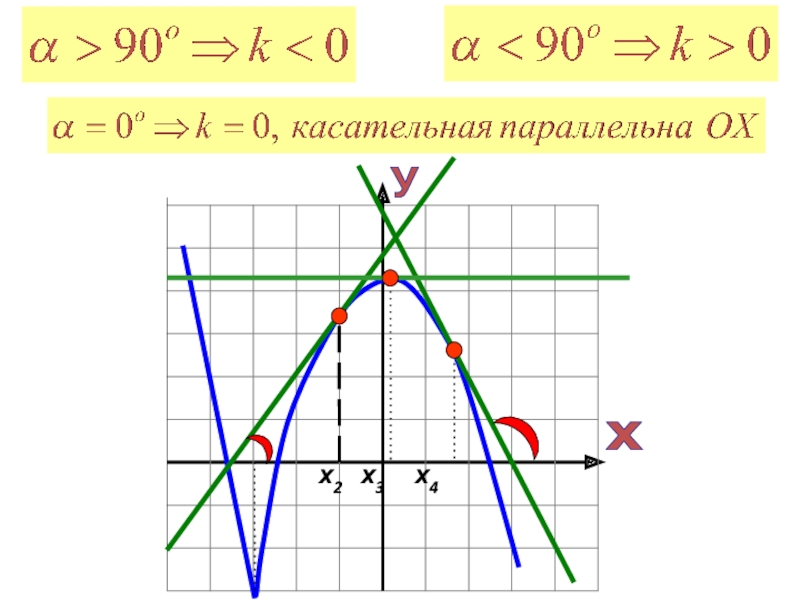
- 10. Геометрический смысл производной
- 12. Уравнение касательной
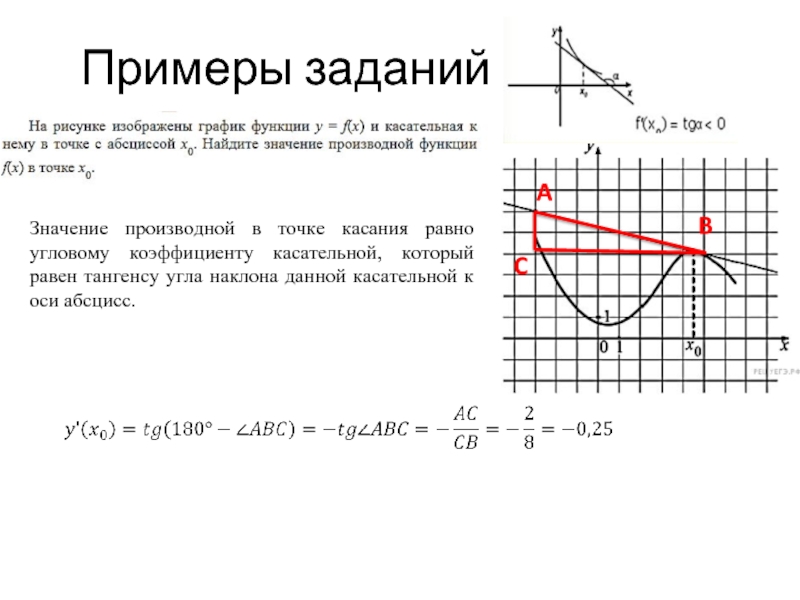
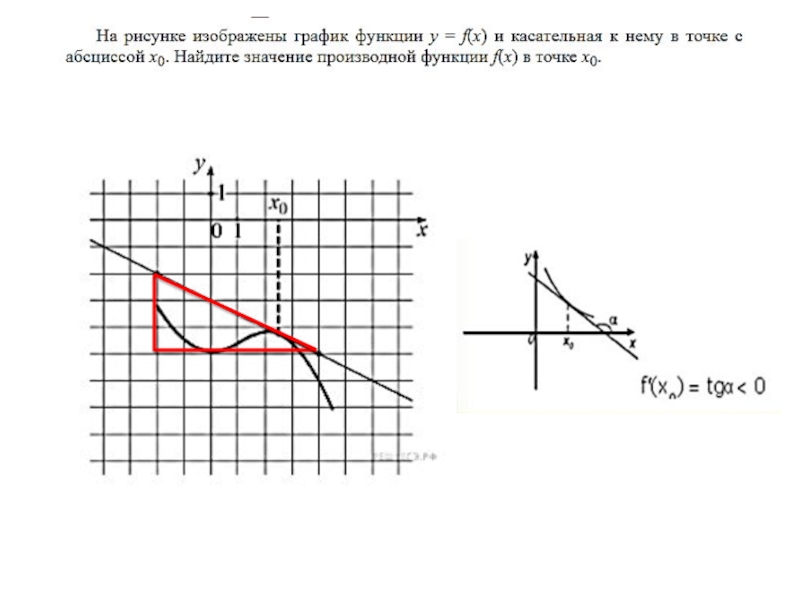
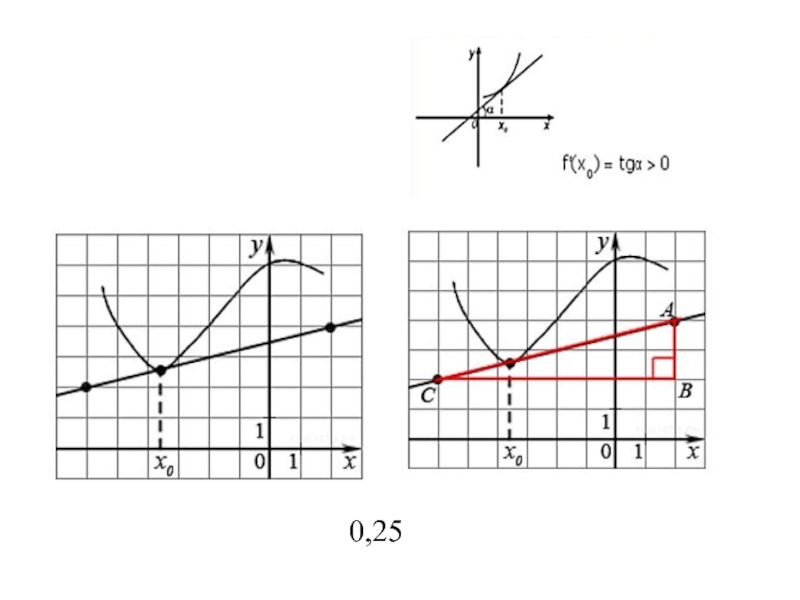
- 13. Примеры заданий Значение производной в точке касания
- 15. 0,25
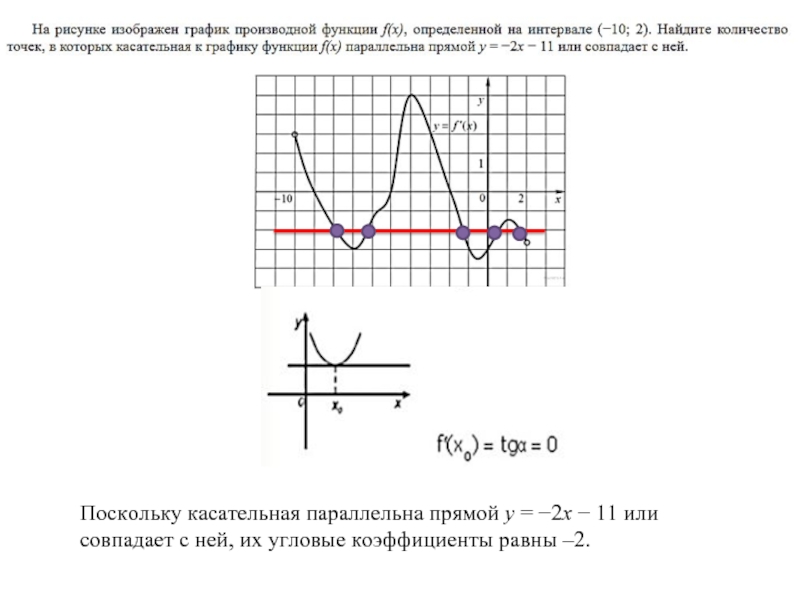
- 16. Примеры заданий Поскольку касательная параллельна прямой y = −2x − 11 или
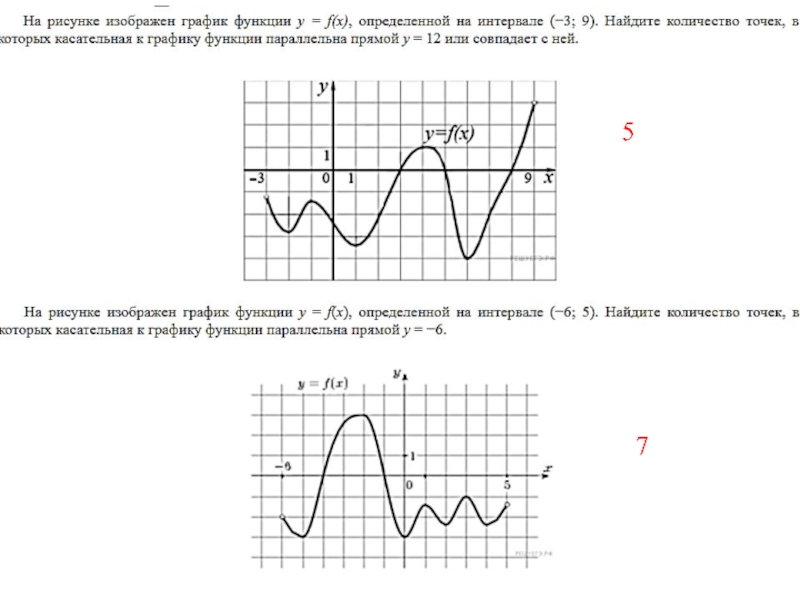
- 18. 5 7
- 19. 5
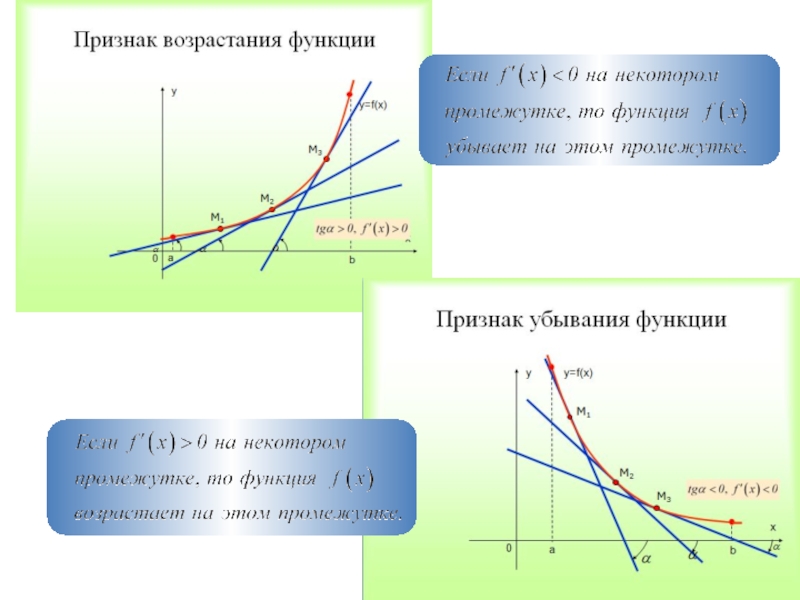
- 21. Применение производной к исследованию функции
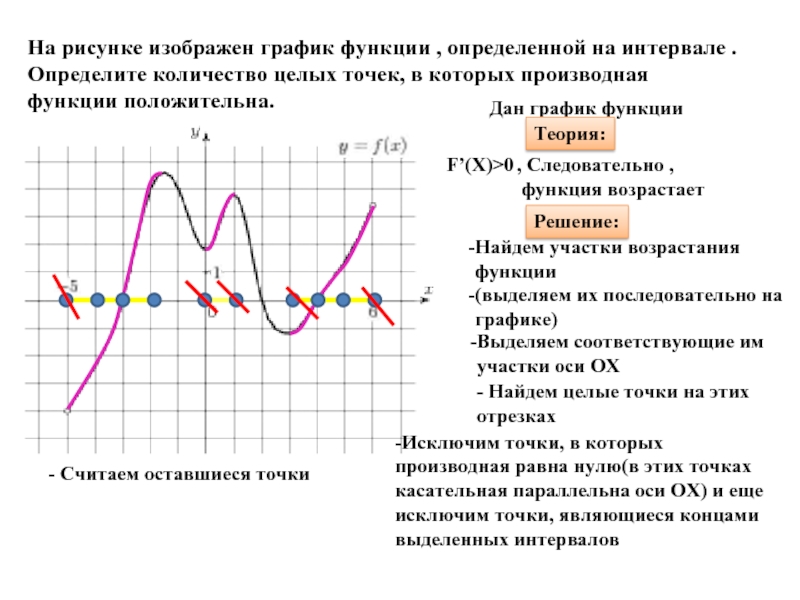
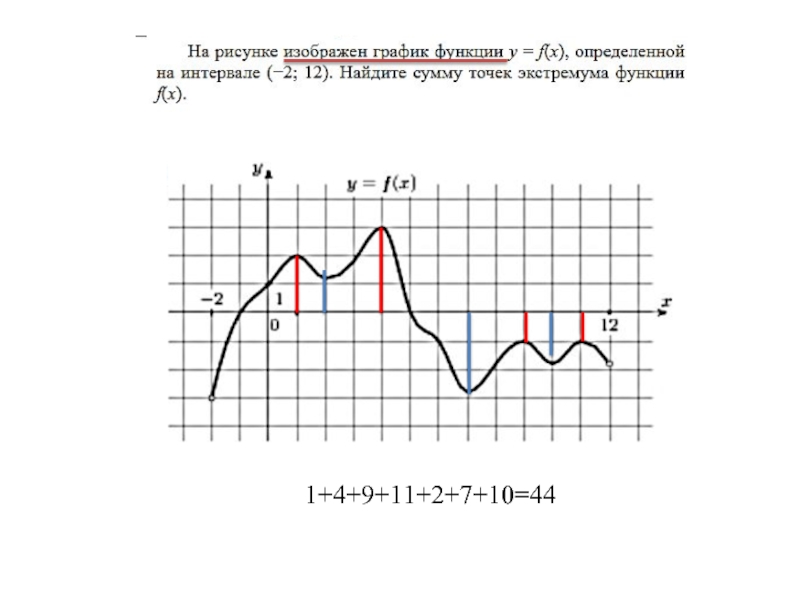
- 23. На рисунке изображен график функции ,
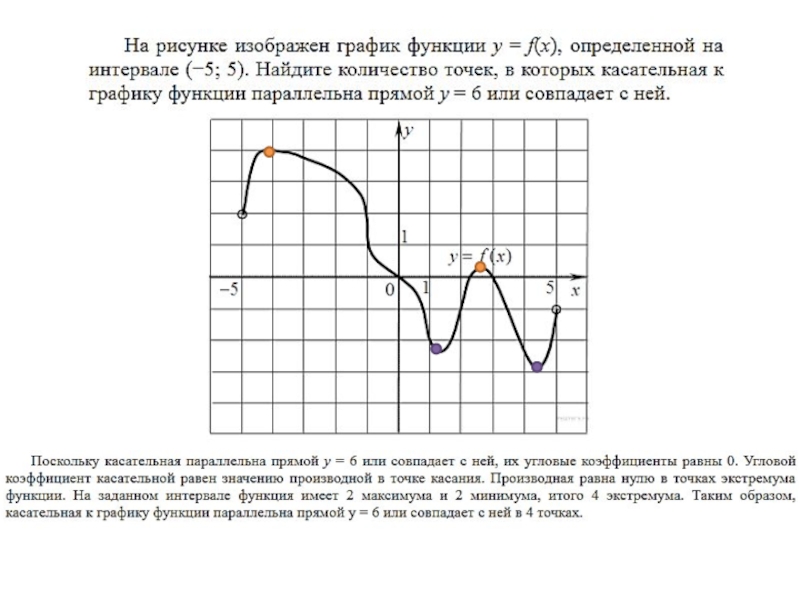
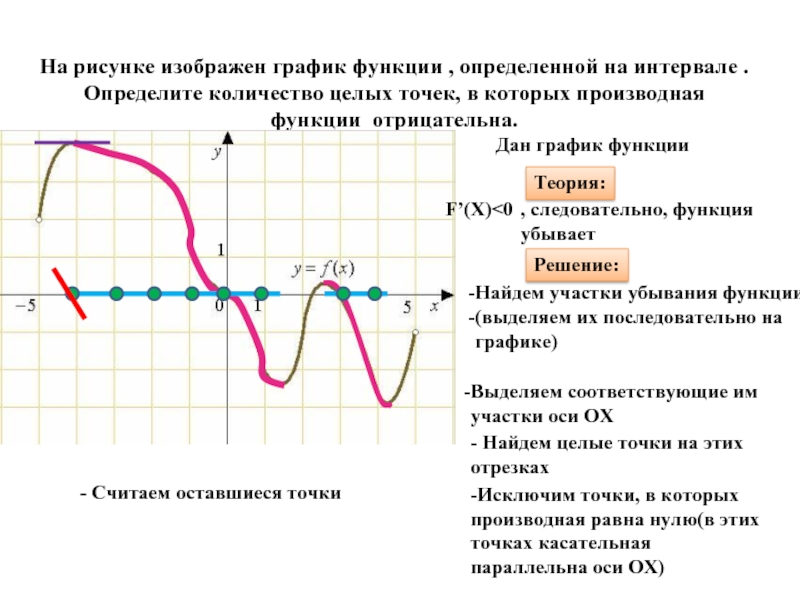
- 24. На рисунке изображен график функции , определенной
- 25. 1+4+9+11+2+7+10=44
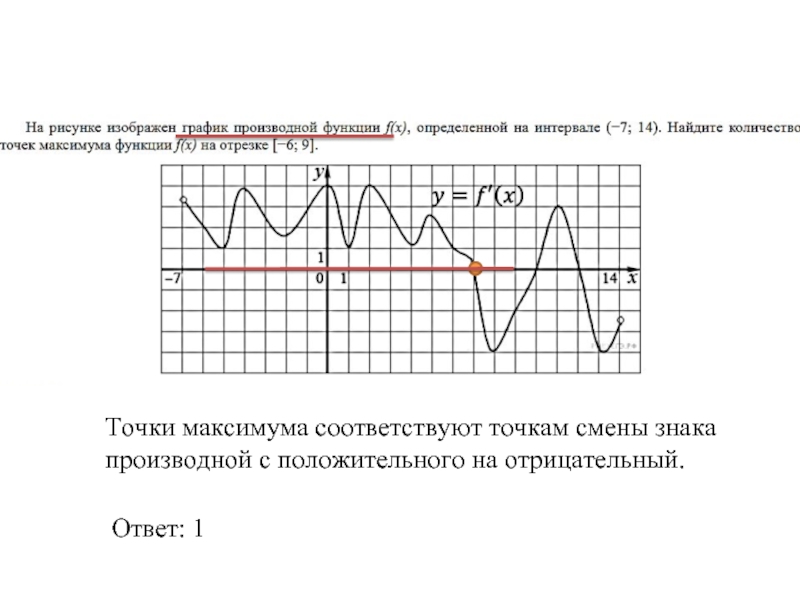
- 26. Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. Ответ: 1
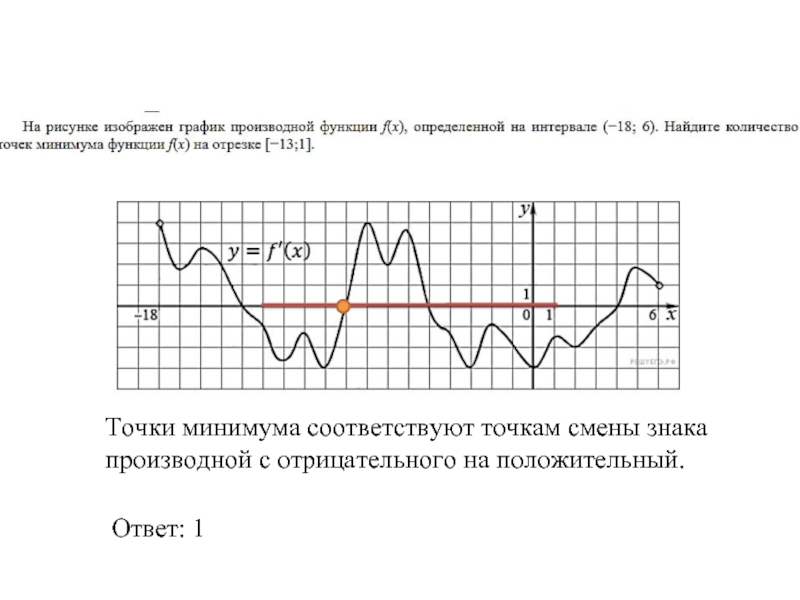
- 27. Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. Ответ: 1
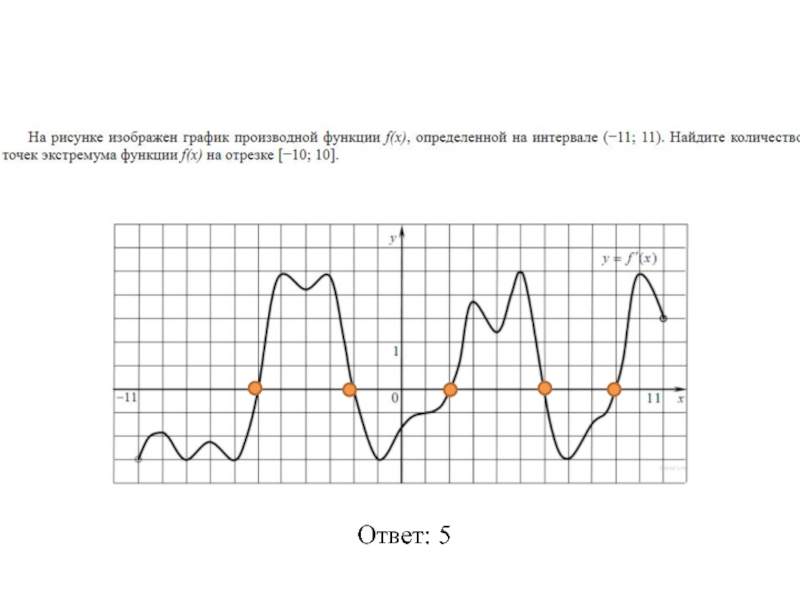
- 28. Ответ: 5
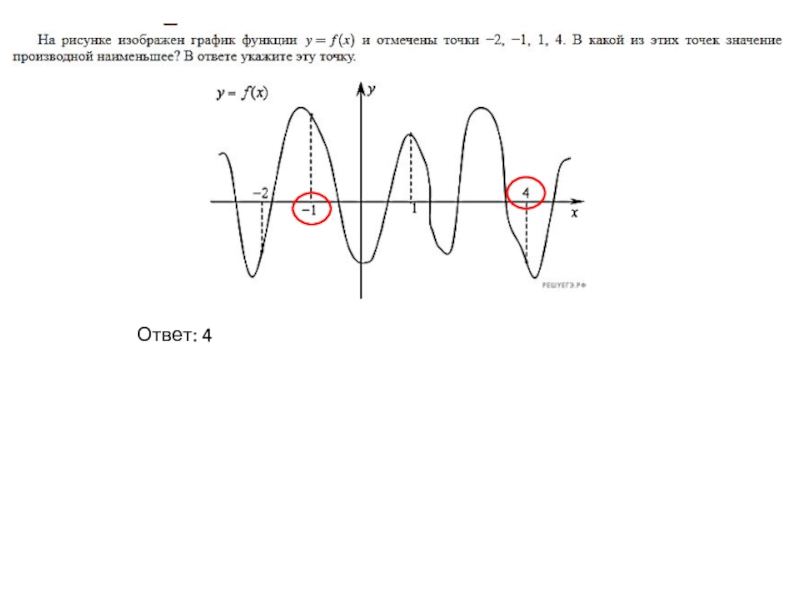
- 29. Ответ: 4
Слайд 2Производная
Производная функции это отношение приращения функции к приращению аргумента при бесконечно
Приращением в математике называют изменение. То, насколько изменился аргумент (x) при продвижении вдоль оси, называется приращением аргумента и обозначается Δx. То, насколько изменилась функция (высота) при продвижении вперед вдоль оси Ox, на расстояние Δx, называется приращением функции и обозначается Δf.
Слайд 13Примеры заданий
Значение производной в точке касания равно угловому коэффициенту касательной, который
A
B
C
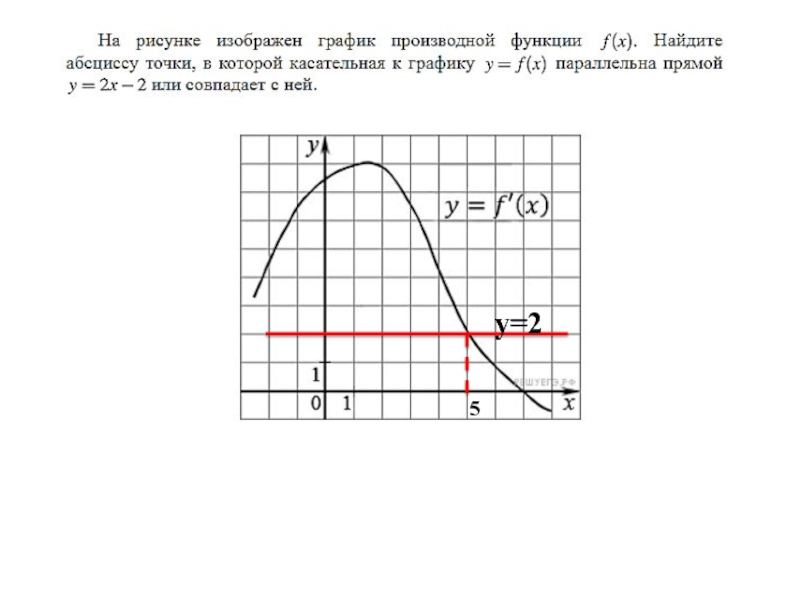
Слайд 16Примеры заданий
Поскольку касательная параллельна прямой y = −2x − 11 или совпадает с ней, их угловые
Слайд 23 На рисунке изображен график функции , определенной на интервале . Определите
Дан график функции
Теория:
F’(X)>0
, Следовательно ,
функция возрастает
Решение:
Найдем участки возрастания функции
(выделяем их последовательно на графике)
Выделяем соответствующие им
участки оси ОХ
- Найдем целые точки на этих отрезках
-Исключим точки, в которых производная равна нулю(в этих точках касательная параллельна оси ОХ) и еще исключим точки, являющиеся концами выделенных интервалов
- Считаем оставшиеся точки
Слайд 24 На рисунке изображен график функции , определенной на интервале . Определите количество
Дан график функции
Теория:
F’(X)<0
, cледовательно, функция убывает
Решение:
Найдем участки убывания функции
(выделяем их последовательно на графике)
Выделяем соответствующие им
участки оси ОХ
- Найдем целые точки на этих отрезках
-Исключим точки, в которых производная равна нулю(в этих точках касательная параллельна оси ОХ)
- Считаем оставшиеся точки
Слайд 26Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный.
Ответ:
Слайд 27
Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный.
Ответ: