- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проецирование поверхностей презентация
Содержание
- 1. Проецирование поверхностей
- 2. Проецирование поверхностей Поверхность – это множество последовательных
- 3. Проецирование поверхностей Способы задания поверхностей: Аналитический (поверхность
- 4. Проецирование поверхностей Линия, перемещающаяся в пространстве, называется
- 5. Проецирование поверхностей Очерк поверхности Контуром или контуром
- 6. Проецирование поверхностей Условие принадлежности точки поверхности Точка
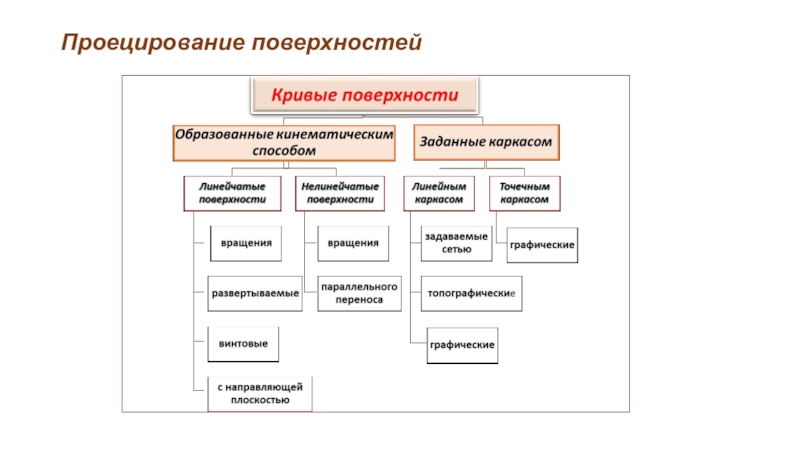
- 7. Проецирование поверхностей Классификация поверхностей Гранные поверхности
- 8. Проецирование поверхностей Примеры гранных поверхностей (параллелепипед, призма,
- 9. Проецирование поверхностей Наиболее часто встречающиеся гранные поверхности:
- 10. Проецирование поверхностей Пример построения проекций правильной прямой
- 11. Проецирование поверхностей Пример построения проекций пирамиды, в
- 12. Проецирование поверхностей
- 13. Проецирование поверхностей Поверхностью вращения называется поверхность, образованная
- 14. Проецирование поверхностей Основные параметры поверхности: образующая m;
- 15. Проецирование поверхностей Если ось вращения перпендикулярна горизонтальной
- 16. Проецирование поверхностей Если ось вращения перпендикулярна фронтальной
- 17. Проецирование поверхностей Характерные линии поверхности вращения Параллель
- 18. Проецирование поверхностей
- 19. Проецирование поверхностей Построение проекций точки А на
- 20. Проецирование поверхностей Алгоритм построения 1. Через проекцию
- 21. Проецирование поверхностей 3. По линии связи строят
- 22. Проецирование поверхностей Цилиндр вращения Цилиндром вращения называют
- 23. Проецирование поверхностей Конус вращения Конусом вращения (прямым
- 24. Проецирование поверхностей 1. Через проекцию точки К
- 25. Сфера Сферой называют поверхность, образованную вращением окружности
- 26. Проецирование поверхностей Алгоритм построения проекций точки 1.
- 27. Проецирование поверхностей Тор Тором называют поверхность, образованную
- 28. Проецирование поверхностей
- 29. Проецирование поверхностей Характерные линии сферы: экватор, горло,
- 30. Проецирование поверхностей
- 31. Проецирование поверхностей
- 32. Сечение поверхности плоскостью Сечение поверхности плоскостью представляет
- 33. Сечение поверхности плоскостью Построение проекций линии сечения
- 34. Сечение поверхности плоскостью Порядок построения точек :
- 35. Сечение поверхности плоскостью Построение проекций линии сечения
- 36. Сечение поверхности плоскостью 3. Строят проекции случайных
- 37. Сечение поверхности плоскостью Сечение конуса плоскостью Если
- 38. Сечение поверхности плоскостью Сечение конуса плоскостью Если
- 39. Сечение поверхности плоскостью Сечение конуса плоскостью Если
- 40. Сечение поверхности плоскостью Сечение конуса плоскостью Если
- 41. Сечение поверхности плоскостью Сечение конуса плоскостью Если
- 42. Пересечение прямой с поверхностью Точки пересечения прямой
- 43. Пересечение прямой с поверхностью Построение проекций точки
- 44. Пересечение прямой с поверхностью Если прямая является
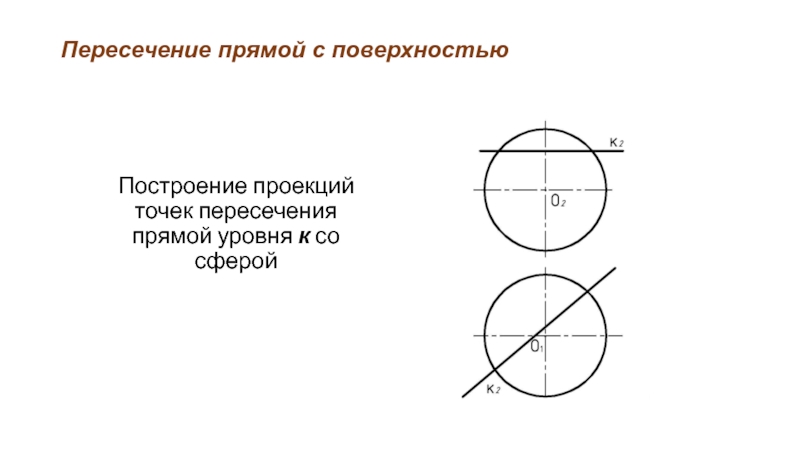
- 45. Пересечение прямой с поверхностью Построение проекций точек пересечения прямой уровня к со сферой
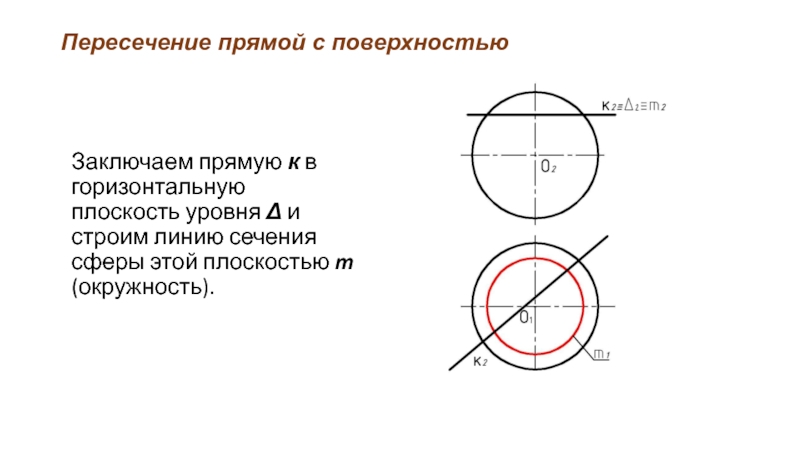
- 46. Пересечение прямой с поверхностью Заключаем прямую к
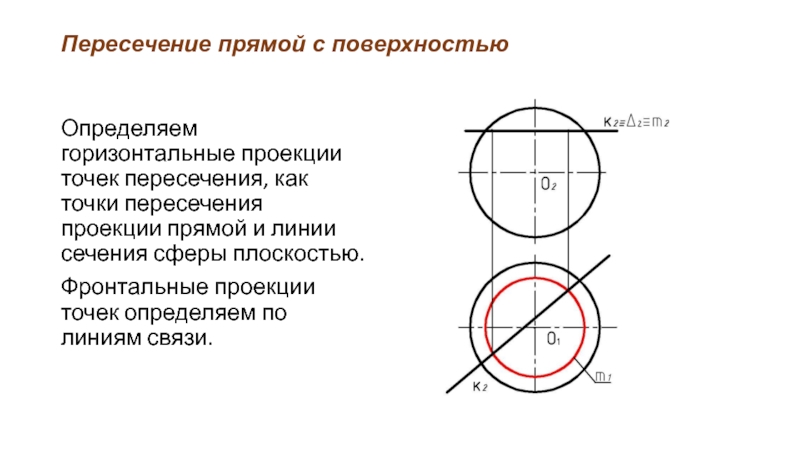
- 47. Пересечение прямой с поверхностью Определяем горизонтальные проекции
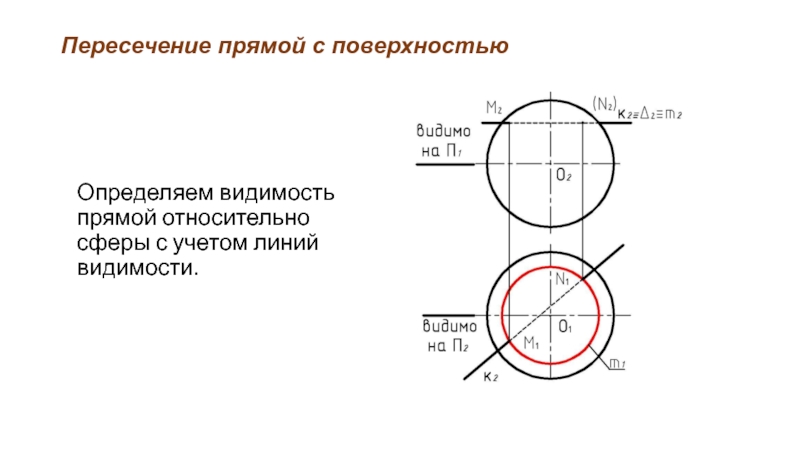
- 48. Пересечение прямой с поверхностью Определяем видимость прямой относительно сферы с учетом линий видимости.
Слайд 2Проецирование поверхностей
Поверхность – это множество последовательных положений линии, перемещающейся в пространстве
по определенному закону.
Слайд 3Проецирование поверхностей
Способы задания поверхностей:
Аналитический (поверхность задается уравнением, например, ax+by+cz=k - плоскость)
Каркасный
(поверхность задается семейством линий, лежащих на поверхности, пример – топографическая поверхность)
Кинематический (задается закон перемещения линии в пространстве):
поверхности второго порядка общего вида;
поверхности вращения;
винтовые поверхности;
поверхности с плоскостью параллелизма;
циклические поверхности.
Кинематический (задается закон перемещения линии в пространстве):
поверхности второго порядка общего вида;
поверхности вращения;
винтовые поверхности;
поверхности с плоскостью параллелизма;
циклические поверхности.
Слайд 4Проецирование поверхностей
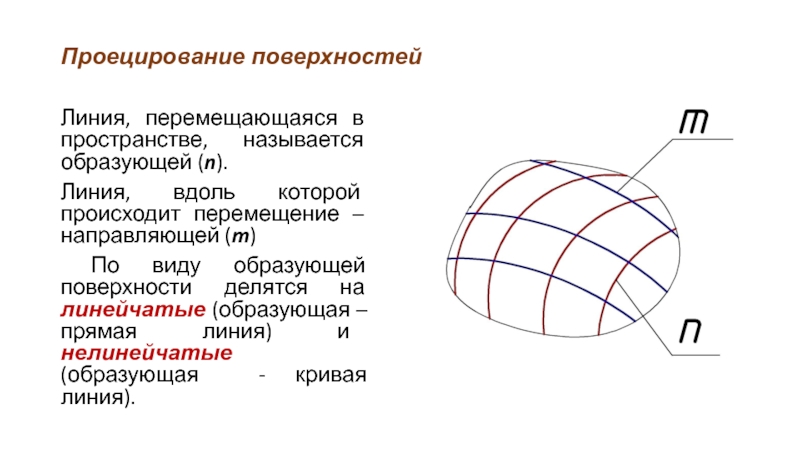
Линия, перемещающаяся в пространстве, называется образующей (n).
Линия, вдоль которой происходит
перемещение – направляющей (m)
По виду образующей поверхности делятся на линейчатые (образующая – прямая линия) и нелинейчатые (образующая - кривая линия).
По виду образующей поверхности делятся на линейчатые (образующая – прямая линия) и нелинейчатые (образующая - кривая линия).
Слайд 5Проецирование поверхностей
Очерк поверхности
Контуром или контуром видимости поверхности называется линия, точки которой
являются точками касания проецирующих прямых.
Очерком поверхности на плоскости проекций называется проекция контура на эту плоскость.
Линией видимости, которая является границей, отделяющей видимую часть поверхности от невидимой на данной плоскости проекций, называется проекция контурной линии (очерк).
Очерком поверхности на плоскости проекций называется проекция контура на эту плоскость.
Линией видимости, которая является границей, отделяющей видимую часть поверхности от невидимой на данной плоскости проекций, называется проекция контурной линии (очерк).
Слайд 6Проецирование поверхностей
Условие принадлежности точки поверхности
Точка принадлежит поверхности, если она принадлежит какой-либо
линии данной поверхности.
В качестве вспомогательных линий при построении точки используют графически простые линии (прямые и окружности), которые проецируются также в графически простые линии.
В качестве вспомогательных линий при построении точки используют графически простые линии (прямые и окружности), которые проецируются также в графически простые линии.
Слайд 7Проецирование поверхностей
Классификация поверхностей
Гранные поверхности (поверхности, образованные частями пересекающихся плоскостей)
Кривые поверхности
Слайд 8Проецирование поверхностей
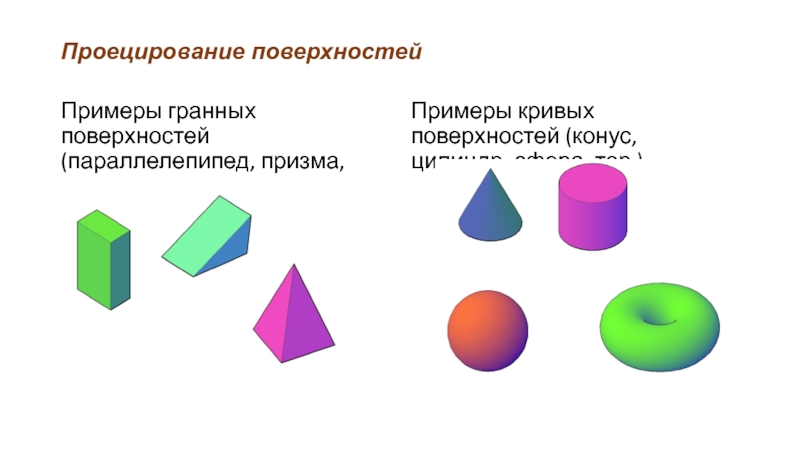
Примеры гранных поверхностей (параллелепипед, призма, пирамида,)
Примеры кривых поверхностей (конус, цилиндр,
сфера, тор )
Слайд 9Проецирование поверхностей
Наиболее часто встречающиеся гранные поверхности:
призма: в основании призмы лежит многоугольник,
а боковые грани – параллелограммы. Если ребра перпендикулярны основанию, то призма называется прямой, если в основании лежит правильный многоугольник – призма правильная;
пирамида: в основании пирамиды лежит многоугольник, боковые грани – треугольники, имеющие общую вершину;
призматоид: многогранник, у которого верхнее и нижнее основания многоугольники, лежащие в разных плоскостях;
правильные многогранники (тела Платона): многогранники, у которых все грани правильные и равные многоугольники, а углы при вершинах равны (тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр).
Построение проекций точки, принадлежащей гранной поверхности, аналогично построению проекций точки, принадлежащей плоскости.
пирамида: в основании пирамиды лежит многоугольник, боковые грани – треугольники, имеющие общую вершину;
призматоид: многогранник, у которого верхнее и нижнее основания многоугольники, лежащие в разных плоскостях;
правильные многогранники (тела Платона): многогранники, у которых все грани правильные и равные многоугольники, а углы при вершинах равны (тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр).
Построение проекций точки, принадлежащей гранной поверхности, аналогично построению проекций точки, принадлежащей плоскости.
Слайд 10Проецирование поверхностей
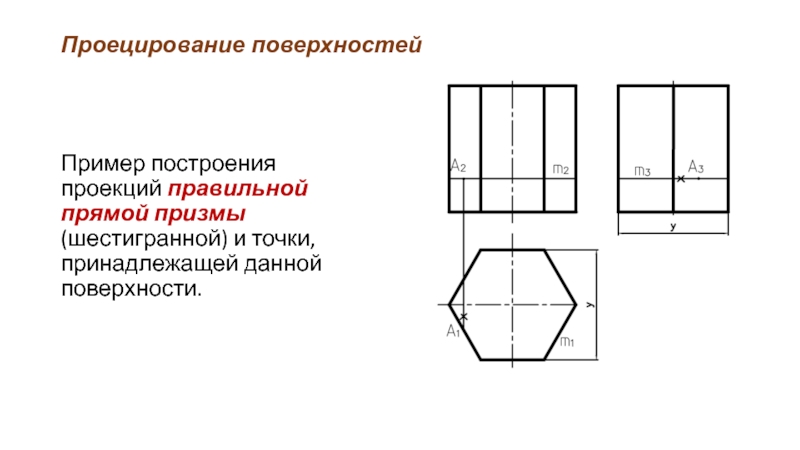
Пример построения проекций правильной прямой призмы (шестигранной) и точки, принадлежащей
данной поверхности.
Слайд 11Проецирование поверхностей
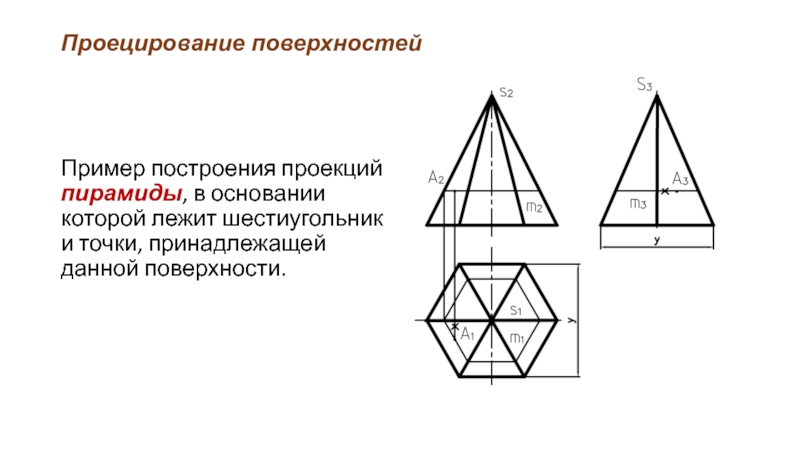
Пример построения проекций пирамиды, в основании которой лежит шестиугольник и
точки, принадлежащей данной поверхности.
Слайд 13Проецирование поверхностей
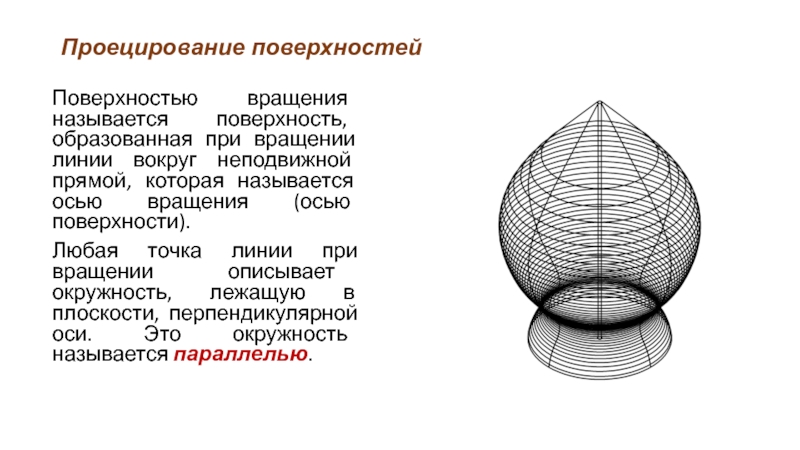
Поверхностью вращения называется поверхность, образованная при вращении линии вокруг неподвижной
прямой, которая называется осью вращения (осью поверхности).
Любая точка линии при вращении описывает окружность, лежащую в плоскости, перпендикулярной оси. Это окружность называется параллелью.
Любая точка линии при вращении описывает окружность, лежащую в плоскости, перпендикулярной оси. Это окружность называется параллелью.
Слайд 14Проецирование поверхностей
Основные параметры поверхности:
образующая m;
ось вращения I;
точка А, принадлежащая образующей
и, следовательно, поверхности;
параллель n, лежащая в плоскости, перпендикулярной оси;
меридиан (линия, образованная при рассечении поверхности плоскостью, проходящей через ось).
параллель n, лежащая в плоскости, перпендикулярной оси;
меридиан (линия, образованная при рассечении поверхности плоскостью, проходящей через ось).
Слайд 15Проецирование поверхностей
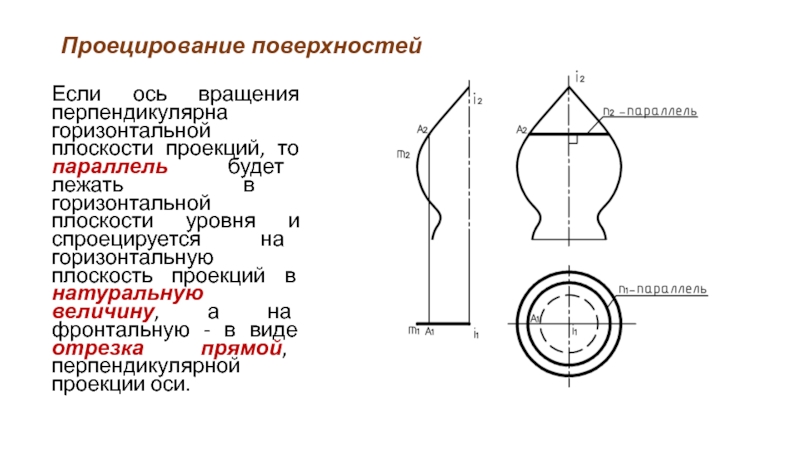
Если ось вращения перпендикулярна горизонтальной плоскости проекций, то параллель будет
лежать в горизонтальной плоскости уровня и спроецируется на горизонтальную плоскость проекций в натуральную величину, а на фронтальную - в виде отрезка прямой, перпендикулярной проекции оси.
Слайд 16Проецирование поверхностей
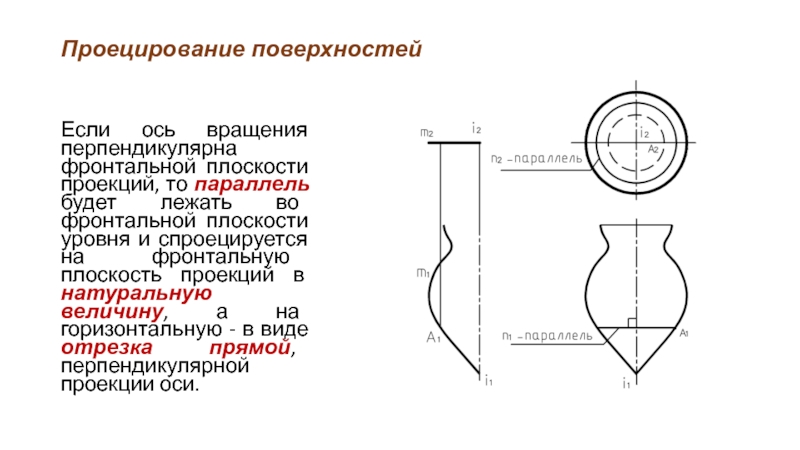
Если ось вращения перпендикулярна фронтальной плоскости проекций, то параллель будет
лежать во фронтальной плоскости уровня и спроецируется на фронтальную плоскость проекций в натуральную величину, а на горизонтальную - в виде отрезка прямой, перпендикулярной проекции оси.
Слайд 17Проецирование поверхностей
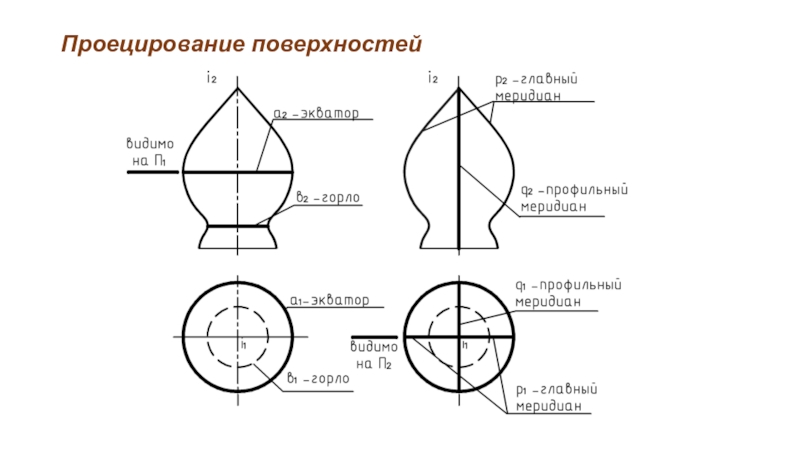
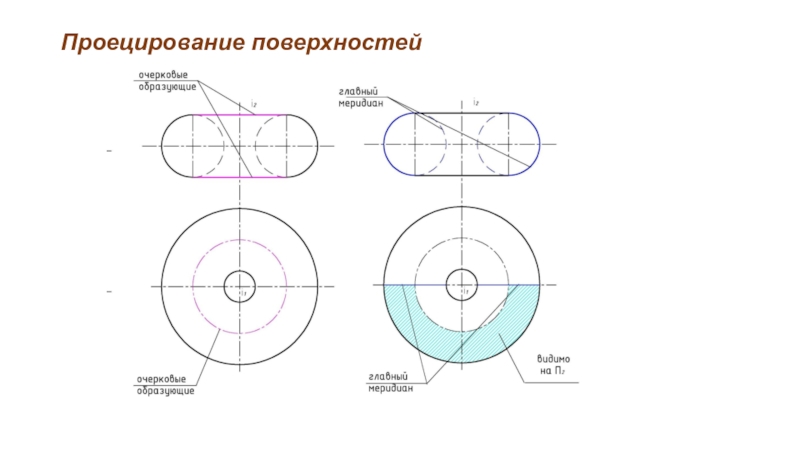
Характерные линии поверхности вращения
Параллель наибольшего радиуса называется экватором.
Параллель наименьшего радиуса
называется горлом.
Меридиан, расположенный в плоскости, параллельной плоскости проекций, называется главным меридианом.
Меридиан, лежащий во фронтальной плоскости уровня называется фронтальным.
Меридиан, лежащий в профильной плоскости уровня называется профильным.
Проекции экватора и главных меридианов являются, как правило, очерками поверхности (линиями видимости).
Меридиан, расположенный в плоскости, параллельной плоскости проекций, называется главным меридианом.
Меридиан, лежащий во фронтальной плоскости уровня называется фронтальным.
Меридиан, лежащий в профильной плоскости уровня называется профильным.
Проекции экватора и главных меридианов являются, как правило, очерками поверхности (линиями видимости).
Слайд 19Проецирование поверхностей
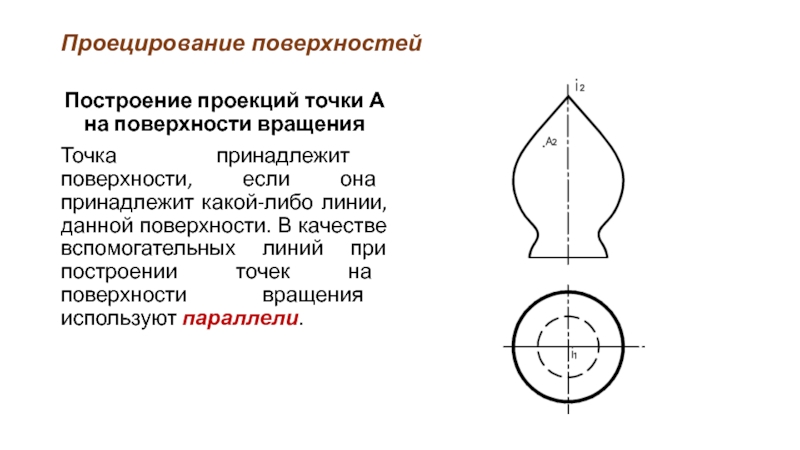
Построение проекций точки А на поверхности вращения
Точка принадлежит поверхности, если
она принадлежит какой-либо линии, данной поверхности. В качестве вспомогательных линий при построении точек на поверхности вращения используют параллели.
Слайд 20Проецирование поверхностей
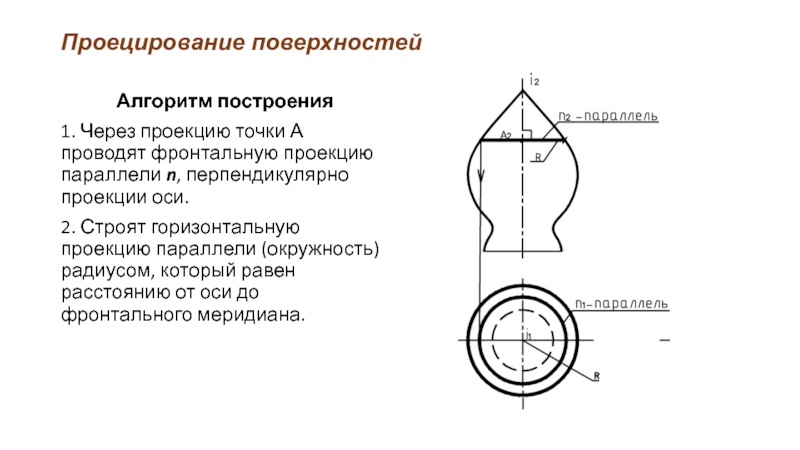
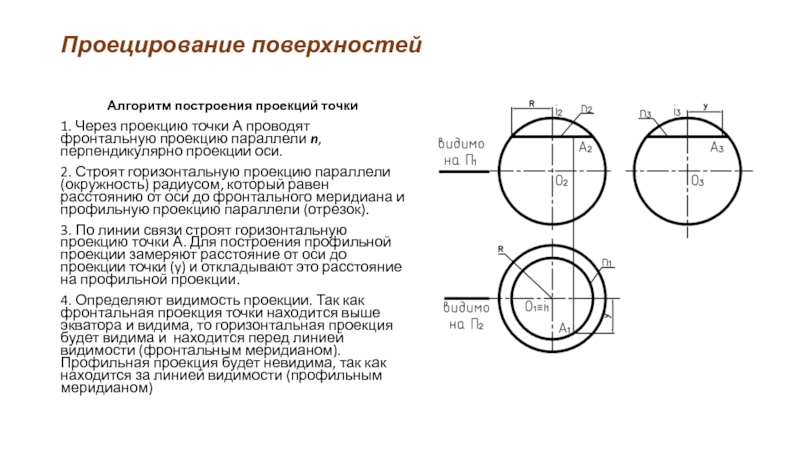
Алгоритм построения
1. Через проекцию точки А проводят фронтальную проекцию параллели
n, перпендикулярно проекции оси.
2. Строят горизонтальную проекцию параллели (окружность) радиусом, который равен расстоянию от оси до фронтального меридиана.
2. Строят горизонтальную проекцию параллели (окружность) радиусом, который равен расстоянию от оси до фронтального меридиана.
Слайд 21Проецирование поверхностей
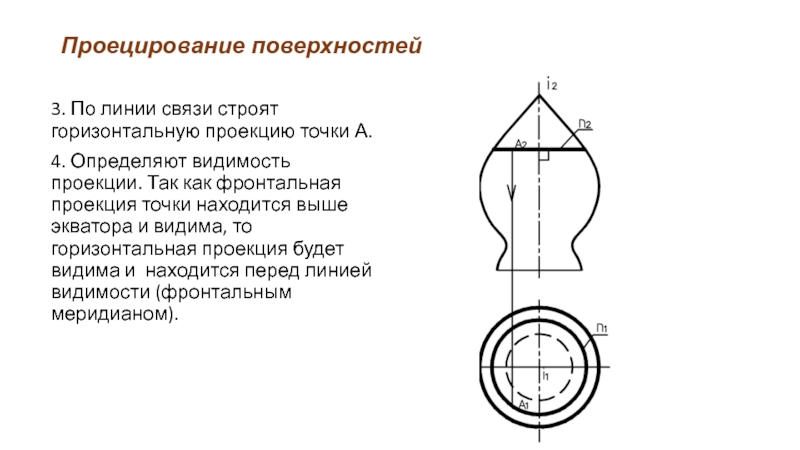
3. По линии связи строят горизонтальную проекцию точки А.
4. Определяют
видимость проекции. Так как фронтальная проекция точки находится выше экватора и видима, то горизонтальная проекция будет видима и находится перед линией видимости (фронтальным меридианом).
Слайд 22Проецирование поверхностей
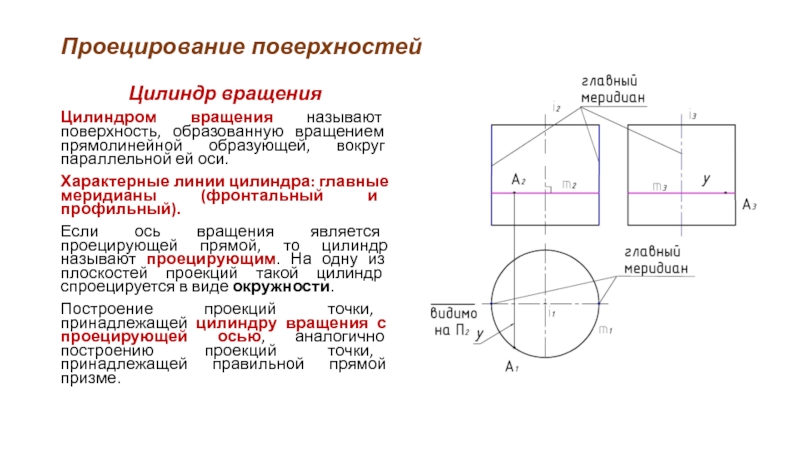
Цилиндр вращения
Цилиндром вращения называют поверхность, образованную вращением прямолинейной образующей, вокруг
параллельной ей оси.
Характерные линии цилиндра: главные меридианы (фронтальный и профильный).
Если ось вращения является проецирующей прямой, то цилиндр называют проецирующим. На одну из плоскостей проекций такой цилиндр спроецируется в виде окружности.
Построение проекций точки, принадлежащей цилиндру вращения с проецирующей осью, аналогично построению проекций точки, принадлежащей правильной прямой призме.
Характерные линии цилиндра: главные меридианы (фронтальный и профильный).
Если ось вращения является проецирующей прямой, то цилиндр называют проецирующим. На одну из плоскостей проекций такой цилиндр спроецируется в виде окружности.
Построение проекций точки, принадлежащей цилиндру вращения с проецирующей осью, аналогично построению проекций точки, принадлежащей правильной прямой призме.
Слайд 23Проецирование поверхностей
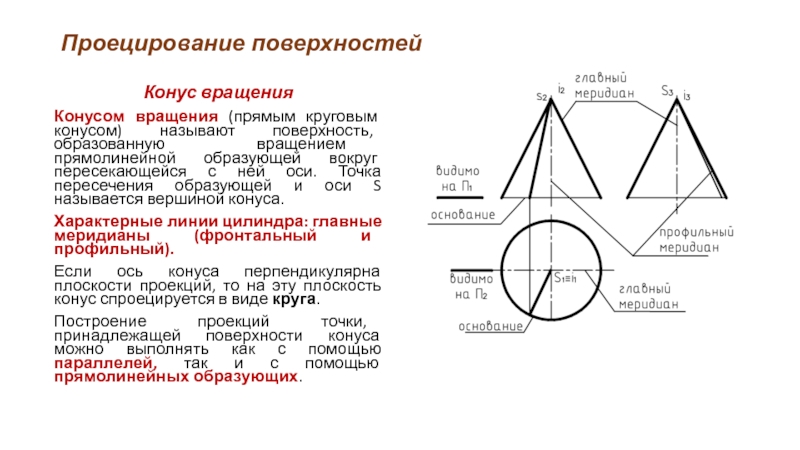
Конус вращения
Конусом вращения (прямым круговым конусом) называют поверхность, образованную вращением
прямолинейной образующей вокруг пересекающейся с ней оси. Точка пересечения образующей и оси S называется вершиной конуса.
Характерные линии цилиндра: главные меридианы (фронтальный и профильный).
Если ось конуса перпендикулярна плоскости проекций, то на эту плоскость конус спроецируется в виде круга.
Построение проекций точки, принадлежащей поверхности конуса можно выполнять как с помощью параллелей, так и с помощью прямолинейных образующих.
Характерные линии цилиндра: главные меридианы (фронтальный и профильный).
Если ось конуса перпендикулярна плоскости проекций, то на эту плоскость конус спроецируется в виде круга.
Построение проекций точки, принадлежащей поверхности конуса можно выполнять как с помощью параллелей, так и с помощью прямолинейных образующих.
Слайд 24Проецирование поверхностей
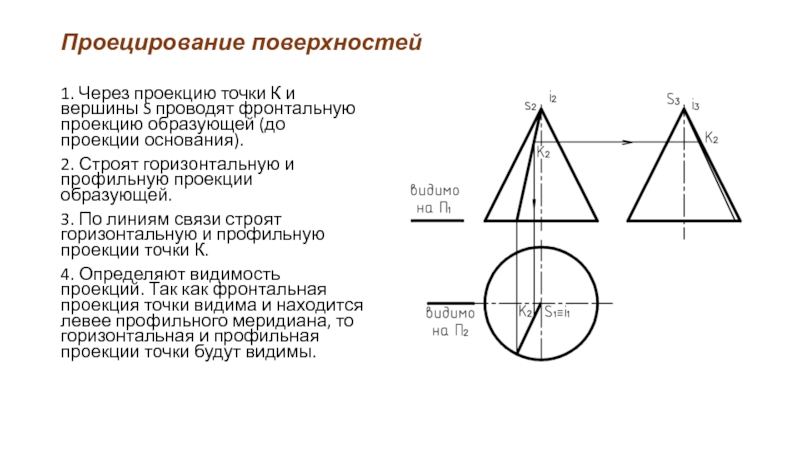
1. Через проекцию точки К и вершины S проводят фронтальную
проекцию образующей (до проекции основания).
2. Строят горизонтальную и профильную проекции образующей.
3. По линиям связи строят горизонтальную и профильную проекции точки К.
4. Определяют видимость проекций. Так как фронтальная проекция точки видима и находится левее профильного меридиана, то горизонтальная и профильная проекции точки будут видимы.
2. Строят горизонтальную и профильную проекции образующей.
3. По линиям связи строят горизонтальную и профильную проекции точки К.
4. Определяют видимость проекций. Так как фронтальная проекция точки видима и находится левее профильного меридиана, то горизонтальная и профильная проекции точки будут видимы.
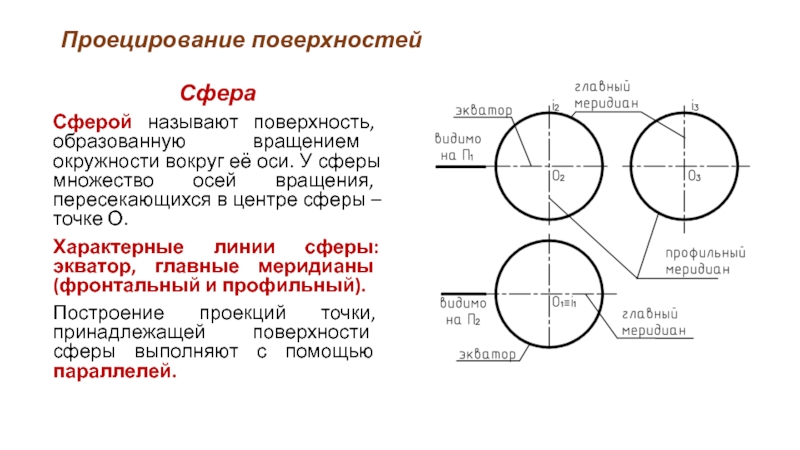
Слайд 25Сфера
Сферой называют поверхность, образованную вращением окружности вокруг её оси. У сферы
множество осей вращения, пересекающихся в центре сферы – точке О.
Характерные линии сферы: экватор, главные меридианы (фронтальный и профильный).
Построение проекций точки, принадлежащей поверхности сферы выполняют с помощью параллелей.
Характерные линии сферы: экватор, главные меридианы (фронтальный и профильный).
Построение проекций точки, принадлежащей поверхности сферы выполняют с помощью параллелей.
Проецирование поверхностей
Слайд 26Проецирование поверхностей
Алгоритм построения проекций точки
1. Через проекцию точки А проводят фронтальную
проекцию параллели n, перпендикулярно проекции оси.
2. Строят горизонтальную проекцию параллели (окружность) радиусом, который равен расстоянию от оси до фронтального меридиана и профильную проекцию параллели (отрезок).
3. По линии связи строят горизонтальную проекцию точки А. Для построения профильной проекции замеряют расстояние от оси до проекции точки (y) и откладывают это расстояние на профильной проекции.
4. Определяют видимость проекции. Так как фронтальная проекция точки находится выше экватора и видима, то горизонтальная проекция будет видима и находится перед линией видимости (фронтальным меридианом). Профильная проекция будет невидима, так как находится за линией видимости (профильным меридианом)
2. Строят горизонтальную проекцию параллели (окружность) радиусом, который равен расстоянию от оси до фронтального меридиана и профильную проекцию параллели (отрезок).
3. По линии связи строят горизонтальную проекцию точки А. Для построения профильной проекции замеряют расстояние от оси до проекции точки (y) и откладывают это расстояние на профильной проекции.
4. Определяют видимость проекции. Так как фронтальная проекция точки находится выше экватора и видима, то горизонтальная проекция будет видима и находится перед линией видимости (фронтальным меридианом). Профильная проекция будет невидима, так как находится за линией видимости (профильным меридианом)
Слайд 27Проецирование поверхностей
Тор
Тором называют поверхность, образованную вращение окружности или ее дуги, вокруг
оси, не проходящей через центр окружности, но лежащей в плоскости образующей окружности.
Тор бывает:
открытым (круговое кольцо) – окружность не пересекает ось;
закрытым – окружность касается оси;
самопересекающимся – окружность пересекает ось.
Тор бывает:
открытым (круговое кольцо) – окружность не пересекает ось;
закрытым – окружность касается оси;
самопересекающимся – окружность пересекает ось.
Слайд 29Проецирование поверхностей
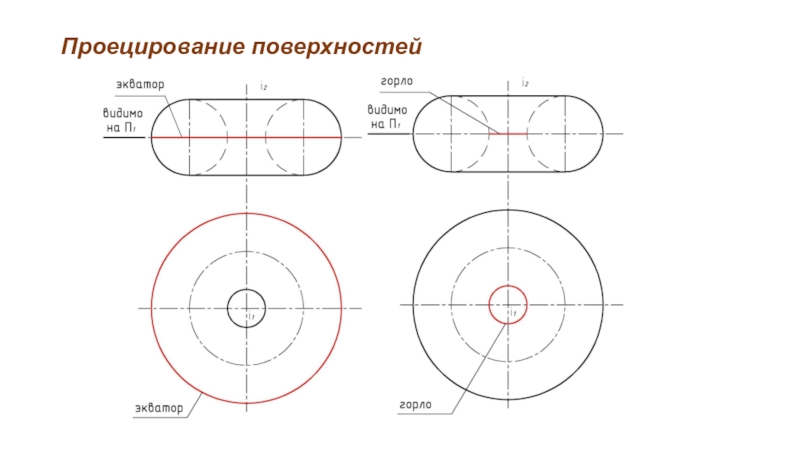
Характерные линии сферы: экватор, горло, главные меридианы (фронтальный и профильный),
верхняя и нижняя очерковые образующие (параллели).
Для открытого тора проекции очерка и главных меридианов не совпадают.
Построение проекций точки, принадлежащей поверхности тора выполняют с помощью параллелей.
Для открытого тора проекции очерка и главных меридианов не совпадают.
Построение проекций точки, принадлежащей поверхности тора выполняют с помощью параллелей.
Слайд 32Сечение поверхности плоскостью
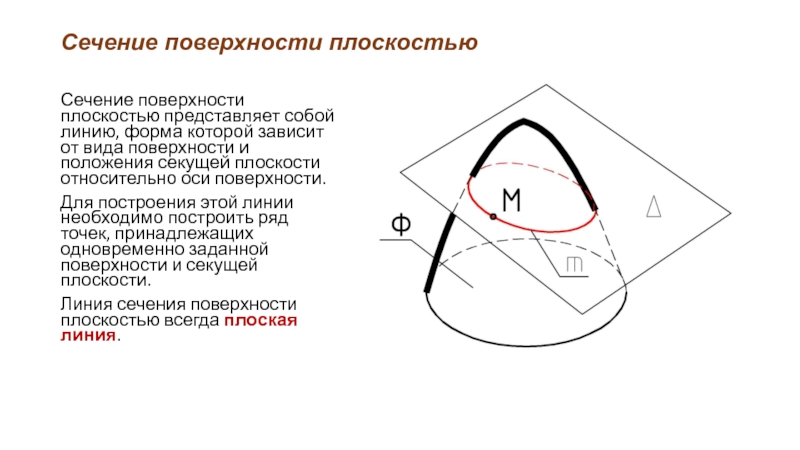
Сечение поверхности плоскостью представляет собой линию, форма которой зависит
от вида поверхности и положения секущей плоскости относительно оси поверхности.
Для построения этой линии необходимо построить ряд точек, принадлежащих одновременно заданной поверхности и секущей плоскости.
Линия сечения поверхности плоскостью всегда плоская линия.
Для построения этой линии необходимо построить ряд точек, принадлежащих одновременно заданной поверхности и секущей плоскости.
Линия сечения поверхности плоскостью всегда плоская линия.
Слайд 33Сечение поверхности плоскостью
Построение проекций линии сечения поверхности плоскостью аналогично построению проекций
линии пересечения двух плоскостей:
если плоскость занимает частное положение (плоскость уровня или проецирующая), то одна проекция линии сечения определяется сразу, а вторая строится по принадлежности точки поверхности;
если плоскость является плоскостью общего положения, то вводят вспомогательные плоскости частного положения (обычно плоскости уровня), пересекающие заданные плоскость и поверхность по графически простым линиям, определяют точки пересечения линий сечения.
если плоскость занимает частное положение (плоскость уровня или проецирующая), то одна проекция линии сечения определяется сразу, а вторая строится по принадлежности точки поверхности;
если плоскость является плоскостью общего положения, то вводят вспомогательные плоскости частного положения (обычно плоскости уровня), пересекающие заданные плоскость и поверхность по графически простым линиям, определяют точки пересечения линий сечения.
Слайд 34Сечение поверхности плоскостью
Порядок построения точек :
Экстремальные точки (высшая, низшая, крайние левая
и правая, ближайшая и наиболее удаленная).
Очерковые, лежащие на линиях видимости.
Промежуточные или случайные.
Первые две группы точек обозначают на чертеже буквами, третью – цифрами.
Очерковые, лежащие на линиях видимости.
Промежуточные или случайные.
Первые две группы точек обозначают на чертеже буквами, третью – цифрами.
Слайд 35Сечение поверхности плоскостью
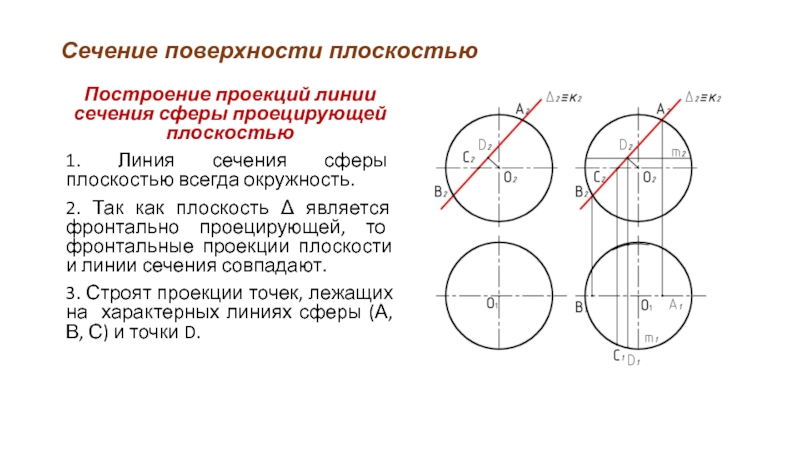
Построение проекций линии сечения сферы проецирующей плоскостью
1. Линия сечения
сферы плоскостью всегда окружность.
2. Так как плоскость Δ является фронтально проецирующей, то фронтальные проекции плоскости и линии сечения совпадают.
3. Строят проекции точек, лежащих на характерных линиях сферы (А, В, С) и точки D.
2. Так как плоскость Δ является фронтально проецирующей, то фронтальные проекции плоскости и линии сечения совпадают.
3. Строят проекции точек, лежащих на характерных линиях сферы (А, В, С) и точки D.
Слайд 36Сечение поверхности плоскостью
3. Строят проекции случайных точек 1 и 2 по
принадлежности поверхности сферы (с помощью параллелей).
4. Соединяют полученные проекции точек плавной линией с учетом видимости.
4. Соединяют полученные проекции точек плавной линией с учетом видимости.
Слайд 37Сечение поверхности плоскостью
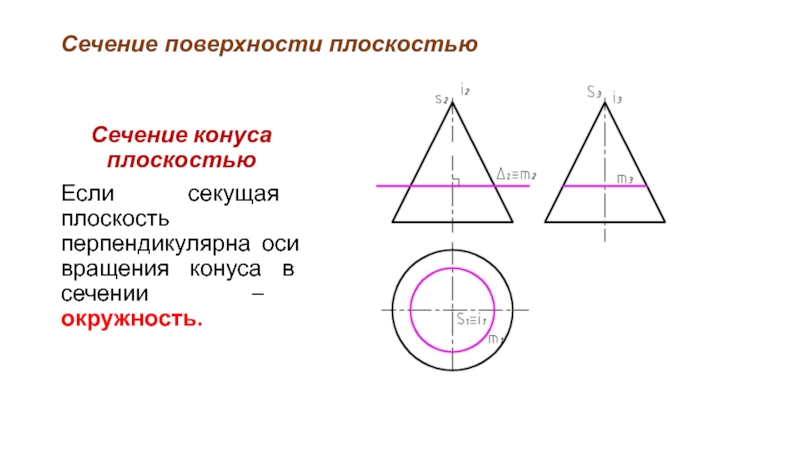
Сечение конуса плоскостью
Если секущая плоскость перпендикулярна оси вращения конуса
в сечении – окружность.
Слайд 38Сечение поверхности плоскостью
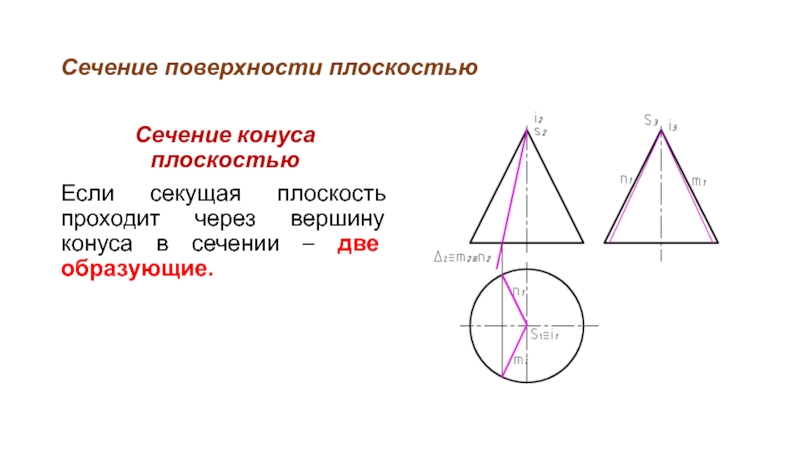
Сечение конуса плоскостью
Если секущая плоскость проходит через вершину конуса
в сечении – две образующие.
Слайд 39Сечение поверхности плоскостью
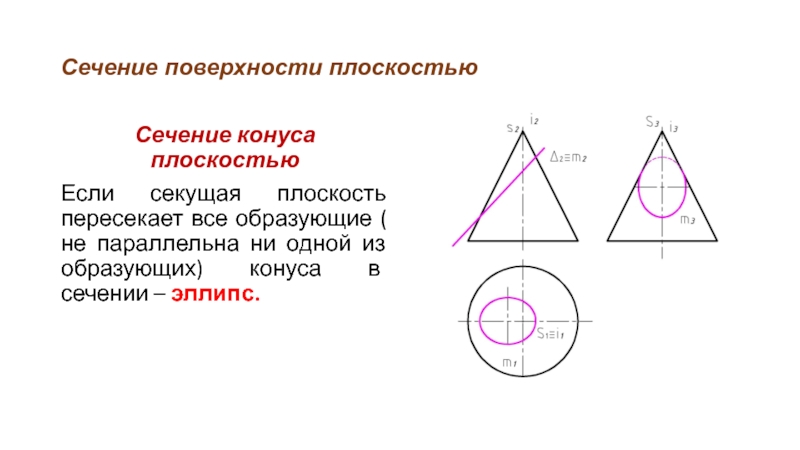
Сечение конуса плоскостью
Если секущая плоскость пересекает все образующие (
не параллельна ни одной из образующих) конуса в сечении – эллипс.
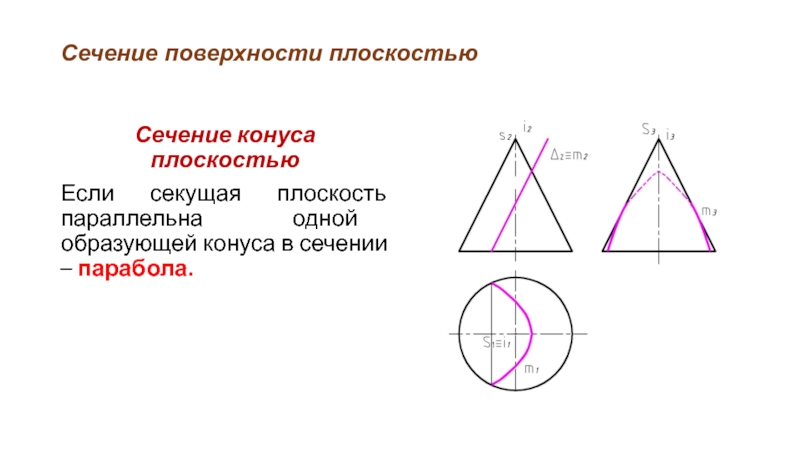
Слайд 40Сечение поверхности плоскостью
Сечение конуса плоскостью
Если секущая плоскость параллельна одной образующей конуса
в сечении – парабола.
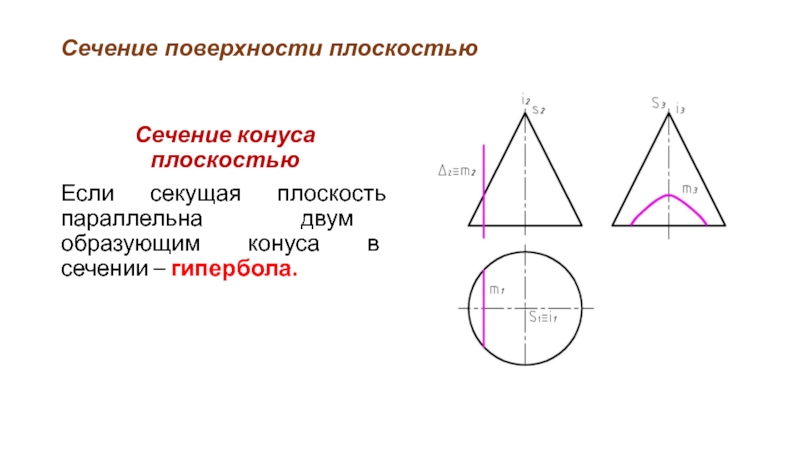
Слайд 41Сечение поверхности плоскостью
Сечение конуса плоскостью
Если секущая плоскость параллельна двум образующим конуса
в сечении – гипербола.
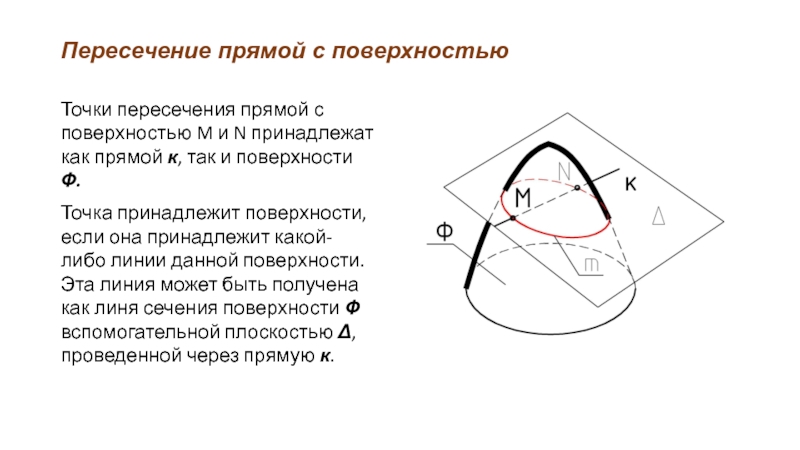
Слайд 42Пересечение прямой с поверхностью
Точки пересечения прямой с поверхностью M и N
принадлежат как прямой к, так и поверхности Ф.
Точка принадлежит поверхности, если она принадлежит какой-либо линии данной поверхности. Эта линия может быть получена как линя сечения поверхности Ф вспомогательной плоскостью Δ, проведенной через прямую к.
Точка принадлежит поверхности, если она принадлежит какой-либо линии данной поверхности. Эта линия может быть получена как линя сечения поверхности Ф вспомогательной плоскостью Δ, проведенной через прямую к.
Слайд 43Пересечение прямой с поверхностью
Построение проекций точки пересечения прямой общего положения или
прямой уровня с поверхностью выполняется по следующему алгоритму:
Заключаем прямую во вспомогательную плоскость, пересекающую поверхность по графически простым линиям (плоскость может быть как плоскостью уровня, так и плоскостью общего положения для линейчатых поверхностей)
Строим проекции линии сечения поверхности плоскостью.
Определяем точку пересечения заданной прямой и построенной линии сечения.
Определяем видимость прямой относительно поверхности с учетом линий видимости.
Заключаем прямую во вспомогательную плоскость, пересекающую поверхность по графически простым линиям (плоскость может быть как плоскостью уровня, так и плоскостью общего положения для линейчатых поверхностей)
Строим проекции линии сечения поверхности плоскостью.
Определяем точку пересечения заданной прямой и построенной линии сечения.
Определяем видимость прямой относительно поверхности с учетом линий видимости.
Слайд 44Пересечение прямой с поверхностью
Если прямая является проецирующей, то одна проекция точек
пересечения прямой с поверхностью определяется сразу, в вторая строится по принадлежности точки поверхности.
Слайд 45Пересечение прямой с поверхностью
Построение проекций точек пересечения прямой уровня к со
сферой
Слайд 46Пересечение прямой с поверхностью
Заключаем прямую к в горизонтальную плоскость уровня Δ
и строим линию сечения сферы этой плоскостью m (окружность).
Слайд 47Пересечение прямой с поверхностью
Определяем горизонтальные проекции точек пересечения, как точки пересечения
проекции прямой и линии сечения сферы плоскостью.
Фронтальные проекции точек определяем по линиям связи.
Фронтальные проекции точек определяем по линиям связи.
Слайд 48Пересечение прямой с поверхностью
Определяем видимость прямой относительно сферы с учетом линий
видимости.