- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проекции с числовыми отметками презентация
Содержание
- 1. Проекции с числовыми отметками
- 2. Проекции с числовыми отметками Сущность метода заключается
- 3. Проекции с числовыми отметками Терминология проекций с
- 4. Проекции с числовыми отметками Планы сопровождают линейным
- 5. Проекции с числовыми отметками (проецирование точек )
- 6. Проекции с числовыми отметками (проецирование точек) Наглядное изображение Проекции точек
- 7. Проекции с числовыми отметками (проецирование прямых) Разность
- 8. Проекции с числовыми отметками (проецирование прямых) Уклон
- 9. Проекции с числовыми отметками (проецирование прямых) Интервал
- 10. Проекции с числовыми отметками (проецирование прямых) Интервал
- 11. Проекции с числовыми отметками (проецирование прямых) Прямую
- 12. Проекции с числовыми отметками (проецирование прямых)
- 13. Проекции с числовыми отметками (проецирование прямых) Прямая
- 14. Проекции с числовыми отметками (проецирование прямых) Если
- 15. Проекции с числовыми отметками (проецирование прямых) Прямые
- 16. Проекции с числовыми отметками (проецирование прямых) Прямые
- 17. Проекции с числовыми отметками (проецирование прямых) Если
- 18. Проекции с числовыми отметками (проецирование плоскостей) Масштаб
- 19. Проекции с числовыми отметками (проецирование плоскостей) Интервал
- 20. Проекции с числовыми отметками (проецирование плоскостей) Угол
- 21. Проекции с числовыми отметками (проецирование плоскостей)
- 22. Проекции с числовыми отметками (проецирование плоскостей)
- 23. Проекции с числовыми отметками (проецирование плоскостей) Плоскость в проекциях с числовыми отметками задают:
- 24. Проекции с числовыми отметками (проецирование плоскостей) Проекциями трех точек
- 25. Проекции с числовыми отметками (проецирование плоскостей) Проекциями
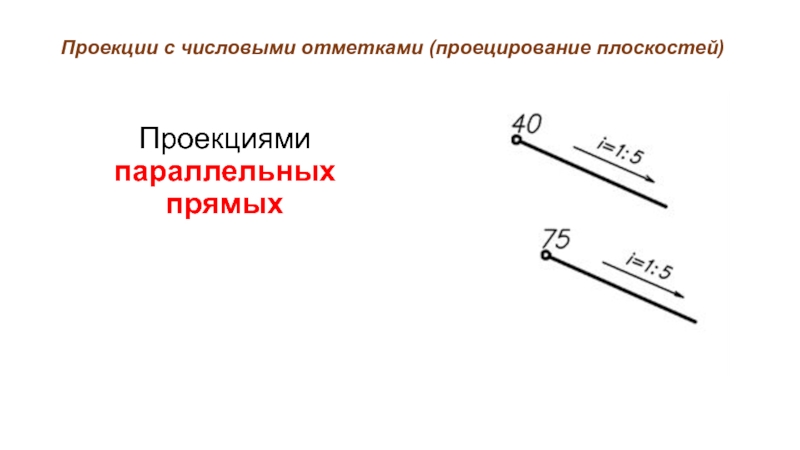
- 26. Проекции с числовыми отметками (проецирование плоскостей) Проекциями параллельных прямых
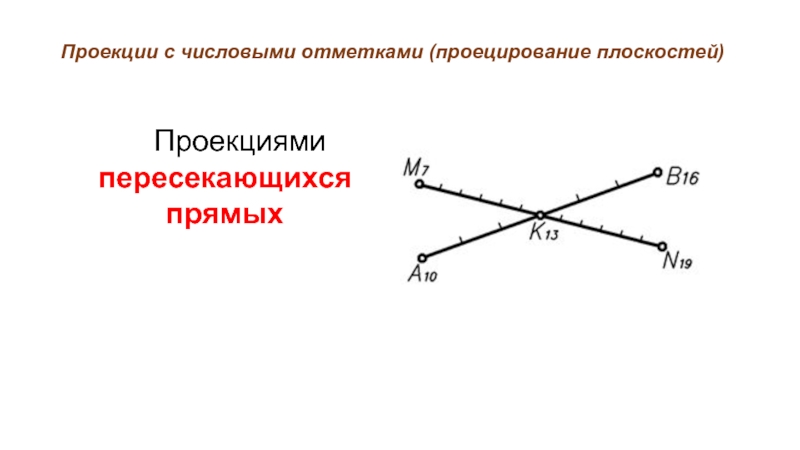
- 27. Проекции с числовыми отметками (проецирование плоскостей) Проекциями пересекающихся прямых
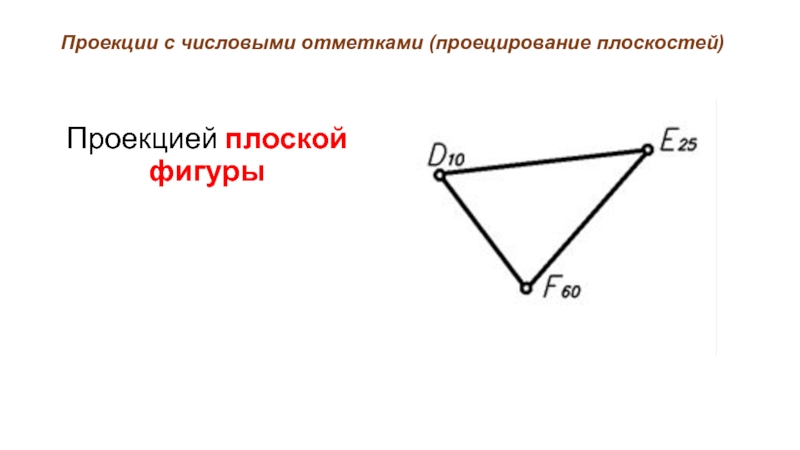
- 28. Проекции с числовыми отметками (проецирование плоскостей) Проекцией плоской фигуры
- 29. Проекции с числовыми отметками Масштабом уклона плоскости (наиболее часто встречающийся и удобный способ)
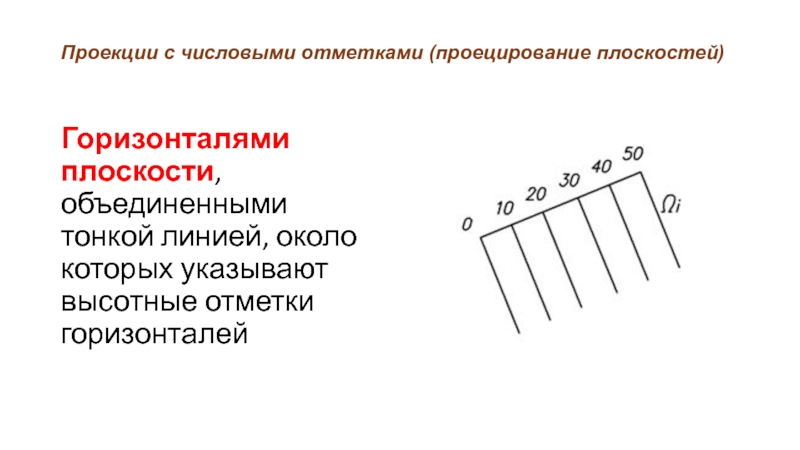
- 30. Проекции с числовыми отметками (проецирование плоскостей) Горизонталями
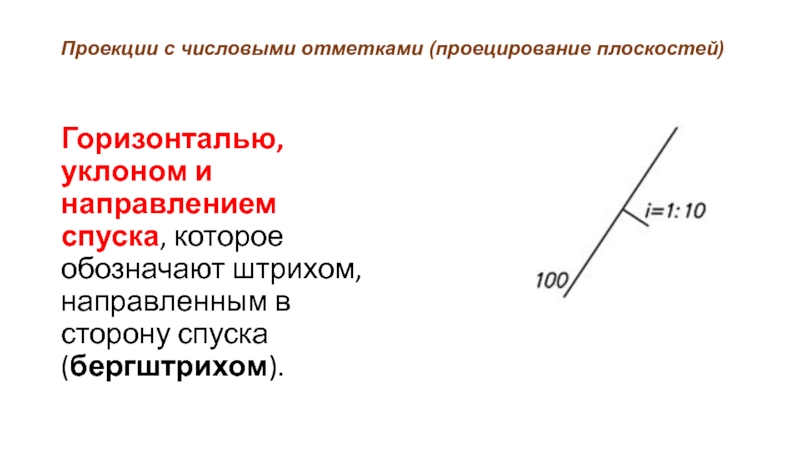
- 31. Проекции с числовыми отметками (проецирование плоскостей) Горизонталью,
- 32. Проекции с числовыми отметками (взаимное расположение прямых
- 33. Проекции с числовыми отметками (взаимное расположение прямых
- 34. Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
- 35. Проекции с числовыми отметками (взаимное расположение прямых
- 36. Проекции с числовыми отметками (взаимное расположение прямых
- 37. Проекции с числовыми отметками (взаимное расположение прямых
- 38. Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
- 39. Проекции с числовыми отметками (взаимное расположение прямых
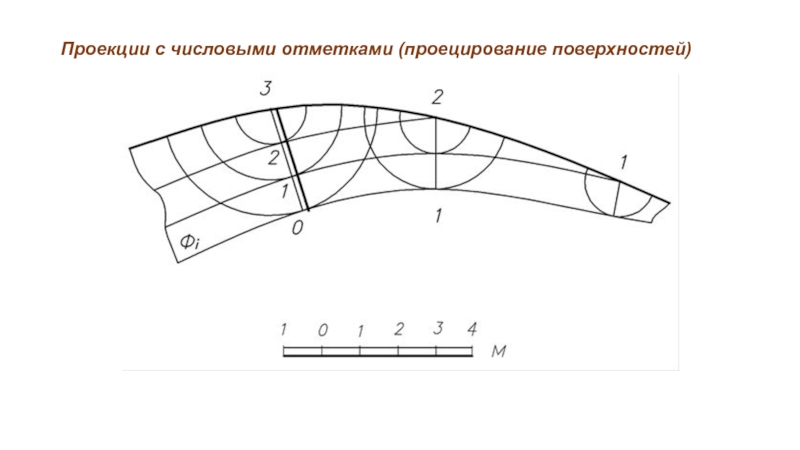
- 40. Проекции с числовыми отметками (проецирование поверхностей) Гранные
- 41. Проекции с числовыми отметками (проецирование поверхностей) Линией
- 42. Проекции с числовыми отметками (проецирование поверхностей) Гранные поверхности
- 43. Проекции с числовыми отметками (проецирование поверхностей) Конические
- 44. Проекции с числовыми отметками (проецирование поверхностей)
- 45. Проекции с числовыми отметками (проецирование поверхностей) Поверхность
- 46. Проекции с числовыми отметками (проецирование поверхностей)
- 47. Проекции с числовыми отметками (проецирование поверхностей) Проекция
- 48. Проекции с числовыми отметками (проецирование поверхностей)
- 49. Проекции с числовыми отметками (проецирование поверхностей) Топографическая
- 50. Проекции с числовыми отметками (проецирование поверхностей)
- 51. Проекции с числовыми отметками (проецирование поверхностей) Основные
- 52. Проекции с числовыми отметками (взаимное расположение прямых,
- 53. Проекции с числовыми отметками (взаимное расположение прямых,
- 54. Проекции с числовыми отметками (взаимное расположение прямых,
- 55. Проекции с числовыми отметками (взаимное расположение прямых,
- 56. Проекции с числовыми отметками (взаимное расположение прямых,
- 57. Проекции с числовыми отметками (взаимное расположение прямых,
- 58. Проекции с числовыми отметками (взаимное расположение прямых,
- 59. Проекции с числовыми отметками (взаимное расположение прямых,
- 60. Проекции с числовыми отметками (взаимное расположение прямых,
- 61. Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей) Построение линии пересечения двух топографических поверхностей
- 62. Проекции с числовыми отметками (взаимное расположение прямых,
- 63. Проекции с числовыми отметками (взаимное расположение прямых,
- 64. Проекции с числовыми отметками (взаимное расположение прямых,
- 65. Проекции с числовыми отметками (взаимное расположение прямых,
Слайд 2Проекции с числовыми отметками
Сущность метода заключается в прямоугольном проецировании объекта на
горизонтальную плоскость проекций с указанием числа, показывающего на сколько единиц длины удалены характерные точки объекта от плоскости проекций (как правило, в метрах).
Слайд 3Проекции с числовыми отметками
Терминология проекций с числовыми отметками:
Горизонтальная плоскость, на которую
осуществляется проецирование - плоскость нулевого уровня.
Горизонтальная проекция объекта – план.
Число, указывающее расстояние до плоскости нулевого уровня, - отметка (альтитуда).
При изображении топографической поверхности за плоскость нулевого уровня принимают поверхность уровня моря.
Горизонтальная проекция объекта – план.
Число, указывающее расстояние до плоскости нулевого уровня, - отметка (альтитуда).
При изображении топографической поверхности за плоскость нулевого уровня принимают поверхность уровня моря.
Слайд 4Проекции с числовыми отметками
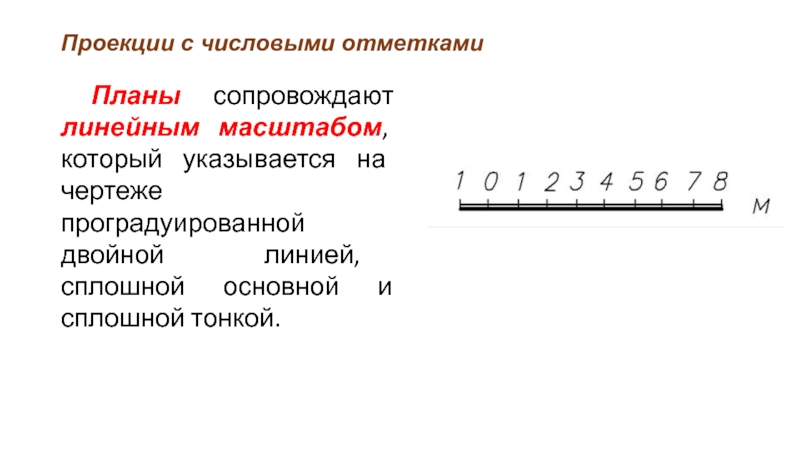
Планы сопровождают линейным масштабом, который указывается на чертеже
проградуированной двойной линией, сплошной основной и сплошной тонкой.
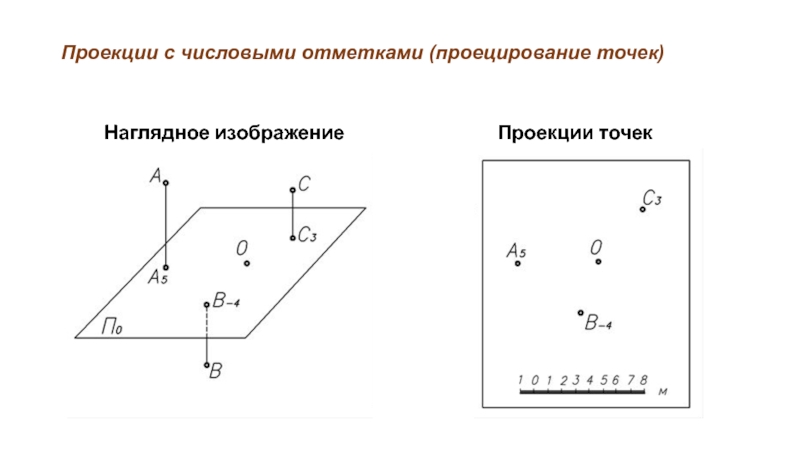
Слайд 5Проекции с числовыми отметками (проецирование точек )
Проекцией точки в проекциях с
числовыми отметками является точка, обозначенная либо буквой, рядом с которой ставится отметка этой точки, либо самой отметкой.
Точки, находящиеся ниже плоскости нулевого уровня, имеют отрицательные отметки, которые пишутся со знаком минус.
Точки, находящиеся ниже плоскости нулевого уровня, имеют отрицательные отметки, которые пишутся со знаком минус.
Слайд 7Проекции с числовыми отметками (проецирование прямых)
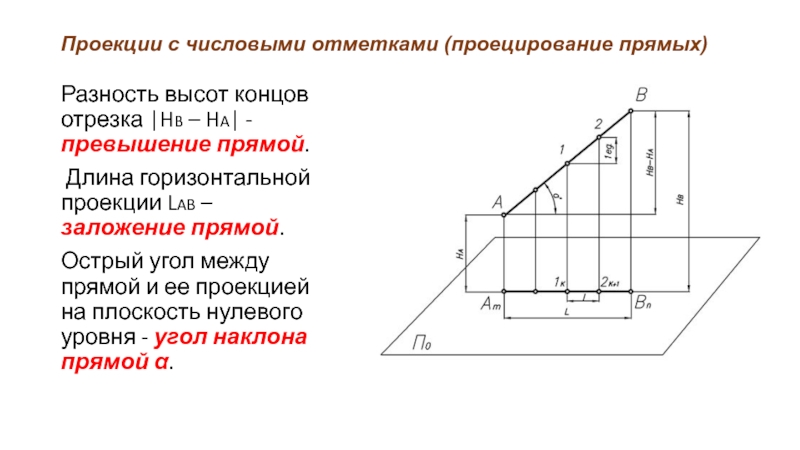
Разность высот концов отрезка |HB –
HA| - превышение прямой.
Длина горизонтальной проекции LAB – заложение прямой.
Острый угол между прямой и ее проекцией на плоскость нулевого уровня - угол наклона прямой α.
Длина горизонтальной проекции LAB – заложение прямой.
Острый угол между прямой и ее проекцией на плоскость нулевого уровня - угол наклона прямой α.
Слайд 8Проекции с числовыми отметками (проецирование прямых)
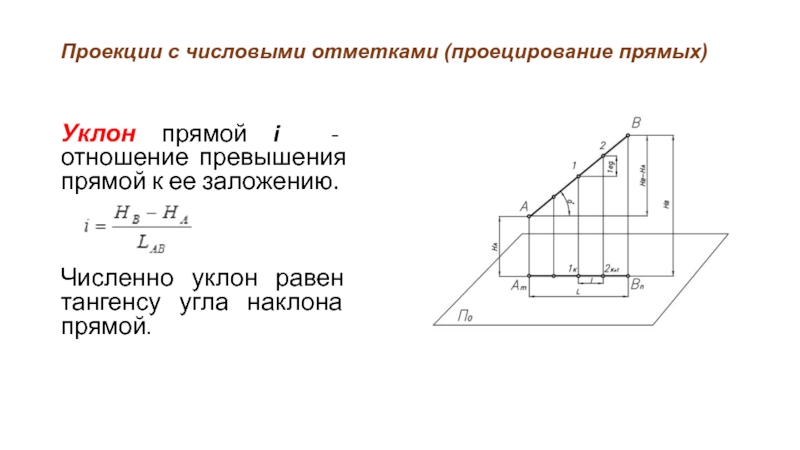
Уклон прямой i - отношение превышения
прямой к ее заложению.
Численно уклон равен тангенсу угла наклона прямой.
Численно уклон равен тангенсу угла наклона прямой.
Слайд 9Проекции с числовыми отметками (проецирование прямых)
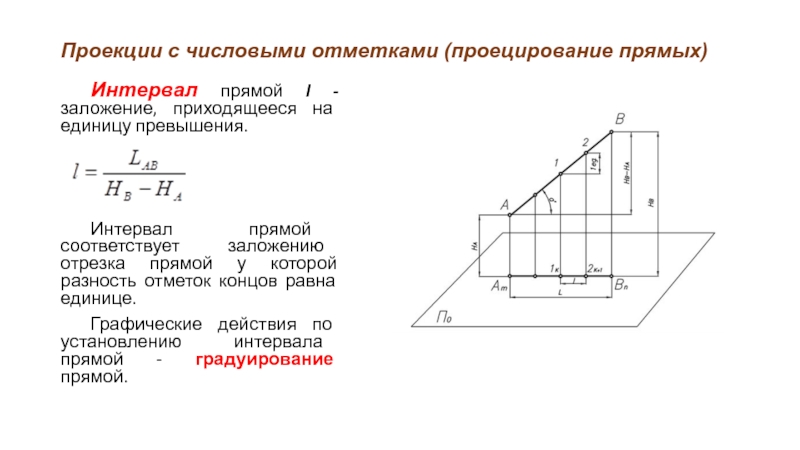
Интервал прямой l - заложение, приходящееся
на единицу превышения.
Интервал прямой соответствует заложению отрезка прямой у которой разность отметок концов равна единице.
Графические действия по установлению интервала прямой - градуирование прямой.
Интервал прямой соответствует заложению отрезка прямой у которой разность отметок концов равна единице.
Графические действия по установлению интервала прямой - градуирование прямой.
Слайд 10Проекции с числовыми отметками (проецирование прямых)
Интервал и уклон являются обратными величинами.
l=1/i,
i=1/l
Слайд 11Проекции с числовыми отметками (проецирование прямых)
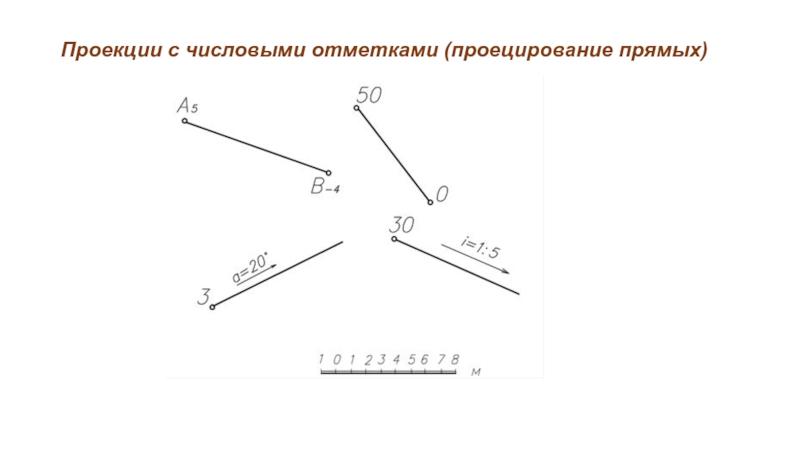
Прямую в проекциях с числовыми отметками
задают:
проекциями двух точек с отметками;
проекцией одной точки и направлением спуска с указанием уклона или интервала;
проекцией одной точки и направлением спуска с указанием угла наклона прямой к плоскости нулевого уровня.
проекциями двух точек с отметками;
проекцией одной точки и направлением спуска с указанием уклона или интервала;
проекцией одной точки и направлением спуска с указанием угла наклона прямой к плоскости нулевого уровня.
Слайд 13Проекции с числовыми отметками (проецирование прямых)
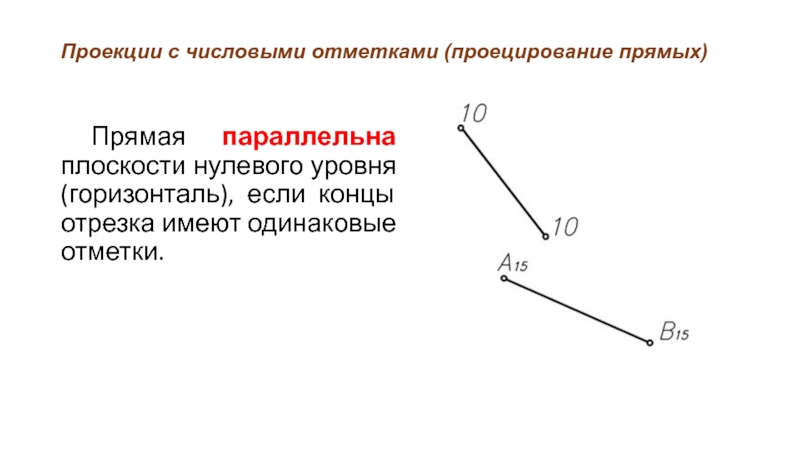
Прямая параллельна плоскости нулевого уровня (горизонталь),
если концы отрезка имеют одинаковые отметки.
Слайд 14Проекции с числовыми отметками (проецирование прямых)
Если проекция прямой точка, то прямая
перпендикулярна плоскости нулевого уровня.
Слайд 15Проекции с числовыми отметками (проецирование прямых)
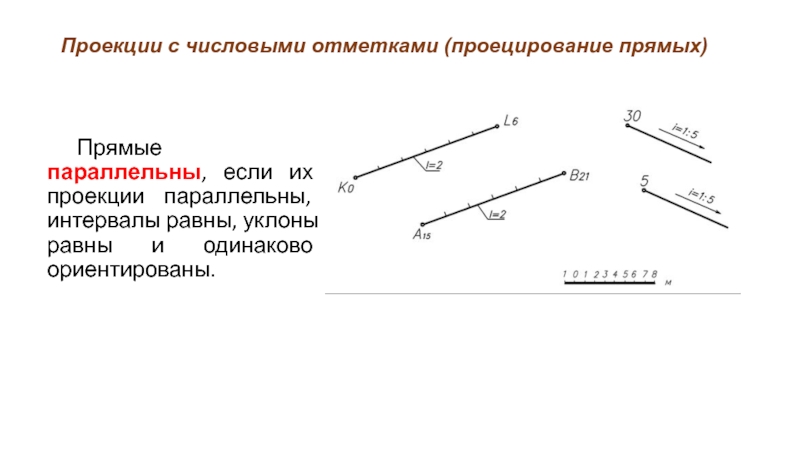
Прямые параллельны, если их проекции параллельны,
интервалы равны, уклоны равны и одинаково ориентированы.
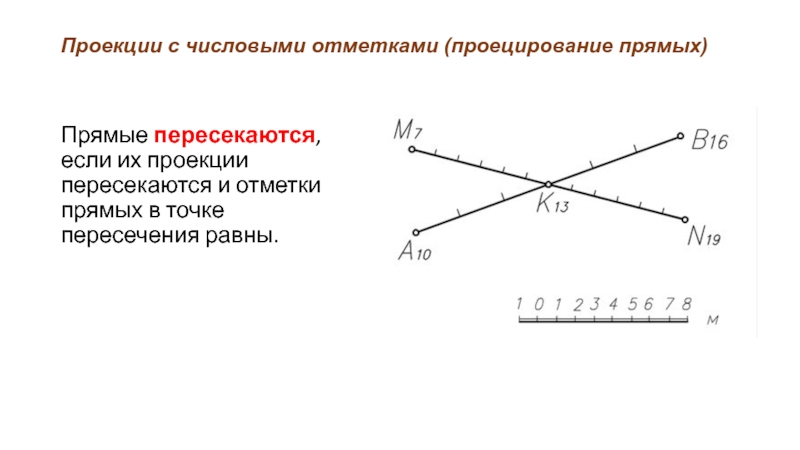
Слайд 16Проекции с числовыми отметками (проецирование прямых)
Прямые пересекаются, если их проекции пересекаются
и отметки прямых в точке пересечения равны.
Слайд 17Проекции с числовыми отметками (проецирование прямых)
Если проекции прямых не удовлетворяют приведенным
выше требованиям – прямые скрещиваются.
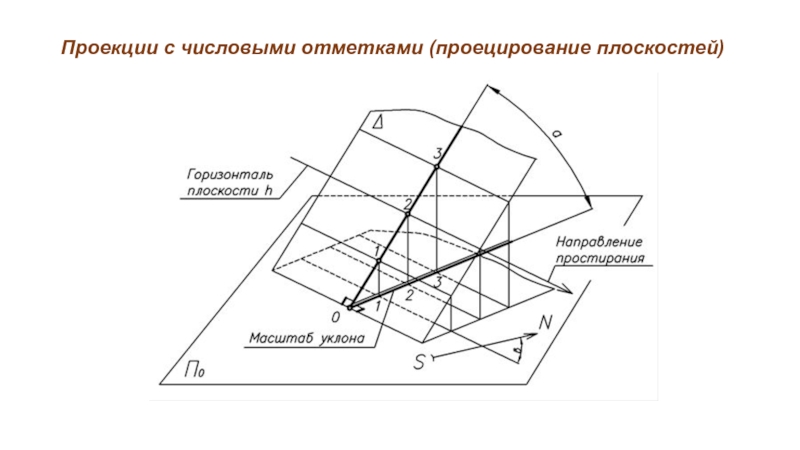
Слайд 18Проекции с числовыми отметками (проецирование плоскостей)
Масштаб уклона - градуированная проекция линии
ската плоскости (линию наибольшего наклона плоскости к горизонтальной плоскости проекций), перпендикулярной горизонталям плоскости.
Масштаб уклона обозначают двойной линией аналогично линейному масштабу с указанием высотных отметок и обозначением заглавной буквой греческого алфавита.
Масштаб уклона обозначают двойной линией аналогично линейному масштабу с указанием высотных отметок и обозначением заглавной буквой греческого алфавита.
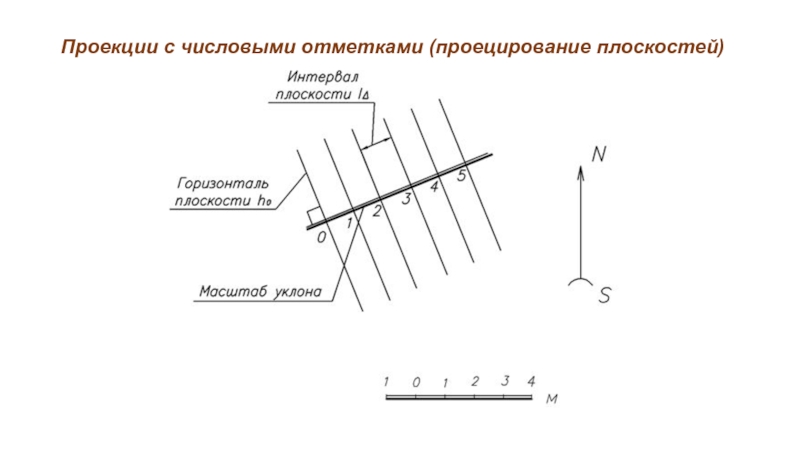
Слайд 19Проекции с числовыми отметками (проецирование плоскостей)
Интервал плоскости - расстояние между проекциями
смежных горизонталей.
Интервал плоскости равен интервалу линии наибольшего ската этой плоскости.
Интервал плоскости обратно пропорционален уклону плоскости, равному уклону линии ската плоскости.
Интервал плоскости равен интервалу линии наибольшего ската этой плоскости.
Интервал плоскости обратно пропорционален уклону плоскости, равному уклону линии ската плоскости.
Слайд 20Проекции с числовыми отметками (проецирование плоскостей)
Угол αр между линией наибольшего ската
и линией масштаба уклонов - угол наибольшего ската или угол падения плоскости.
Угол βр между проекциями горизонталей и направлением земного меридиана - угол простирания.
Угол простирания βр измеряется по часовой стрелке от северного меридиана до положительного направления простирания. Положительное направление простирания идет вправо от наблюдателя, стоящего лицом в сторону возрастания отметок.
Угол βр между проекциями горизонталей и направлением земного меридиана - угол простирания.
Угол простирания βр измеряется по часовой стрелке от северного меридиана до положительного направления простирания. Положительное направление простирания идет вправо от наблюдателя, стоящего лицом в сторону возрастания отметок.
Слайд 23Проекции с числовыми отметками (проецирование плоскостей)
Плоскость
в проекциях с числовыми отметками
задают:
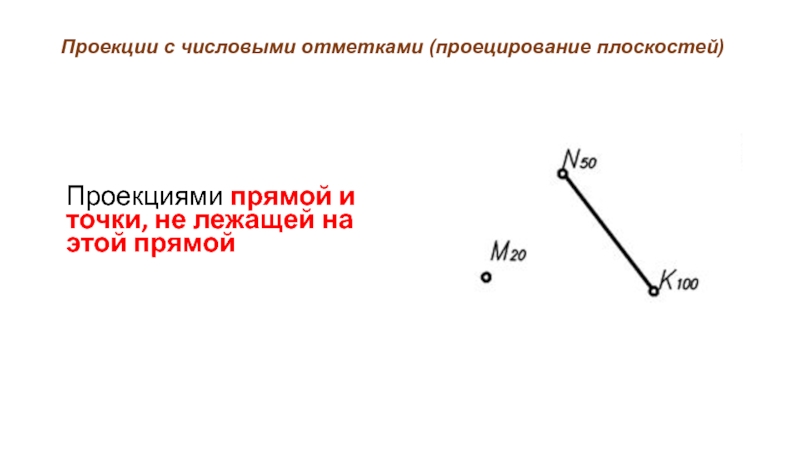
Слайд 25Проекции с числовыми отметками (проецирование плоскостей)
Проекциями прямой и точки, не лежащей
на этой прямой
Слайд 29Проекции с числовыми отметками
Масштабом уклона плоскости (наиболее часто встречающийся и удобный
способ)
Слайд 30Проекции с числовыми отметками (проецирование плоскостей)
Горизонталями плоскости, объединенными тонкой линией, около
которых указывают высотные отметки горизонталей
Слайд 31Проекции с числовыми отметками (проецирование плоскостей)
Горизонталью, уклоном и направлением спуска, которое
обозначают штрихом, направленным в сторону спуска (бергштрихом).
Слайд 32Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
Плоскости параллельны, если
масштабы уклонов взаимно параллельны, интервалы равны и отметки возрастают в одном направлении.
Слайд 33Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
Плоскости пересекаются, если
не выполняется хотя бы одно из требований параллельности плоскостей.
Линию пересечения плоскостей определяют с помощью масштабов уклонов и горизонталей плоскости. Если масштабы уклонов не параллельны, то для определения проекции линии пересечения плоскостей необходимо найти две точки пересечения одноименных горизонталей.
Линию пересечения плоскостей определяют с помощью масштабов уклонов и горизонталей плоскости. Если масштабы уклонов не параллельны, то для определения проекции линии пересечения плоскостей необходимо найти две точки пересечения одноименных горизонталей.
Слайд 35Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
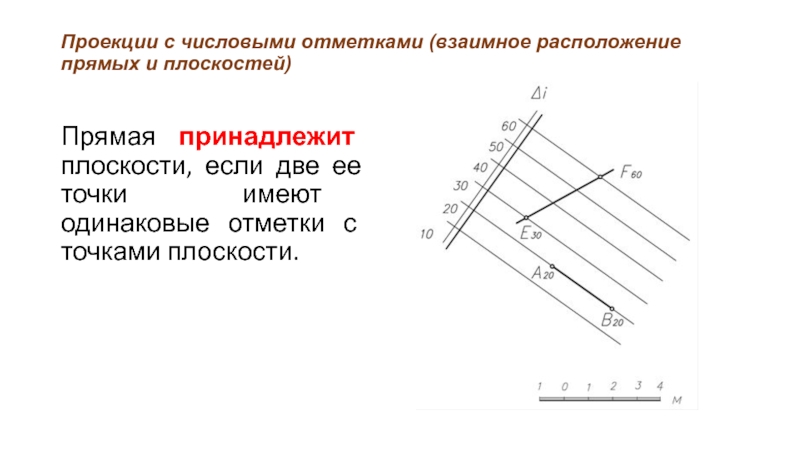
Прямая принадлежит плоскости,
если две ее точки имеют одинаковые отметки с точками плоскости.
Слайд 36Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
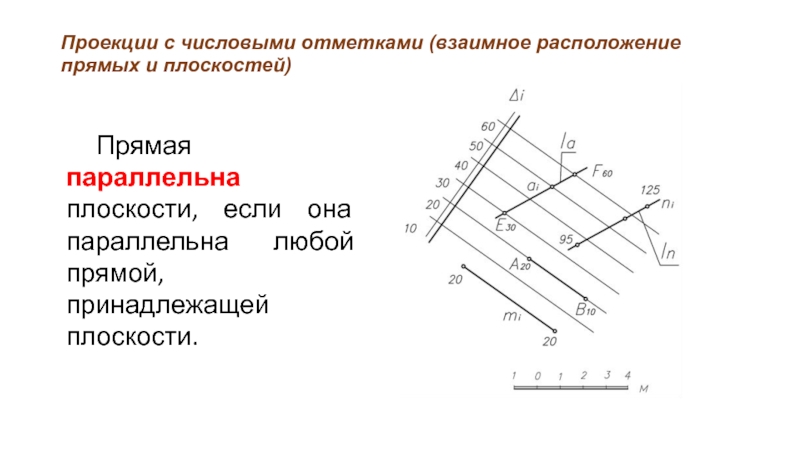
Прямая параллельна плоскости,
если она параллельна любой прямой, принадлежащей плоскости.
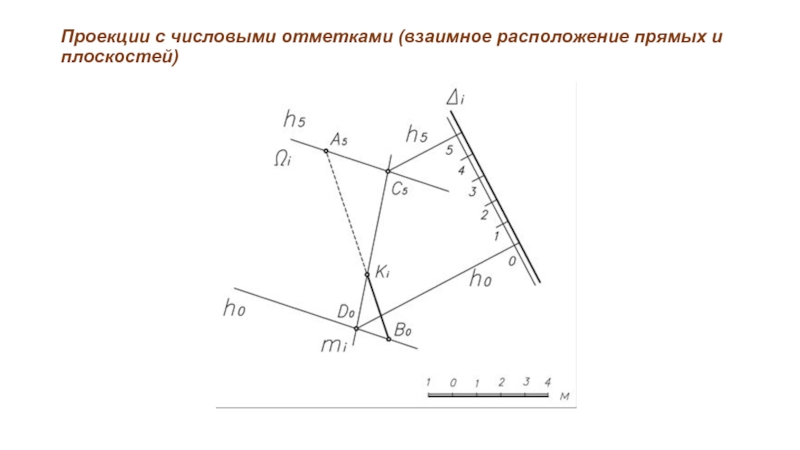
Слайд 37Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
Прямая пересекает плоскость,
если не выполняются условия принадлежности и параллельности.
Построение точки пересечения прямой АВ с плоскостью Δ выполняют по следующему алгоритму:
заключают прямую во вспомогательную плоскость общего положения Ω, для этого через две точки прямой под любым углом проводят две горизонтали, которые и определяют вспомогательную плоскость;
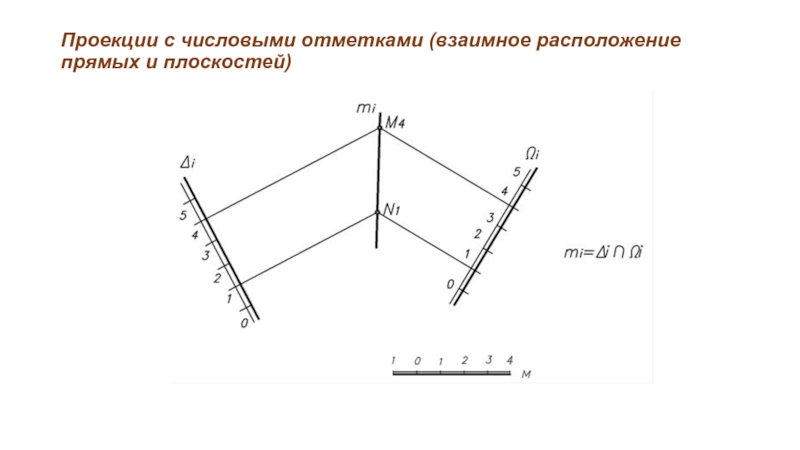
строят прямую линию m пересечения заданной плоскости Δ и вспомогательной плоскости Ω;
точка К пересечения заданной прямой АВ и линии пересечения плоскостей m является точкой пересечения заданной прямой и плоскости;
определяют видимость прямой относительно плоскости.
Построение точки пересечения прямой АВ с плоскостью Δ выполняют по следующему алгоритму:
заключают прямую во вспомогательную плоскость общего положения Ω, для этого через две точки прямой под любым углом проводят две горизонтали, которые и определяют вспомогательную плоскость;
строят прямую линию m пересечения заданной плоскости Δ и вспомогательной плоскости Ω;
точка К пересечения заданной прямой АВ и линии пересечения плоскостей m является точкой пересечения заданной прямой и плоскости;
определяют видимость прямой относительно плоскости.
Слайд 39Проекции с числовыми отметками (взаимное расположение прямых и плоскостей)
Прямая и плоскость
взаимно перпендикулярны, если проекция прямой и масштаб уклона плоскости взаимно параллельны, отметки прямой и плоскости возрастают в противоположных направлениях, интервалы (уклоны) прямой и плоскости обратно пропорциональны
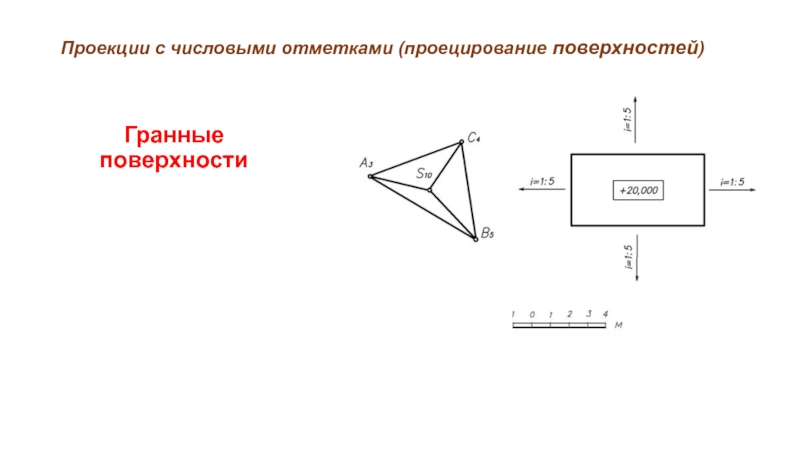
Слайд 40Проекции с числовыми отметками (проецирование поверхностей)
Гранные поверхности в проекциях с числовыми
отметками задают:
проекциями ребер с указанием отметок вершин;
проекцией и отметками одной из граней и уклонами других граней.
Кривые поверхности, поверхности одинакового ската и топографические поверхности задают проекциями горизонталей (линиями сечения поверхности горизонтальными плоскостями уровня), а также проекциями и отметками отдельных характерных точек поверхности.
проекциями ребер с указанием отметок вершин;
проекцией и отметками одной из граней и уклонами других граней.
Кривые поверхности, поверхности одинакового ската и топографические поверхности задают проекциями горизонталей (линиями сечения поверхности горизонтальными плоскостями уровня), а также проекциями и отметками отдельных характерных точек поверхности.
Слайд 41Проекции с числовыми отметками (проецирование поверхностей)
Линией ската поверхности называют линию поверхности,
которая в данной точке наклонена к горизонтальной плоскости под наибольшим углом. Линия ската перпендикулярна горизонтали поверхности, проведенной через эту точку.
Градуированием поверхности называют построение горизонталей поверхности с отметками, выраженными целыми числами и отличающимися на единицу длины.
Градуированием поверхности называют построение горизонталей поверхности с отметками, выраженными целыми числами и отличающимися на единицу длины.
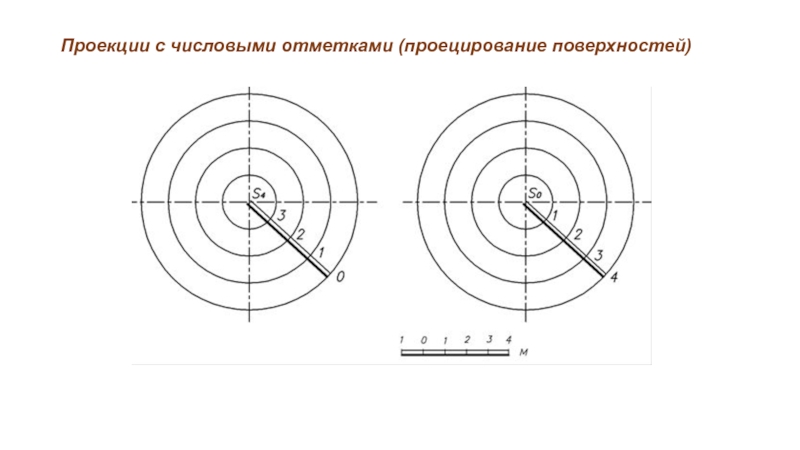
Слайд 43Проекции с числовыми отметками (проецирование поверхностей)
Конические поверхности общего вида в проекциях
с числовыми отметками изображают направляющей горизонталью и вершиной.
Прямой круговой конус изображают рядом концентрических окружностей, эллиптический конус с круговым основанием - эксцентрическими окружностями.
Конус может быть задан проекцией вершины и масштабом уклона (проградуированной линией ската).
Прямой круговой конус изображают рядом концентрических окружностей, эллиптический конус с круговым основанием - эксцентрическими окружностями.
Конус может быть задан проекцией вершины и масштабом уклона (проградуированной линией ската).
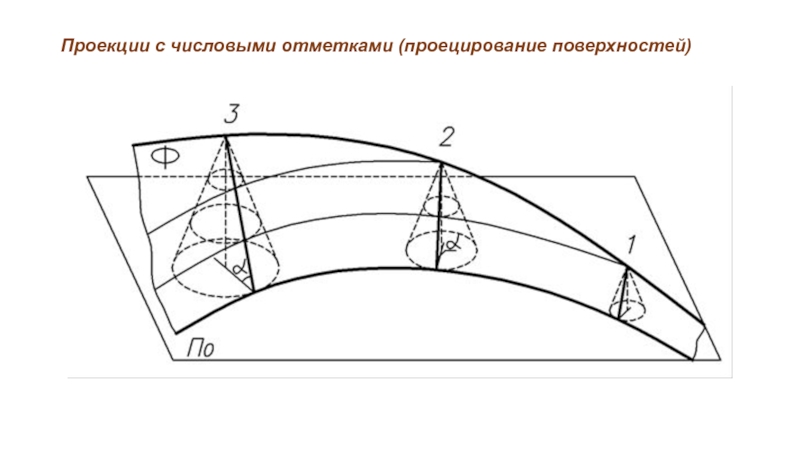
Слайд 45Проекции с числовыми отметками (проецирование поверхностей)
Поверхность одинакового ската - линейчатая поверхность,
представляющая собой огибающую семейства прямых круговых конусов, вершины которых расположены на некоторой пространственной линии (направляющей), а оси перпендикулярны плоскости проекций П0 (плоскости нулевого уровня).
Все образующие этой поверхности составляют с плоскостью нулевого уровня постоянный угол.
Линия ската такой поверхности совпадает с линией касания конуса и соприкасающейся поверхности.
Все образующие этой поверхности составляют с плоскостью нулевого уровня постоянный угол.
Линия ската такой поверхности совпадает с линией касания конуса и соприкасающейся поверхности.
Слайд 47Проекции с числовыми отметками (проецирование поверхностей)
Проекция поверхности одинакового ската строится по
следующему алгоритму:
градуируют проекцию направляющей, найденные точки являются проекциями вершин конусов;
из полученных точек вычерчивают горизонтали конусов в соответствии с заданным интервалом (уклоном);
строят горизонтали поверхности одинакового ската как линии, огибающие семейства окружностей (горизонталей конусов), имеющих одну и ту же отметку.
Расстояние между двумя проекциями смежных горизонталей в направлении общей нормали к ним везде одинаково.
градуируют проекцию направляющей, найденные точки являются проекциями вершин конусов;
из полученных точек вычерчивают горизонтали конусов в соответствии с заданным интервалом (уклоном);
строят горизонтали поверхности одинакового ската как линии, огибающие семейства окружностей (горизонталей конусов), имеющих одну и ту же отметку.
Расстояние между двумя проекциями смежных горизонталей в направлении общей нормали к ним везде одинаково.
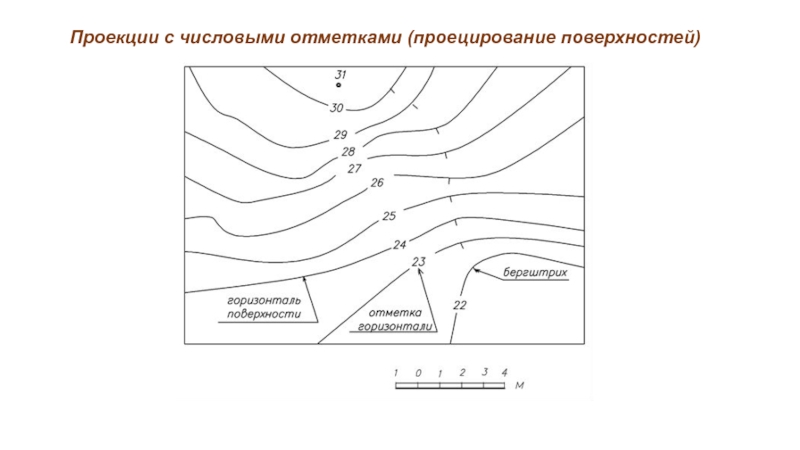
Слайд 49Проекции с числовыми отметками (проецирование поверхностей)
Топографическая поверхность - поверхность, строение которой
не подчинено строгому математическому описанию. Топографическую поверхность задают дискретным каркасом – горизонталями или профилем, а также отдельными точками.
Проекции горизонталей на плоскость нулевого уровня (горизонтальную плоскость проекций) образуют план топографической поверхности.
При изображении топографических поверхностей кроме отметок используют бергштихи, показывающие направление ската поверхности. Их проводят от горизонталей с большими отметками в сторону горизонталей с меньшими отметками.
Проекции горизонталей на плоскость нулевого уровня (горизонтальную плоскость проекций) образуют план топографической поверхности.
При изображении топографических поверхностей кроме отметок используют бергштихи, показывающие направление ската поверхности. Их проводят от горизонталей с большими отметками в сторону горизонталей с меньшими отметками.
Слайд 51Проекции с числовыми отметками (проецирование поверхностей)
Основные параметры топографической поверхности:
Высота сечения Δh
- расстояние между соседними по высоте горизонталями.
Интервал горизонталей l - отрезок, равный расстоянию между двумя соседними горизонталями на плане.
Линия ската топографической поверхности - линия, которая в данной точке поверхности имеет наибольший уклон.
Линия равного уклона топографической поверхности - линия, имеющая одинаковый интервал на всем протяжении.
Интервал горизонталей l - отрезок, равный расстоянию между двумя соседними горизонталями на плане.
Линия ската топографической поверхности - линия, которая в данной точке поверхности имеет наибольший уклон.
Линия равного уклона топографической поверхности - линия, имеющая одинаковый интервал на всем протяжении.
Слайд 52Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Линия сечения поверхности
плоскостью в проекциях с числовыми отметками строится по точкам пересечения горизонталей плоскости и поверхности, имеющих одинаковые отметки.
Слайд 53Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
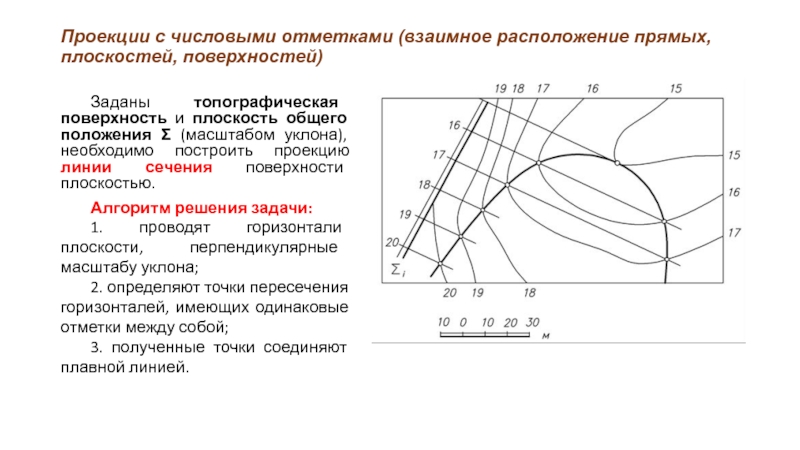
Заданы топографическая поверхность
и плоскость общего положения Σ (масштабом уклона), необходимо построить проекцию линии сечения поверхности плоскостью.
Алгоритм решения задачи:
1. проводят горизонтали плоскости, перпендикулярные масштабу уклона;
2. определяют точки пересечения горизонталей, имеющих одинаковые отметки между собой;
3. полученные точки соединяют плавной линией.
Алгоритм решения задачи:
1. проводят горизонтали плоскости, перпендикулярные масштабу уклона;
2. определяют точки пересечения горизонталей, имеющих одинаковые отметки между собой;
3. полученные точки соединяют плавной линией.
Слайд 54Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Линия сечения поверхности
плоскостью, параллельной плоскости нулевого уровня (плоскостью уровня) – горизонталь поверхности (все точки кривой имеют одинаковую отметку).
Слайд 55Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Линию сечения топографической
поверхности плоскостью перпендикулярной плоскости нулевого уровня называют профилем топографической поверхности.
Алгоритм построения профиля топографической поверхности:
1. задается направление профиля (прямая линия АВ);
2. в точках пересечения прямой с горизонталями поверхности восстанавливают перпендикуляры к прямой;
3. на перпендикулярах откладывают отметки точек в масштабе чертежа и соединяют их плавной линией.
Алгоритм построения профиля топографической поверхности:
1. задается направление профиля (прямая линия АВ);
2. в точках пересечения прямой с горизонталями поверхности восстанавливают перпендикуляры к прямой;
3. на перпендикулярах откладывают отметки точек в масштабе чертежа и соединяют их плавной линией.
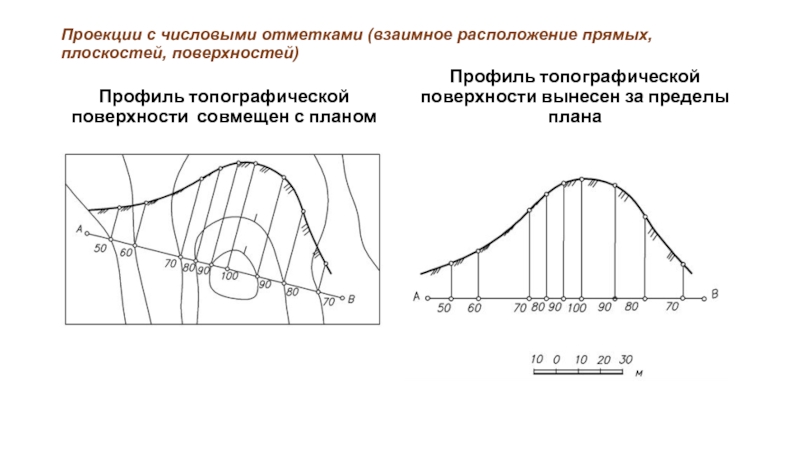
Слайд 56Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Профиль топографической поверхности
совмещен с планом
Профиль топографической поверхности вынесен за пределы плана
Слайд 57Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Построение проекций точек
пересечения прямой с поверхностью
Алгоритм определения точек пересечения прямой с поверхностью в проекциях с числовыми отметками:
прямую заключают во вспомогательную секущую плоскость (в качестве вспомогательных плоскостей выбирают как плоскости, перпендикулярные плоскости нулевого уровня, так и плоскости общего положения);
строят линию сечения поверхности плоскостью;
определяют точки пересечения заданной прямой и линии сечения;
определяют видимость прямой относительно поверхности.
Алгоритм определения точек пересечения прямой с поверхностью в проекциях с числовыми отметками:
прямую заключают во вспомогательную секущую плоскость (в качестве вспомогательных плоскостей выбирают как плоскости, перпендикулярные плоскости нулевого уровня, так и плоскости общего положения);
строят линию сечения поверхности плоскостью;
определяют точки пересечения заданной прямой и линии сечения;
определяют видимость прямой относительно поверхности.
Слайд 58Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
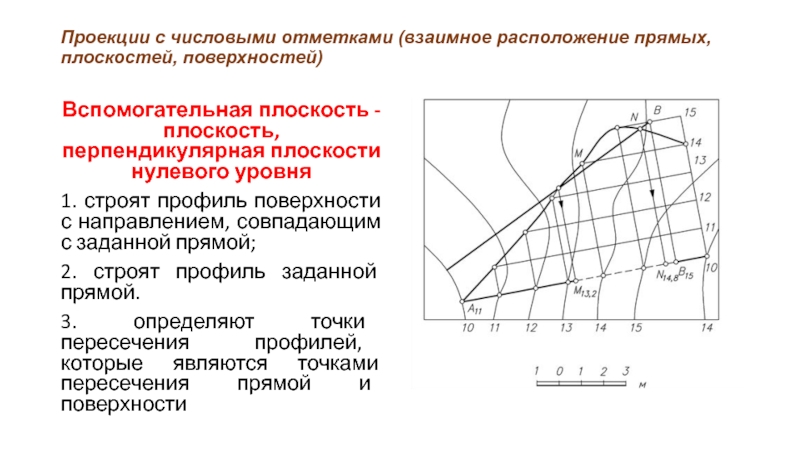
Вспомогательная плоскость -
плоскость, перпендикулярная плоскости нулевого уровня
1. строят профиль поверхности с направлением, совпадающим с заданной прямой;
2. строят профиль заданной прямой.
3. определяют точки пересечения профилей, которые являются точками пересечения прямой и поверхности
1. строят профиль поверхности с направлением, совпадающим с заданной прямой;
2. строят профиль заданной прямой.
3. определяют точки пересечения профилей, которые являются точками пересечения прямой и поверхности
Слайд 59Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
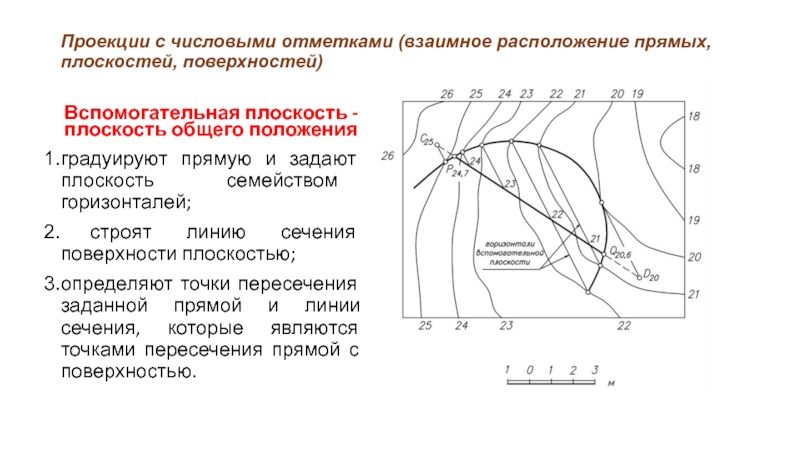
Вспомогательная плоскость -
плоскость общего положения
градуируют прямую и задают плоскость семейством горизонталей;
строят линию сечения поверхности плоскостью;
определяют точки пересечения заданной прямой и линии сечения, которые являются точками пересечения прямой с поверхностью.
градуируют прямую и задают плоскость семейством горизонталей;
строят линию сечения поверхности плоскостью;
определяют точки пересечения заданной прямой и линии сечения, которые являются точками пересечения прямой с поверхностью.
Слайд 60Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Проекцию линии пересечения
поверхностей в проекциях с числовыми отметками строят согласно следующему алгоритму:
проводят проекции горизонталей заданных поверхностей;
определяют точки пересечения горизонталей, имеющих одинаковые отметки;
полученные точки соединяют в линию, которая и будет линией пересечения заданных поверхностей.
проводят проекции горизонталей заданных поверхностей;
определяют точки пересечения горизонталей, имеющих одинаковые отметки;
полученные точки соединяют в линию, которая и будет линией пересечения заданных поверхностей.
Слайд 61Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
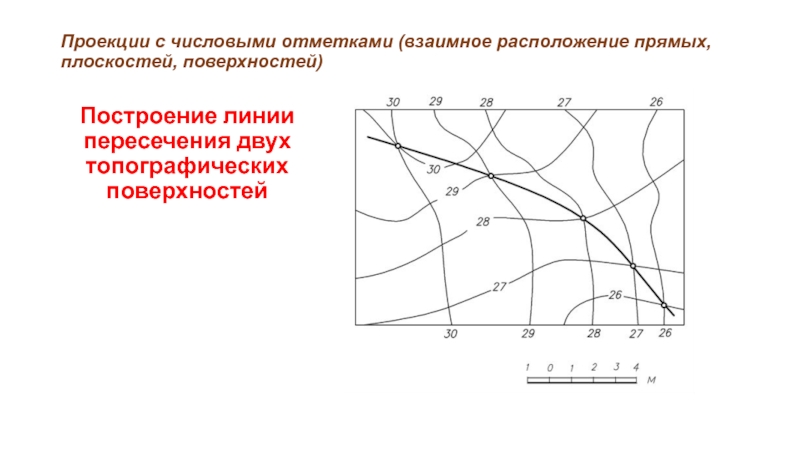
Построение линии пересечения
двух топографических поверхностей
Слайд 62Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Построение линии пересечения
конической и топографической поверхностей
m1 – горизонталь, qi – образующая конической поверхности;
n1 – горизонталь топографической поверхности;
М1 – точка пересечения одноименных горизонталей;
Кi - промежуточная точка линии пересечения
m1 – горизонталь, qi – образующая конической поверхности;
n1 – горизонталь топографической поверхности;
М1 – точка пересечения одноименных горизонталей;
Кi - промежуточная точка линии пересечения
Слайд 63Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
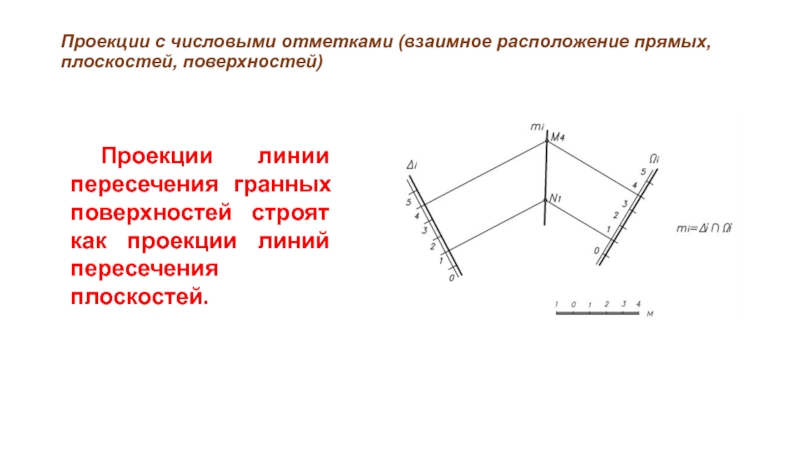
Проекции линии пересечения
гранных поверхностей строят как проекции линий пересечения плоскостей.
Слайд 64Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Если одна из
поверхностей – гранная, а вторая поверхность является кривой, поверхностью одинакового ската или топографической, то проекцию линии пересечения поверхностей строят как проекцию линии сечения поверхности плоскостью.
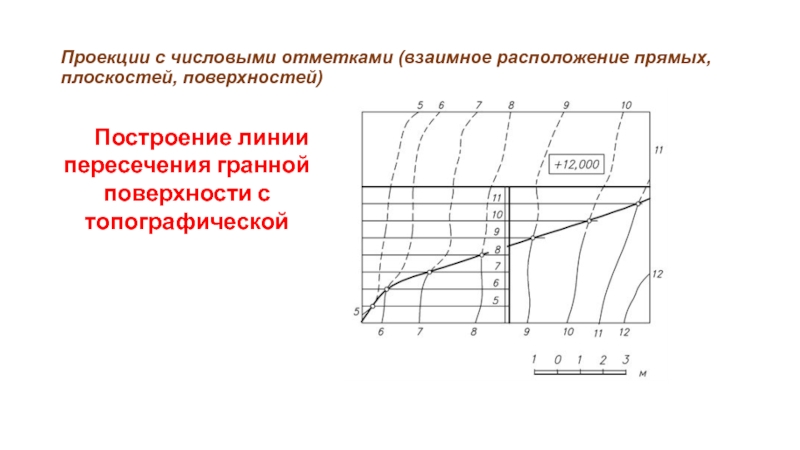
Слайд 65Проекции с числовыми отметками (взаимное расположение прямых, плоскостей, поверхностей)
Построение линии пересечения
гранной поверхности с топографической