- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Примеры задач линейного программирования презентация
Содержание
- 1. Примеры задач линейного программирования
- 2. Для изготовления двух видов продукции Р1
- 3. Решение Введем переменные Задача
- 4. Решение Ограничения Задача об
- 5. Экономико-математическая модель (задача линейного программирования) Задача об использовании ресурсов
- 6. Экономико-математическая модель (коротко)
- 7. В дневной рацион питания цыплят включают
- 8. Решение Введем переменные Задача
- 9. Решение Ограничения Задача составления
- 10. Экономико-математическая модель (задача линейного программирования) Задача составления рациона
- 11. Поясним термин линейное программирование линейное означает:
- 12. Общий вид задачи линейного программирования Целевая функция при ограничениях
- 13. Общий вид задачи линейного программирования Краткая форма
- 14. Каноническая задача ЛП В канонической задаче:
- 15. В канонической задаче: 1) Целевая функция
- 16. В канонической задаче: 1) Целевая функция
- 17. В канонической задаче: 1) Целевая функция
- 18. Литература Шикин Е.В., Шикина Г.Е. Исследование операций.
Слайд 2
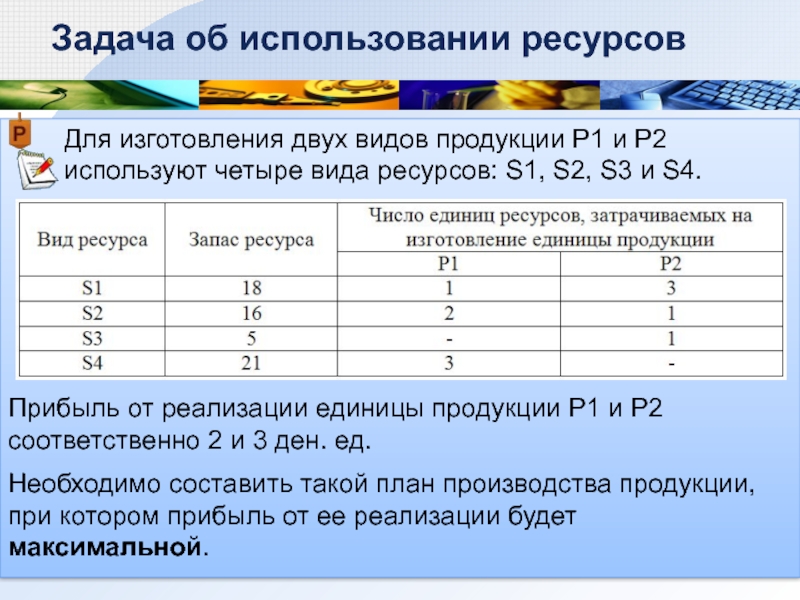
Для изготовления двух видов продукции Р1 и Р2 используют четыре вида
Задача об использовании ресурсов
Прибыль от реализации единицы продукции Р1 и Р2 соответственно 2 и 3 ден. ед.
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Слайд 3
Решение
Введем переменные
Задача об использовании ресурсов
Х1 – число единиц продукции Р1,
Х2 – число единиц продукции Р2, запланированных к производству
Прибыль:
F = 2*X1+3*X2
Цель:
F → max
Слайд 4
Решение
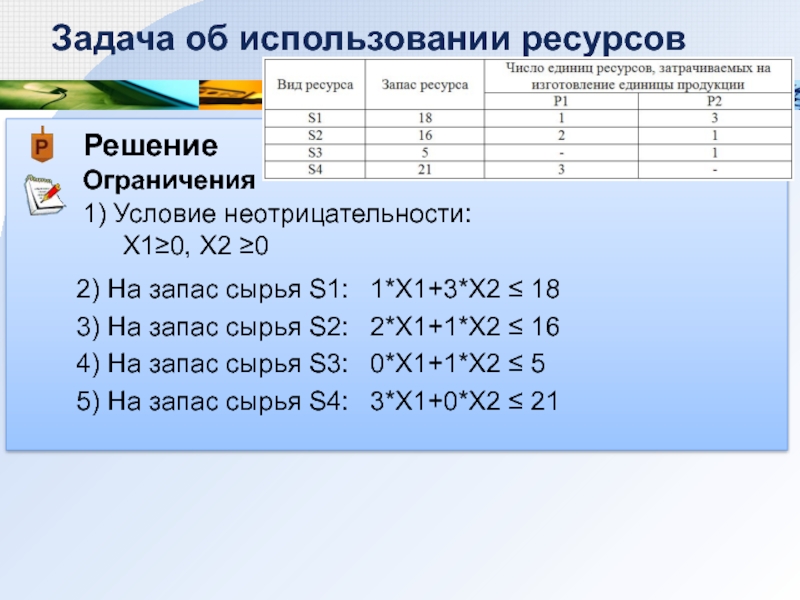
Ограничения
Задача об использовании ресурсов
1) Условие неотрицательности:
Х1≥0, Х2 ≥0
2) На запас
1*X1+3*X2 ≤ 18
3) На запас сырья S2:
4) На запас сырья S3:
5) На запас сырья S4:
2*X1+1*X2 ≤ 16
0*X1+1*X2 ≤ 5
3*X1+0*X2 ≤ 21
Слайд 5
Экономико-математическая модель
(задача линейного программирования)
Задача об использовании ресурсов
Слайд 7
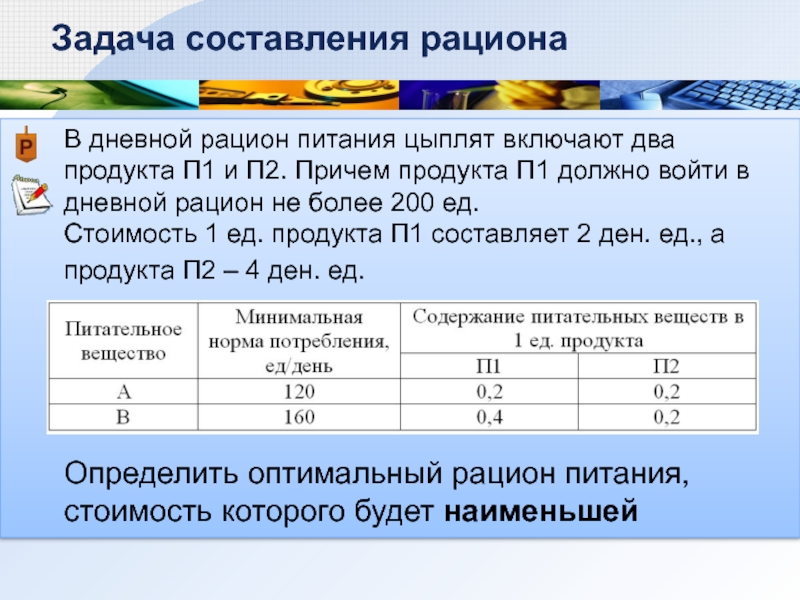
В дневной рацион питания цыплят включают два продукта П1 и П2.
Стоимость 1 ед. продукта П1 составляет 2 ден. ед., а продукта П2 – 4 ден. ед.
Задача составления рациона
Определить оптимальный рацион питания, стоимость которого будет наименьшей
Слайд 8
Решение
Введем переменные
Задача составления рациона
Х1 – число единиц продукта П1, входящего
Х2 – число единиц продукта П2, входящего в дневной рацион
Стоимость дневного рациона :
F = 2*X1+4*X2
Цель:
F → min
Слайд 9
Решение
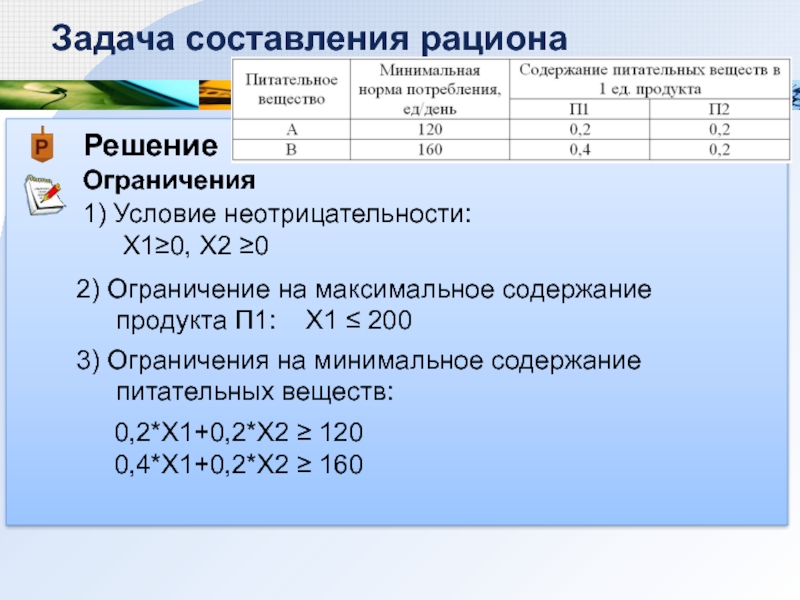
Ограничения
Задача составления рациона
1) Условие неотрицательности:
Х1≥0, Х2 ≥0
2) Ограничение на максимальное
0,2*X1+0,2*X2 ≥ 120
0,4*X1+0,2*X2 ≥ 160
3) Ограничения на минимальное содержание питательных веществ:
Слайд 10
Экономико-математическая модель
(задача линейного программирования)
Задача составления рациона
Слайд 11Поясним термин линейное программирование
линейное означает: ищется экстремальное значение (min или max)
программирование в данном словосочетании имеет смысл планирования
Слайд 14Каноническая задача ЛП
В канонической задаче:
1) Целевая функция → max
2) Все ограничения
3) Все переменные неотрицательны
Слайд 15
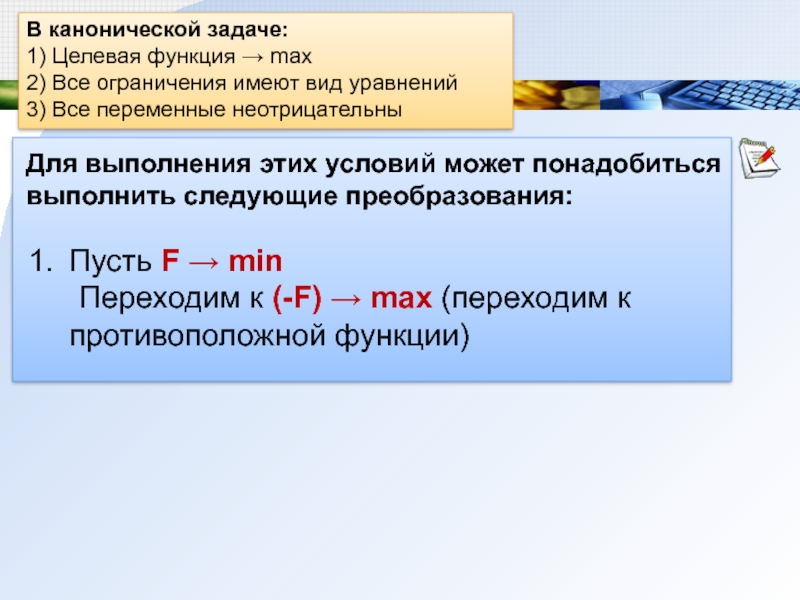
В канонической задаче:
1) Целевая функция → max
2) Все ограничения имеют вид
3) Все переменные неотрицательны
Для выполнения этих условий может понадобиться выполнить следующие преобразования:
Пусть F → min
Переходим к (-F) → max (переходим к противоположной функции)
Слайд 16
В канонической задаче:
1) Целевая функция → max
2) Все ограничения имеют вид
3) Все переменные неотрицательны
Для выполнения этих условий может понадобиться выполнить следующие преобразования:
2. Пусть дано ограничение неравенство
a1x1+a2x2≥b
Вводим новую переменную х3≥0:
a1x1+a2x2-х3 = b
Слайд 17
В канонической задаче:
1) Целевая функция → max
2) Все ограничения имеют вид
3) Все переменные неотрицательны
Для выполнения этих условий может понадобиться выполнить следующие преобразования:
3. Пусть xi ≤ 0
Вводим новые переменные хj≥0, хk≥0 :
xi=xj-хk
Таким образом, задача линейного программирования (ЗЛП) в любом виде может быть преобразована к канонической форме
Слайд 18Литература
Шикин Е.В., Шикина Г.Е. Исследование операций. - М.: ТК Велби, 2006.
Кремер Н.Ш., Путко Б.А. Исследование операций в экономике. - М.: ЮНИТИ, 2003. - 407 с.
Красс М.С., Чупрынов Б.П. Математика для экономистов. - СПб.: Питер, 2005. - 464 с.