ФОРМА ЗАПИСИ ЗАДАЧИ
БАЗИСНАЯ ФОРМА ЗАДАЧИ
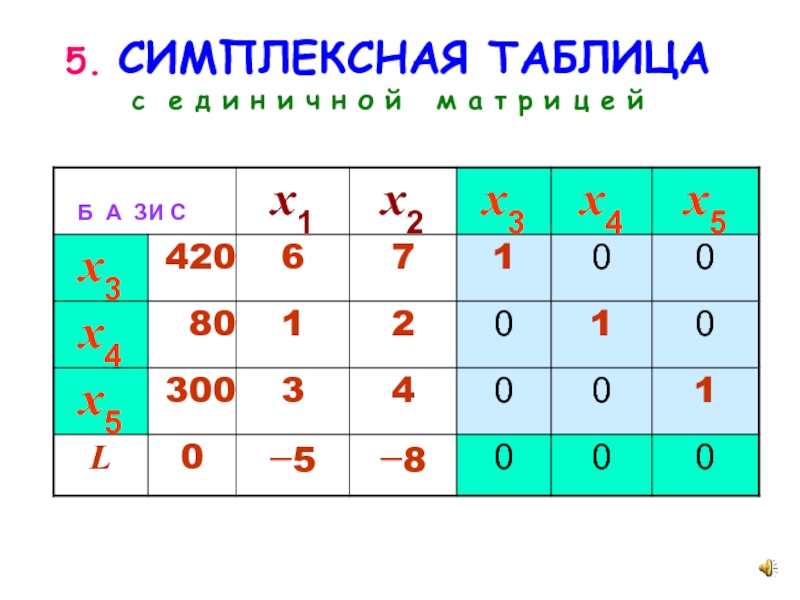
СИМПЛЕКСНАЯ ТАБЛИЦА
ОЦЕНКИ НЕБАЗИСНЫХ ПЕРЕМЕННЫХ
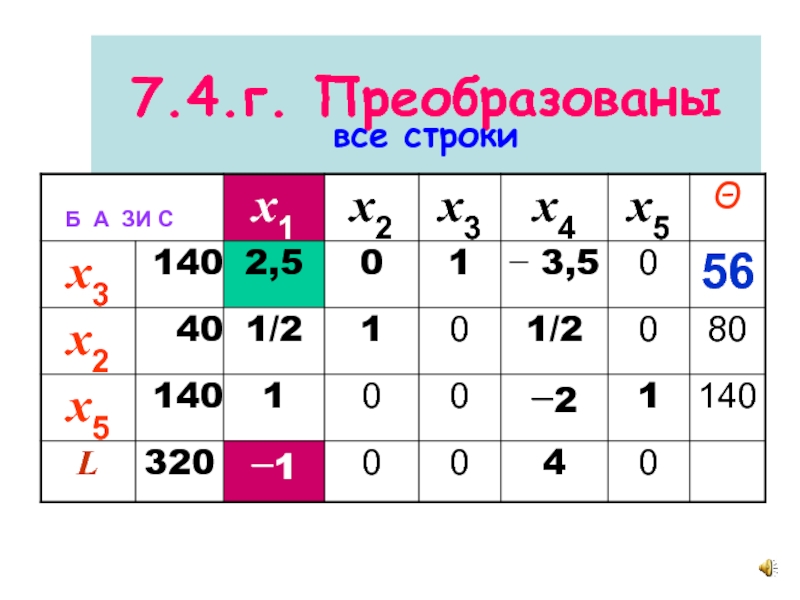
ПРЕОБРАЗОВАНИЕ СИМПЛЕКСНОЙ ТАБЛИЦЫ
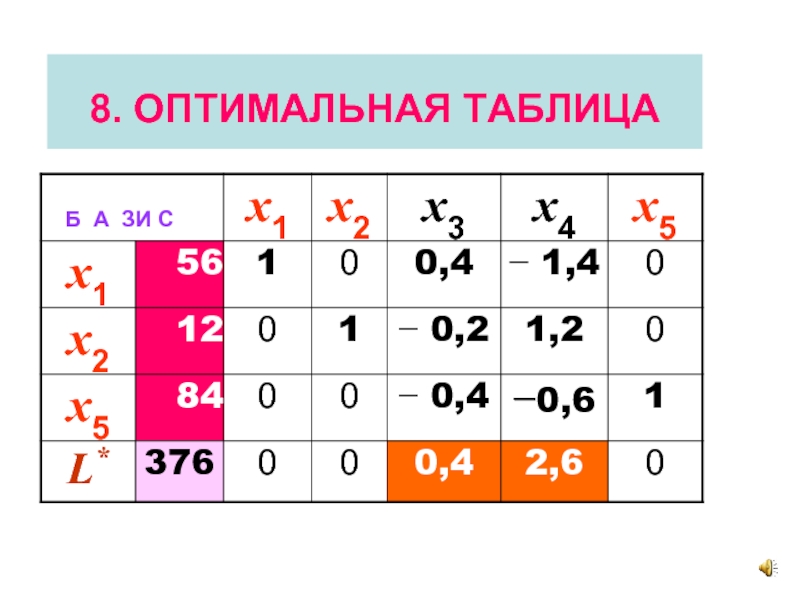
ОПТИМАЛЬНАЯ ТАБЛИЦА
АНАЛИЗ КОНЕЧНОЙ ТАБЛИЦЫ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симплексный метод решения задачи ЛП презентация
Содержание
- 1. Симплексный метод решения задачи ЛП
- 2. 1. Пример исходной задачи ЛП
- 3. 2. Каноническая форма задачи ЛП СТАНДАРТНАЯ
- 4. Приведение к стандартному виду ограничения
- 5. 3. Матричная форма записи задачи
- 6. 5. БАЗИСНАЯ
- 7. СИМПЛЕКСНОЕ ОТНОШЕНИЕ ДЛЯ НОВОЙ БАЗИСНОЙ ПЕРЕМЕННОЙ x2
- 8. Решение разрешающего уравнения относительно x2
- 9. 5. СИМПЛЕКСНАЯ ТАБЛИЦА с е д и
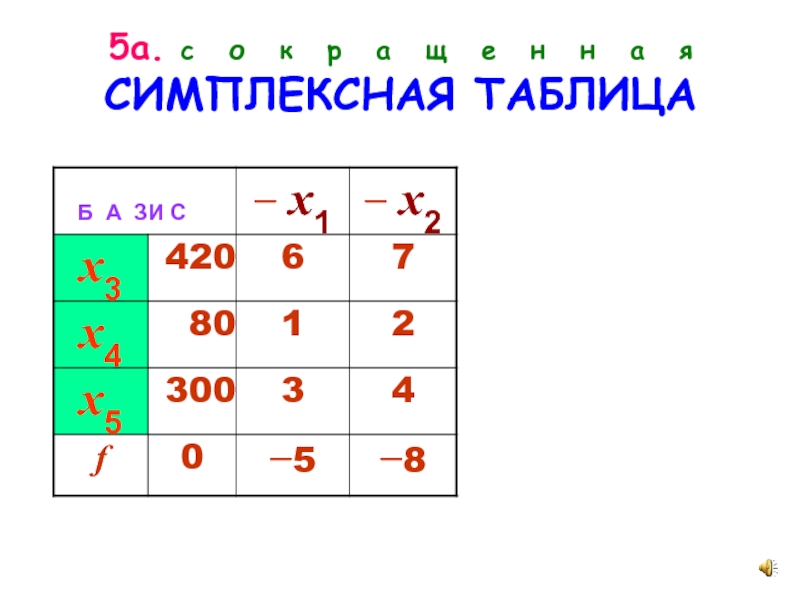
- 10. 5а. с о к
- 11. 6. ОЦЕНКИ НЕБАЗИСНЫХ ПЕРЕМЕННЫХ Оценка
- 12. Небазисная переменная, оценка которой положительна, называется перспективной
- 13. Если текущий опорный план содержит перспективные переменные,
- 14. 7.1. Преобразование СИМПЛЕКСНОЙ
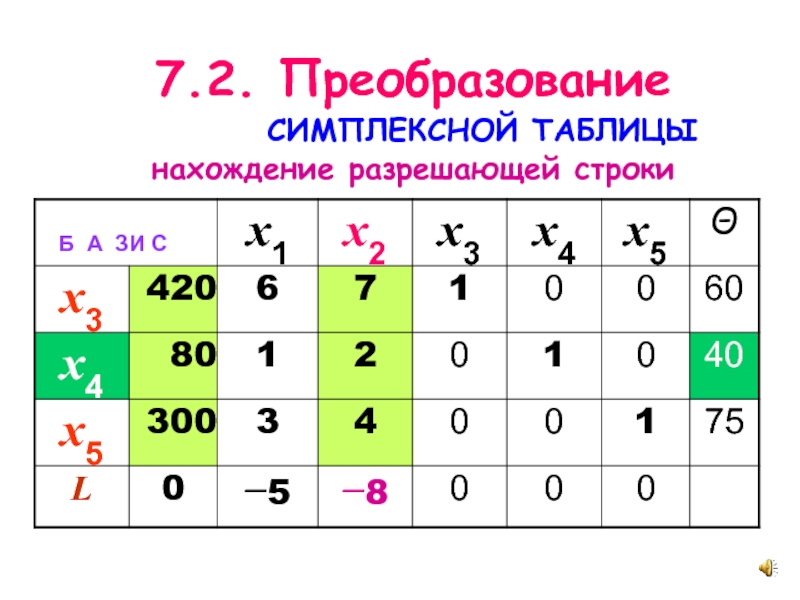
- 15. 7.2. Преобразование СИМПЛЕКСНОЙ ТАБЛИЦЫ нахождение разрешающей строки
- 16. Величина симплексного отношения указывает максимально возможное значение
- 17. Признак неограниченности критерия Если получена очередная таблица,
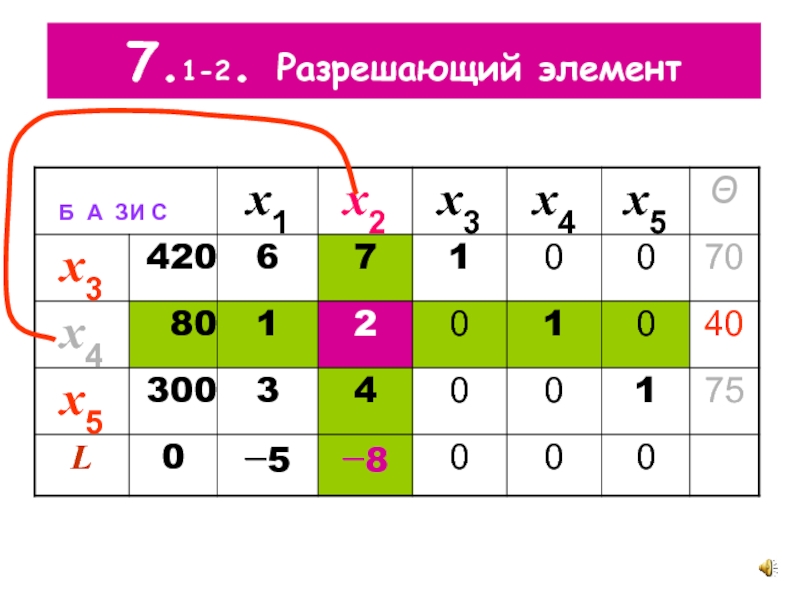
- 18. 7.1-2. Разрешающий элемент
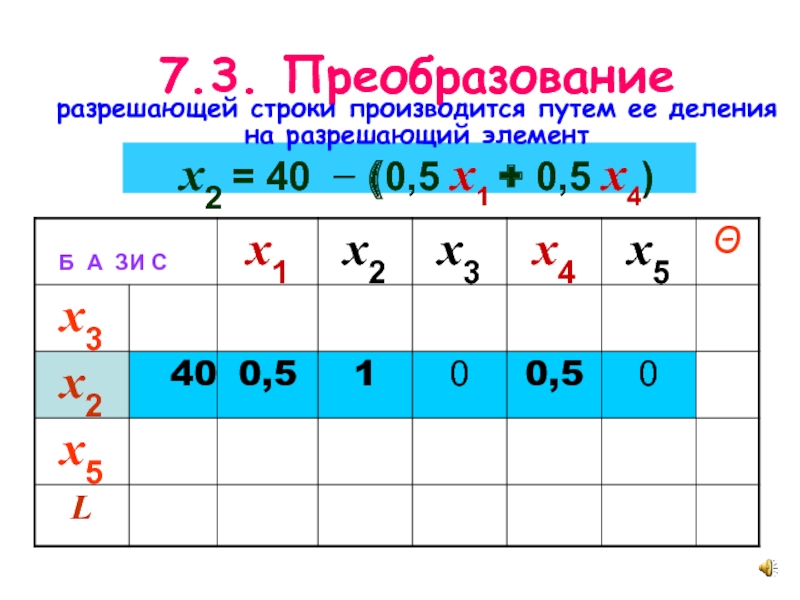
- 19. 7.3. Преобразование разрешающей строки производится
- 20. 7.4а. Преобразование остальных строк Из
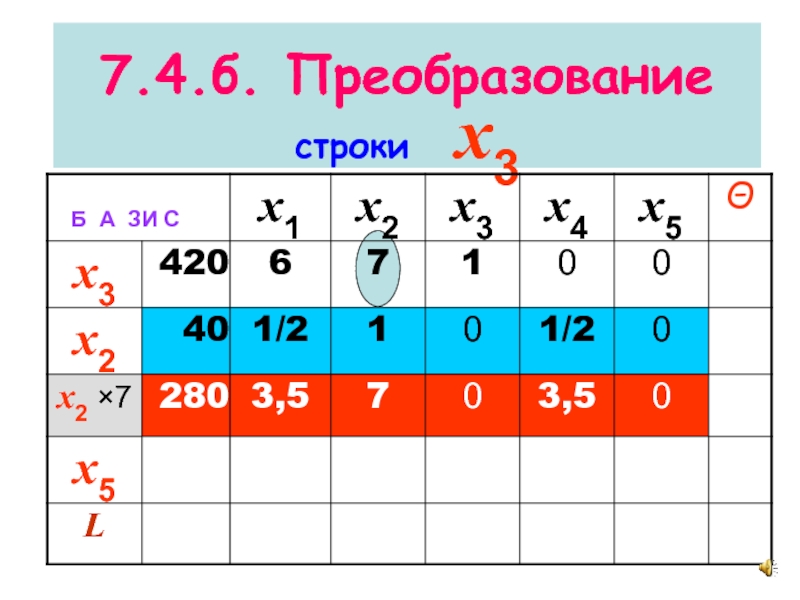
- 21. 7.4.б. Преобразование строки x3
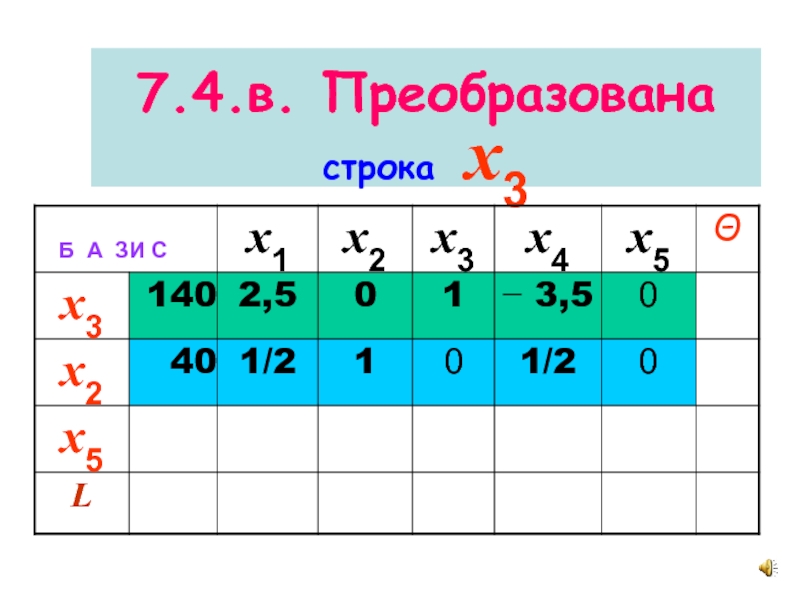
- 22. 7.4.в. Преобразована строка x3
- 23. 7.4.г. Преобразованы все строки
- 24. 8. ОПТИМАЛЬНАЯ ТАБЛИЦА
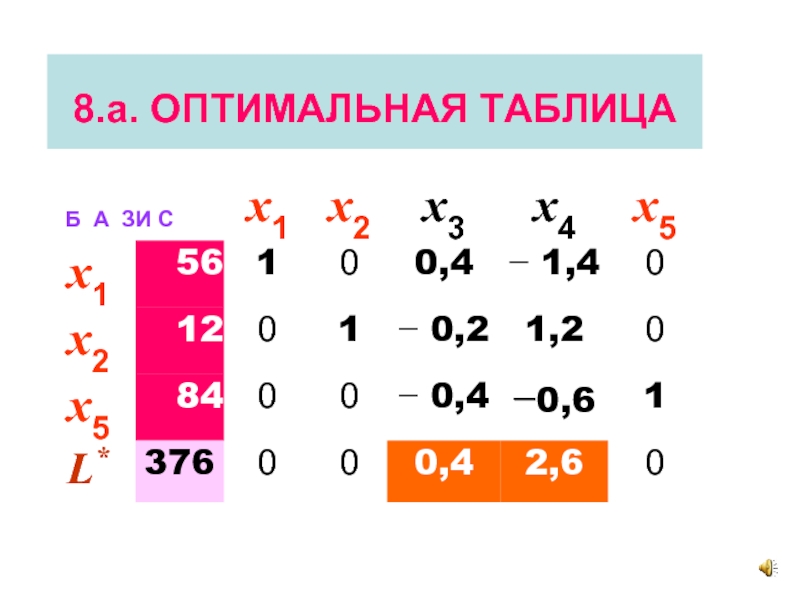
- 25. 8.а. ОПТИМАЛЬНАЯ ТАБЛИЦА
- 26. 8.а. ОПТИМАЛЬНАЯ ТАБЛИЦА
- 27. Базисная форма
- 28. Базисная форма
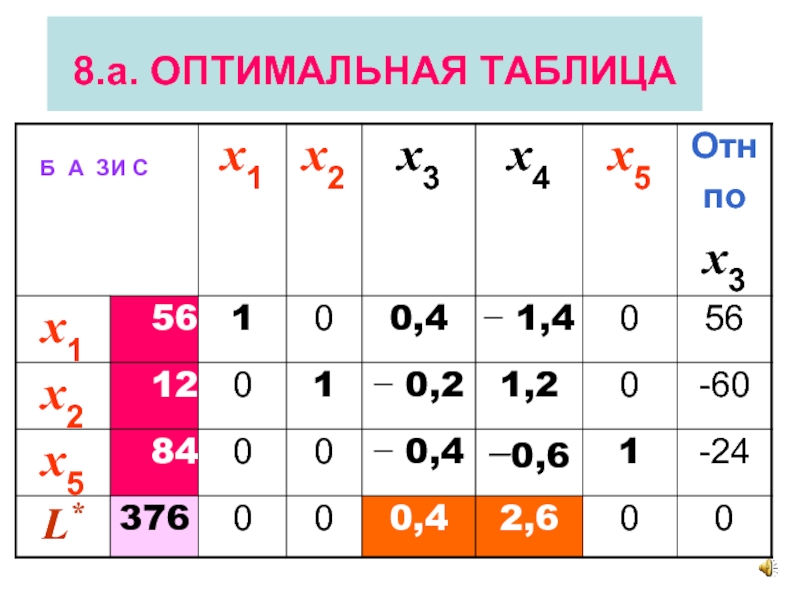
- 29. 8.а. ОПТИМАЛЬНАЯ ТАБЛИЦА
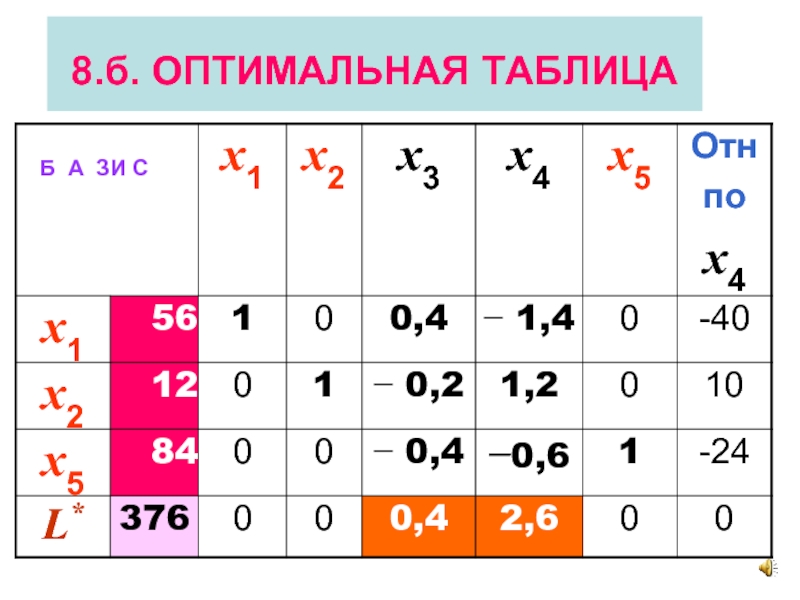
- 30. 8.б. ОПТИМАЛЬНАЯ ТАБЛИЦА
- 31. 9.а. Анализ конечной таблицы ПРИЗНАК
- 32. 9.б. Анализ конечной таблицы ПРИЗНАК единственности
- 33. 9.в. Анализ конечной таблицы
- 34. 9.г. Анализ оценки дополнительной переменной x3
- 35. Оптимальное значение критерия при этом получит
- 36. Напротив, увеличение использования этого ресурса на
- 37. ТЕМА 1-ГО ПРАКТИЧЕСКОГО ЗАНЯТИЯ «ГРАФИЧЕСКАЯ МОДЕЛЬ ЗАДАЧИ ЛП»
Слайд 1СИМПЛЕКСНЫЙ МЕТОД
решения (анализа) задачи ЛП
ПРИМЕР ИСХОДНОЙ ЗАДАЧИ ЛП
КАНОНИЧЕСКАЯ ФОРМА ЗАДАЧИ
МАТРИЧНАЯ
Слайд 6
5. БАЗИСНАЯ
ФОРМА ЗАДАЧИ ЛП
ПРЕДПОЧИТАЕМАЯ, СИМПЛЕКСНАЯ
опорный план
L = 0 – (– 5x1 – 8x2) L = 0
Слайд 11
6. ОЦЕНКИ
НЕБАЗИСНЫХ ПЕРЕМЕННЫХ
Оценка Δi небазисной переменной xi
численно равна величине приращения
текущего значения критерия, соответствующее единичному приращению данной переменной:
ΔL = Δi ~ Δxi=+1.
В строке критерия оценки указаны
с обратным знаком !
ΔL = Δi ~ Δxi=+1.
В строке критерия оценки указаны
с обратным знаком !
Слайд 13Если текущий опорный план содержит перспективные переменные, то его можно улучшить
путем включения в базис любой из имеющихся перспективных переменных.
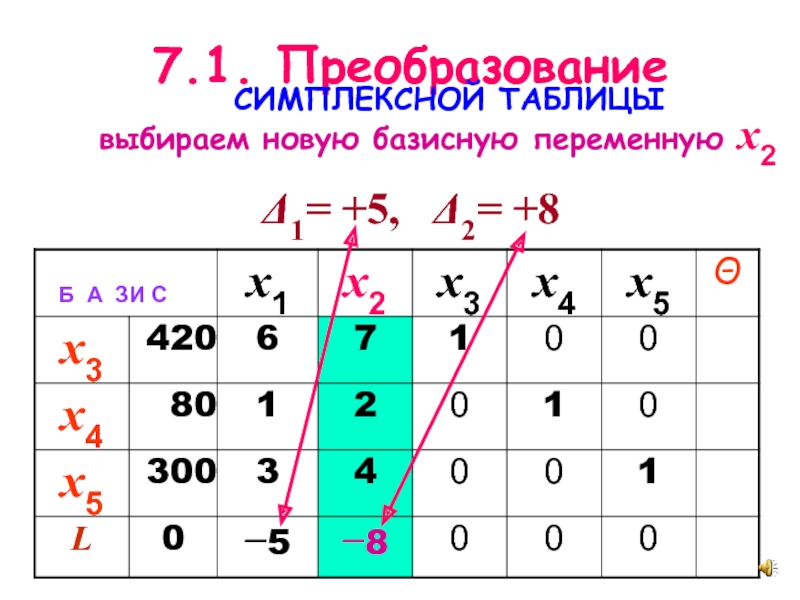
Слайд 147.1. Преобразование СИМПЛЕКСНОЙ ТАБЛИЦЫ выбираем новую базисную
переменную x2
Δ1= +5, Δ2= +8
Слайд 16Величина симплексного отношения указывает максимально возможное значение новой базисной переменной, «
разрешенное » соответствующим уравнением.
Симплексное отношение для строки (уравнения) не существует, если в разрешающем столбце этой строки находится нуль или отрицательное число.
Слайд 17Признак неограниченности критерия
Если получена очередная таблица, для которой не найдено ни
одного симплексного отношения, решение задачи ЛП не существует по причине неограниченности критерия.
Слайд 19
7.3. Преобразование
разрешающей строки производится путем ее деления на разрешающий элемент
x2
= 40 − (0,5 x1 + 0,5 x4)
Слайд 207.4а. Преобразование
остальных строк
Из преобразуемой строки вычитается
преобразованная разрешающая строка,
умноженная на элемент разрешающего столбца преобразуемой строки.
Слайд 31
9.а. Анализ конечной таблицы
ПРИЗНАК ОПТИМАЛЬНОСТИ
Если все небазисные переменные имеют отрицательную оценку,
то текущий опорный план оптимален.
В финальной таблице
имеем:
Δ3=- 0,4 < 0;
Δ4=-2,6 < 0.
В финальной таблице
имеем:
Δ3=- 0,4 < 0;
Δ4=-2,6 < 0.
Слайд 32
9.б. Анализ конечной таблицы
ПРИЗНАК единственности
оптимального плана
Если в оптимальном опорном
плане все небазисные переменные имеют ненулевую оценку, то этот план является ЕДИНСТВЕННЫМ оптимальным.
Слайд 33
9.в. Анализ конечной таблицы
ПРИЗНАК множества оптимальных планов
Если в
оптимальном опорном плане имеются небазисные переменные с нулевой оценкой, то существует бесконечно много оптимальных планов.
Слайд 349.г. Анализ оценки
дополнительной переменной
x3 ⎯ остаток ресурса №1
Небазисная переменная x3*
= 0.
Ее оценка Δ3 = − 0,4.
Увеличение этой переменной, например придание ей значения
x3 = 1,
соответствует уменьшению использования ресурса. Из имеющихся 420 единиц будет затрачено
420 − 1 = 419 единиц.
Ее оценка Δ3 = − 0,4.
Увеличение этой переменной, например придание ей значения
x3 = 1,
соответствует уменьшению использования ресурса. Из имеющихся 420 единиц будет затрачено
420 − 1 = 419 единиц.
Слайд 35 Оптимальное значение критерия при этом получит приращение ΔL = − 0,4. и
станет равным
376 − 0,4 = 375,6
Итак, при уменьшении использования ресурса на единицу оптимальное
значение критерия уменьшится на 0,4.
Слайд 36
Напротив, увеличение использования этого ресурса на 1, приведет к изменению оптимального
значения критерия на
ΔL = + 0,4.
Таким образом, оценка дополнительной переменной первого ограничения, взятая с обратным знаком, указывает численную меру
чувствительности критерия
к изменению доступного запаса ресурса.
Эта величина называется
«двойственная оценка ресурса».
ΔL = + 0,4.
Таким образом, оценка дополнительной переменной первого ограничения, взятая с обратным знаком, указывает численную меру
чувствительности критерия
к изменению доступного запаса ресурса.
Эта величина называется
«двойственная оценка ресурса».