- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной. Монотонность функции. Точки экстремума, экстремумы функции презентация
Содержание
- 1. Применение производной. Монотонность функции. Точки экстремума, экстремумы функции
- 2. Содержание Монотонность функции Точки экстремума, экстремумы функции
- 3. Монотонность функции Функция f возрастает на
- 4. Монотонность функции Функция f убывает на
- 5. Достаточный признак возрастания (убывания)функции Если f‘ (x)>
- 6. Исследование функции на монотонность с помощью производной
- 7. Функция y=f(x) задана на отрезке [a;
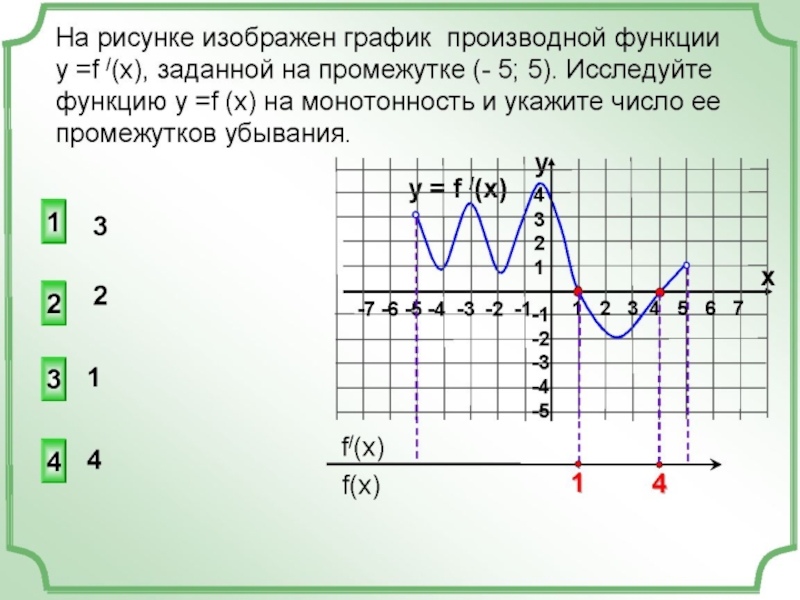
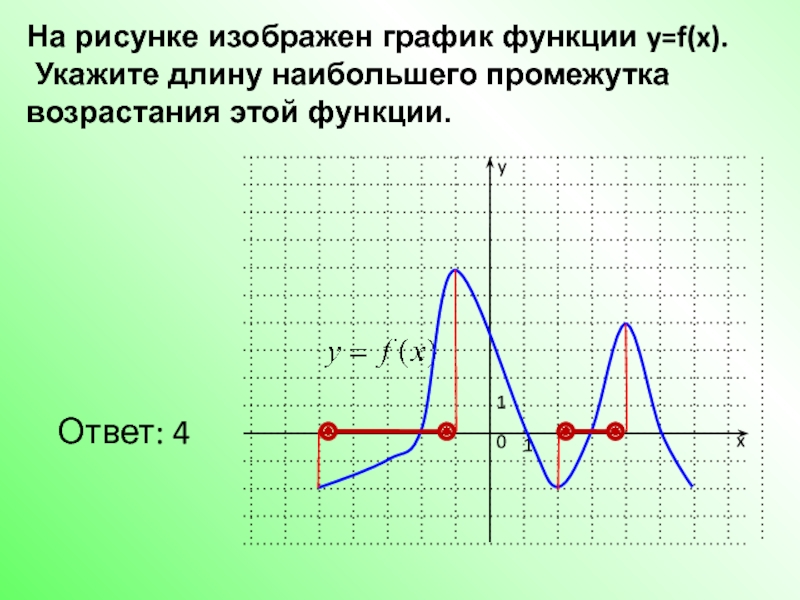
- 10. На рисунке изображен график функции y=f(x).
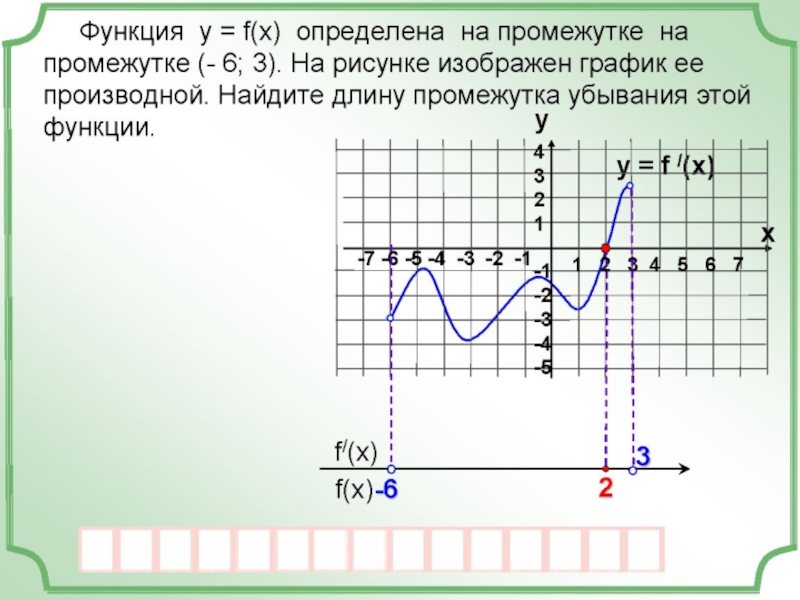
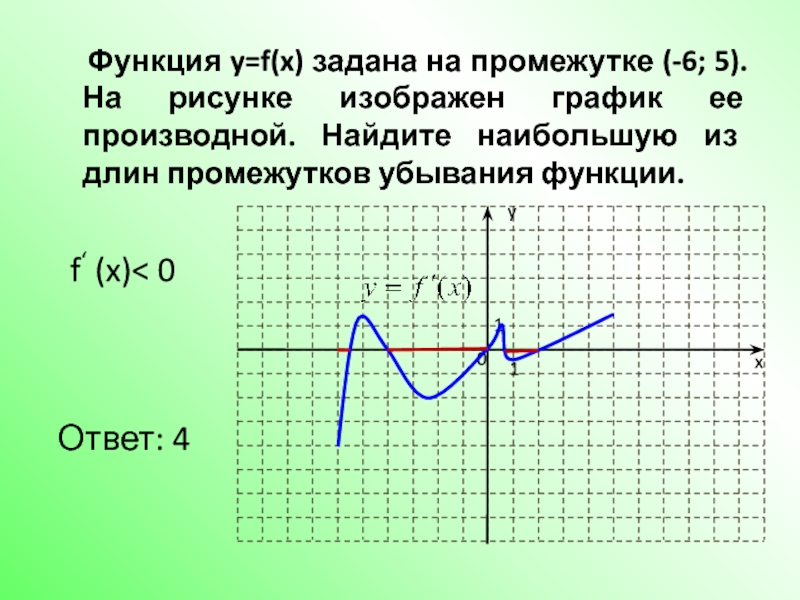
- 11. Функция y=f(x) задана на промежутке (-6;
- 12. Точки экстремума. Экстремумы функции.
- 13. Точки экстремума, экстремумы функции Точка x0 называется
- 14. Точки экстремума, экстремумы функции Точка x0 называется
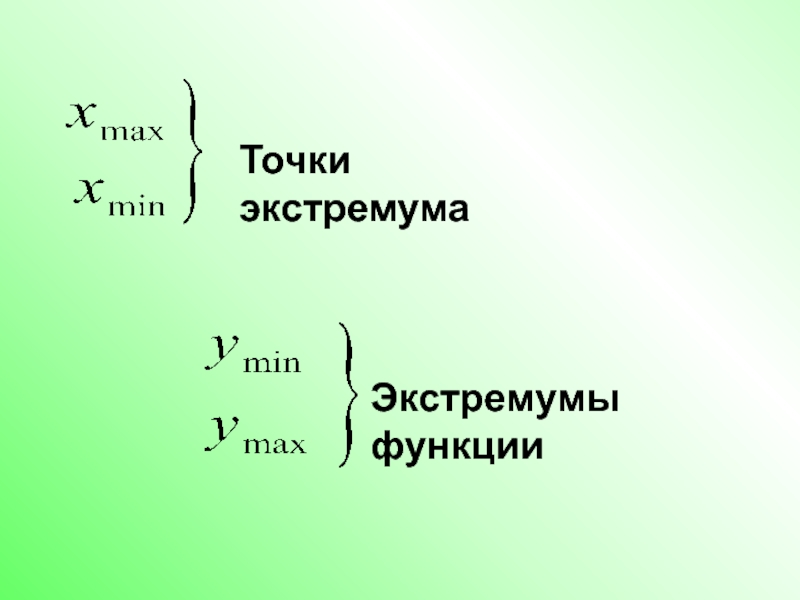
- 15. Точки экстремума Экстремумы функции
- 16. Критические точки Внутренние точки области определения функции,
- 17. Признак максимума функции. Если функция f непрерывна
- 18. Признак минимума функции. Если функция f непрерывна
- 19. Пример Найдите точки экстремума функции f(x)=3x-x3
- 20. График функции
Слайд 3Монотонность функции
Функция f возрастает на множестве P, если для любых x1
f(x1)> f (x2 )
Повторим теорию
y
y
1
1
0
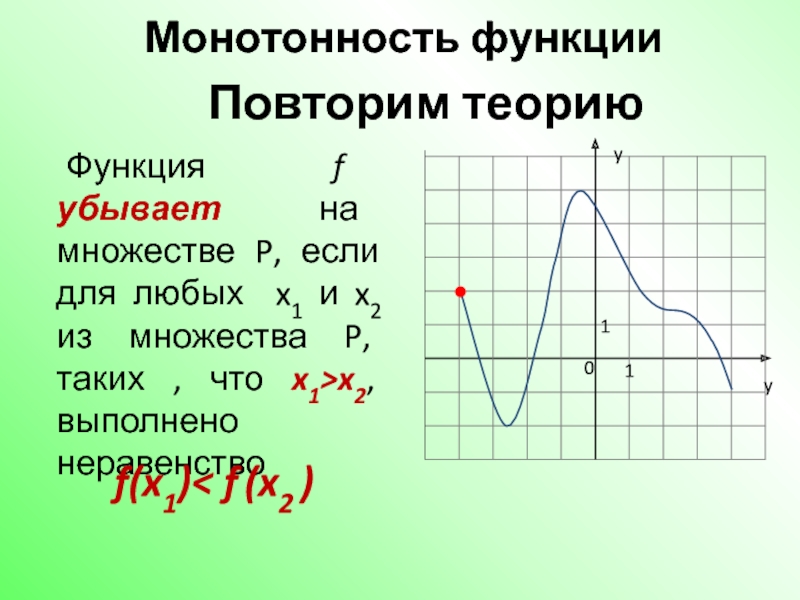
Слайд 4Монотонность функции
Функция f убывает на множестве P, если для любых x1
f(x1)< f (x2 )
Повторим теорию
y
y
1
1
0
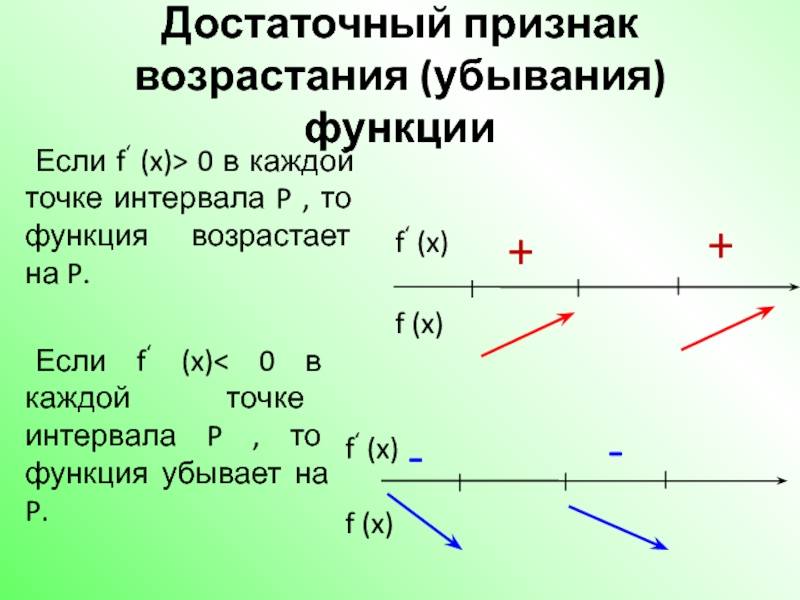
Слайд 5Достаточный признак возрастания (убывания)функции
Если f‘ (x)> 0 в каждой точке интервала
Если f‘ (x)< 0 в каждой точке интервала P , то функция убывает на P.
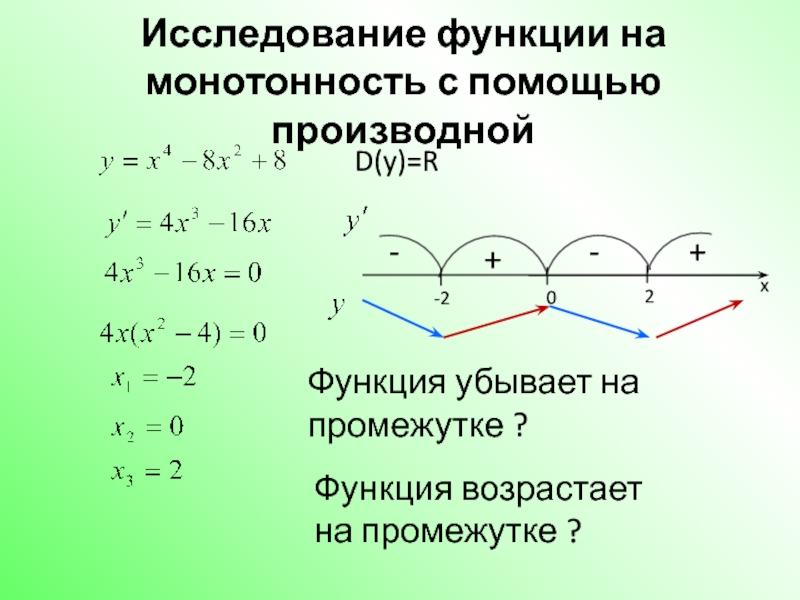
Слайд 6Исследование функции на монотонность с помощью производной
D(y)=R
x
Функция убывает на промежутке ?
Функция
+
-
+
-
Слайд 7
Функция y=f(x) задана на отрезке [a; b].На рисунке изображен график ее
y
a
b
Функция возрастает
f‘ (x)> 0
при
с
Функция убывает
f‘ (x)< 0
при
Ответ: 1
Слайд 10На рисунке изображен график функции y=f(x).
Укажите длину наибольшего промежутка возрастания
Ответ: 4
Слайд 11 Функция y=f(x) задана на промежутке (-6; 5).На рисунке изображен график
y
x
1
1
0
f‘ (x)< 0
Ответ: 4
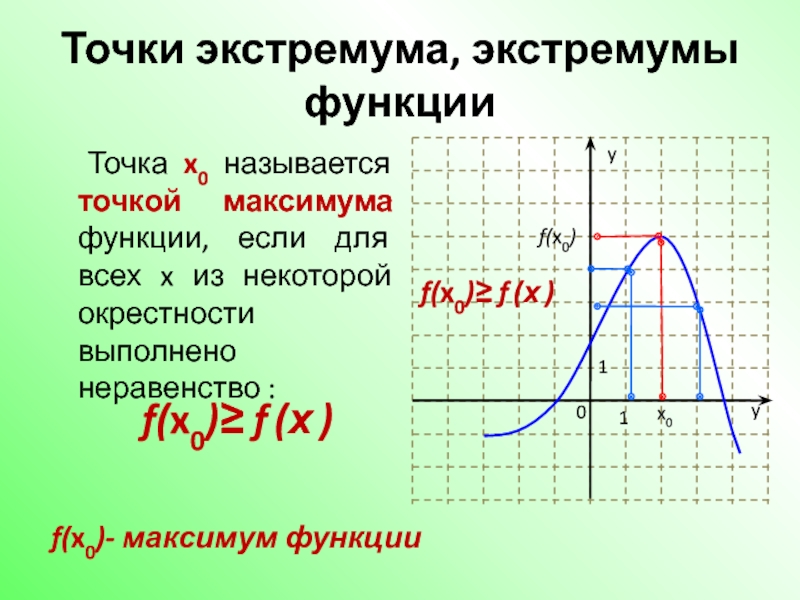
Слайд 13Точки экстремума, экстремумы функции
Точка x0 называется точкой максимума функции, если для
f(x0)- максимум функции
f(x0)≥ f (х )
x0
f(x0)
f(x0)≥ f (х )
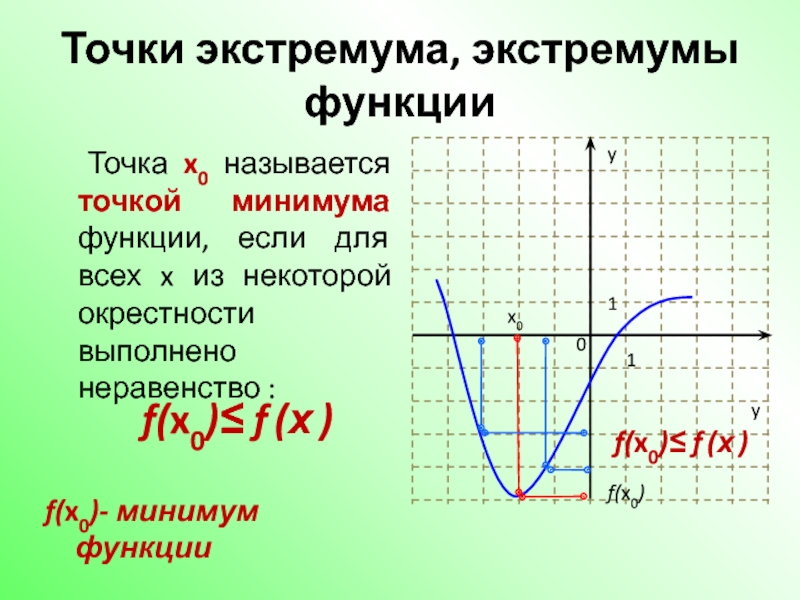
Слайд 14Точки экстремума, экстремумы функции
Точка x0 называется точкой минимума функции, если для
f(x0)- минимум функции
f(x0)≤ f (х )
x0
f(x0)
f(x0)≤ f (х )
Слайд 16Критические точки
Внутренние точки области определения функции, в которых ее производная равна
Необходимое условие экстремума
Если точка x0 является точкой экстремума функции f и в этой точке существует производная f‘ (x), то она равна нулю:
f‘ (x)= 0
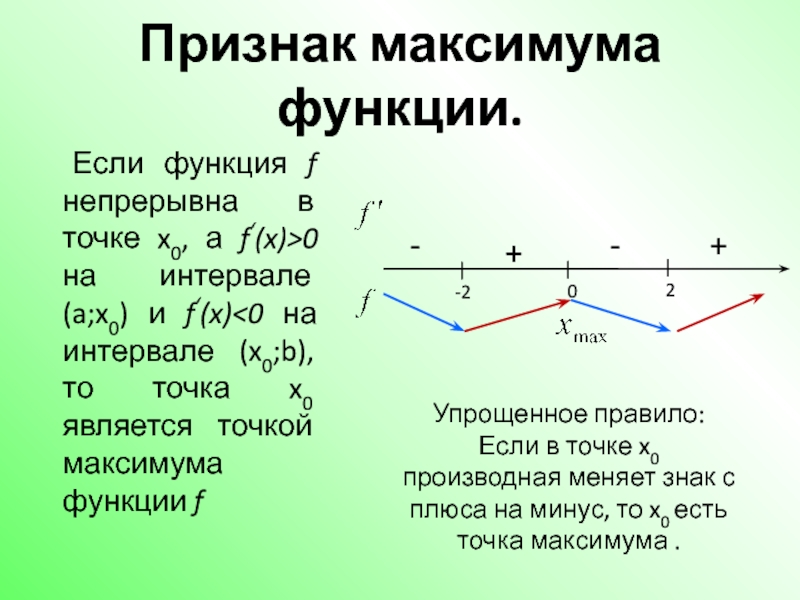
Слайд 17Признак максимума функции.
Если функция f непрерывна в точке x0, а f‘(x)>0
Упрощенное правило:
Если в точке x0 производная меняет знак с плюса на минус, то x0 есть точка максимума .
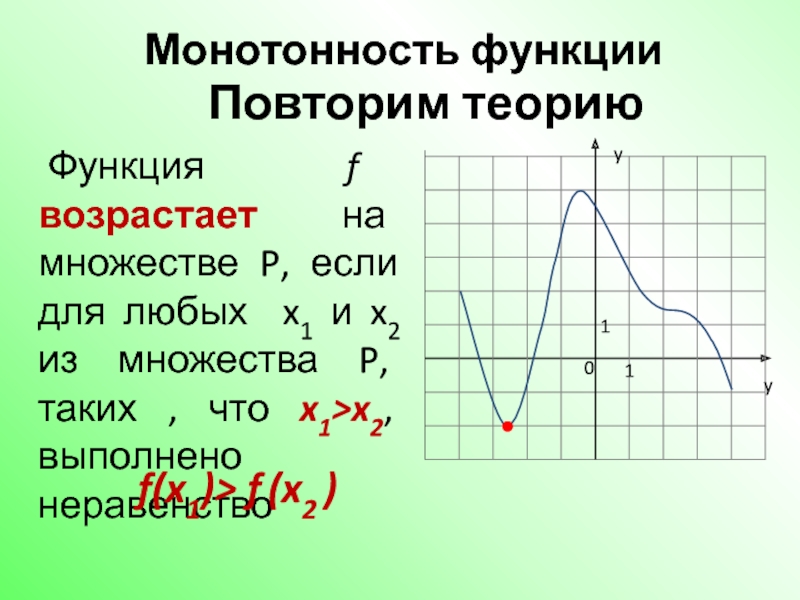
Слайд 18Признак минимума функции.
Если функция f непрерывна в точке x0, а f‘(x)
Упрощенное правило:
Если в точке x0 производная меняет знак с минуса на плюс, то x0 есть точка минимума .
Слайд 19Пример
Найдите точки экстремума функции
f(x)=3x-x3
D(y)=R
Ответ:
f‘ (x)= 0
x=±1
f‘ (x)- не
Таких значений x нет.
f‘ (x)=3-3x2
x
Критические точки


![Функция y=f(x) задана на отрезке [a; b].На рисунке изображен график ее производной. Исследуйте на монотонность](/img/tmb/5/434815/86bb34bb47fa610e43b3163861d400c8-800x.jpg)