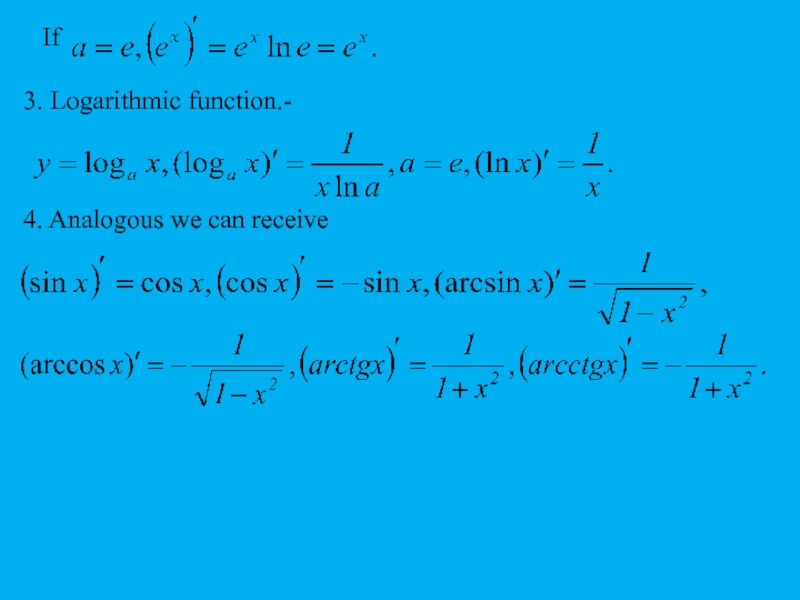Differential calculus of the function of one variable презентация

Gevorkyan
Professor of the Moscow State University of Economics, Statistics and Informatics
E-mail: EGevorkyan@mesi.ru, gevor_mesi@mail.ru

at the point

Definition.- Let us the function defines in the some
neighborhood of the point and let the is some point of this
neighborhood. If there exists the limit of the ratio ,

when , then this limit calls the derivative of the function

at the point and designates as , or , or ,

or , or , or .

So we have

- increment of argument,

-increment
of function, then we receive

The geometrical meaning of the derivative of the function

Let us we have At this time have received the
increment (see the figure). We see, that in the

triangular ABC and then

where is the angle between
the OX axis and the tangent of the curve at the point

the
at the point is the tangent of the angle
between the OX axis and the tangent of the curve at the point

The physical meaning of the derivative of the function

It is the instantaneous velocity at the moment when we have
the nonuniform motion , that is

The equation of the tangent of the curve at the point

Let is the equation of the tangent of the curve at the
point As the point

belongs to the curve and the tangent

then we have the following system of equations

where is the distance covered.

we can receive
the equation for the tangent in the form

Unilateral derivatives.

Let us defines in the right-side neighborhood of the
point and exists the limit

right-side derivative

of the function at the point

Similarly we can define the left-side limit of the function
at the point

then we say, that the function
has the derivative at the point , that is

Example 1.-

In this case, it is easy to understand that

That is

a quadratic function

has the derivative at the point

Example 2.-

Here we have

That is, this function at the point

has no derivative.

continuity condition of the function
at the point that is or

or

and we have

Differentiability of .

Let defines in the interval and

at the point is named differentiable if the
increment of this function can be presented in a form
where is some
constant, and when

Theorem.- for differentiability of it is necessary and
sufficient, that it had finite derivative.
The proof of necessity.- Let the function is differentiable,
that is or

So we have

has finite
derivative, that is exists the limit



It means, that the difference

when Then we have
Now if we denote then we have

that required to be proved.

The differential of the function .

Let us is differentiable. At that time we have, that


The term is the linear part of the increment of the
function relative

and are the infinitely small
of the same order. But the quantity in compared with
is infinitely small of higher order, that is

So the term is the leading linear part of the increase
of the The term is named the differential

of the function and is indicated as
Note, that if we have the function then we receive
that is So we have



So we can say, that the derivative of the function is equal to the
ratio of and .

.

Let us turn to the figure which was for the determine the derivative

of the function We know, that

where is the angle between the curve and the tangent at the point

Then we have On the other hand



So we can say, that the differential is the increase of
the ordinate of the tangent to the curve at the point

.

Note, that all rules of calculating of derivatives of elementary
functions we can receive with help of definition of derivative of
the function.

1. The power function -
According to the definition of derivative we have

Opening brackets using the binomial theorem, after some transformations
we get the following rule

1. The indicative function -

After some transformations we get