Учитель математики Потапова Е.А.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразования графиков функций презентация
Содержание
- 1. Преобразования графиков функций
- 3. Преобразование симметрии относительно оси х f(x)
- 5. Преобразование симметрии относительно оси y f(x)
- 7. Замечание 1. График четной функции не изменяется
- 8. Замечание 2. График нечетной функции изменяется одинаково
- 9. f(x) f(x) + b
- 10. Параллельный перенос вдоль оси х f(x)
- 12. Параллельный перенос вдоль оси y f(x)
- 16. Сжатие и растяжение вдоль оси x
- 17. Замечание. Точки пересечения графика с осью y остаются неизменными.
- 18. Сжатие и растяжение вдоль оси y
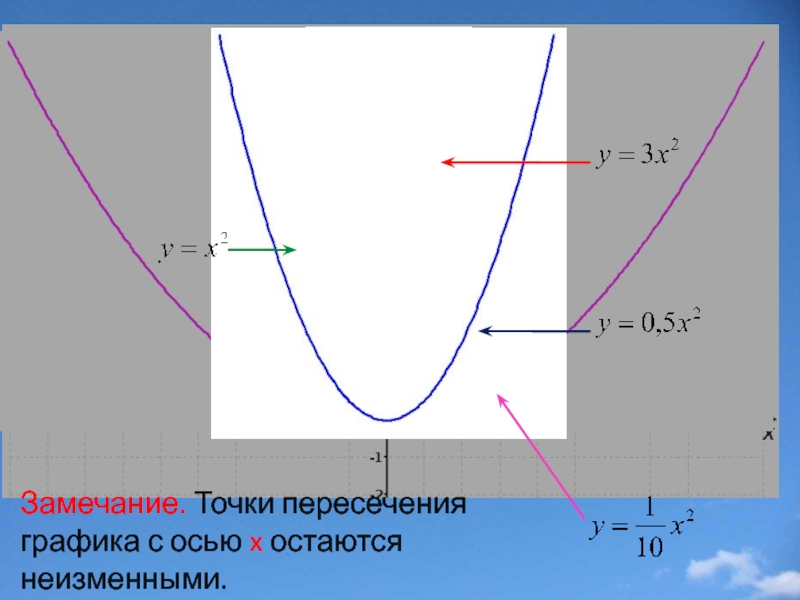
- 20. Замечание. Точки пересечения графика с осью x остаются неизменными.
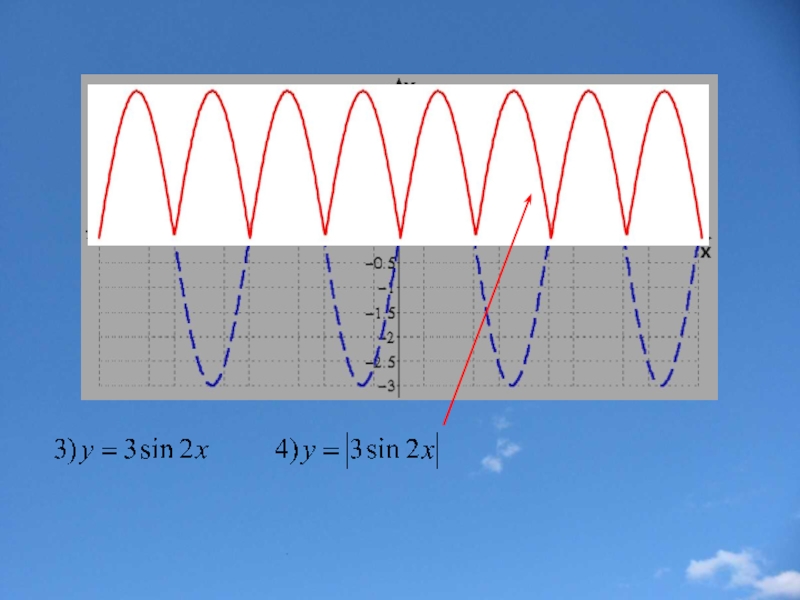
- 23. Построение графика функции у=|f(x)|
- 26. Построение графика функции у=f(|x|) Часть
- 30. Построение графика обратной функции
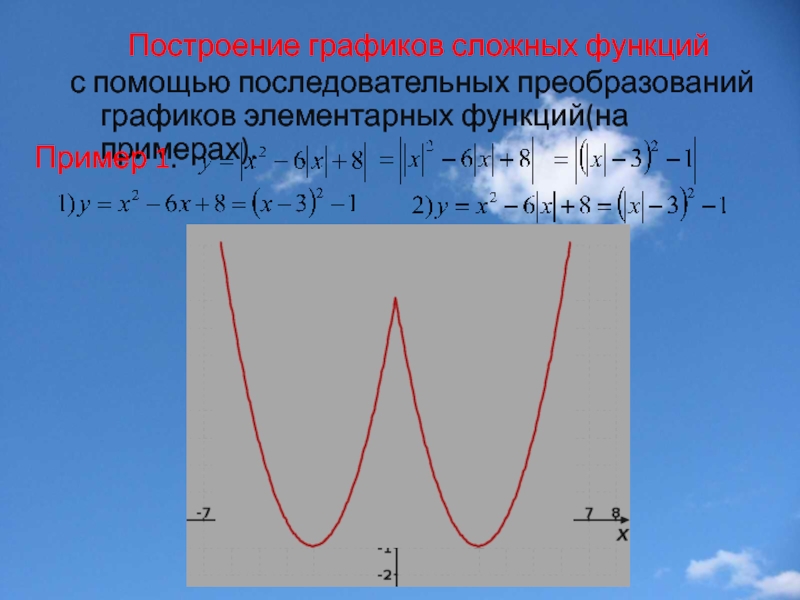
- 33. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций(на примерах). Пример 1.
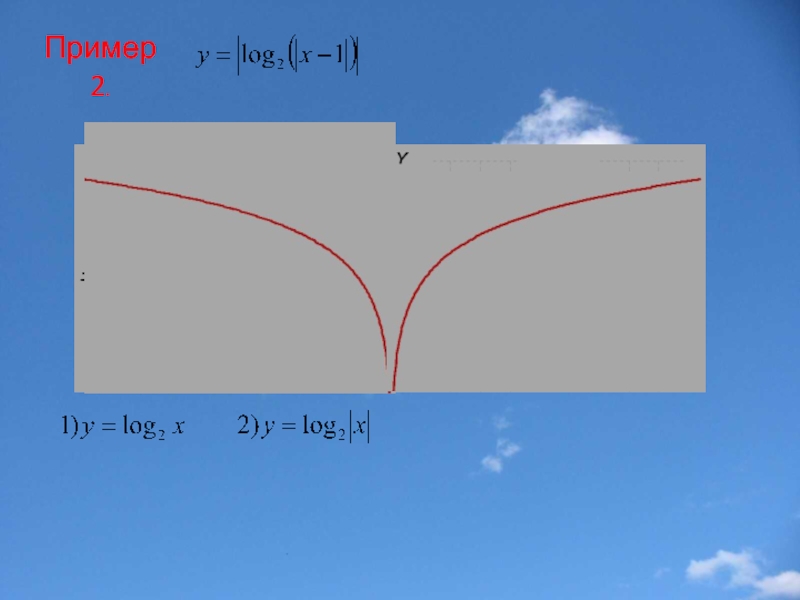
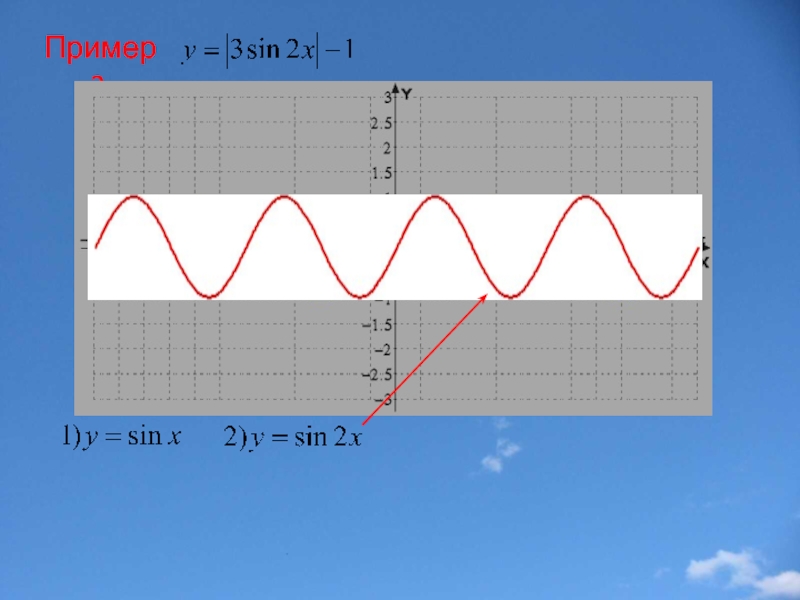
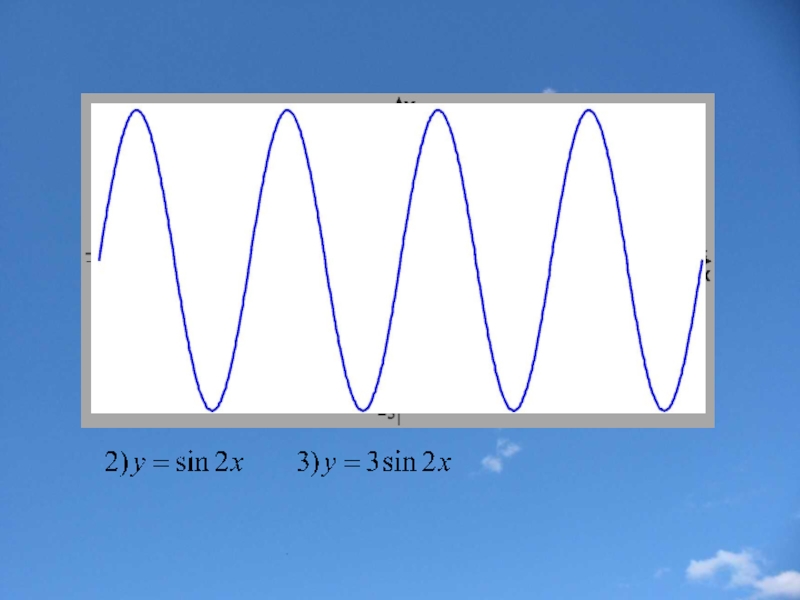
- 35. Пример 2.
- 38. Пример 3.
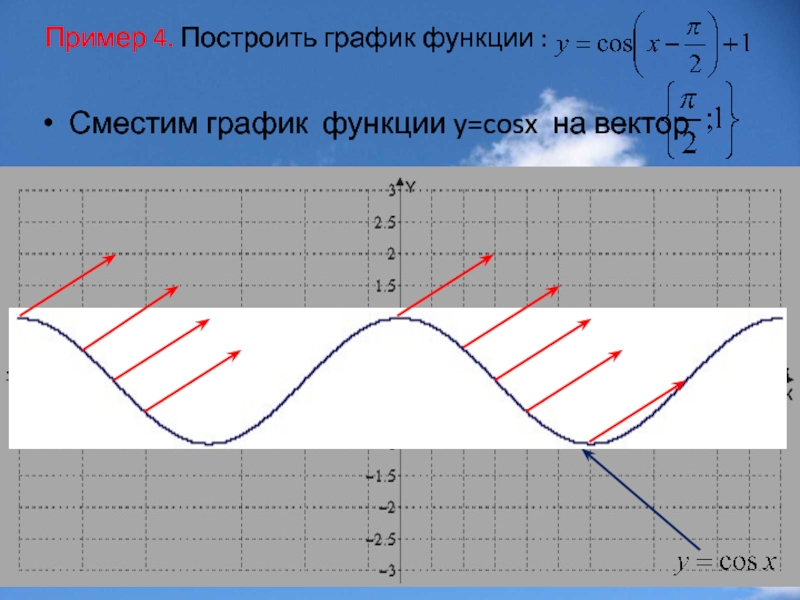
- 42. Пример 4. Построить график функции : Сместим график функции y=cosx на вектор
Преобразование симметрии относительно оси х
f(x) -f(x) График функции у = -f(x) получается преобразованием симметрии графика функции у = f(x) относительно оси х. Замечание. Точки пересечения графика с
Слайд 1Преобразования
графиков функций
Муниципальное
Общеобразовательное Учреждение «Средняя Общеобразовательная
Школа №236
г.Знаменск»
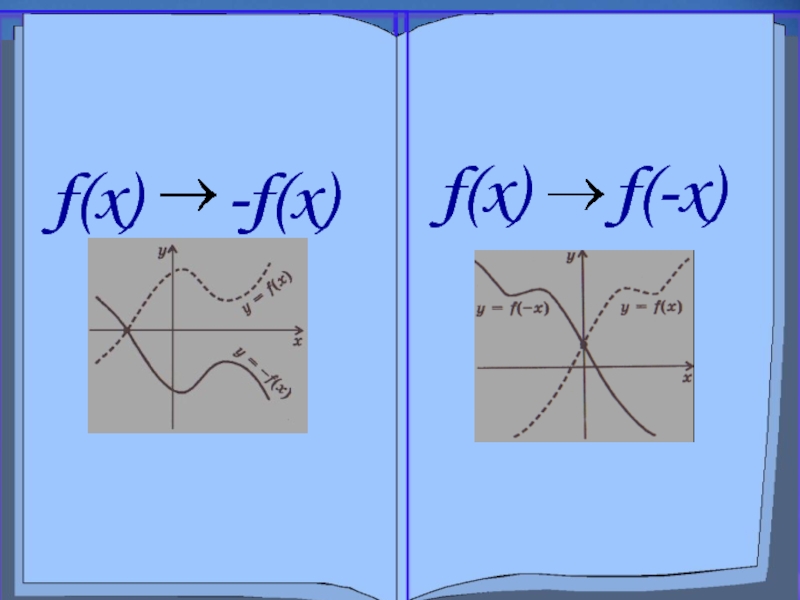
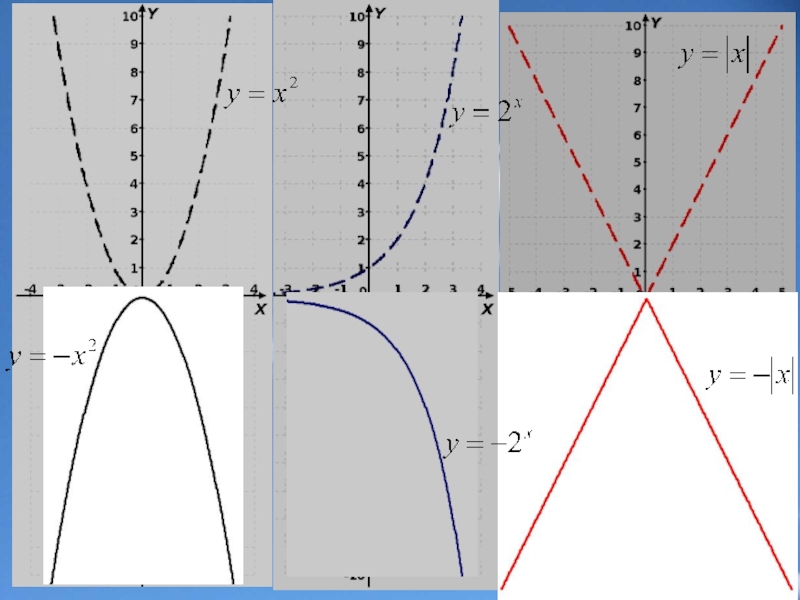
Слайд 3Преобразование симметрии относительно оси х
f(x) -f(x)
График функции у =
-f(x) получается преобразованием симметрии графика функции у = f(x) относительно оси х.
Замечание. Точки пересечения графика с осью х остаются неизменными.
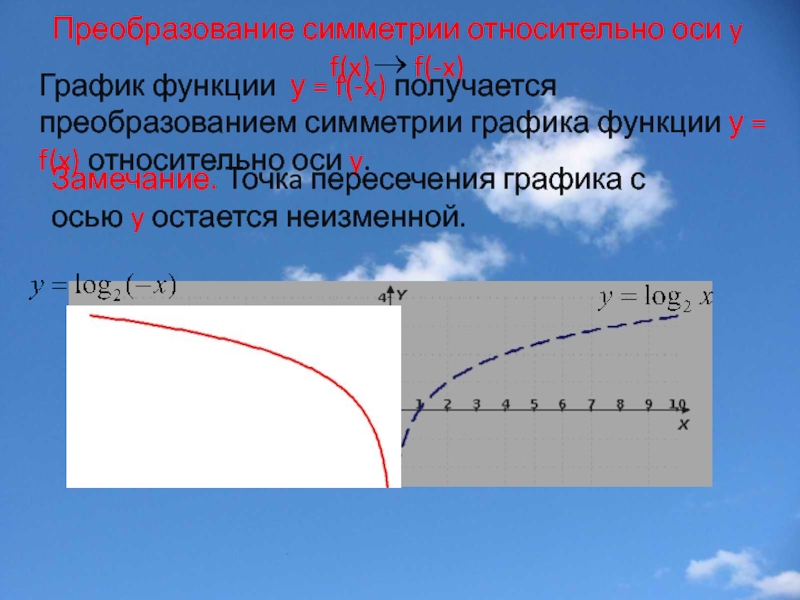
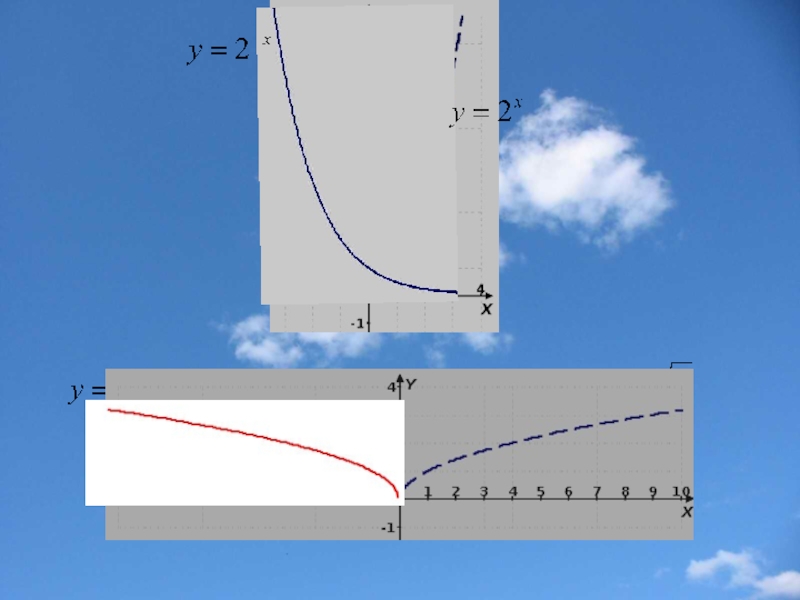
Слайд 5Преобразование симметрии относительно оси y
f(x) f(-x)
График функции у =
f(-x) получается преобразованием симметрии графика функции у = f(x) относительно оси y.
Замечание. Точкa пересечения графика с осью y остается неизменной.
Слайд 7Замечание 1.
График четной функции не изменяется при отражении относительно оси у,
поскольку для четной функции
f(-x)=f(x). Пример: (-x)2 = x2.
f(-x)=f(x). Пример: (-x)2 = x2.
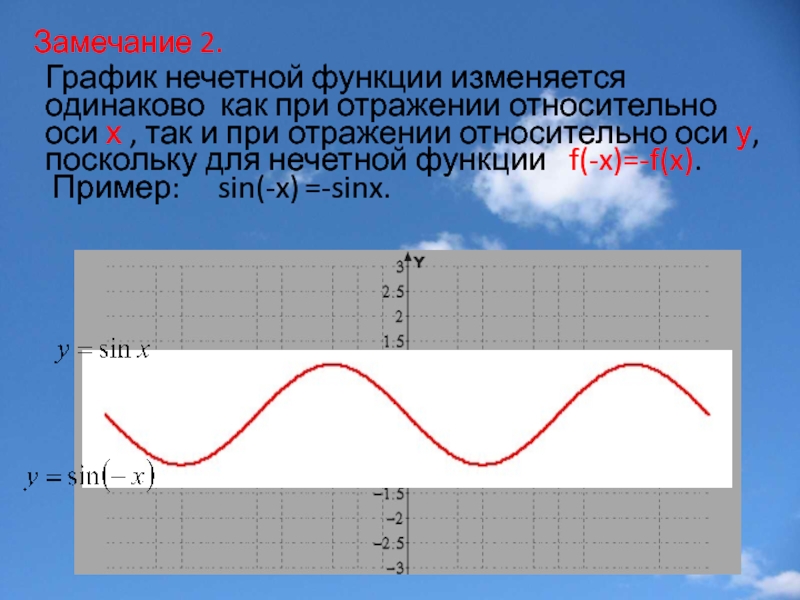
Слайд 8Замечание 2.
График нечетной функции изменяется одинаково как при отражении относительно оси
х , так и при отражении относительно оси у, поскольку для нечетной функции f(-x)=-f(x).
Пример: sin(-x) =-sinx.
Пример: sin(-x) =-sinx.
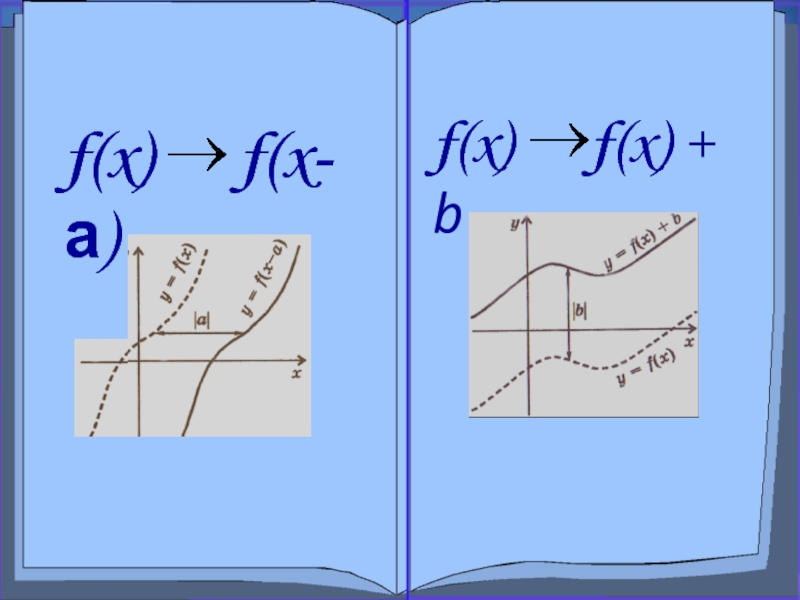
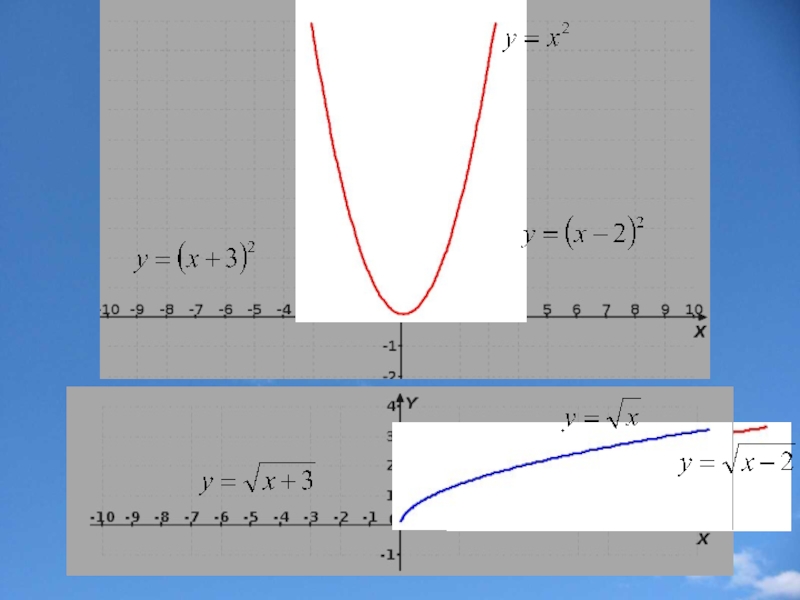
Слайд 10Параллельный перенос вдоль оси х
f(x) f(x-а)
График функции у
= f(x-а) получается параллельным переносом вдоль оси х на |a| вправо при а>0 и влево при а
Замечание: График периодической функции с периодом Т не изменяется при параллельных переносах вдоль оси х на nT, nϵN.
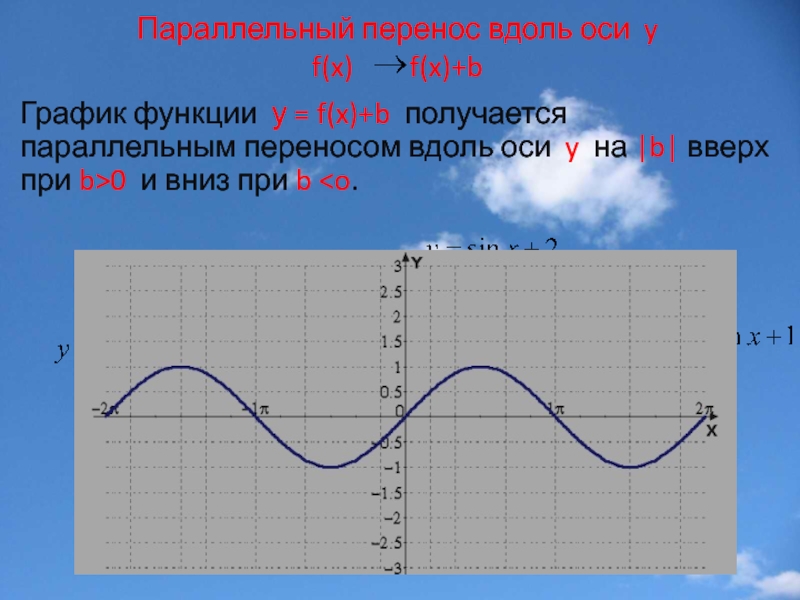
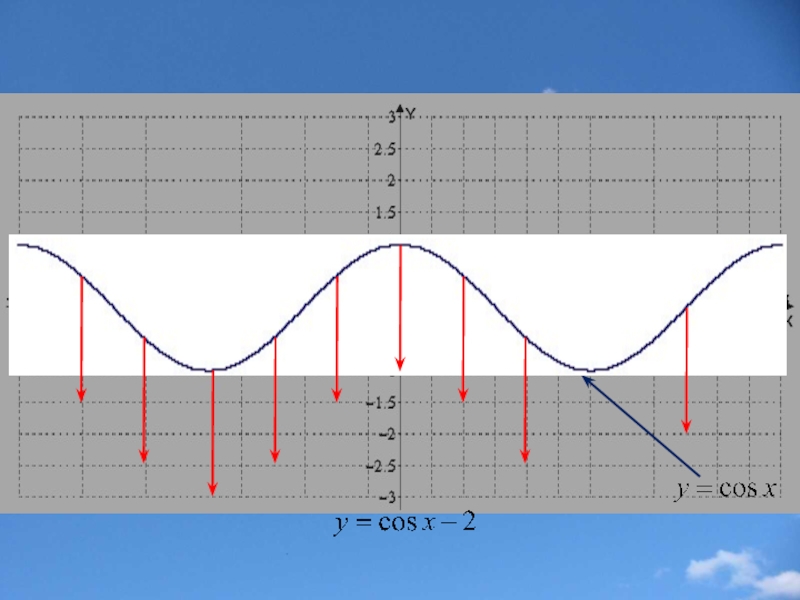
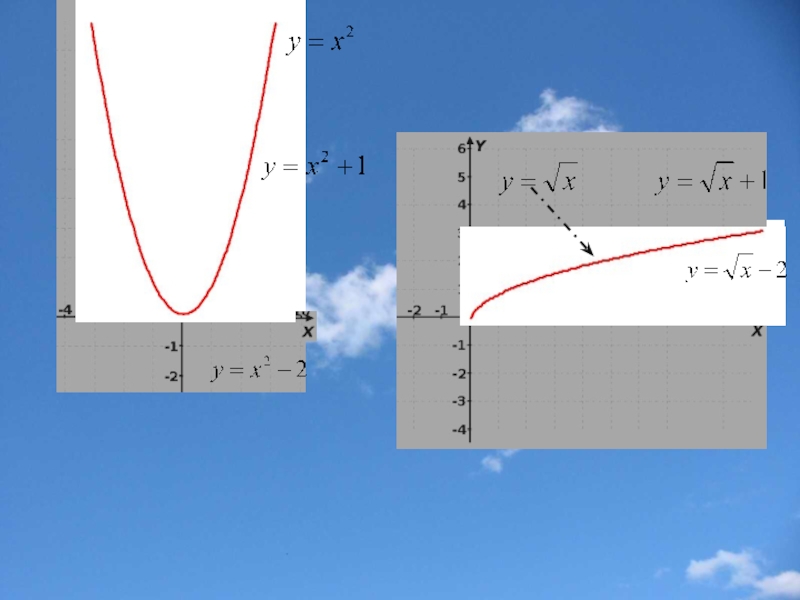
Слайд 12Параллельный перенос вдоль оси y
f(x) f(x)+b
График функции у
= f(x)+b получается параллельным переносом вдоль оси y на |b| вверх при b>0 и вниз при b
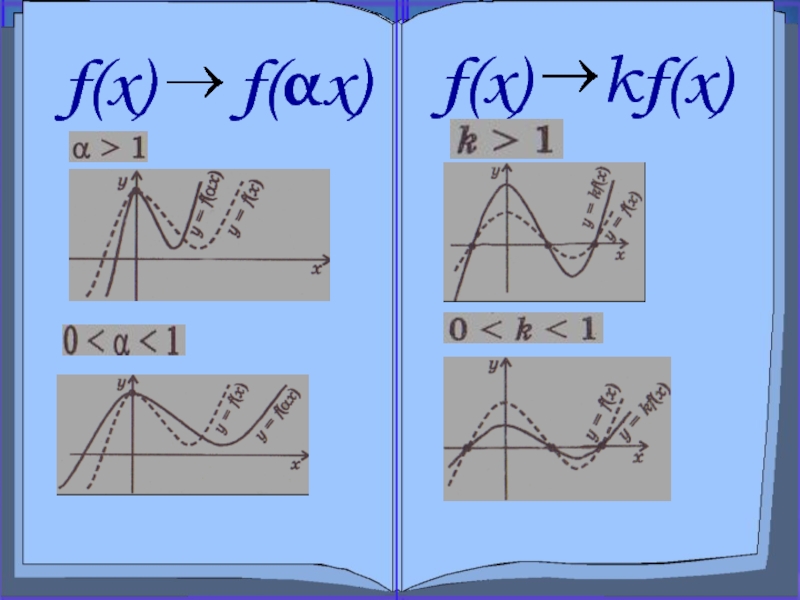
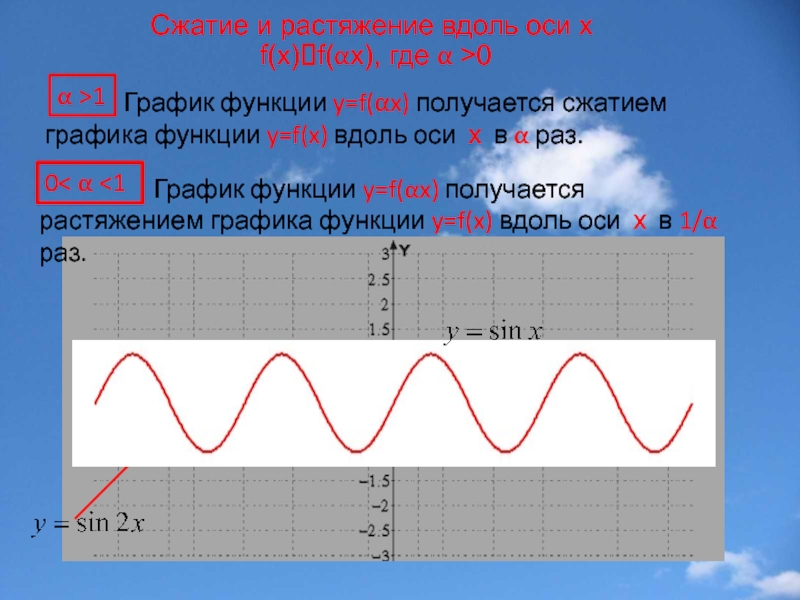
Слайд 16Сжатие и растяжение вдоль оси x
f(x)?f(αx), где α >0
График функции y=f(αx) получается сжатием графика функции y=f(x) вдоль оси х в α раз.
График функции y=f(αx) получается растяжением графика функции y=f(x) вдоль оси х в 1/α раз.
α >1
0< α <1
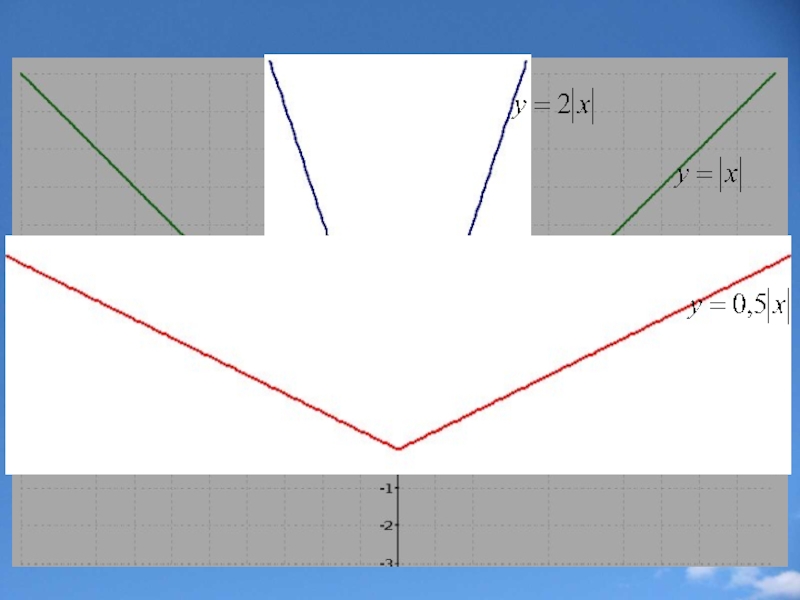
Слайд 18Сжатие и растяжение вдоль оси y
f(x)?kf(x), где k>0
График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.
График функции y=kf(x) получается сжатием графика функции y=f(x) вдоль оси y в 1/k раз.
k>1
0
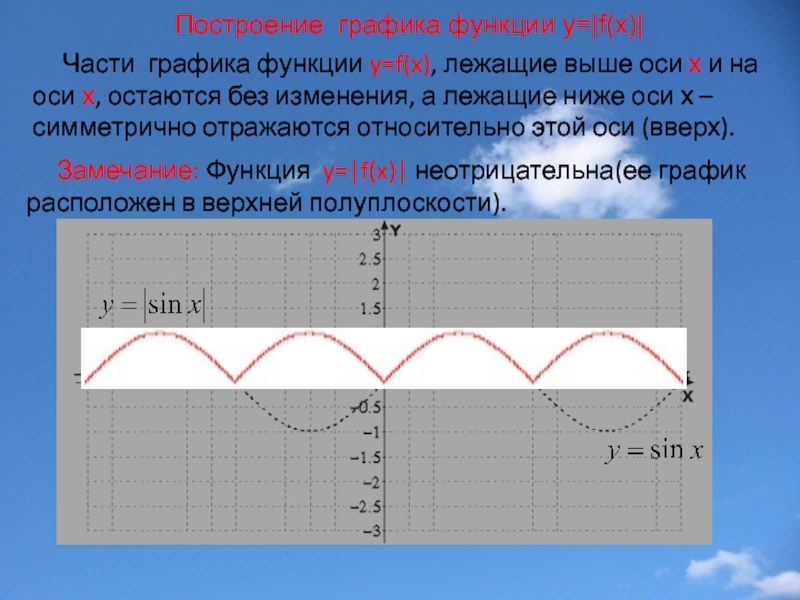
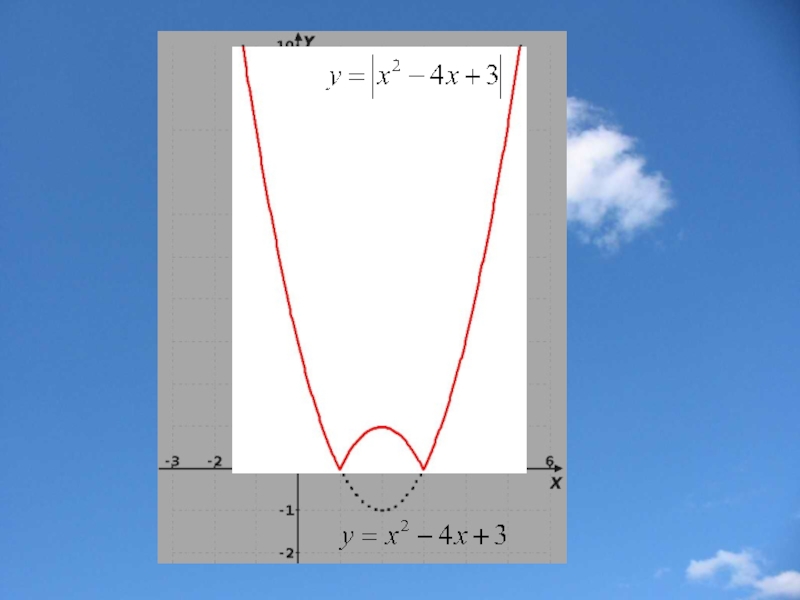
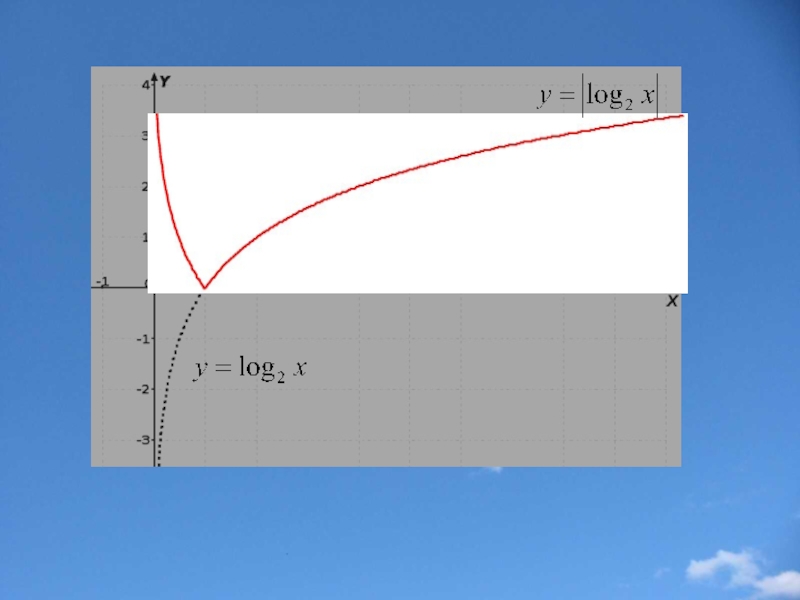
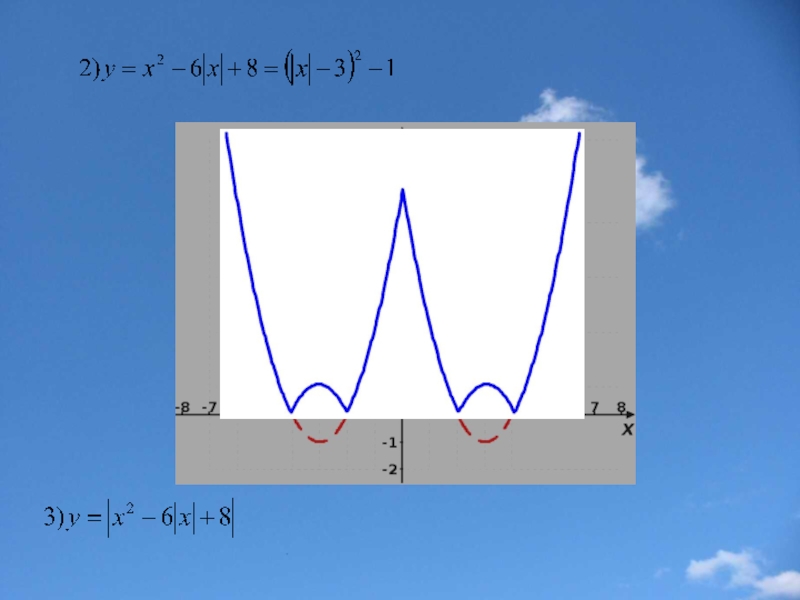
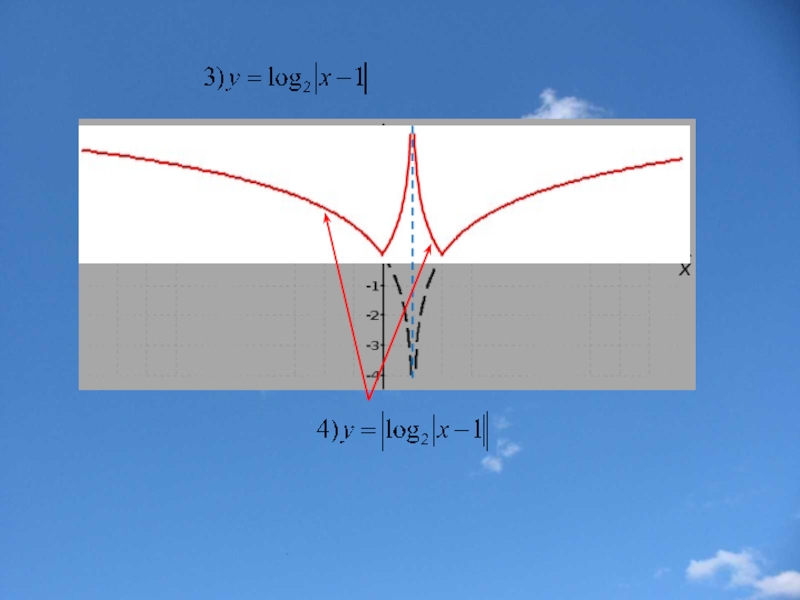
Слайд 23Построение графика функции у=|f(x)|
Части графика функции y=f(x), лежащие
выше оси х и на оси х, остаются без изменения, а лежащие ниже оси х –симметрично отражаются относительно этой оси (вверх).
Замечание: Функция y=|f(x)| неотрицательна(ее график расположен в верхней полуплоскости).
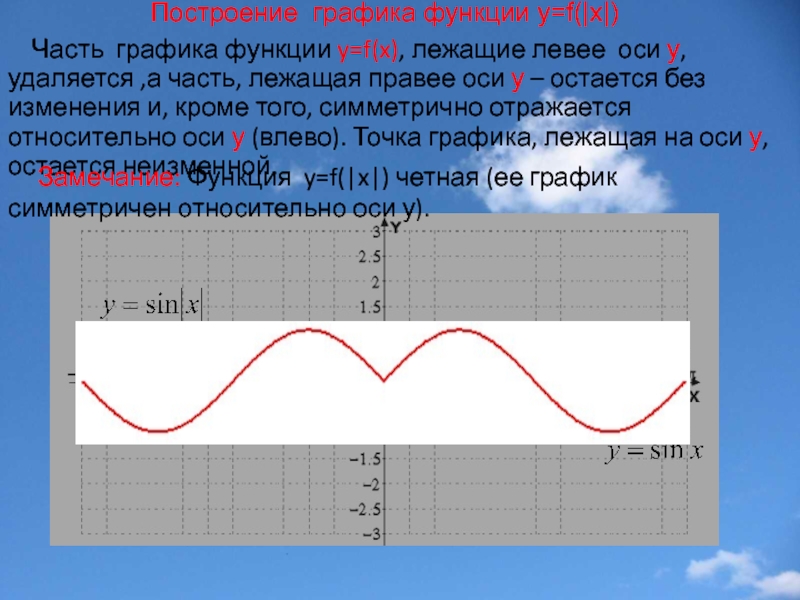
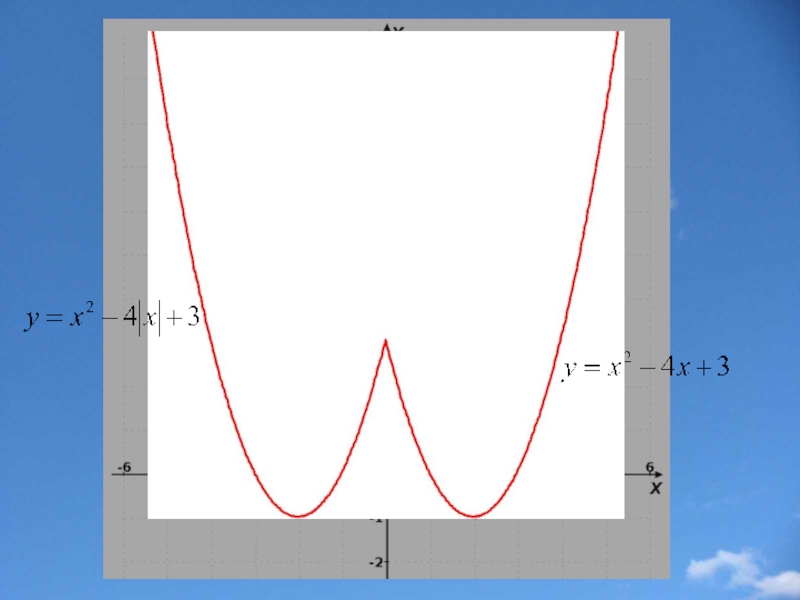
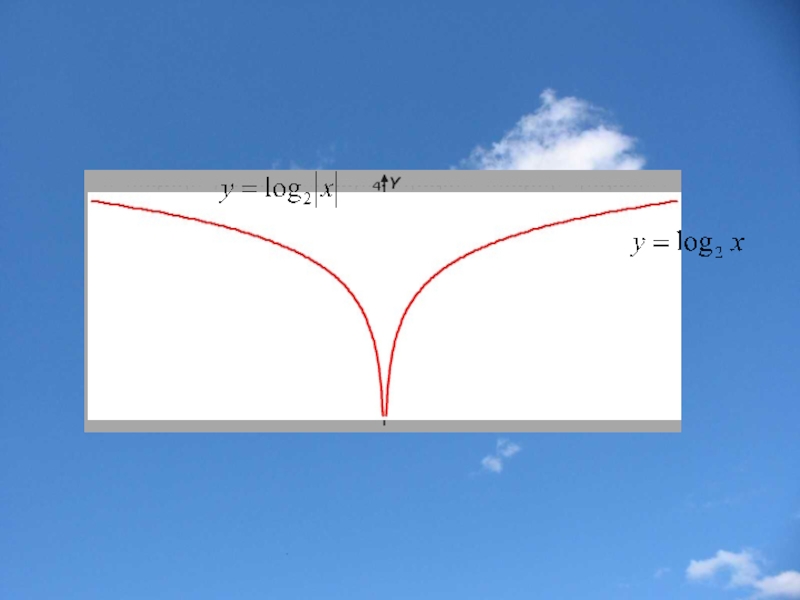
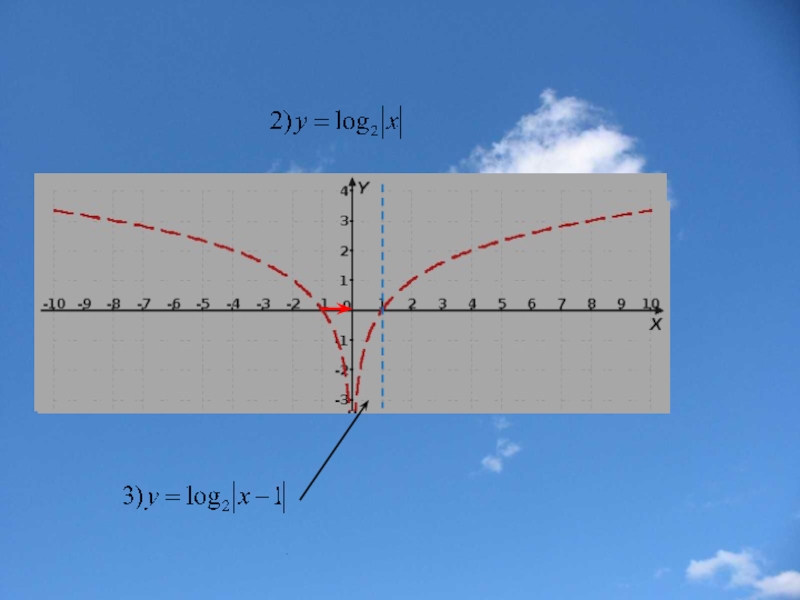
Слайд 26Построение графика функции у=f(|x|)
Часть графика функции y=f(x), лежащие левее
оси у, удаляется ,а часть, лежащая правее оси у – остается без изменения и, кроме того, симметрично отражается относительно оси у (влево). Точка графика, лежащая на оси у, остается неизменной.
Замечание: Функция y=f(|x|) четная (ее график симметричен относительно оси у).
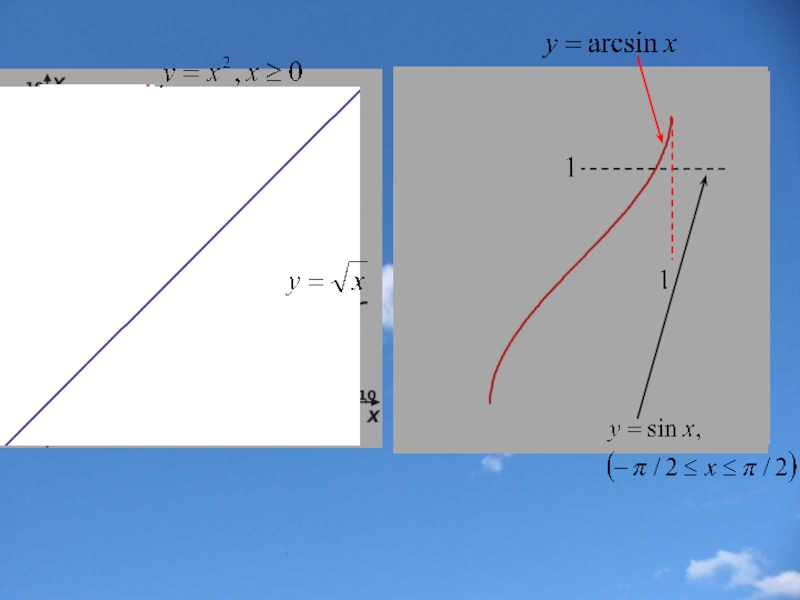
Слайд 30Построение графика обратной функции
График функции у
= g(x) , обратной для данной функции у = f(x) , можно получить преобразованием симметрии графика у = f(x) относительно прямой y=х.
Замечание. Описанное построение можно производить только для функции, имеющей обратную.
Примеры графиков
взаимно обратных функций:
Слайд 33Построение графиков сложных функций
с помощью последовательных преобразований графиков элементарных функций(на примерах).
Пример
1.
