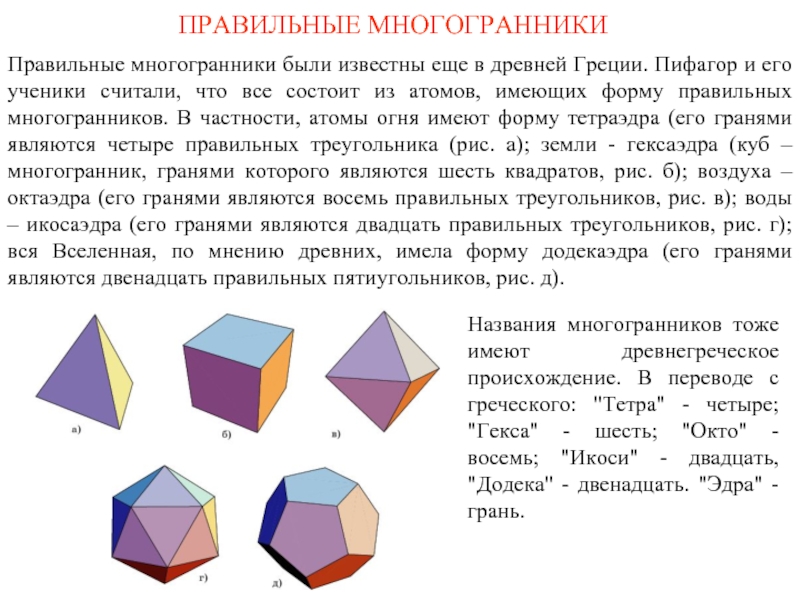
Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многогранники презентация
Содержание
- 1. Правильные многогранники
- 2. Кубок Кеплера Иоганн Кеплер (1571 –
- 3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Выпуклый многогранник называется правильным, если
- 4. ТЕТРАЭДР Наиболее простым правильным многогранником является треугольная
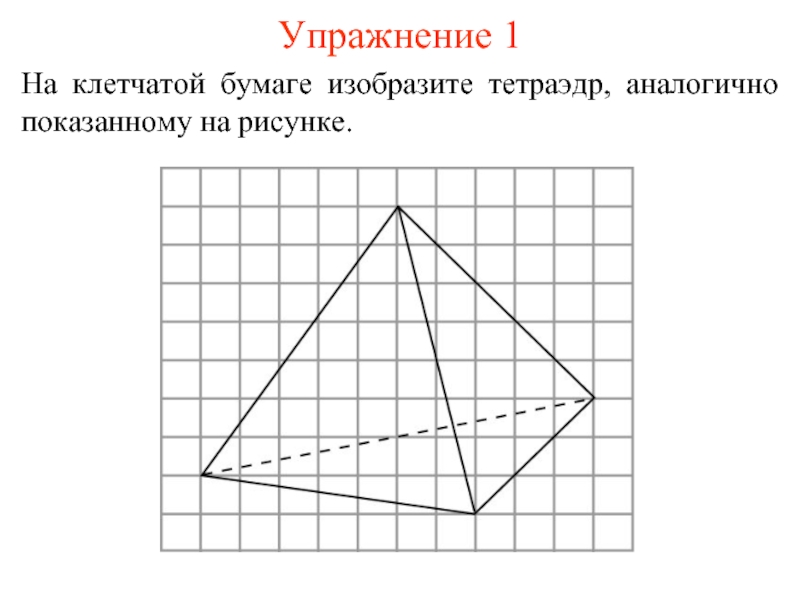
- 5. Упражнение 1 На клетчатой бумаге изобразите тетраэдр, аналогично показанному на рисунке.
- 6. КУБ (ГЕКСАЭДР) Многогранник, гранями которого являются квадраты
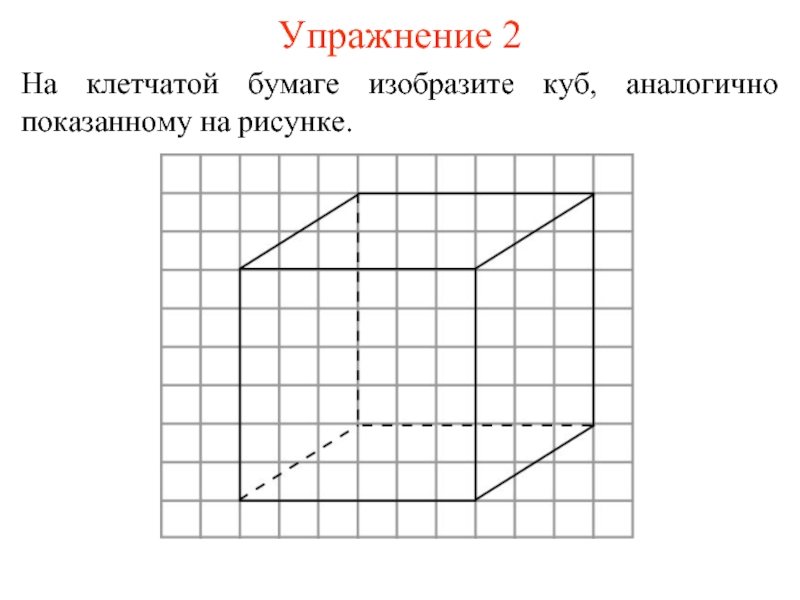
- 7. Упражнение 2 На клетчатой бумаге изобразите куб, аналогично показанному на рисунке.
- 8. ОКТАЭДР Многогранник, гранями которого являются правильные треугольники
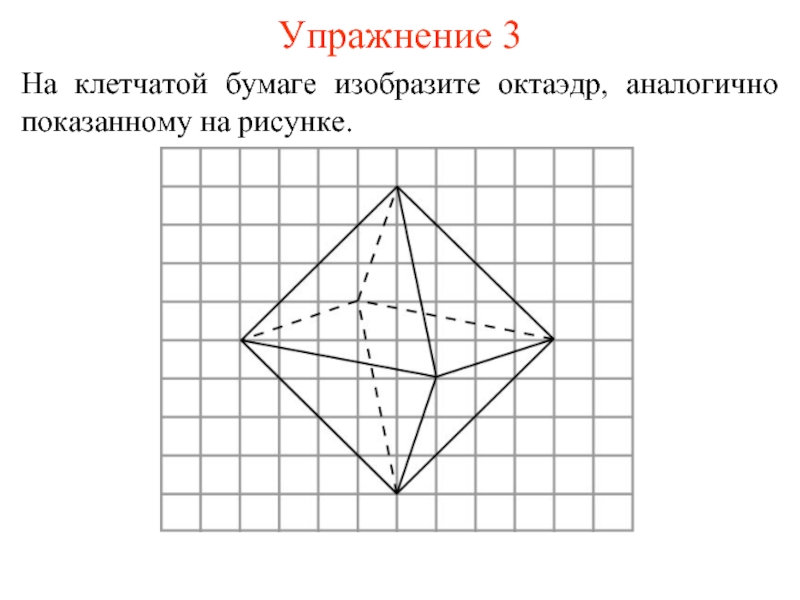
- 9. Упражнение 3 На клетчатой бумаге изобразите октаэдр, аналогично показанному на рисунке.
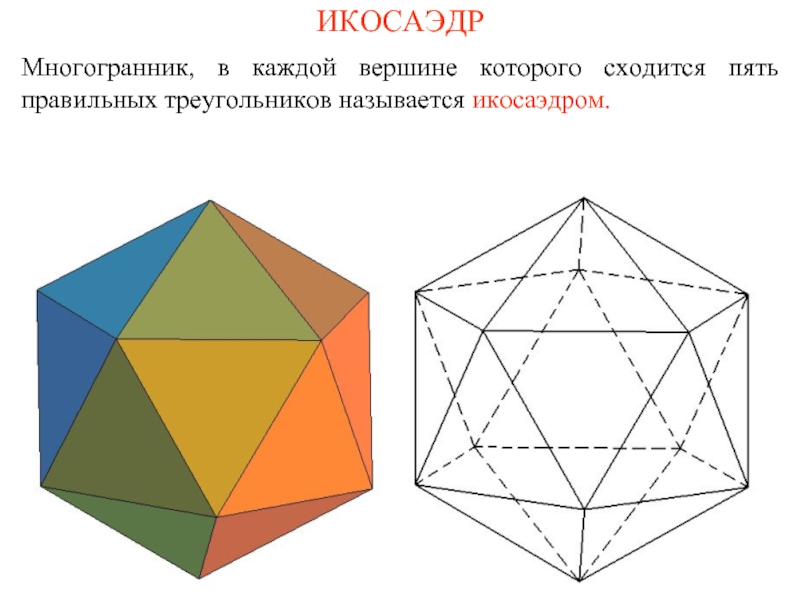
- 10. ИКОСАЭДР Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.
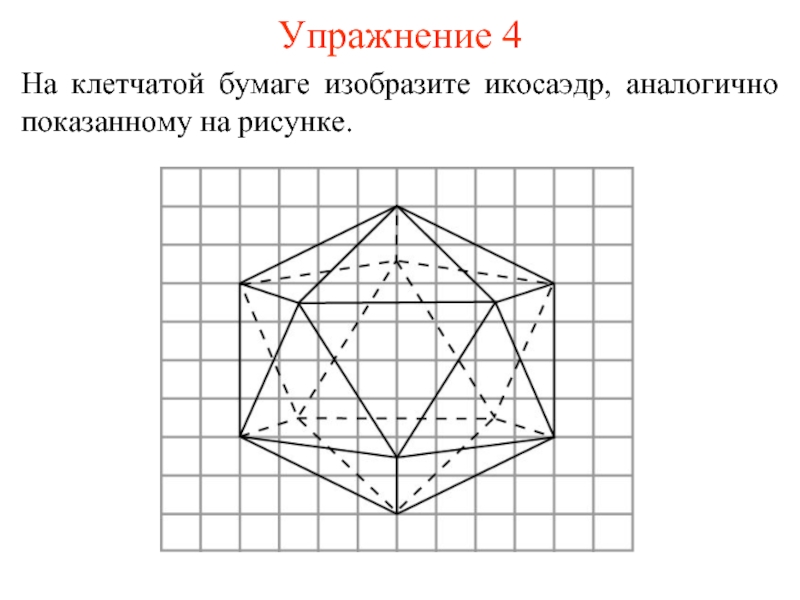
- 11. Упражнение 4 На клетчатой бумаге изобразите икосаэдр, аналогично показанному на рисунке.
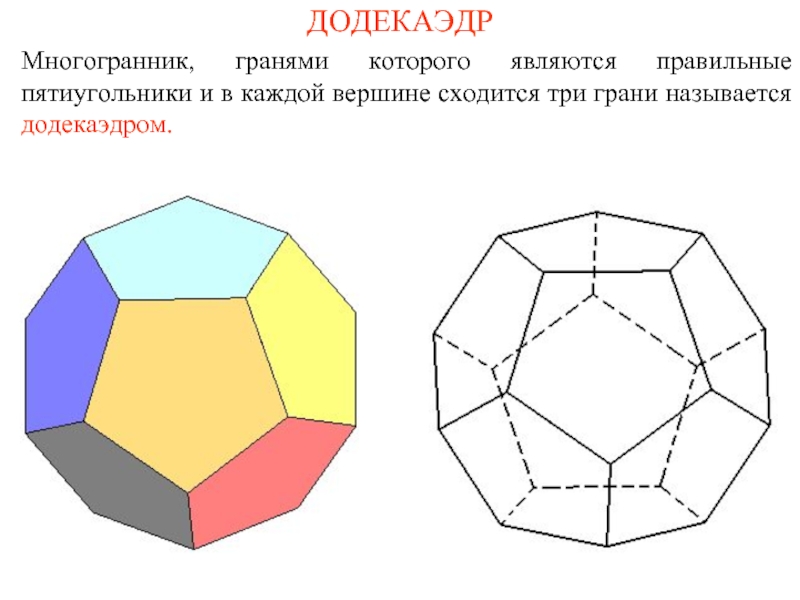
- 12. ДОДЕКАЭДР Многогранник, гранями которого являются правильные пятиугольники
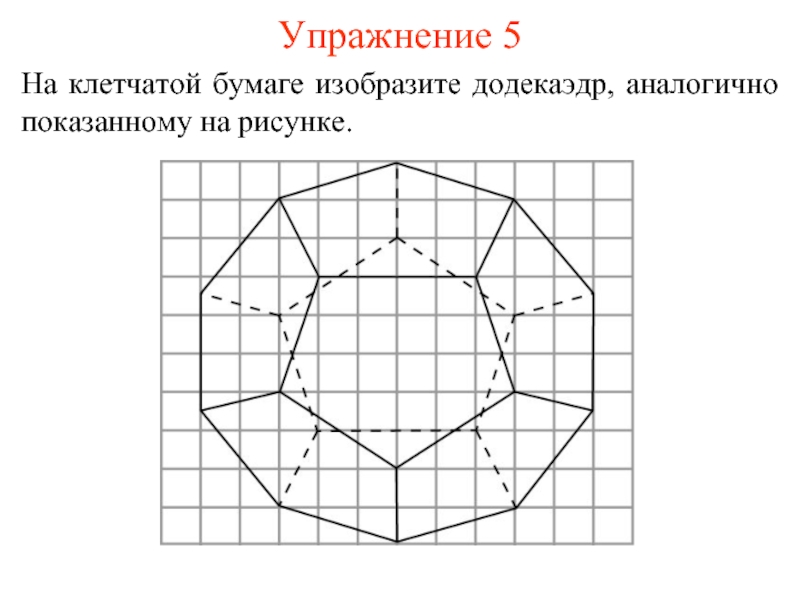
- 13. Упражнение 5 На клетчатой бумаге изобразите додекаэдр, аналогично показанному на рисунке.
- 14. Упражнение 6 Почему гранями правильного многогранника не
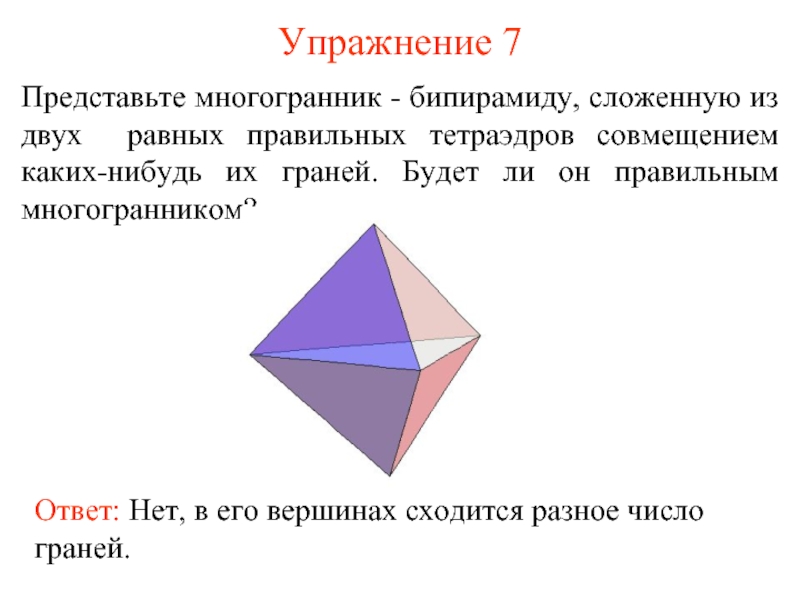
- 15. Упражнение 7 Представьте многогранник - бипирамиду, сложенную
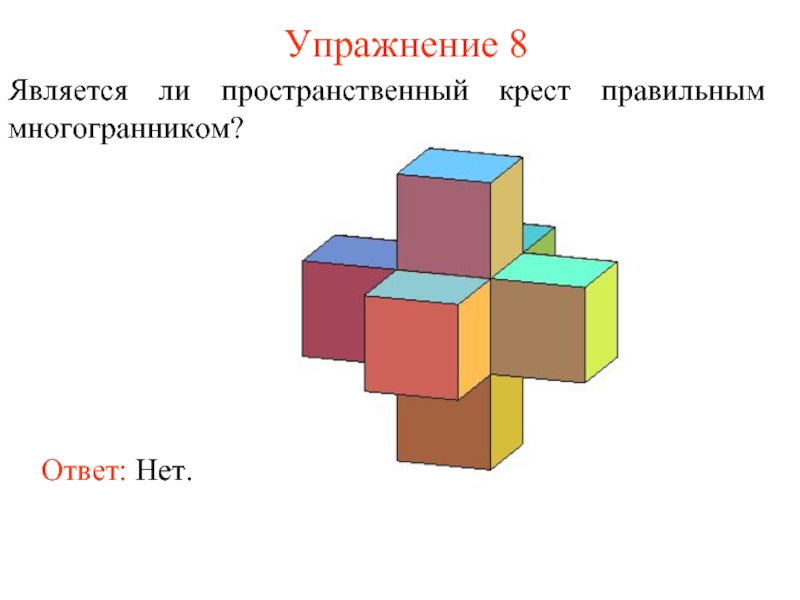
- 16. Упражнение 8 Является ли пространственный крест правильным многогранником? Ответ: Нет.
- 17. Упражнение 9 Сколько тетраэдров изображено на рисунке? Ответ: Пять.
- 18. Упражнение 10 Сколько кубов изображено на рисунке? Ответ: Три.
- 19. Упражнение 11 Сколько октаэдров изображено на рисунке? Ответ: Три.
- 20. Упражнение 12 Соединение каких двух многогранников изображено на рисунке? Ответ: Икосаэдра и додекаэдра.
- 21. Упражнение 13 Сколько вершин (В), ребер (Р)
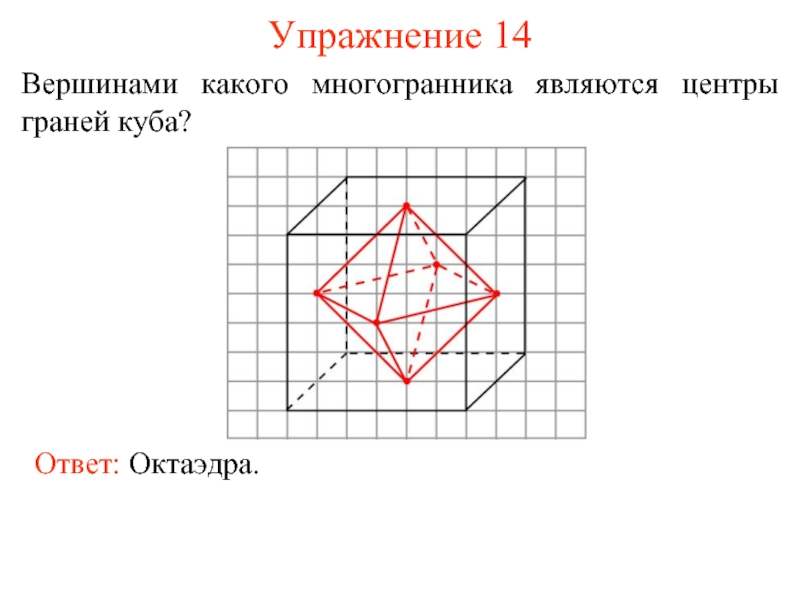
- 22. Упражнение 14 Вершинами какого многогранника являются центры граней куба?
- 23. Упражнение 15 Вершинами какого многогранника являются центры граней октаэдра?
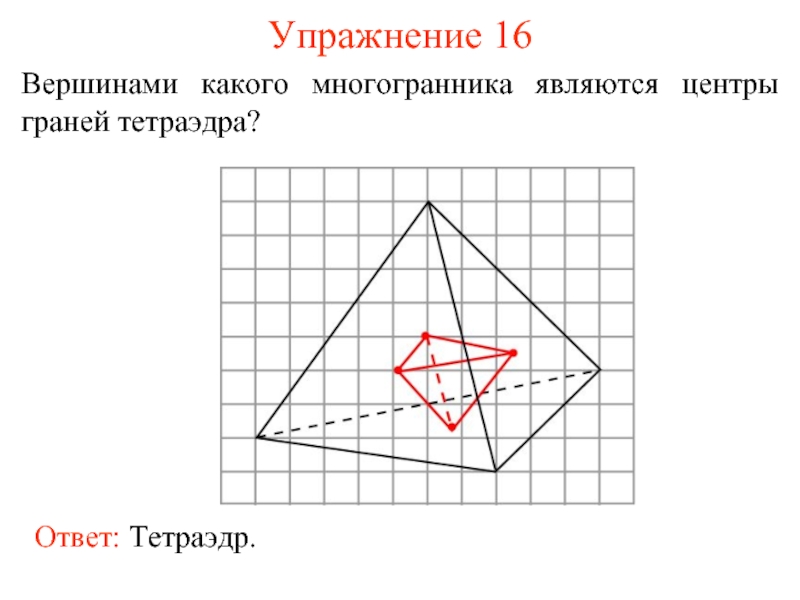
- 24. Упражнение 16 Вершинами какого многогранника являются центры граней тетраэдра?
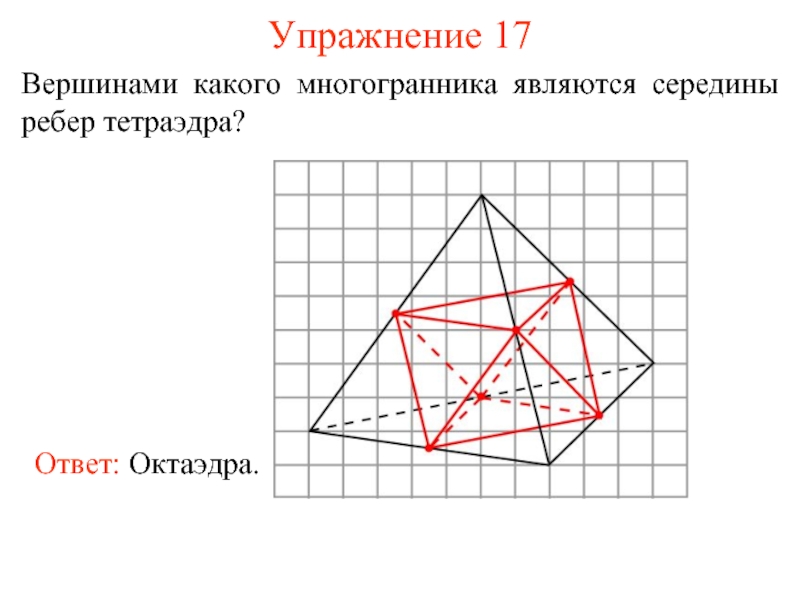
- 25. Упражнение 17 Вершинами какого многогранника являются середины ребер тетраэдра?
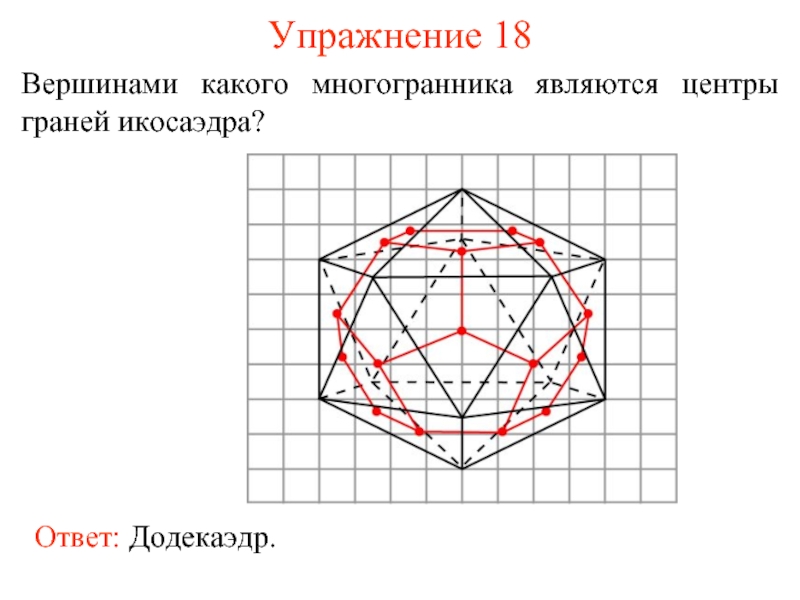
- 26. Упражнение 18 Вершинами какого многогранника являются центры граней икосаэдра?
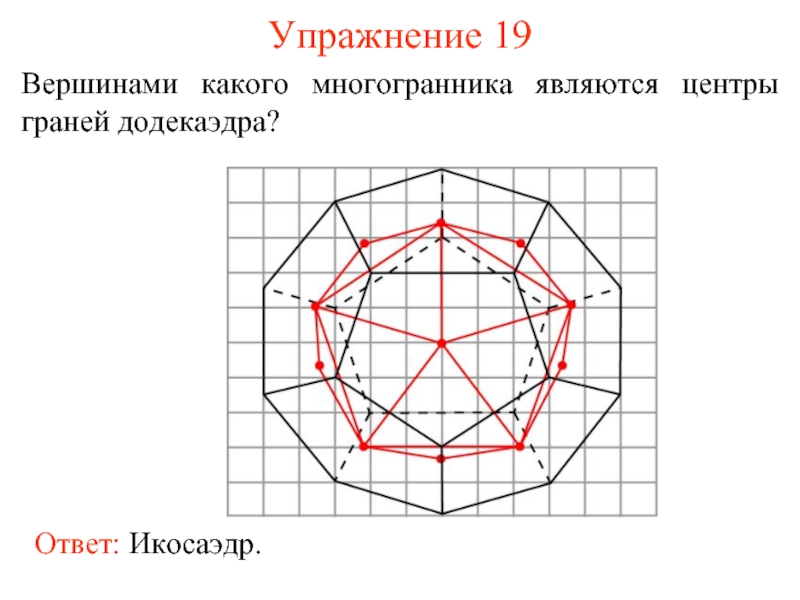
- 27. Упражнение 19 Вершинами какого многогранника являются центры граней додекаэдра?
- 28. Двойственные многогранники Два правильных многогранника называются двойственными,
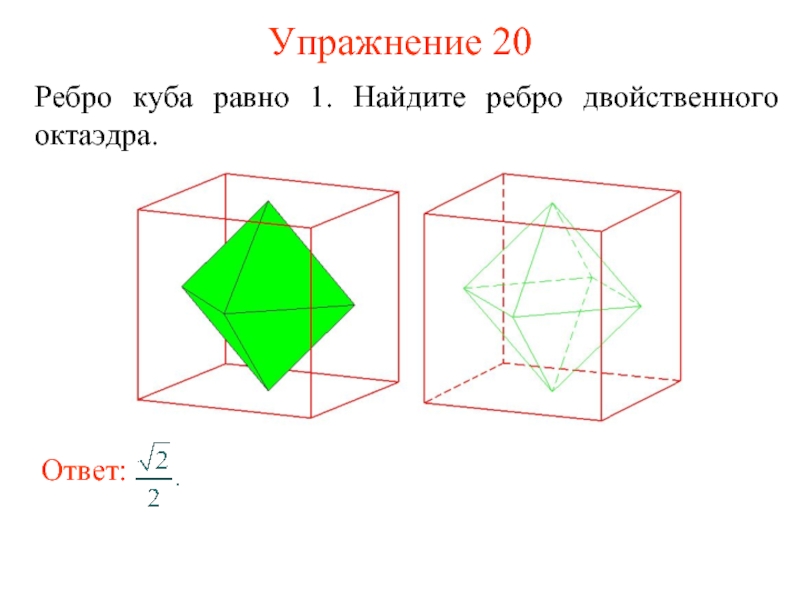
- 29. Упражнение 20 Ребро куба равно 1. Найдите ребро двойственного октаэдра.
- 30. Октаэдр и куб Центры граней октаэдра являются вершинами куба.
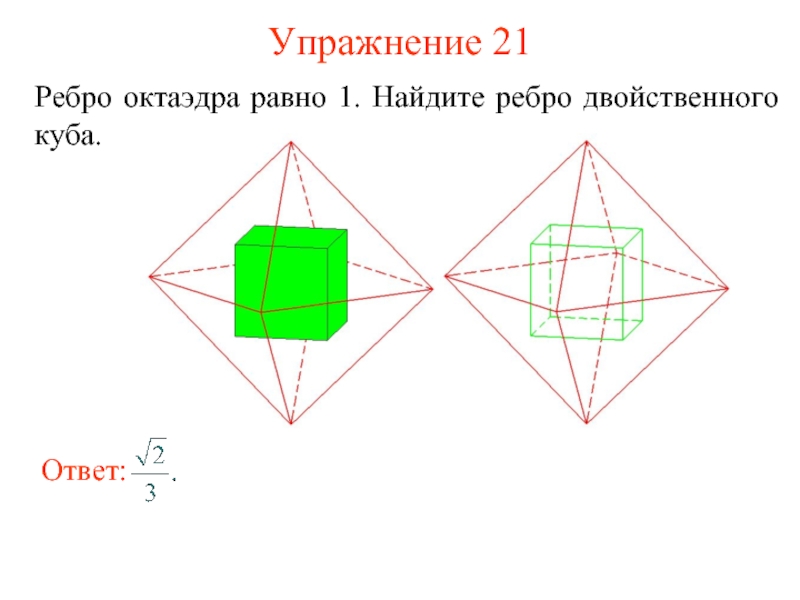
- 31. Упражнение 21 Ребро октаэдра равно 1. Найдите ребро двойственного куба.
- 32. Тетраэдр и тетраэдр Тетраэдр двойственен сам себе. Центры его граней являются вершинами тетраэдра.
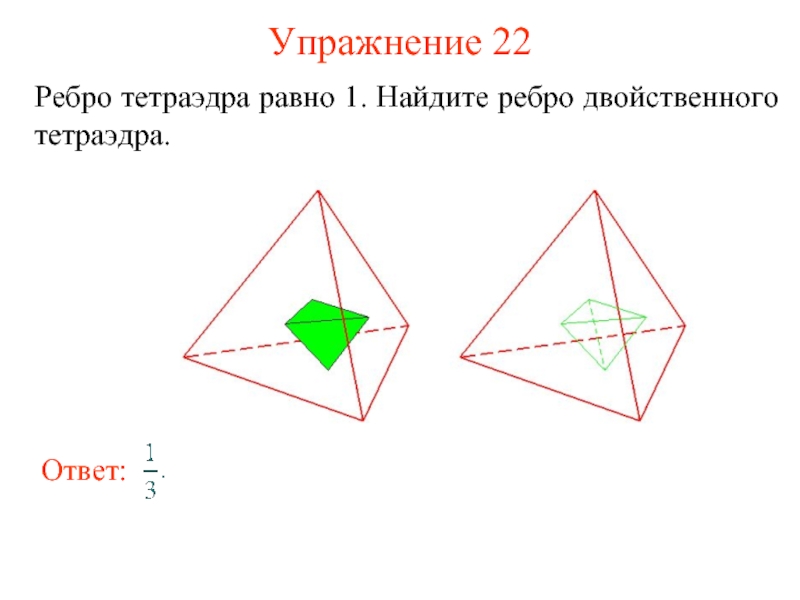
- 33. Упражнение 22 Ребро тетраэдра равно 1. Найдите ребро двойственного тетраэдра.
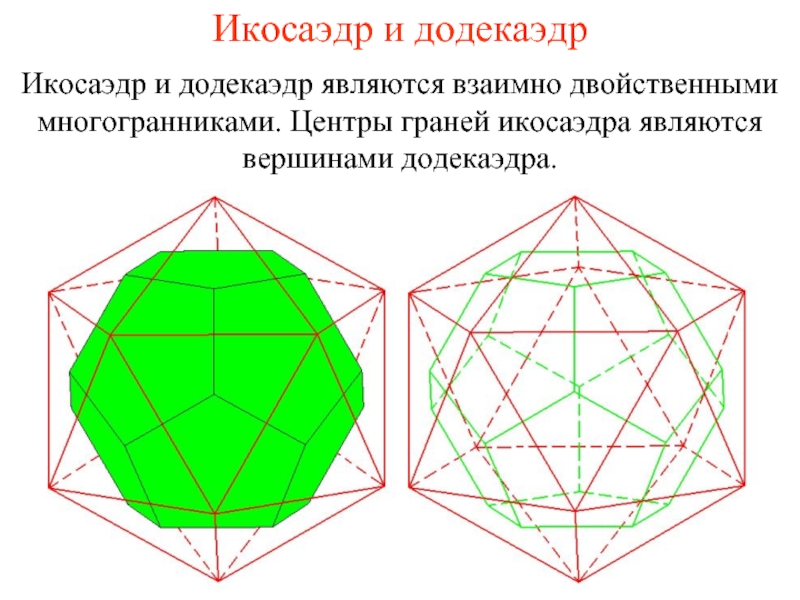
- 34. Икосаэдр и додекаэдр Икосаэдр и додекаэдр являются
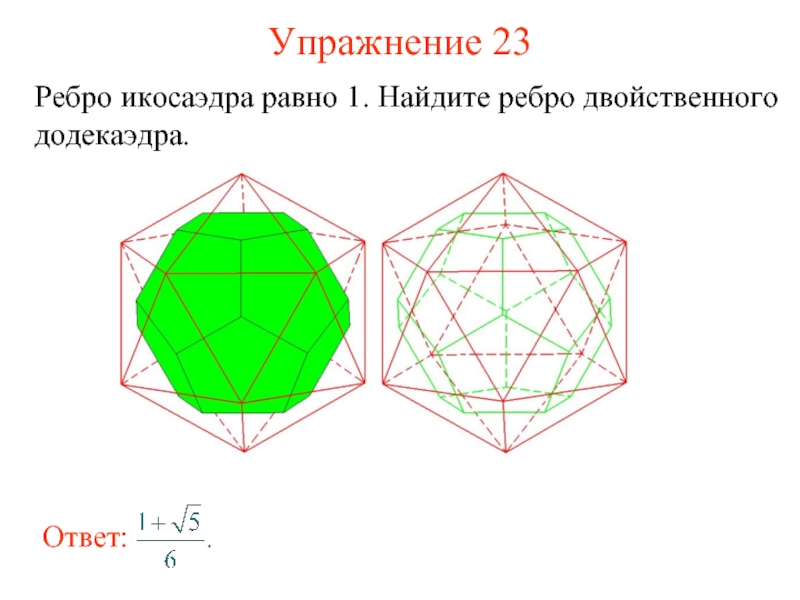
- 35. Упражнение 23 Ребро икосаэдра равно 1. Найдите ребро двойственного додекаэдра.
- 36. Додекаэдр и икосаэдр Центры граней додекаэдра являются вершинами икосаэдра.
- 37. Упражнение 24 Ребро додекаэдра равно 1. Найдите ребро двойственного икосаэдра.
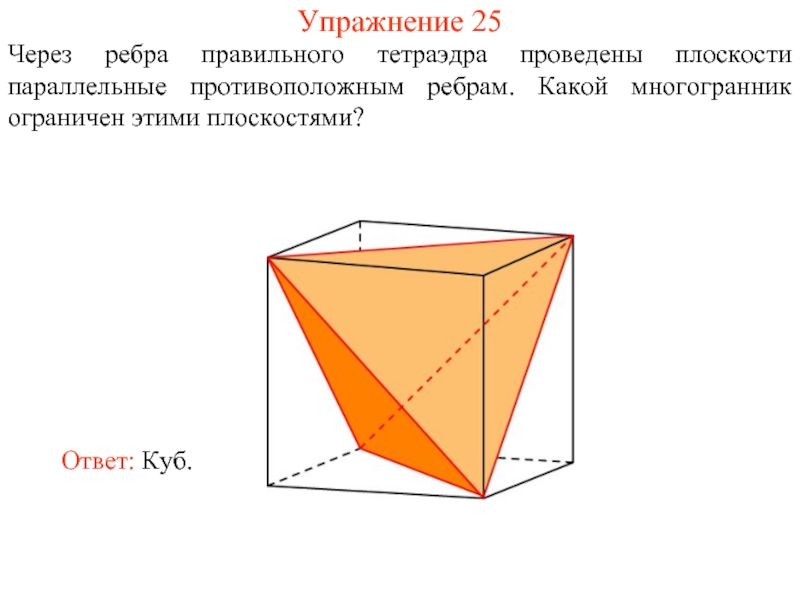
- 38. Упражнение 25 Через ребра правильного тетраэдра проведены
- 39. Упражнение 26 Через середины двух ребер куба,
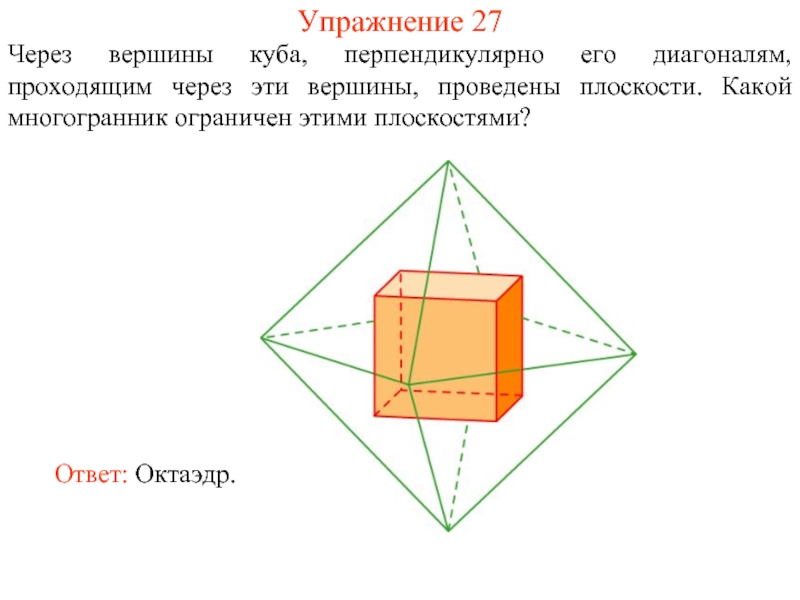
- 40. Упражнение 27 Через вершины куба, перпендикулярно его
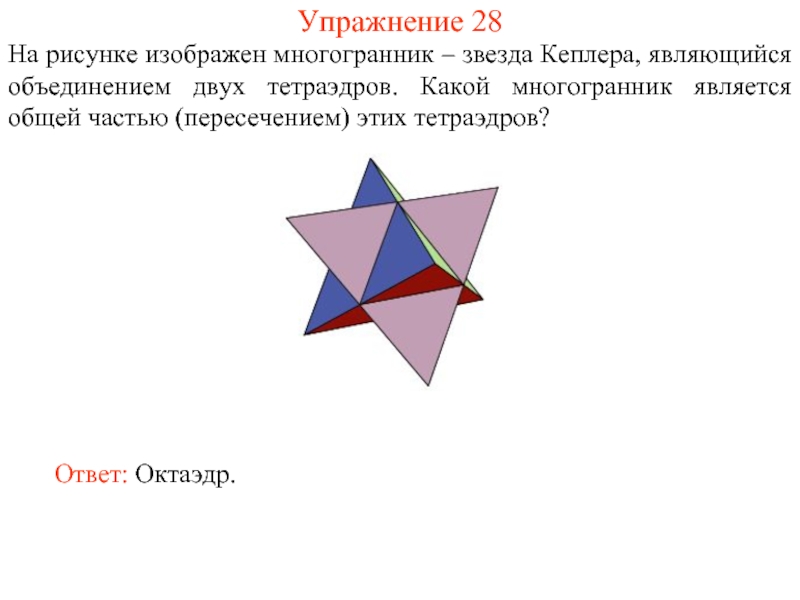
- 41. Упражнение 28 На рисунке изображен многогранник –
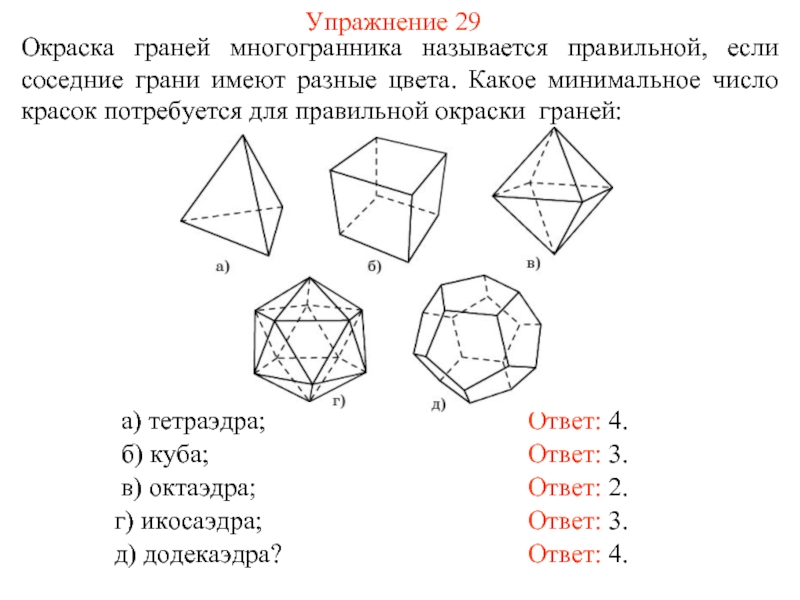
- 42. Упражнение 29 Окраска граней многогранника называется правильной,
Слайд 1ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Правильные многогранники были известны еще в древней Греции. Пифагор и
Слайд 2Кубок Кеплера
Иоганн Кеплер (1571 – 1630) в одной из первых
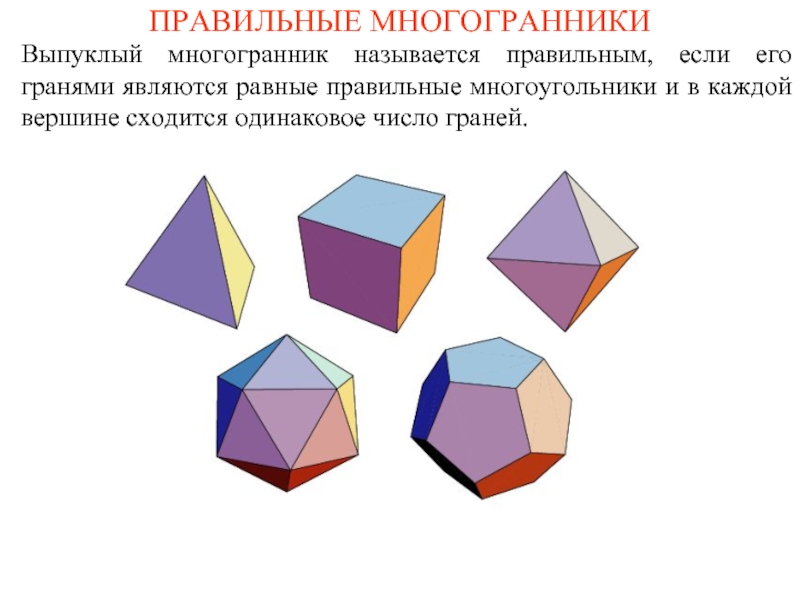
Слайд 3ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если его гранями являются равные правильные
Слайд 4ТЕТРАЭДР
Наиболее простым правильным многогранником является треугольная пирамида, грани которой правильные треугольники.
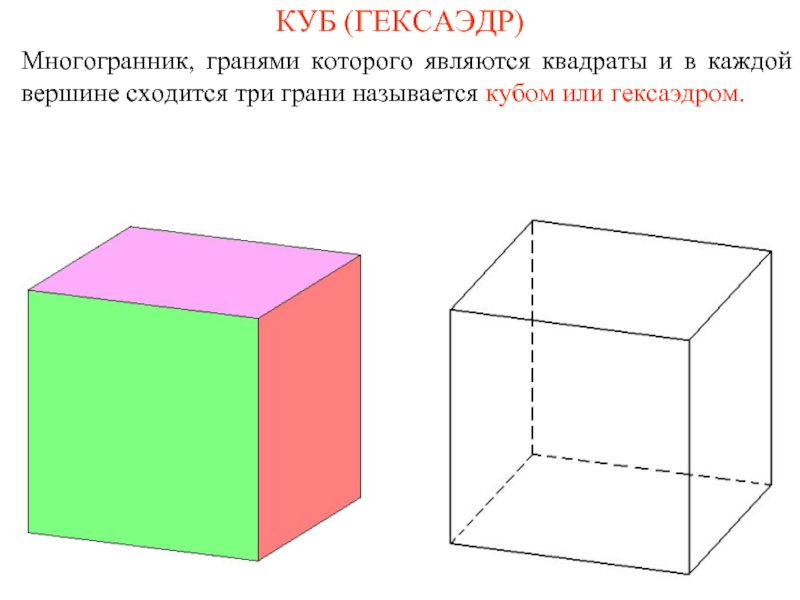
Слайд 6КУБ (ГЕКСАЭДР)
Многогранник, гранями которого являются квадраты и в каждой вершине сходится
Слайд 8ОКТАЭДР
Многогранник, гранями которого являются правильные треугольники и в каждой вершине сходится
Слайд 10ИКОСАЭДР
Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.
Слайд 12ДОДЕКАЭДР
Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходится
Слайд 14Упражнение 6
Почему гранями правильного многогранника не могут быть правильные шестиугольники?
Ответ: Потому
Слайд 15Упражнение 7
Представьте многогранник - бипирамиду, сложенную из двух равных правильных тетраэдров
Ответ: Нет, в его вершинах сходится разное число граней.
Слайд 20Упражнение 12
Соединение каких двух многогранников изображено на рисунке?
Ответ: Икосаэдра и додекаэдра.
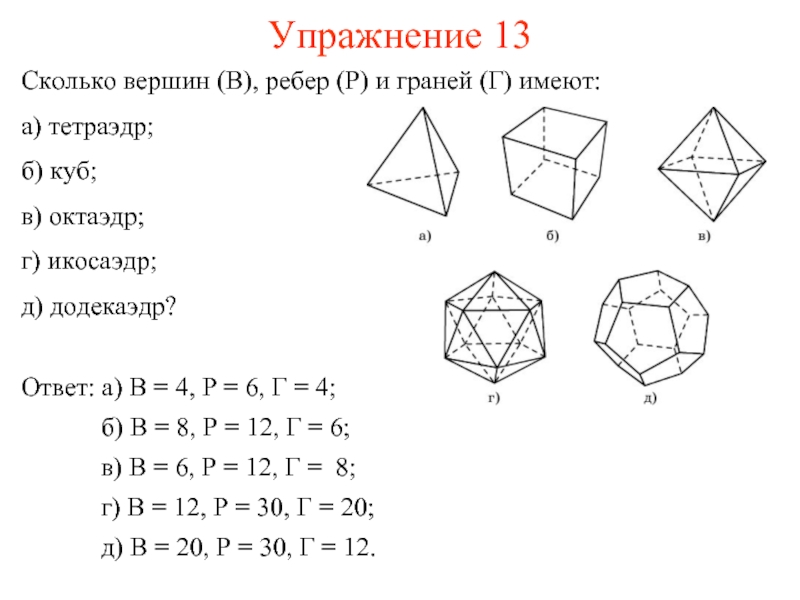
Слайд 21Упражнение 13
Сколько вершин (В), ребер (Р) и граней (Г) имеют:
а) тетраэдр;
б)
в) октаэдр;
г) икосаэдр;
д) додекаэдр?
Ответ: а) В = 4, Р = 6, Г = 4;
б) В = 8, Р = 12, Г = 6;
в) В = 6, Р = 12, Г = 8;
г) В = 12, Р = 30, Г = 20;
д) В = 20, Р = 30, Г = 12.
Слайд 28Двойственные многогранники
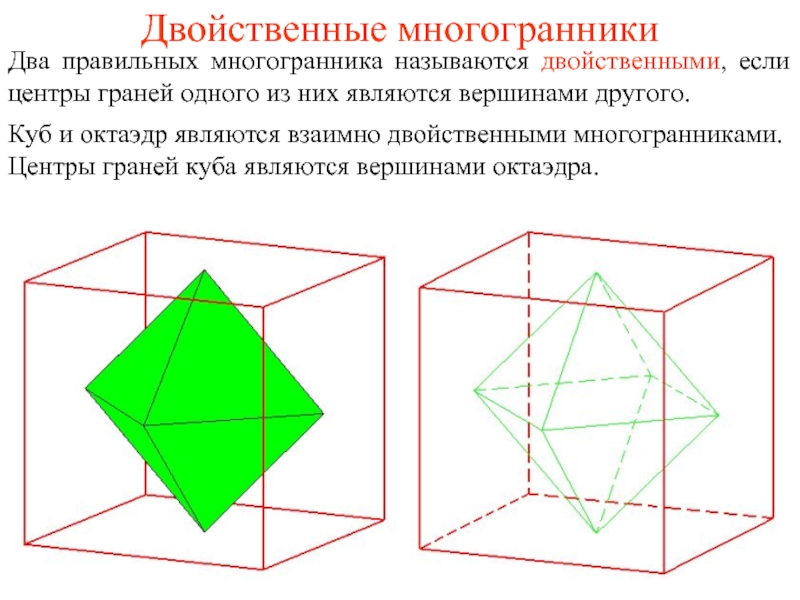
Два правильных многогранника называются двойственными, если центры граней одного из
Куб и октаэдр являются взаимно двойственными многогранниками. Центры граней куба являются вершинами октаэдра.
Слайд 32Тетраэдр и тетраэдр
Тетраэдр двойственен сам себе. Центры его граней являются вершинами
Слайд 34Икосаэдр и додекаэдр
Икосаэдр и додекаэдр являются взаимно двойственными многогранниками. Центры граней
Слайд 38Упражнение 25
Через ребра правильного тетраэдра проведены плоскости параллельные противоположным ребрам. Какой
Слайд 39Упражнение 26
Через середины двух ребер куба, выходящих из одной вершины, параллельно
Слайд 40Упражнение 27
Через вершины куба, перпендикулярно его диагоналям, проходящим через эти вершины,
Слайд 41Упражнение 28
На рисунке изображен многогранник – звезда Кеплера, являющийся объединением двух
Ответ: Октаэдр.
Слайд 42Упражнение 29
Окраска граней многогранника называется правильной, если соседние грани имеют разные
Ответ: 4.
а) тетраэдра;
б) куба;
в) октаэдра;
г) икосаэдра;
д) додекаэдра?
Ответ: 3.
Ответ: 2.
Ответ: 3.
Ответ: 4.