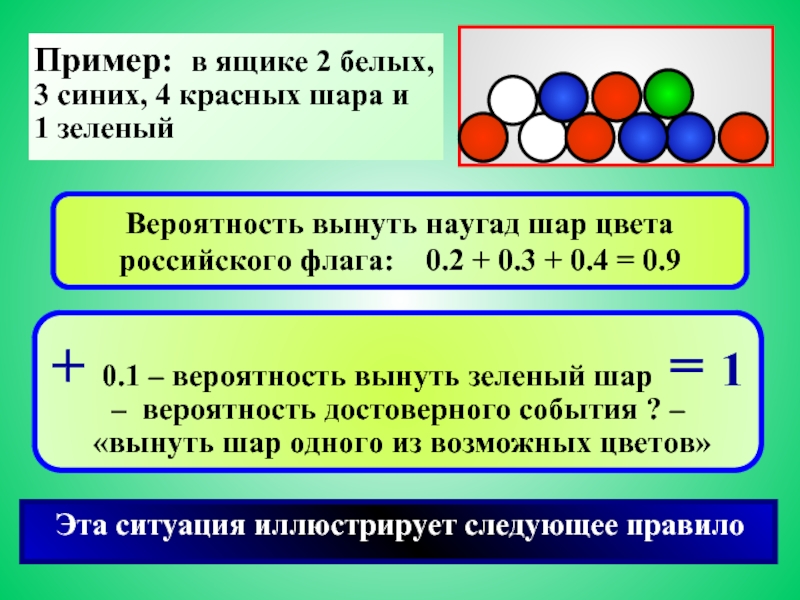
- правило сложения для несовместных событий
- сумма вероятностей событий полной группы
- вероятности противоположных событий
- зависимые и независимые события
- условная и безусловная вероятность
- правило умножения
- условие независимости
Ключевые слова