второго порядка.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности второго порядка презентация
Содержание
- 1. Поверхности второго порядка
- 2. Понятие поверхности второго порядка Определение.
- 3. Цилиндрические поверхности Определение. Цилиндрическими
- 4. Цилиндрические поверхности Рассмотрим поверхности, в
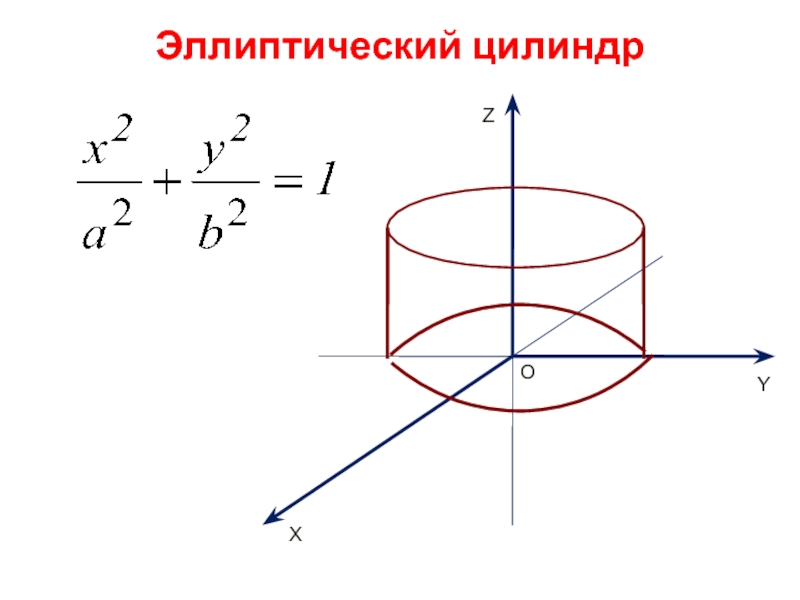
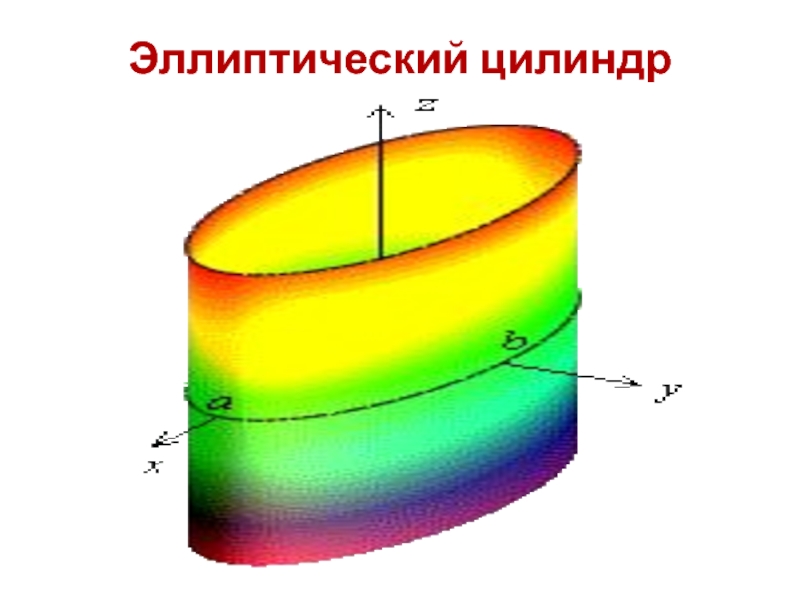
- 5. Эллиптический цилиндр - X Y Z O
- 6. Эллиптический цилиндр
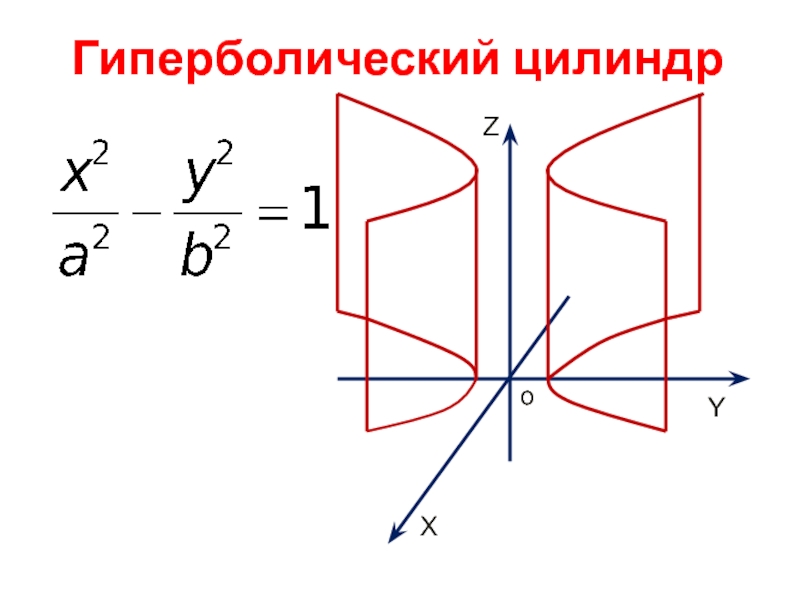
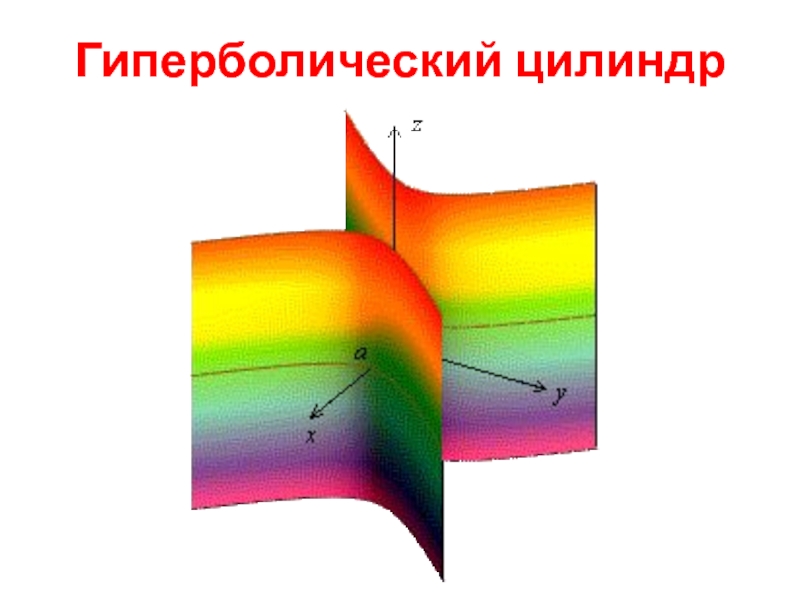
- 7. Гиперболический цилиндр X Y Z o
- 8. Гиперболический цилиндр
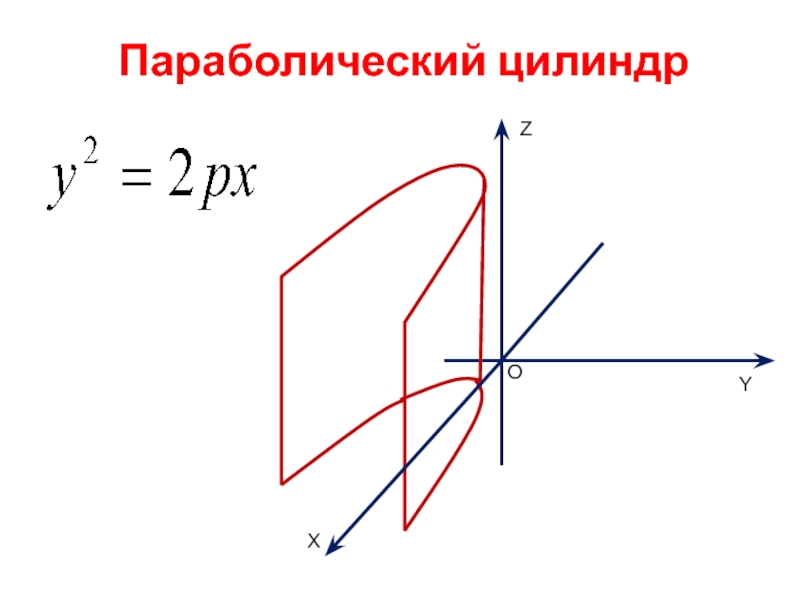
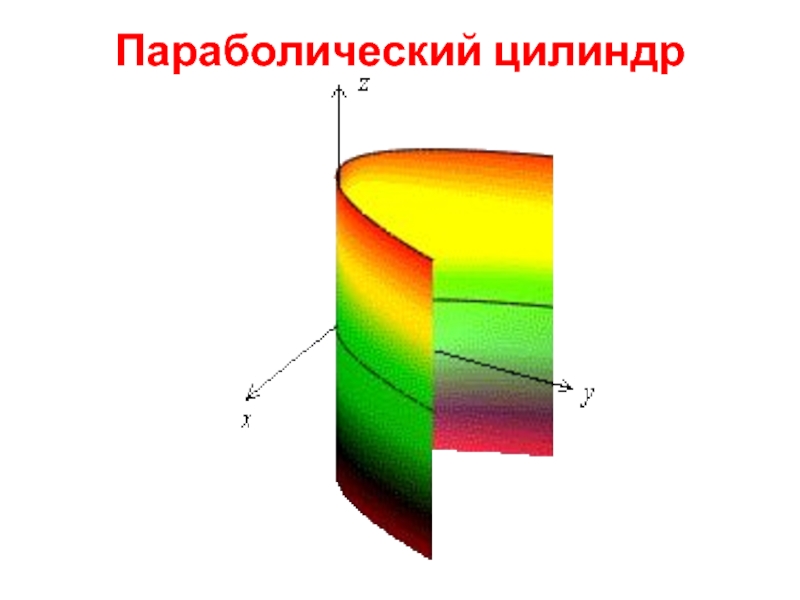
- 9. Параболический цилиндр X Y Z O
- 10. Параболический цилиндр
- 11. Поверхности вращения Определение. Поверхность, описываемая некоторой
- 12. Если уравнение поверхности в прямоугольной системе координат
- 13. Эллипсоид вращения
- 14. Однополостный гиперболоид вращения
- 15. Двуполостный гиперболоид вращения
- 16. Параболоид вращения
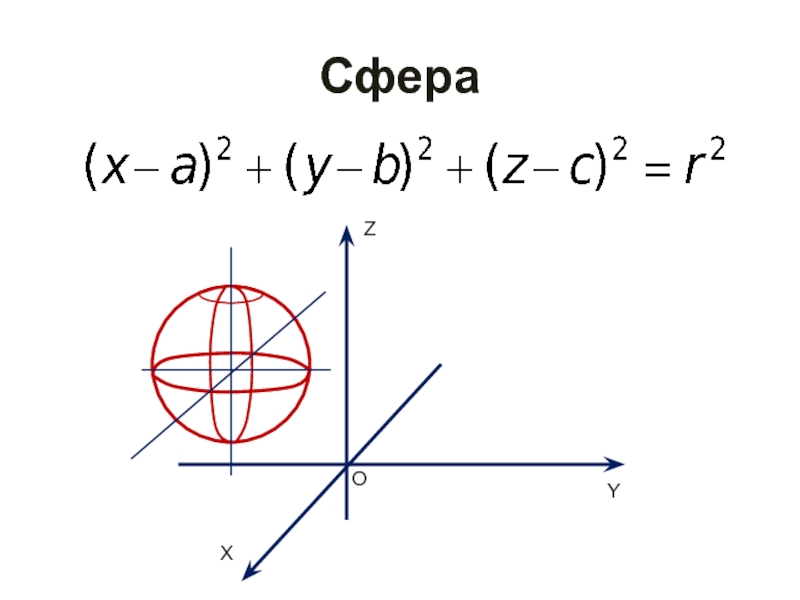
- 17. Сфера X Y Z O
- 18. Сфера
- 19. Трехосный эллипсоид
- 20. Эллипсоид В сечении эллипсоида плоскостями, параллельными координатным
- 21. Если две полуоси равны друг другу (
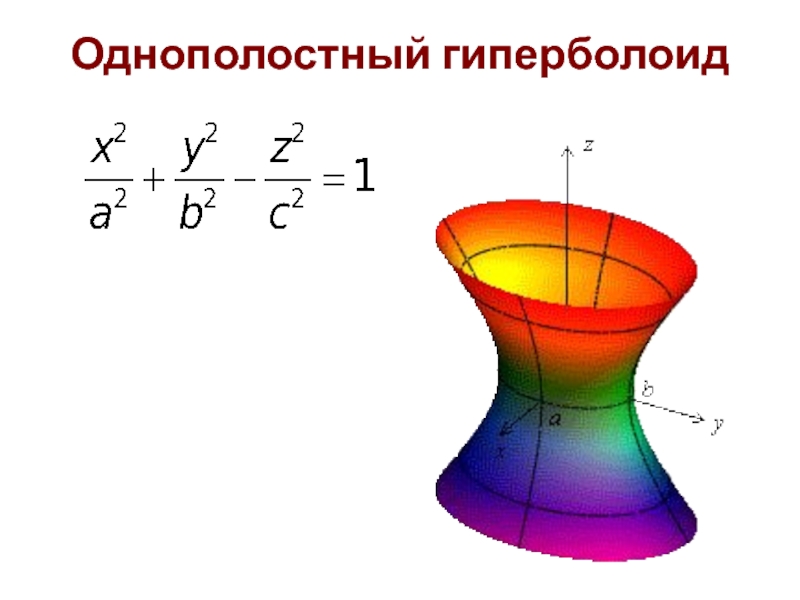
- 22. Однополостный гиперболоид
- 23. Однополостный гиперболоид
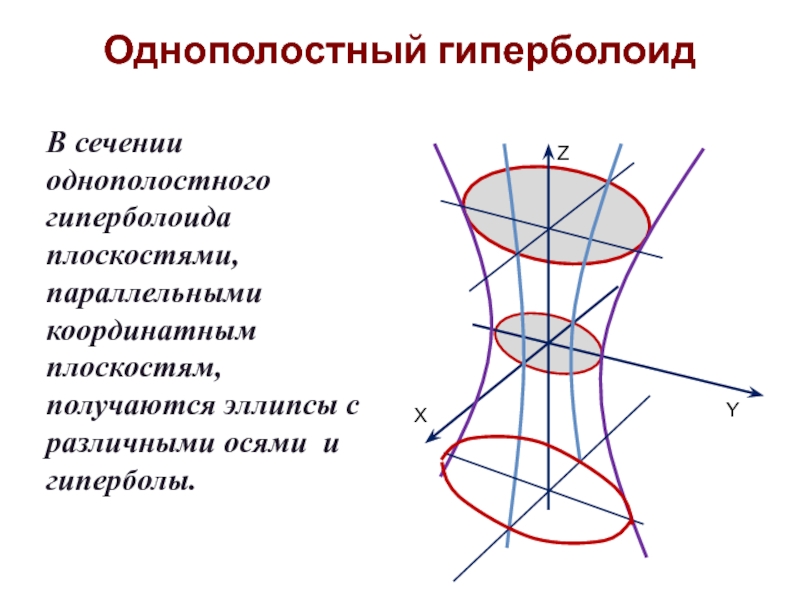
- 24. Однополостный гиперболоид В сечении однополостного гиперболоида
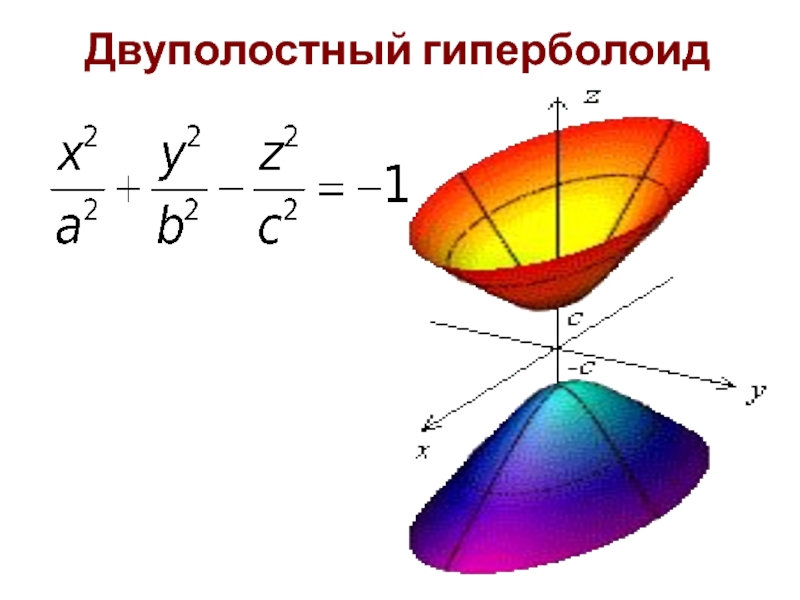
- 25. Двуполостный гиперболоид
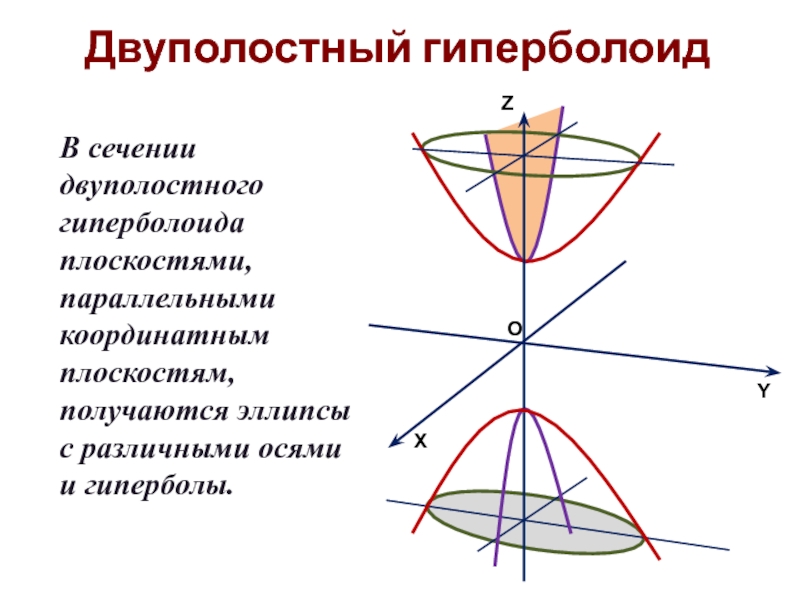
- 26. Двуполостный гиперболоид В сечении двуполостного
- 27. Двуполостный гиперболоид
- 28. Эллиптический параболоид
- 29. Эллиптический параболоид В сечении эллиптического параболоида
- 30. Эллиптический параболоид
- 31. Гиперболический параболоид
- 32. Гиперболический параболоид В сечении гиперболического параболоида
- 33. Конус второго порядка
- 34. Конус второго порядка В сечении конуса
- 35. Пример. В плоскости Oyz дано уравнение линии
- 36. Пример. В плоскости Oyz дано уравнение линии
Слайд 1Поверхности второго порядка
План
Понятие поверхности второго порядка.
Цилиндрические поверхности.
Эллипсоид.
Однополостный гиперболоид.
Двуполостный гиперболоид.
Эллиптический параболоид.
Гиперболический параболоид.
Конус
Слайд 2
Понятие поверхности второго порядка
Определение.
Поверхностью второго порядка называется поверхность в прямоугольной
системе координат, определяемая алгебраическим уравнением второй степени.
Слайд 3
Цилиндрические поверхности
Определение.
Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой -
либо фиксированной прямой.
Слайд 4
Цилиндрические поверхности
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие
параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих.
Слайд 11Поверхности вращения
Определение.
Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d,
называется поверхностью вращения с осью вращения d.
Слайд 12Если уравнение поверхности в прямоугольной системе координат имеет вид: F(x2 +
y2, z) = 0, то эта поверхность вращения с осью вращения Оz.
Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу,
F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох.
Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу,
F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох.
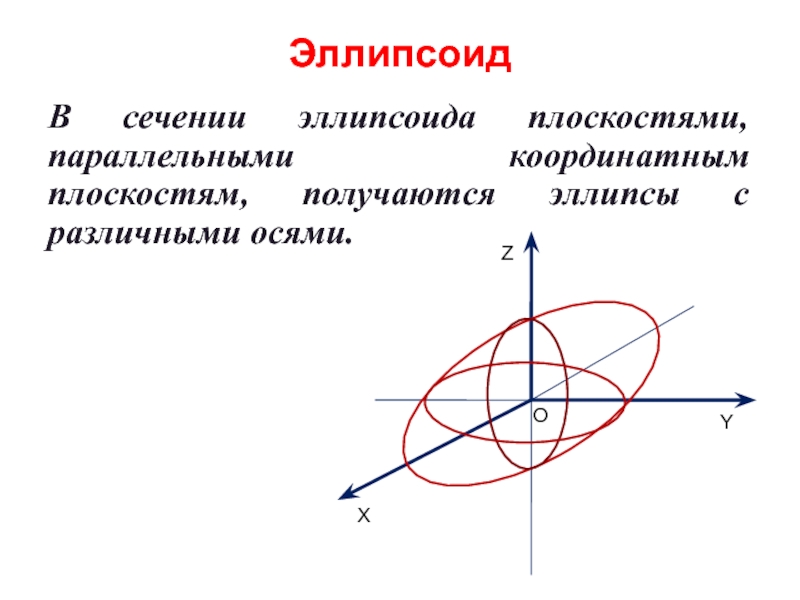
Слайд 20Эллипсоид
В сечении эллипсоида плоскостями, параллельными координатным плоскостям, получаются эллипсы с различными
осями.
X
Y
Z
O
Слайд 21Если две полуоси равны друг другу (
),
то эллипсоид называется эллипсоидом вращения.
Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.
Сам эллипсоид может быть получен из эллипса
лежащего в плоскости, при
вращении его вокруг оси
то эллипсоид называется эллипсоидом вращения.
Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.
Сам эллипсоид может быть получен из эллипса
лежащего в плоскости, при
вращении его вокруг оси
Слайд 24Однополостный гиперболоид
В сечении однополостного гиперболоида плоскостями, параллельными координатным плоскостям, получаются
эллипсы с различными осями и гиперболы.
Y
X
Z
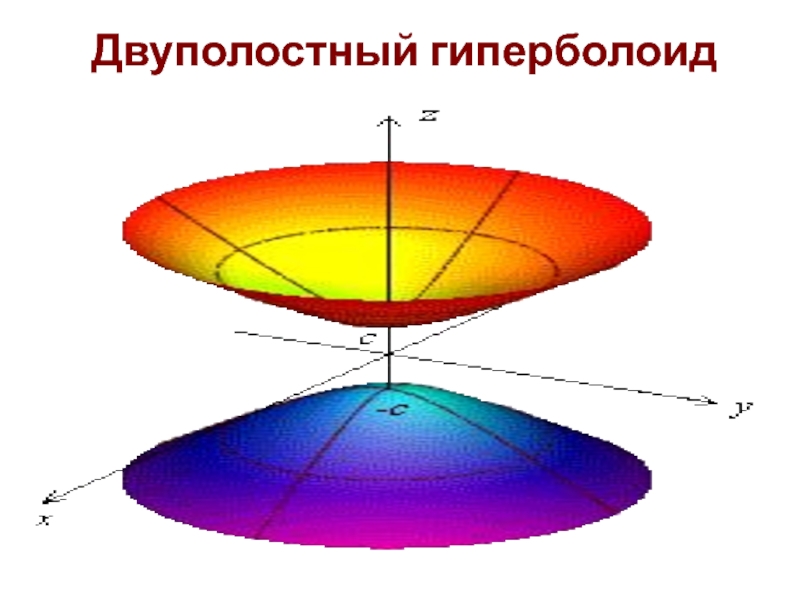
Слайд 26Двуполостный гиперболоид
В сечении двуполостного гиперболоида плоскостями, параллельными координатным плоскостям, получаются
эллипсы с различными осями и гиперболы.
X
Y
Z
O
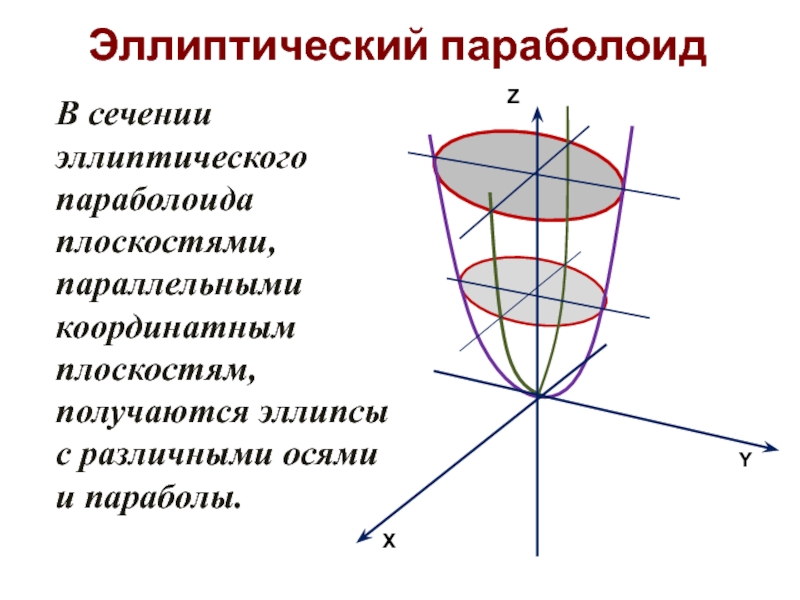
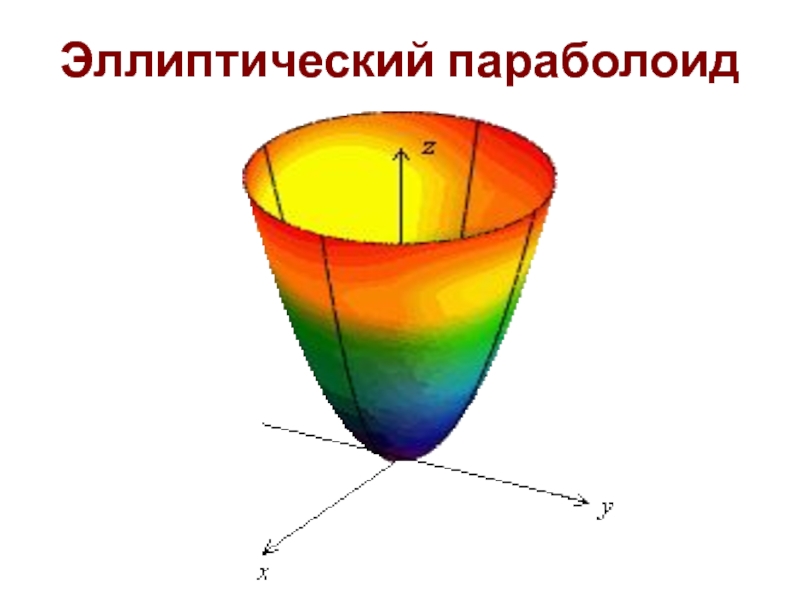
Слайд 29Эллиптический параболоид
В сечении эллиптического параболоида плоскостями, параллельными координатным плоскостям, получаются
эллипсы с различными осями и параболы.
X
Y
Z
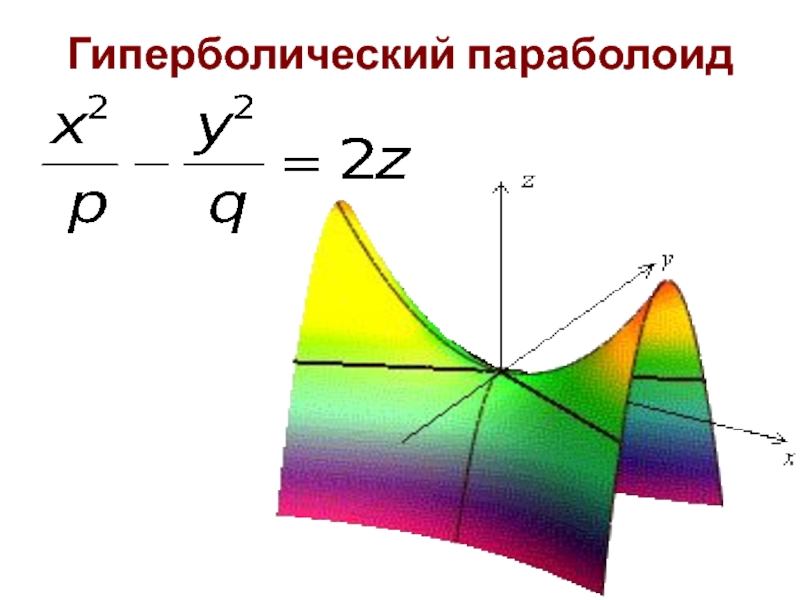
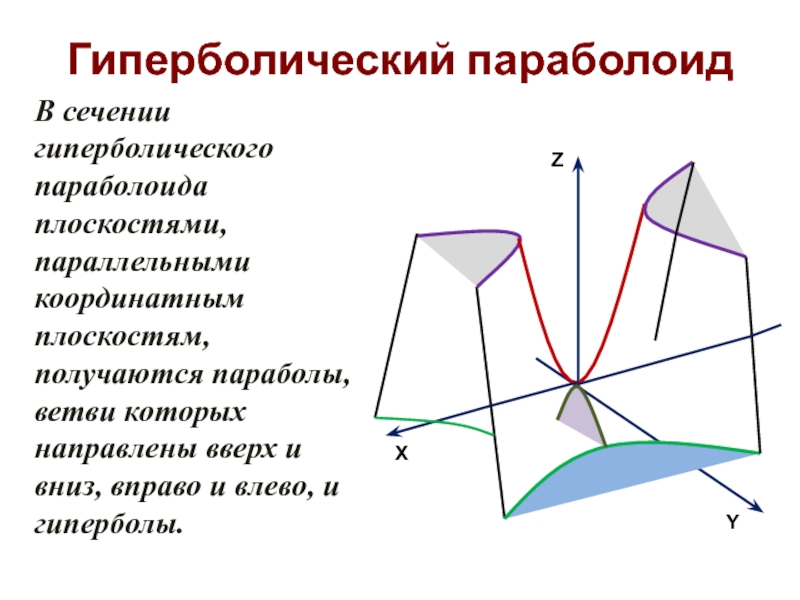
Слайд 32Гиперболический параболоид
В сечении гиперболического параболоида плоскостями, параллельными координатным плоскостям, получаются
параболы, ветви которых направлены вверх и вниз, вправо и влево, и гиперболы.
X
Y
Z
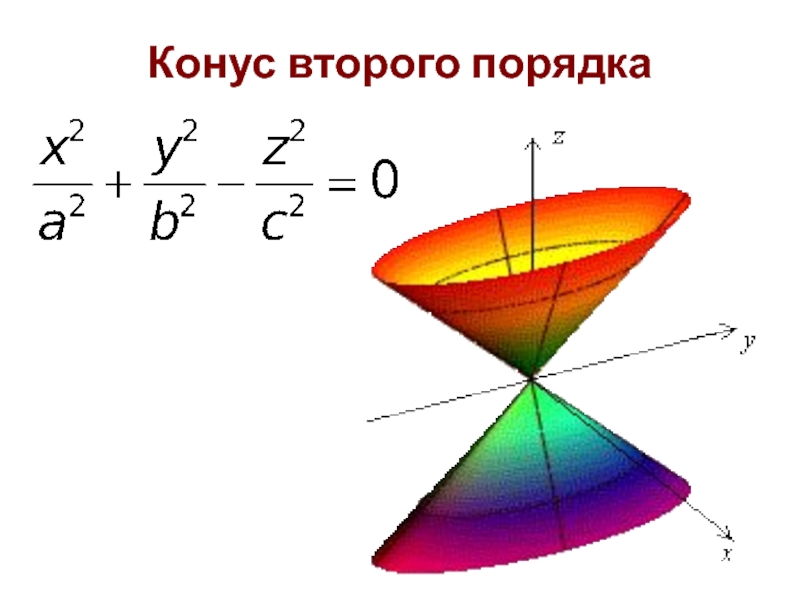
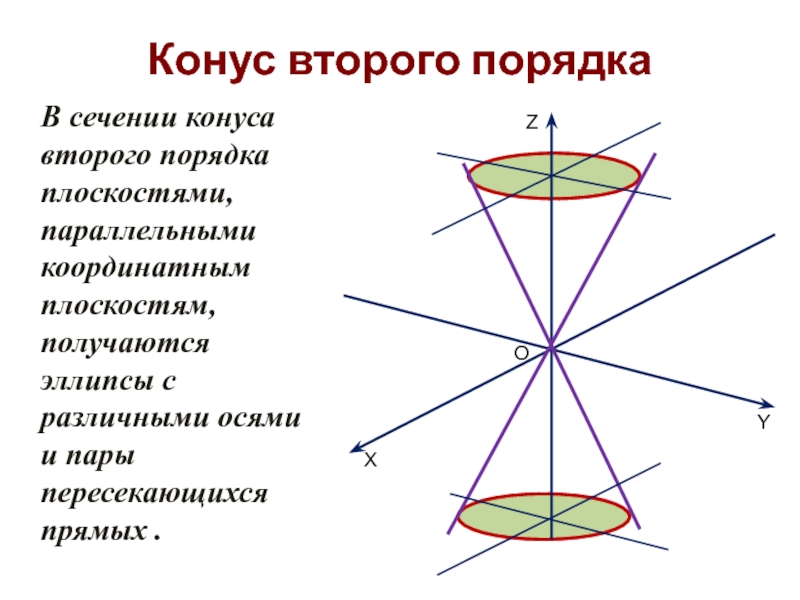
Слайд 34Конус второго порядка
В сечении конуса второго порядка плоскостями, параллельными координатным
плоскостям, получаются эллипсы с различными осями и пары пересекающихся прямых .
X
Y
Z
O
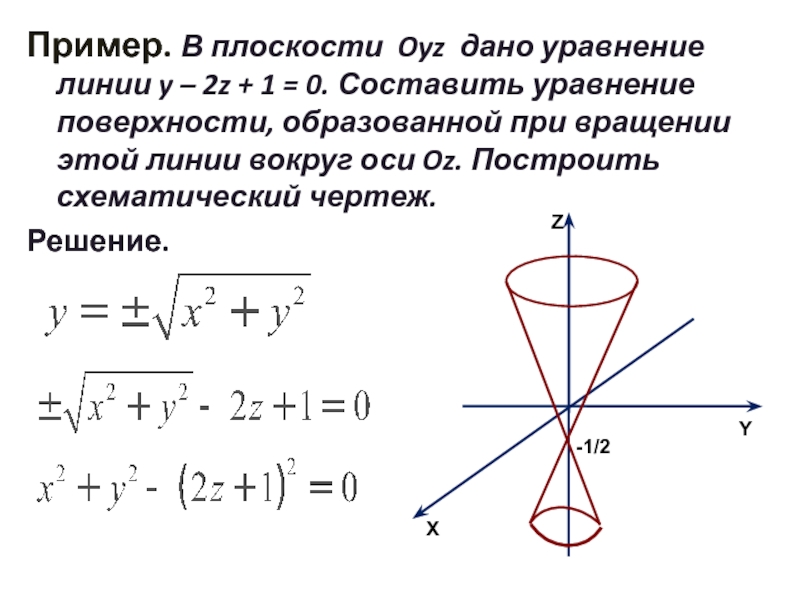
Слайд 35Пример. В плоскости Oyz дано уравнение линии y – 2z +
1 = 0. Составить уравнение поверхности, образованной при вращении этой линии вокруг оси Oz. Построить схематический чертеж.
Решение.
Решение.
X
Y
Z
-1/2
Слайд 36Пример. В плоскости Oyz дано уравнение линии y – z2 –
2 = 0. Составить уравнение поверхности, образованной вращением этой линии вокруг оси Oy. Построить схематический чертеж.
Решение.
Решение.
X
Y
Z
O
2
