- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности второго порядка презентация
Содержание
- 1. Поверхности второго порядка
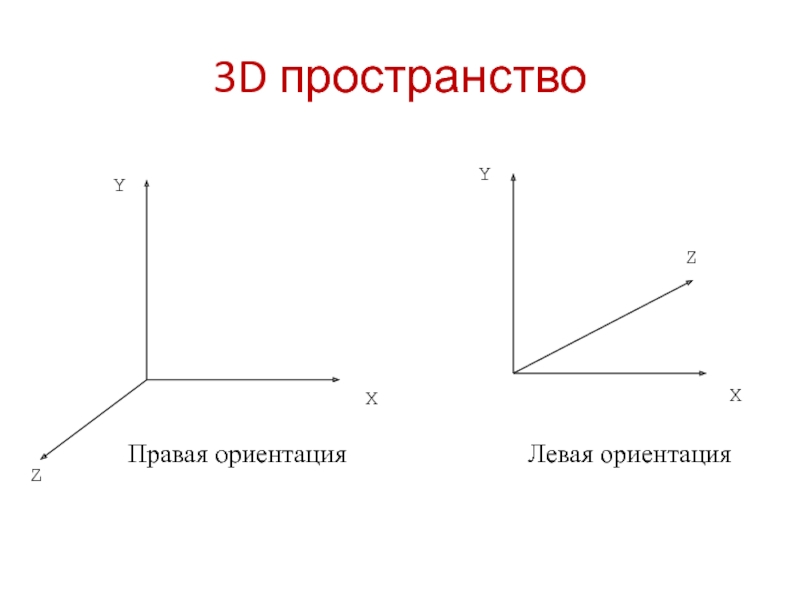
- 2. 3D пространство Y Z X Y Z X Правая ориентация Левая ориентация
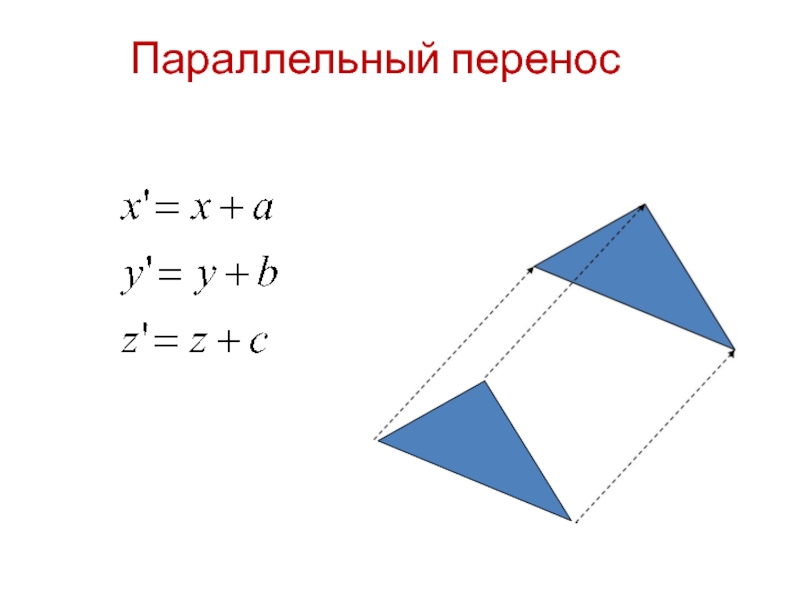
- 3. Параллельный перенос
- 4. Параллельный перенос
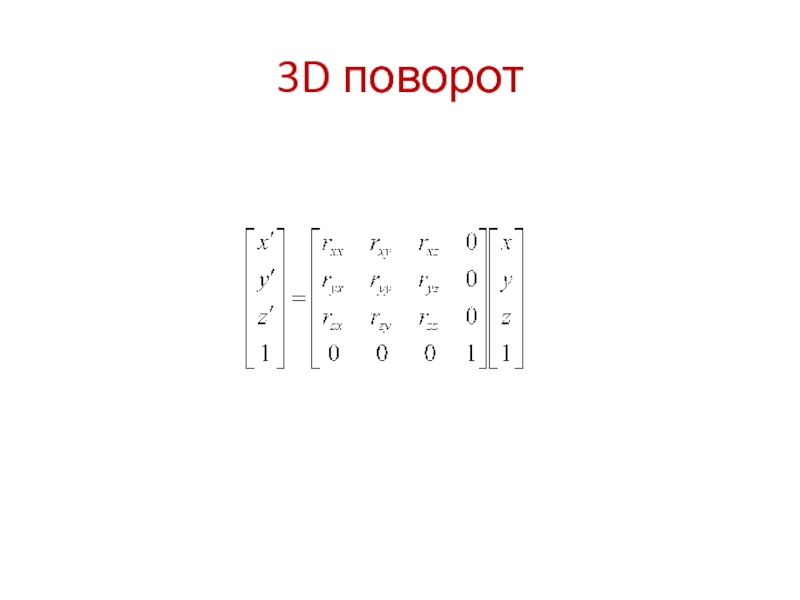
- 5. 3D поворот Рассматривается поворот осей координат вокруг
- 6. 3D поворот
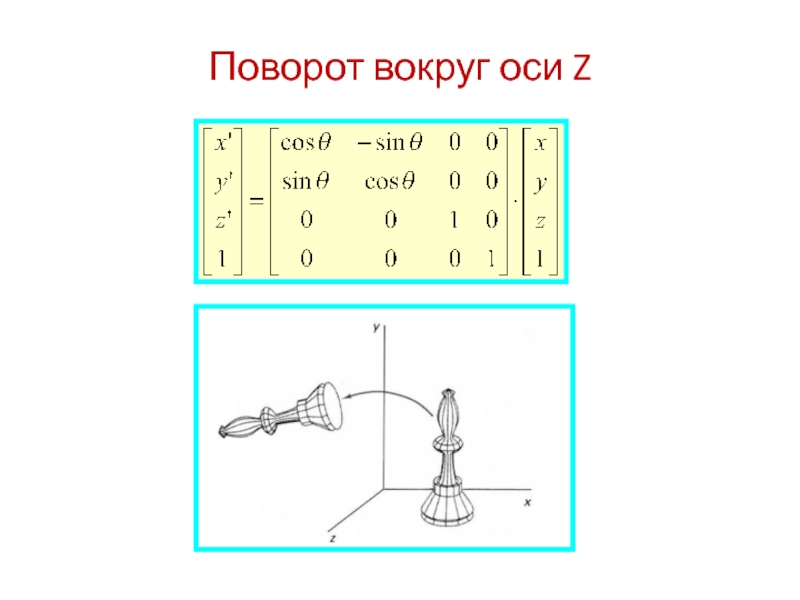
- 7. Поворот вокруг оси Z
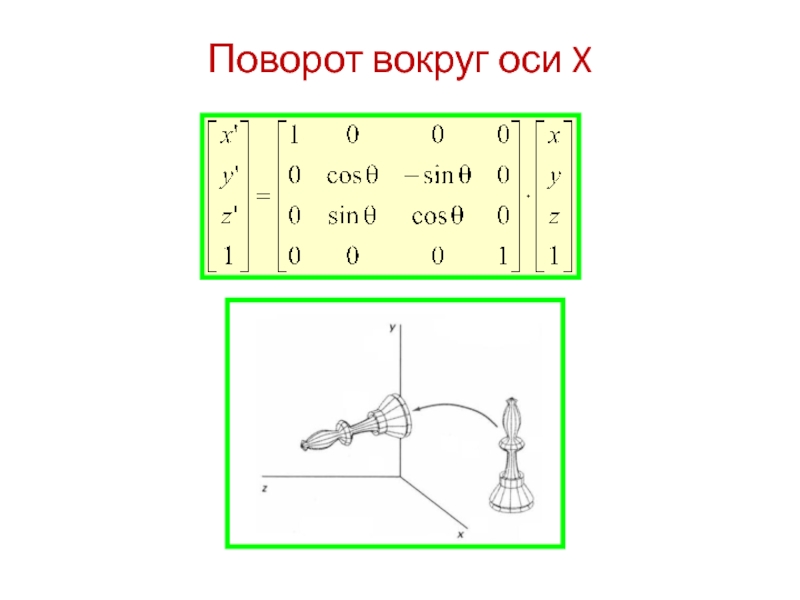
- 8. Поворот вокруг оси X
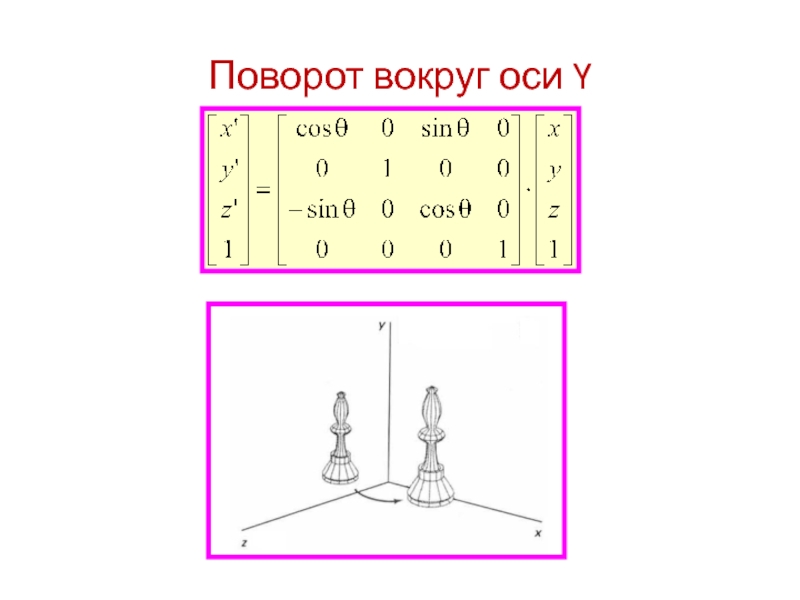
- 9. Поворот вокруг оси Y
- 10. Уравнение поверхности 2-го порядка
- 11. Составим матрицу Так как
- 12. 1. Все собственные числа отличны от
- 13. 1. Все собственные числа отличны от
- 14. 1. Все собственные числа отличны от
- 15. 1. Все собственные числа отличны от
- 16. Эллипсоид Каноническое уравнение трехосного эллипсоида имеет вид
- 17. 1. Все собственные числа отличны от
- 18. Конусы 2-го порядка Каноническое уравнение конуса
- 19. Конусы с разными осями симметрии Ось симметрии
- 20. 1. Все собственные числа отличны от
- 21. Гиперболоиды Канонические уравнения гиперболоидов Каноническое
- 22. Разные ориентации однополостных гиперболоидов Ориентация
- 23. Гиперболоиды Каноническое уравнение двуполостного гиперболоида
- 24. Разные ориентации двуполостного гиперболоида Каноническое
- 25. 2. Одно из собственных чисел равно
- 26. 2. Одно из собственных чисел равно
- 27. 2. Одно из собственных чисел равно
- 28. Эллиптические цилиндры ось симметрии
- 29. 2. Одно из собственных чисел равно
- 30. Гиперболические цилиндры ось симметрии
- 31. 2. Одно из собственных чисел равно
- 32. 2. Одно из собственных чисел равно
- 33. Параболоиды Канонические уравнения параболоидов можно записать в
- 34. Гиперболический параболоид Каноническое уравнение гиперболического параболоида имеет
- 35. 3. Два собственных числа равны нулю
- 36. 3. Два собственных числа равны нулю
- 37. 3. Два собственных числа равны нулю
- 38. Параболические цилиндры
Слайд 53D поворот
Рассматривается поворот осей координат вокруг начала координат.
В матричном представлении: всякая
Строки и столбцы образуют ортонормированную систему
Определитель равен +1 или -1
Обратная матрица совпадает с транспонированной.
Слайд 10Уравнение поверхности 2-го порядка
Уравнение поверхности 2-го порядка
главная(квадратичная) часть
линейная
.
Основная задача состоит в умении по уравнению определить тип
поверхности, привести само уравнение к каноническому виду и
построить поверхность в системе координат. Сначала произведем
поворот системы координат.
Слайд 11Составим матрицу
Так как матрица симметрическая, то существует ортогональное преобразование (поворот),
приводящее
Хотя бы один из коэффициентов при квадратах отличен от нуля, иначе матрица A была бы нулевой. Рассмотрим три случая.
Слайд 121. Все собственные числа отличны от нуля.
Выделим полные квадраты
выполним параллельный
получим
Слайд 131. Все собственные числа отличны от нуля.
1.1. Если знаки
Получим каноническое уравнение точки (вырожденный эллипсоид)
Слайд 141. Все собственные числа отличны от нуля.
1.2. Если знаки
Получим каноническое уравнение мнимого эллипсоида
Слайд 151. Все собственные числа отличны от нуля.
1.3. Если знаки
Получим каноническое уравнение действительного эллипсоида
Слайд 16Эллипсоид
Каноническое уравнение трехосного эллипсоида имеет вид
a
b
c
полуоси
Центр этого эллипсоида находится
в начале координат.
Признаки уравнения эллипсоида:
Наличие квадратов всех трех переменных
Одинаковые знаки при квадратах переменных
Слайд 171. Все собственные числа отличны от нуля.
1.4. Знаки
Получим каноническое уравнение конуса
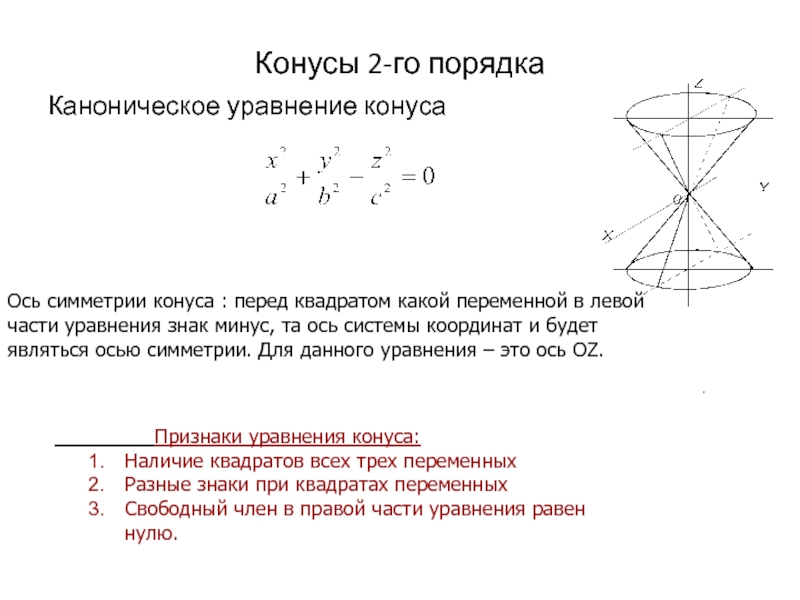
Слайд 18Конусы 2-го порядка
Каноническое уравнение конуса
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Свободный член в правой части уравнения равен нулю.
Ось симметрии конуса : перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии. Для данного уравнения – это ось OZ.
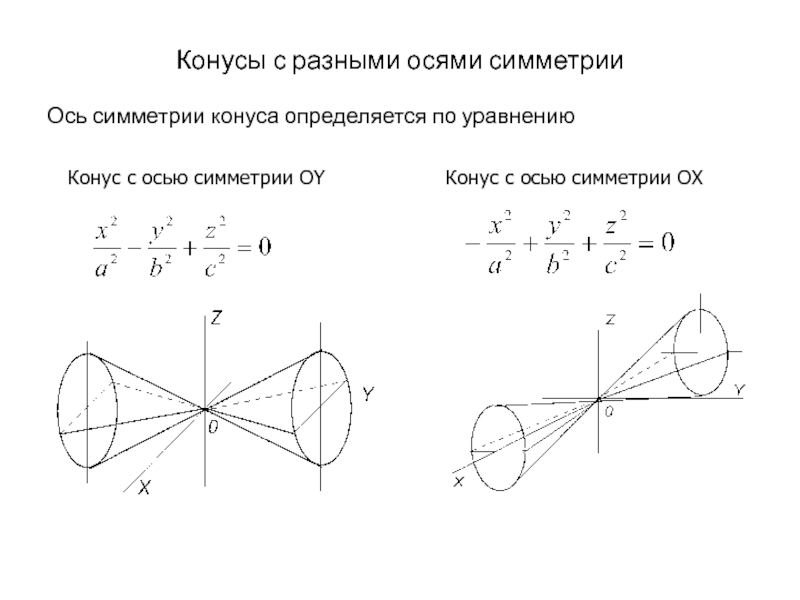
Слайд 19Конусы с разными осями симметрии
Ось симметрии конуса определяется по уравнению
Конус с
Конус с осью симметрии OX
Слайд 201. Все собственные числа отличны от нуля.
1.5. Знаки
Получим каноническое уравнение гиперболоида
Слайд 21Гиперболоиды
Канонические уравнения гиперболоидов
Каноническое уравнение однополостного
гиперболоида
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Один знак минус при квадрате переменной в левой части уравнения,
в правой части плюс 1.
полуоси
В зависимости от знака перед единицей в правой части гиперболоиды делятся на одно и двуполостные.
Слайд 22Разные ориентации однополостных гиперболоидов
Ориентация гиперболоида зависит от того, перед
Однополостный гиперболоид
с осью симметрии OY
Однополостный гиперболоид
с осью симметрии OX
Слайд 23Гиперболоиды
Каноническое уравнение двуполостного гиперболоида
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Два знака минус в уравнении: один при квадрате переменной
в левой части уравнения, другой в правой части при 1.
полуоси
Если из уравнения выразить z, то получим
Т.к.
, то получается, что
Двуполостный гиперболоид на проходит через начало координат.
Слайд 24Разные ориентации двуполостного гиперболоида
Каноническое уравнение двуполостного гиперболоида содержит два
Один знак минус оставляем в левой части уравнения, а второй поставим перед единицей в правой части. В таком случае легко определить ось симметрии гиперболоида: перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии.
Слайд 252. Одно из собственных чисел равно нулю (
Выделим полные квадраты
2.1. , выполним параллельный перенос
получим
Слайд 262. Одно из собственных чисел равно нулю (
2.1.1. с=0, знаки одинаковы. Получим
уравнение плоскости
2.1.2. , знаки и с одинаковы:
- нет решений:
Слайд 272. Одно из собственных чисел равно нулю (
2.1.3. , знаки одинаковы и отличаются от знака с:
- эллиптический цилиндр
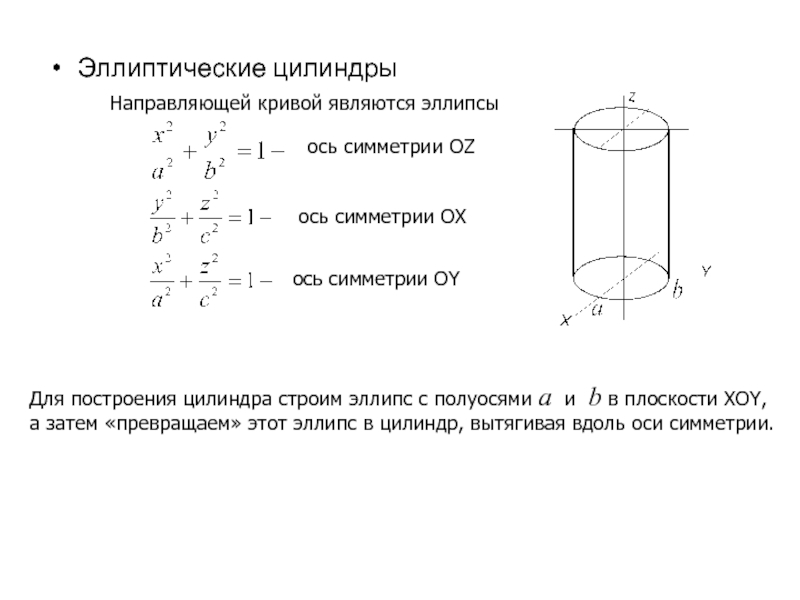
Слайд 28Эллиптические цилиндры
ось симметрии OZ
ось симметрии OX
ось симметрии OY
Для построения цилиндра
а затем «превращаем» этот эллипс в цилиндр, вытягивая вдоль оси симметрии.
Направляющей кривой являются эллипсы
Слайд 292. Одно из собственных чисел равно нулю (
2.1.4. с=0, знаки различны. Получим
уравнение плоскостей
2.1.5. , знаки различны:
- получим гиперболический цилиндр:
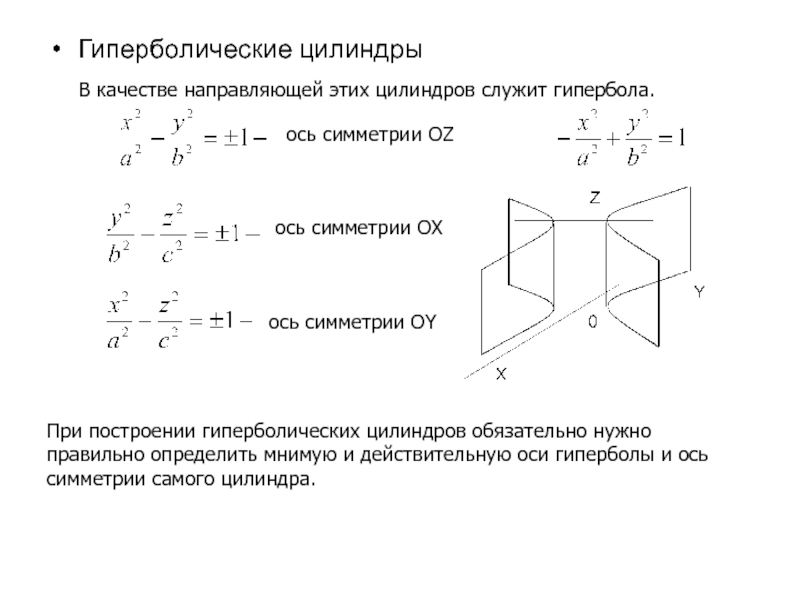
Слайд 30Гиперболические цилиндры
ось симметрии OZ
ось симметрии OX
ось симметрии OY
При построении гиперболических цилиндров
правильно определить мнимую и действительную оси гиперболы и ось
симметрии самого цилиндра.
В качестве направляющей этих цилиндров служит гипербола.
Слайд 312. Одно из собственных чисел равно нулю (
2.2.
Выделим полные квадраты
выполним параллельный перенос
получим
Слайд 322. Одно из собственных чисел равно нулю (
Преобразуем
Получим каноническое уравнение параболоида
Слайд 33Параболоиды
Канонические уравнения параболоидов можно записать
в общем виде
Таким образом, в уравнении отсутствует
В зависимости от знака между квадратами двух других переменных различают эллиптические и гиперболические параболоиды
Признаки уравнения эллиптического или кругового параболоида:
Отсутствие квадрата одной из переменных
Одинаковые знаки при квадратах переменных в левой части уравнения
Эллиптический
параболоид
Слайд 34Гиперболический параболоид
Каноническое уравнение гиперболического параболоида имеет вид
Признаки уравнения гиперболического параболоида:
Отсутствие
Разные знаки при квадратах переменных в левой
части уравнения
Отличительным признаком уравнения гиперболического параболоида
является то что в левой части уравнения между квадратами
переменных знак минус.
Эта поверхность имеет форму седла.
Слайд 353. Два собственных числа равны нулю (
Выделим полный квадрат
выполним параллельный перенос
Получим
Слайд 363. Два собственных числа равны нулю (
3.1. , получим
Это есть либо уравнения пересекающихся плоскостей, либо уравнение плоскости или нет решения.
Слайд 373. Два собственных числа равны нулю (
3.2. хотя бы один из :
перенос:
поворот:
Подбираем угол таким образом, чтобы пропал коэффициент при z: - параболический цилиндр
Слайд 38Параболические цилиндры
ось симметрии OZ
ось симметрии OZ
ось симметрии OX
ось симметрии
ось симметрии OY
ось симметрии OY
При построении цилиндра нужно определить основные параметры параболы:
координаты вершины, ось симметрии и направление ветвей, построить
параболу, а затем уже строить цилиндр с соответствующей осью симметрии.
Направляющей этих цилиндров является парабола.