- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ по математике 2012. (Часть 2) презентация
Содержание
- 1. ЕГЭ по математике 2012. (Часть 2)
- 2. Дано уравнение а) Решите уравнение б)
- 3. Изобразим промежуток
- 4. а) Решите уравнение
- 5. Значит на данном отрезке единственный корень
- 6. Это уравнение равносильно совокупности:
- 7. Сложный дискриминант и отбор корней. Решите
- 8. Выполним обратную замену: Для того, чтобы ответить
- 9. С2. Основанием прямой призмы ABCA1B1C1 является равнобедренный
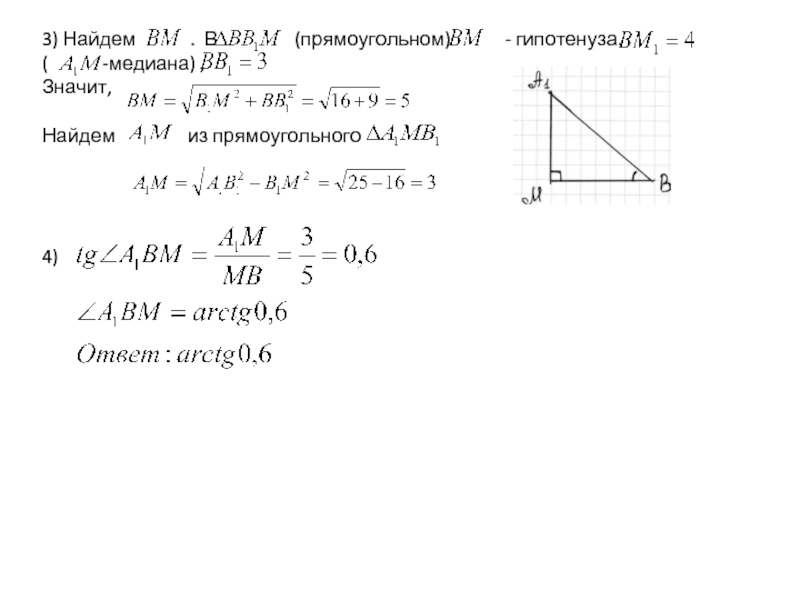
- 10. 3) Найдем
- 11. С2. В правильной четырехугольной призме
- 12. 4) В
Слайд 2Дано уравнение
а) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку
Решение:
а) Используем
(IV четверть, название меняется)
Новое уравнение:
Данное уравнение равносильно совокупности:
Значит, ответ на первый вопрос:
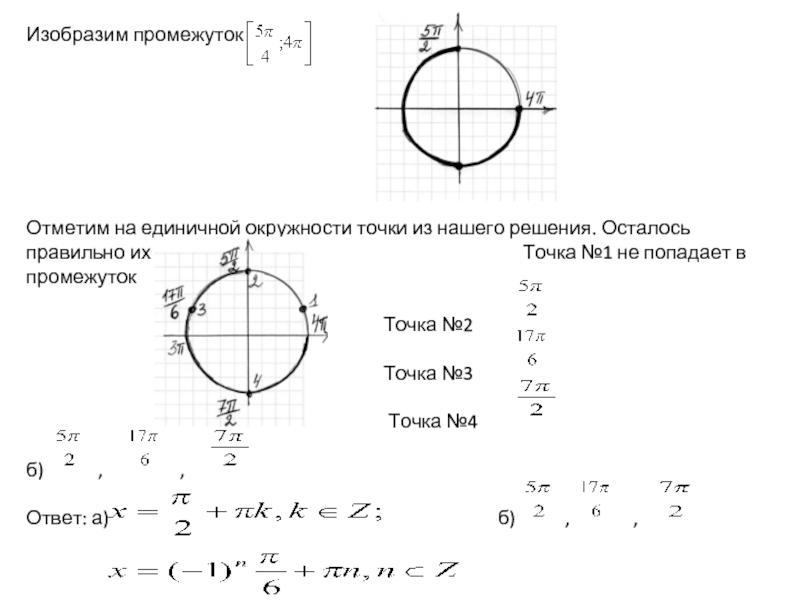
Слайд 3Изобразим промежуток
Отметим на единичной окружности точки из нашего решения. Осталось правильно
Точка №2
Точка №3
Точка №4
б) , ,
Ответ: а) б) , ,
Слайд 4а) Решите уравнение
б) Укажите корни этого уравнения,
Решение: а) преобразуем уравнение:
-однородное уравнение первой степени
б) Составим неравенство
Слайд 5Значит на данном отрезке единственный корень
Ответ: а)
3) а) Решите уравнение
б) Укажите корни, принадлежащие промежутку
Решение: Преобразуем левую часть уравнения:
Коэффициент указывает на возможность группировки:
Слайд 6Это уравнение равносильно совокупности:
однород-
ное уравнение II степени.
-это ответ на первый вопрос
б)
Ответ: а)
б)
Слайд 7Сложный дискриминант и отбор корней.
Решите уравнение:
и найдите все его корни
Решение: а) преобразуем левую часть уравнения:
Слайд 8Выполним обратную замену:
Для того, чтобы ответить на второй вопрос, надо знать
б)
Слайд 9С2. Основанием прямой призмы ABCA1B1C1 является равнобедренный треугольник ABC, AB=AC=5, BC=8.
Решение: Нужно найти угол между прямой и плоскостью, а значит, угол между прямой и ее проекцией на эту плоскость.
Опустим перпендикуляр А1М на плоскость ВСС1.
(так как призма прямая), а значит
Тогда прямая BM будет проекцией A1B на плоскость BCC1
2)Теперь мы знаем, что искомый угол равен углу A1BM.
Сделаем вынесенный чертеж.
прямоугольный (
а значит для поиска надо найти две любые
стороны.
Слайд 11С2. В правильной четырехугольной призме
до плоскости .
Решение: 1) Удобно ввести в рассмотрение треугольную пирамиду .
Ее высота из вершины на плоскость и даст
нам искомое расстояние.
2) Рассмотрим объем этой пирамиды двумя способами:
а)
б) «Перевернем» пирамиду, взяв в качестве вершины
3) Эти два объема , естественно, равны, значит
-искомое расстояние. Остается найти