- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности второго порядка презентация
Содержание
- 1. Поверхности второго порядка
- 2. Формирование линий 2-го порядка Все поверхности 2-го
- 3. Линии 2-го порядка Линии 2-го порядка
- 4. Условия на коэффициенты Эти три вида кривых
- 5. Матричное представление
- 6. Канонический вид В каноническом представлении имеются только
- 7. Приведение к каноническому виду
- 8. Приведение к каноническому виду
- 9. Эллипс Эллипсом называется множество точек плоскости, сумма
- 10. Эллипс
- 11. Гипербола Гиперболой называется множество точек плоскости, абсолютная
- 12. Гипербола
- 13. Парабола Параболой называется множество точек плоскости, равноудаленных
- 14. Парабола
- 15. Поверхность 1-го порядка
- 16. Матричное представление
- 17. Поверхность 2-го порядка
- 18. Матричное представление
- 19. Вектор нормали
- 20. Эллипсоид
- 21. Однополостный гиперболоид
- 22. Двуполостный гиперболоид
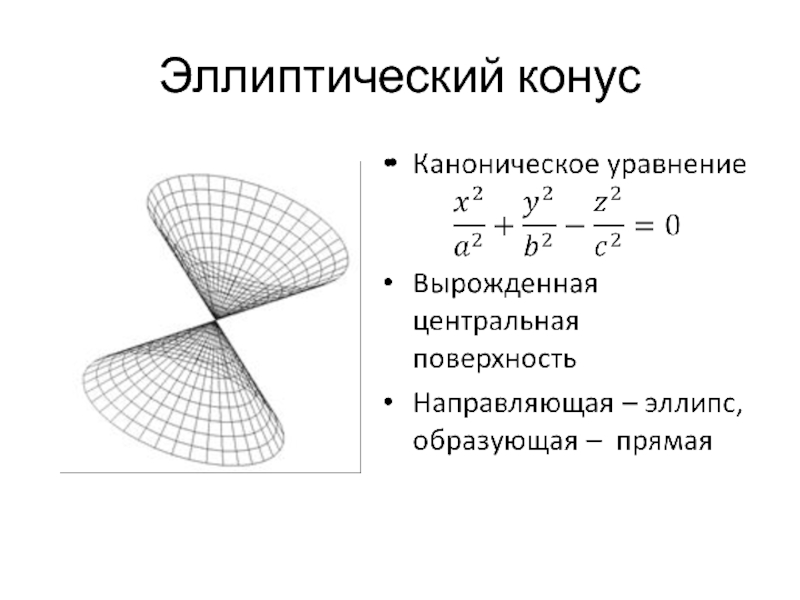
- 23. Эллиптический конус
- 24. Гиперболический параболоид
- 25. Эллиптический параболоид
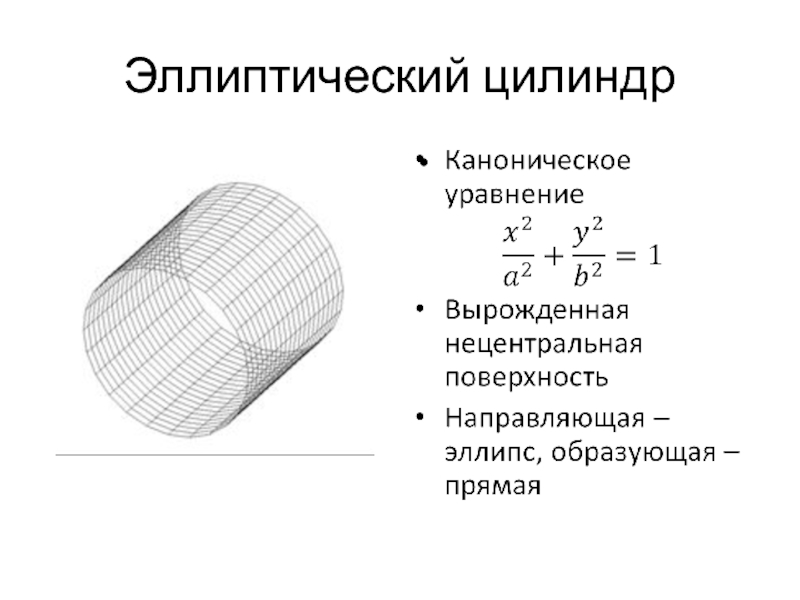
- 26. Эллиптический цилиндр
- 27. Параболический цилиндр
- 28. Гиперболический цилиндр
Слайд 2Формирование линий 2-го порядка
Все поверхности 2-го порядка получаются перемещением линий 1-го
или 2-го порядка – образующих, вдоль линий 1-го или 2-го порядка – направляющих
Слайд 3Линии 2-го порядка
Линии 2-го порядка являются плоскими линиями, т.е. любые
три их точки принадлежат одной плоскости
В плоскости Z = 0, уравнение кривой 2-го порядка имеет вид:
A*x2 + B*y2 + 2*C*x*y + 2*D*x + 2*E*y + F = 0
К кривым второго порядка относятся: эллипс, гипербола, парабола
В плоскости Z = 0, уравнение кривой 2-го порядка имеет вид:
A*x2 + B*y2 + 2*C*x*y + 2*D*x + 2*E*y + F = 0
К кривым второго порядка относятся: эллипс, гипербола, парабола
Слайд 4Условия на коэффициенты
Эти три вида кривых различаются условиями, которым удовлетворяют коэффициенты
A и C
если A*C > 0, то эллипс (окружность)
если A*C < 0, то гипербола
если A*C = 0, то парабола
если A*C > 0, то эллипс (окружность)
если A*C < 0, то гипербола
если A*C = 0, то парабола
Слайд 6Канонический вид
В каноническом представлении имеются только члены с квадратами переменных и
свободный член
Приведение уравнения к каноническому виду осуществляется линейной заменой переменных, которая представляет собой комбинацию преобразований поворота и смещения
Приведение уравнения к каноническому виду осуществляется линейной заменой переменных, которая представляет собой комбинацию преобразований поворота и смещения
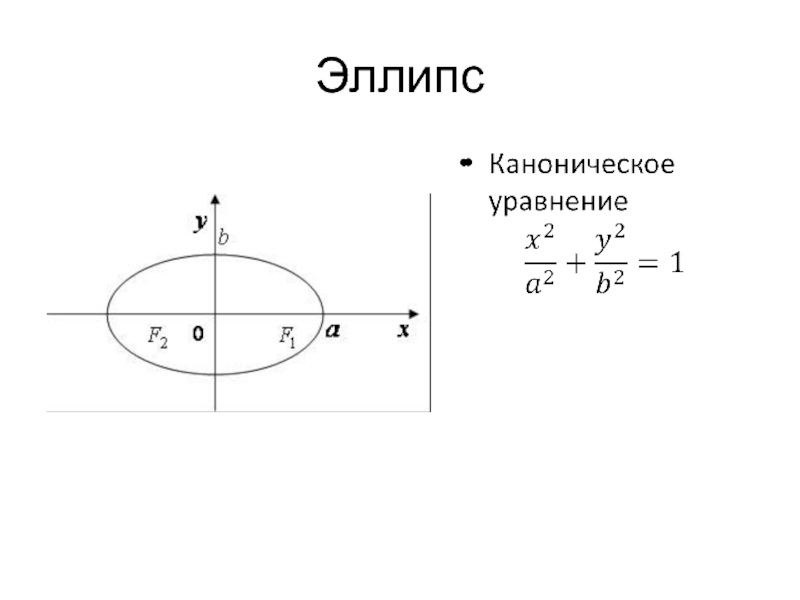
Слайд 9Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных
точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами)
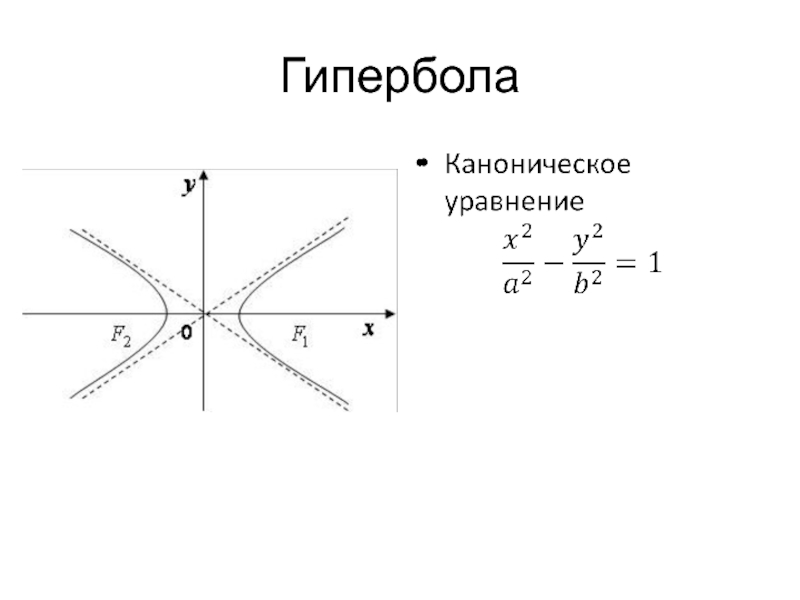
Слайд 11Гипербола
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до
двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами
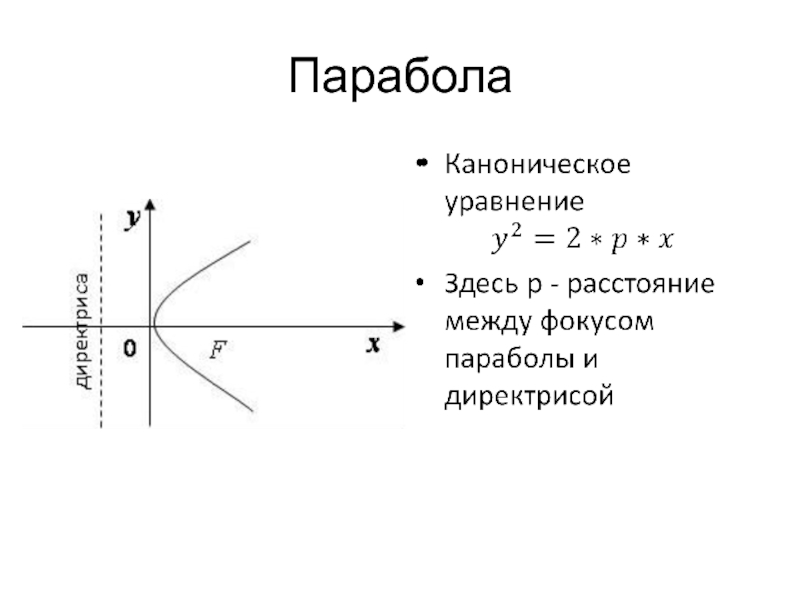
Слайд 13Парабола
Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и
прямой, называемой директрисой