- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия теории множеств презентация
Содержание
- 1. Основные понятия теории множеств
- 2. 1.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МНОЖЕСТВ 1.1.1. Множества, способы задания множеств
- 3. Определение Кантора. Под множеством понимают
- 4. Множество — это совокупность объектов
- 5. Объекты, образующие множество, называются элементами множества
- 6. Если множество конечно, то число
- 7. Множество A является подмножеством множества B,
- 8. Равенство множеств. Множества A и B равны
- 9. Если ,
- 10. Диаграмма Венна (также используется название диаграмма Эйлера
- 11. Пример. Диаграмма
- 12. Пример кругов
- 13. Одним из частных случаев является ситуация, когда
- 14. Если в рамках некоторого класса задач
- 15. Способы задания множеств: 1. Перечислением всех
- 16. 3. Описанием характеристик и свойств, которыми обладают все элементы множества. Например,
- 17. 1.2.1. Основные операции над множествами и их свойства
- 18. Основные операции над множествами: объединение множеств; пересечение множеств; разность множеств; симметричная разность; дополнение.
- 19. 1. Объединение множеств
- 20. 2. Пересечение множеств
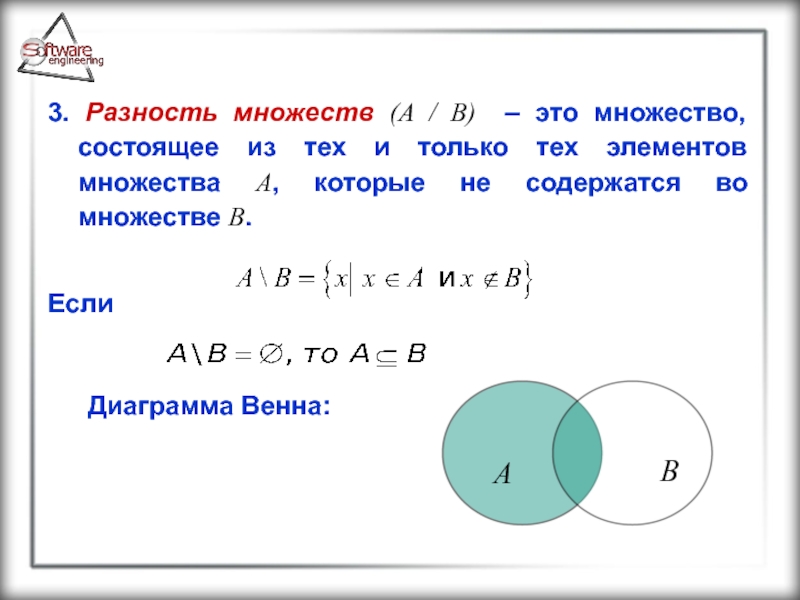
- 21. 3. Разность множеств (A / B) –
- 22. 4. Симметричная разность
- 23. 5. Дополнением множества A до множества U
- 24. Основные свойства операций над множествами. Для всех
- 29. 1.2 ПРЯМОЕ ПРОИЗВЕДЕНИЕ МНОЖЕСТВ
- 30. Вектором (кортежем) называется упорядоченный набор элементов.
- 31. Прямым или декартовым произведением множеств
- 32. Пример.
- 33. Пусть имеется множество A, элементы которого являются
- 34. Проекцией вектора
1.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МНОЖЕСТВ 1.1.1. Множества, способы задания множеств
Слайд 3
Определение Кантора. Под множеством понимают объединение в одно целое объектов,
хорошо различимых нашей интуицией или нашей мыслью.
Гео́рг Ка́нтор (нем. Georg Ferdinand Ludwig Philipp Cantor, 3 марта 1845, Санкт-Петербург — 6 января 1918, Галле (Заале)) — немецкий математик. Он наиболее известен как создатель теории множеств, ставшей краеугольным камнем в математике.
Слайд 4
Множество — это совокупность объектов любой природы, рассматриваемая как единое целое.
Обычно
множества обозначают прописными латинскими буквами .
Пример. Множество натуральных чисел
Пример. Множество натуральных чисел
Слайд 5
Объекты, образующие множество, называются элементами множества (обозначаются маленькими буквами). Если элемент
a входит во множество A, то это обозначается так:
Запись вида
означает, что элемент не принадлежит множеству .
Множество, содержащее конечное число элементов, называется конечным (в противном случае – бесконечным).
Запись вида
означает, что элемент не принадлежит множеству .
Множество, содержащее конечное число элементов, называется конечным (в противном случае – бесконечным).
Слайд 6
Если множество конечно, то число его элементов называется мощностью множества и
обозначается.
Если множество не содержит ни одного элемента, то оно называется пустым.
Если множество не содержит ни одного элемента, то оно называется пустым.
∅
Слайд 7
Множество A является подмножеством множества B, если любой элемент A принадлежит
также множеству B.
Слайд 8Равенство множеств.
Множества A и B равны тогда и только тогда, когда
их элементы совпадают. В этом случае пишут:
Так как при равенстве множеств A и B во множестве A нет элементов, не принадлежащих B, а в B нет элементов не принадлежащих A, то признаком равенства множеств является одновременное выполнение двух условий:
Так как при равенстве множеств A и B во множестве A нет элементов, не принадлежащих B, а в B нет элементов не принадлежащих A, то признаком равенства множеств является одновременное выполнение двух условий:
Слайд 10 Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное
изображение всех возможных пересечений нескольких (часто — трёх) множеств.
Эйлер, Леонард (1707—1783) — швейцарский, немецкий и российский математик и механик.
Джон Венн английский логик и философ. Он известен тем, что ввёл диаграммы Эйлера — Венна, которые используются во многих областях, таких как теория множеств, теория вероятностей, логика, статистика и информатика.
Слайд 11
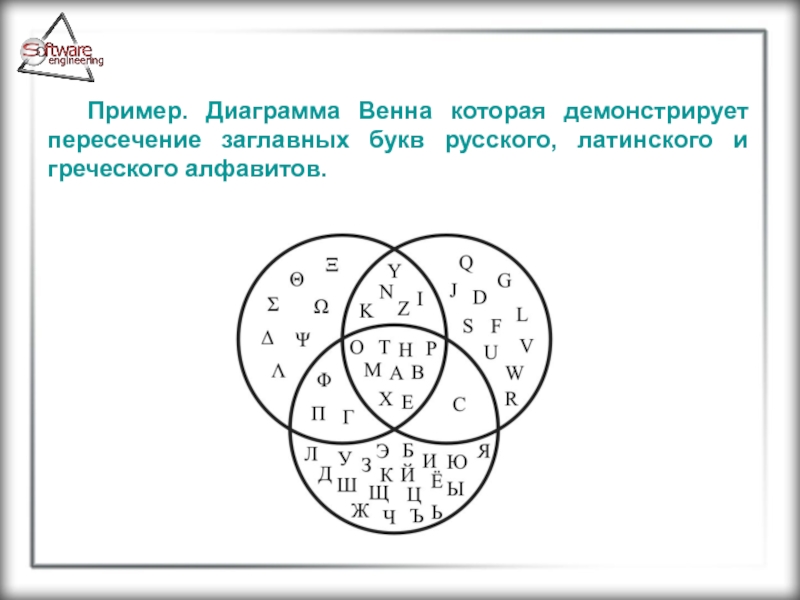
Пример. Диаграмма Венна которая демонстрирует пересечение заглавных букв русского, латинского и
греческого алфавитов.
Слайд 12
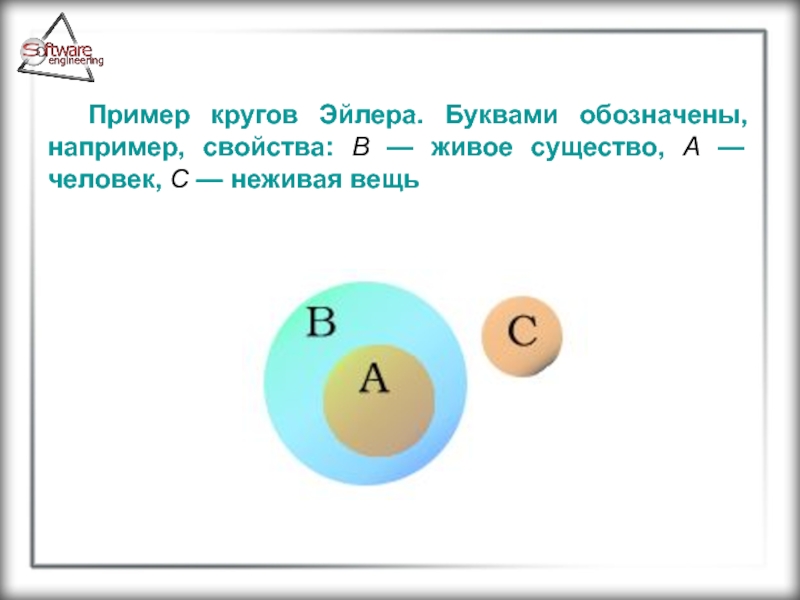
Пример кругов Эйлера. Буквами обозначены, например, свойства: B — живое существо,
A — человек, C — неживая вещь
Слайд 13 Одним из частных случаев является ситуация, когда элементами некоторого множества являются
другие множества.
Пример 1. Пусть – множество футболистов команды «Спартак», – множество команд высшей лиги.
Пример 2. Пусть A={1,3,5,7}, D={2,4,6,8}.
B={A,B}={{1,3,5,7},{2,4,6,8}}
Вопрос. 1. Равны ли множества Ø и {Ø}?
2.Является ли множеством следующая совокупность элементов {1,2,3,1,7,5}?
3. Равны ли множества A={1,2,3} и B={3,2,1}?
Пример 1. Пусть – множество футболистов команды «Спартак», – множество команд высшей лиги.
Пример 2. Пусть A={1,3,5,7}, D={2,4,6,8}.
B={A,B}={{1,3,5,7},{2,4,6,8}}
Вопрос. 1. Равны ли множества Ø и {Ø}?
2.Является ли множеством следующая совокупность элементов {1,2,3,1,7,5}?
3. Равны ли множества A={1,2,3} и B={3,2,1}?
Слайд 14
Если в рамках некоторого класса задач рассматриваются различные множества, то полная
совокупность всех элементов, из которых могут формироваться все множества и подмножества, образует универсальное множество – “Универсум” или полное пространство.
Обозначается универсальное множество символом U (генеральная совокупность).
Обозначается универсальное множество символом U (генеральная совокупность).
Слайд 15Способы задания множеств:
1. Перечислением всех его элементов.
Пример. A={a,b,c,d} ;
B={0,1,3,8,9}
2. Порождающей процедурой. Порождающая процедура представляет собой правило получения элементов множества на основе уже имеющихся элементов либо из других объектов. Элементами множества считаются все объекты, которые получены с помощью этой процедуры.
Пример. В={b | b=π/2±kπ, k - принадлежит множеству натуральных чисел} или C={x | H(x)}
2. Порождающей процедурой. Порождающая процедура представляет собой правило получения элементов множества на основе уже имеющихся элементов либо из других объектов. Элементами множества считаются все объекты, которые получены с помощью этой процедуры.
Пример. В={b | b=π/2±kπ, k - принадлежит множеству натуральных чисел} или C={x | H(x)}
Слайд 18
Основные операции над множествами:
объединение множеств;
пересечение множеств;
разность множеств;
симметричная разность;
дополнение.
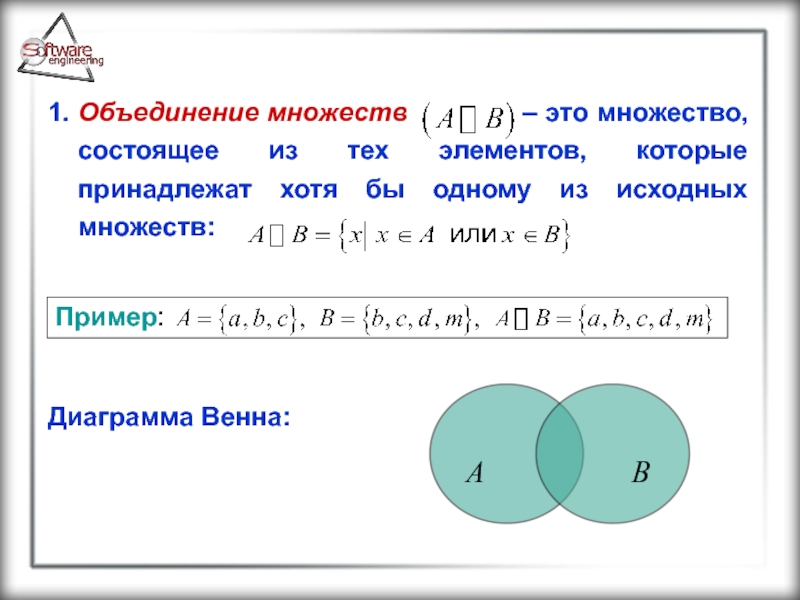
Слайд 191. Объединение множеств – это
множество, состоящее из тех элементов, которые принадлежат хотя бы одному из исходных множеств:
Диаграмма Венна:
Диаграмма Венна:
Пример:
A
B
Слайд 202. Пересечение множеств – это
множество тех и только тех элементов, которые принадлежат и множеству A, и множеству B:
Диаграмма Венна:
Диаграмма Венна:
Пример:
A
B
Слайд 213. Разность множеств (A / B) – это множество, состоящее из
тех и только тех элементов множества A, которые не содержатся во множестве B.
Если
Диаграмма Венна:
Если
Диаграмма Венна:
A
B
Слайд 224. Симметричная разность – это
множество элементов, принадлежащих множествам A или B за исключением их общих элементов
Диаграмма Венна:
Диаграмма Венна:
A
B
Слайд 23 5. Дополнением множества A до множества U (обозначается ) называется множество
всех элементов U, не принадлежащих множеству A.
Пример. Если A – это множество студентов кафедры ПОВТ, U – множество всех студентов ЮРГПУ (НПИ), то дополнением A будет множество всех студентов университета, кроме студентов кафедры ПОВТ
Диаграмма Венна:
Пример. Если A – это множество студентов кафедры ПОВТ, U – множество всех студентов ЮРГПУ (НПИ), то дополнением A будет множество всех студентов университета, кроме студентов кафедры ПОВТ
Диаграмма Венна:
U
A
Слайд 24 Основные свойства операций над множествами. Для всех множеств A,B,С и универсального
множества U справедливы следующие равенства:
Слайд 30
Вектором (кортежем) называется упорядоченный набор элементов. Элементы, образующие вектор, называются координатами
или компонентами. Координаты нумеруются слева направо. Число координат называется длиной или размерностью вектора.
В отличие от элементов множества координаты вектора могут совпадать. Обозначение вектора: (a,b,c), где a,b,c – координаты вектора.
Два вектора равны, если они имеют одинаковую длину и равны их соответствующие координаты.
В отличие от элементов множества координаты вектора могут совпадать. Обозначение вектора: (a,b,c), где a,b,c – координаты вектора.
Два вектора равны, если они имеют одинаковую длину и равны их соответствующие координаты.
Слайд 31
Прямым или декартовым произведением множеств A и B (обозначается
), называется множество всех упорядоченных пар (a,b) таких, что
Слайд 33 Пусть имеется множество A, элементы которого являются символами (буквы, цифры, знаки).
Такое множество называется алфавитом. Элементы множества – слова.
Множество – это множество точек (пар координат) плоскости (здесь R – множество всех действительных чисел). Декартово произведение.
Теорема 1.1. Пусть – конечные множества и их мощности известны:
Тогда
Частный случай: .
Множество – это множество точек (пар координат) плоскости (здесь R – множество всех действительных чисел). Декартово произведение.
Теорема 1.1. Пусть – конечные множества и их мощности известны:
Тогда
Частный случай: .
Слайд 34
Проекцией вектора
на ось i (обозначается ) называется его компонента ai. Проекцией вектора на оси
называется вектор длины k.
Если – множество векторов одинаковой длины, то проекцией на i-ю ось называется множество проекций всех на эту ось:
называется вектор длины k.
Если – множество векторов одинаковой длины, то проекцией на i-ю ось называется множество проекций всех на эту ось:
