- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие обратной функции презентация
Содержание
- 1. Понятие обратной функции
- 2. Если функция у = f
- 3. Пусть у = f(x) – обратимая функция.
- 4. Не для всякой функции можно указать обратную.
- 5. ПРИВЕДЕМ ПРИМЕР.
- 6. y=11-5x x= (11-y)/5 y = (11-x)/5 Графики взаимно-обратных функций симметричны относительно прямой y=x. ПРИМЕР 2.
- 7. Дана функция: Найдем обратную ей функцию.
- 8. х х у
- 9. Свойства обратных функций 1. Область определения обратной
Слайд 1
Обратная функция — функция, обращающая зависимость, выражаемую данной функцией.
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ.
Слайд 2
Если функция у = f ( х ) принимает каждое своё
значение у только при одном значении х, то эту функцию называют обратимой.
Слайд 3Пусть у = f(x) – обратимая функция. Тогда каждому у из
множества значений функции соответствует одно определённое число х из области её определения, такое, что f(x) = y. Это соответствие определяет функцию х от у, которую обозначим х = g(y). Поменяем местами х и у: у = g(x).
Функцию у = g(x) называют обратной к функции у = f(x)
Функцию у = g(x) называют обратной к функции у = f(x)
Слайд 4Не для всякой функции можно указать обратную. Условие обратимости функции -
ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.
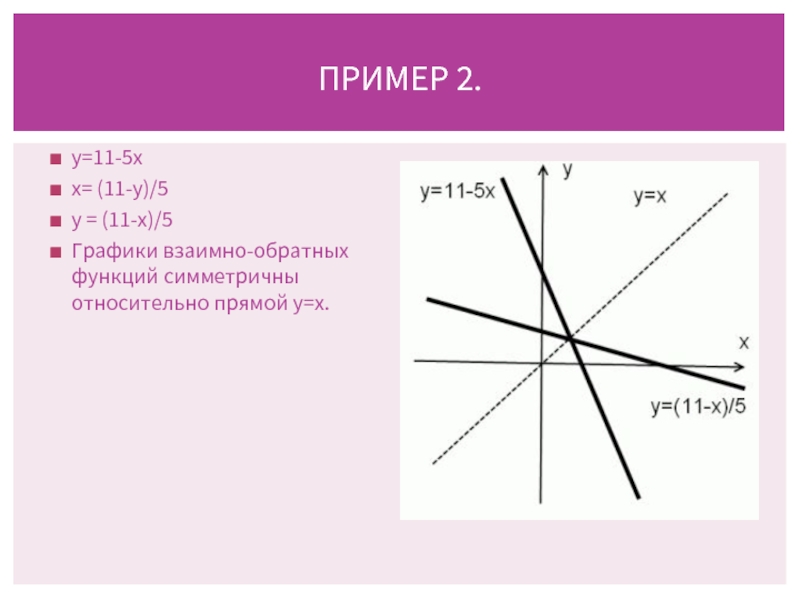
Слайд 6y=11-5x
x= (11-y)/5
y = (11-x)/5
Графики взаимно-обратных функций симметричны относительно прямой y=x.
ПРИМЕР 2.
Слайд 9Свойства обратных функций
1. Область определения обратной функции f(-х) совпадает с множеством
значений исходной f(х), а множество значений обратной функции f(-х)с овпадает с областью определения исходной функции f(х):
D(f(-x)) = E(f(x)), E(f(-x)) = D(f(-x)).
2. Монотонная функция является обратимой:
если функция f(x) возрастает, то обратная к ней функция f(-x) также возрастает;
если функция f(x) убывает, то обратная к ней функция f(-x) также убывает.
D(f(-x)) = E(f(x)), E(f(-x)) = D(f(-x)).
2. Монотонная функция является обратимой:
если функция f(x) возрастает, то обратная к ней функция f(-x) также возрастает;
если функция f(x) убывает, то обратная к ней функция f(-x) также убывает.