- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Додавання раціональних чисел презентация
Содержание
- 1. Додавання раціональних чисел
- 2. МЕТА: сформувати уявлення про зміст дії додавання
- 3. "Краще вчиться не той, хто
- 4. «Хто володіє інформацією, той володіє
- 5. Не складно перевірити… Порівняйте числа
- 6. Не складно перевірити… 2. Порівняти модулі
- 7. Не складно перевірити… 3. Обчислити :
- 8. Як знайти суму додатного і від’ємного числа?
- 9. Виникли від'ємні числа в Китаї в
- 10. З історії від'ємних чисел
- 11. Виконайте додавання за допомогою координатної прямої
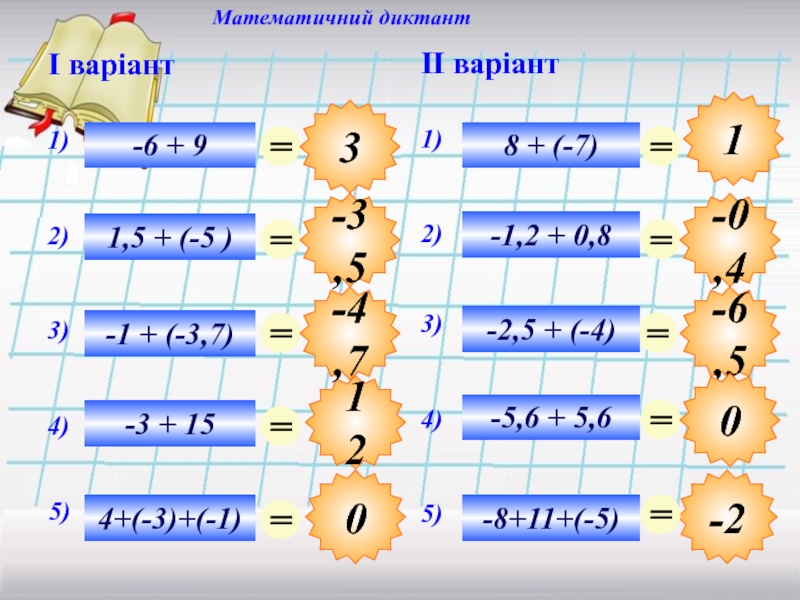
- 12. 12 Математичний диктант I варіант II варіант
- 13. ДИВИСЬ НА ЗНАКИ ЧИСЕЛ ОДНАКОВІ РІЗНІ
- 14. ЧИ ПРАВИЛЬНО ВИКОНАНО ДОДАВАННЯ? -15 + 10
- 15. ЧИ ПРАВИЛЬНО ВИКОНАНО ДОДАВАННЯ? - 6 +
- 16. ЧИ ПРАВИЛЬНО ВИКОНАНО ДОДАВАННЯ? - 6
- 17. Колективне розв`зування вправ:
- 18. Математичне лото
- 19. “Сума майна і майна є майно”
- 20. Домашнє завдання Прочитати § 26, вивчити правила Виконати № 1125, 1128, 1144
МЕТА: сформувати уявлення про зміст дії додавання раціональних чисел; вивести правила додавання від'ємних чисел та чисел з різними знаками і виробити вміння застосовувати ці правила для розв'язування задач
Слайд 2МЕТА:
сформувати уявлення про зміст дії додавання раціональних чисел;
вивести правила додавання
від'ємних чисел та чисел з різними знаками і виробити вміння застосовувати ці правила для розв'язування задач
Слайд 3 "Краще вчиться не той, хто старанно запам'ятовує прочитане, а
той, хто набуває вміння використати його".
Слайд 4
«Хто володіє інформацією, той володіє світом»
. Що таке координатна пряма?
Де на координатній прямій розміщені точки, які відповідають додатним числам; від’ємним числам?
Які числа називають протилежними? Наведіть приклади.
Що таке модуль числа?
Чому дорівнює модуль додатного числа?
Чому дорівнює модуль від’ємного числа?
Чи існують числа, модуль яких дорівнює нулю?
Як можна порівняти числа за допомогою координатної прямої?
Яке число більше: додатне чи від’ємне?
Яке із двох від’ємних чисел більше?
Які числа називають протилежними? Наведіть приклади.
Що таке модуль числа?
Чому дорівнює модуль додатного числа?
Чому дорівнює модуль від’ємного числа?
Чи існують числа, модуль яких дорівнює нулю?
Як можна порівняти числа за допомогою координатної прямої?
Яке число більше: додатне чи від’ємне?
Яке із двох від’ємних чисел більше?
Слайд 7Не складно перевірити…
3. Обчислити :
│ -2,3 │ + │ 4 │
= 6,3;
│ 6,12 │ - │ -5,9 │ = 0,22;
│ 5,23 │ + │ -4,3 │ = 9,53;
│ -9, 56 │ - │ 0 │ =9,56;
│ 6,12 │ - │ -5,9 │ = 0,22;
│ 5,23 │ + │ -4,3 │ = 9,53;
│ -9, 56 │ - │ 0 │ =9,56;
Слайд 8Як знайти суму додатного і від’ємного числа? - 4 + 7 =
?
3 + (- 4)=?
Як додати два від’ємних
числа?
-2 + (-3 ) = ?
Слайд 9
Виникли від'ємні числа в Китаї в ІІ ст. до н.е. у
зв'язку з розв'язуванням рівнянь
Додатні числа позначали “майно”, “прибуток”.
Ім раділи і позначали червоним кольором.
Китайці їх називали «чен».
Від‘ємні числа означали “борг”, “збиток”.
Зображали чорним кольором і називали «фу».
Додатні числа позначали “майно”, “прибуток”.
Ім раділи і позначали червоним кольором.
Китайці їх називали «чен».
Від‘ємні числа означали “борг”, “збиток”.
Зображали чорним кольором і називали «фу».
З історії від'ємних чисел
Слайд 10
З історії від'ємних чисел
Індійські математики уявляли собі додатні числа як «майно»,
а від’ємні як “борг”.
Ось як індійський математик Брахмагупа (VII ст.) трактував правила додавання і віднімання:
“Сума двох боргів є борг”
“Сума майна і майна є майно”
“Сума майна та боргу дорівнює їх різниці”
“Сума майна і такого самого боргу дорівнює нулю”
Ось як індійський математик Брахмагупа (VII ст.) трактував правила додавання і віднімання:
“Сума двох боргів є борг”
“Сума майна і майна є майно”
“Сума майна та боргу дорівнює їх різниці”
“Сума майна і такого самого боргу дорівнює нулю”
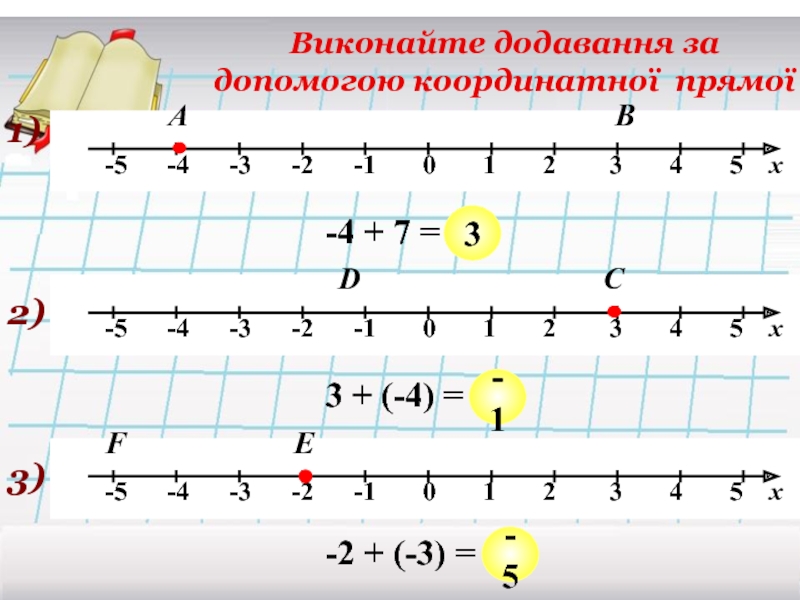
Слайд 11Виконайте додавання за допомогою координатної прямої
1)
А
-4 + 7 = …
В
2)
С
D
3 +
(-4) = …
3)
Е
F
-2 + (-3) = …
3
-1
-5
Слайд 13ДИВИСЬ НА ЗНАКИ ЧИСЕЛ
ОДНАКОВІ
РІЗНІ
СТАВ СПІЛЬНИЙ ЗНАК
Став знак числа, що має
більший модуль
Модулі
відняти
МОДУЛІ ДОДАТИ
АЛГОРИТМ ДОДАВАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ
Слайд 14ЧИ ПРАВИЛЬНО ВИКОНАНО ДОДАВАННЯ?
-15 + 10 = │-15│ – │10│ =
15- – 10 = 5
-15 + 10 = -(│-15│ – │10│) =
= -(15 – 10) = - 5
-15 + 10 = -(│-15│ – │10│) =
= -(15 – 10) = - 5
Слайд 15ЧИ ПРАВИЛЬНО ВИКОНАНО ДОДАВАННЯ?
- 6 + (- 5) = - (
│- 6│- │- 5│) =
= - ( 6 - 5 ) = - 1
= - ( 6 - 5 ) = - 1
- 6 + (- 5) = - ( │- 6│+ │- 5│) = = - ( 6 + 5 ) = - 11
Слайд 16ЧИ ПРАВИЛЬНО ВИКОНАНО ДОДАВАННЯ?
- 6 + 20 = - (│
20│ - │-6 │) =
= - ( 20 – 6 ) = -14
= - ( 20 – 6 ) = -14
- 6 + 20 = + (│ 20│ - │-6 │) =
= 20 – 6 = 14
Слайд 19
“Сума майна і майна є майно”
“Сума двох боргів є борг”
“Сума майна
та боргу дорівнює їх різниці”
“Сума майна і такого самого боргу дорівнює нулю”
“Сума майна і такого самого боргу дорівнює нулю”
Сума двох додатних чисел є числом додатним
Сума двох від’ємних чисел є числом від'ємним
Сума двох чисел із різними знаками дорівнює різниці їх модулів і має знак більшого за модулем доданка
Сума протилежних чисел дорівнює нулю
