Преподаватель: Лихачева Е.С.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие множества. Способы задания множеств. Операции над множествами презентация
Содержание
- 1. Понятие множества. Способы задания множеств. Операции над множествами
- 2. Понятие множества и элементы множества Множество – определенная
- 3. Для перечисленных множеств чисел справедливо следующее высказывание:
- 4. Характеристическое свойство элементов множества Если множество состоит
- 5. Способы задания множеств Если множество состоит из
- 6. Способы задания множеств 1) Перечислением всех элементов множества в
- 7. Отношения между множествами Пусть во множестве A задано некоторое
- 8. Пересечение множеств Пересечением множеств A и B называется множество, в которое входят
- 9. Объединение множеств Объединением двух множеств A и B называется множество, состоящее из
- 10. Свойства пересечения и объединения множеств Пересечение и
- 11. Вычитание множеств Разностью двух множеств A и B называется такое множество, в
- 12. Декартово произведение множеств Прямое или декартово произведение двух множеств — это множество, элементами которого
- 13. Пример 1. Найдите объединение и пересечение множеств А и В,
- 14. Решение задач Пример 2. В гимназии все
- 15. Решение задач Пример 3. Баба Яга в своей
- 16. Решение задач Решение. Из условия задачи следует, что
- 17. Решение задач Пример 4. В первом пенале лежат
- 18. Решение задач Решение: В четвёртом пенале должны лежать
- 19. Самостоятельная работа: Написать конспекты по темам: Понятие
Слайд 1Учебный модуль 1
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Тема 1.2.
Понятие множества. Способы задания множеств.
Операции над множествами
Слайд 2Понятие множества и элементы множества
Множество – определенная совокупность объектов.
Объекты, из которых состоит
множество, называются элементами множества.
ПРИМЕР: Множество домов на данной улице, множество натуральных чисел, множество студентов группы и т. д.
Множества обычно обозначают заглавными латинскими буквами А, В, С, D, X, Y…, элементы множества строчными латинскими буквами – a, b, c, d, x, y…
Для обозначения того, что объект x является элементом множества A, используют символику: x∈А (читается: x принадлежит А ), запись x∉А обозначает, что объект x не является элементом множества A (читается: x не принадлежит А).
Множество не содержащее ни одного элемента называется пустым (обозначается: Ø).
Множества из элементов которого составляем конкретное множество называется универсальным (обозначается: U).
ПРИМЕР: U – множество людей на земле, А – студенты вашей группы.
Множества можно изображать с помощью кругов, которые называются кругами Эйлера или диаграммами Венна, универсальное множество принято обозначать прямоугольником.
ПРИМЕР
ПРИМЕР: Множество домов на данной улице, множество натуральных чисел, множество студентов группы и т. д.
Множества обычно обозначают заглавными латинскими буквами А, В, С, D, X, Y…, элементы множества строчными латинскими буквами – a, b, c, d, x, y…
Для обозначения того, что объект x является элементом множества A, используют символику: x∈А (читается: x принадлежит А ), запись x∉А обозначает, что объект x не является элементом множества A (читается: x не принадлежит А).
Множество не содержащее ни одного элемента называется пустым (обозначается: Ø).
Множества из элементов которого составляем конкретное множество называется универсальным (обозначается: U).
ПРИМЕР: U – множество людей на земле, А – студенты вашей группы.
Множества можно изображать с помощью кругов, которые называются кругами Эйлера или диаграммами Венна, универсальное множество принято обозначать прямоугольником.
ПРИМЕР
Слайд 3Для перечисленных множеств чисел справедливо следующее высказывание:
N ⊂ Z ⊂ Q
⊂ R
Множество натуральных чисел принадлежит множеству целых чисел, которое принадлежит множеству рациональных чисел, которое принадлежит множеству действительных чисел.
Множество натуральных чисел принадлежит множеству целых чисел, которое принадлежит множеству рациональных чисел, которое принадлежит множеству действительных чисел.
Натуральные числа
Целые числа
Рациональные числа
Действительные числа
Слайд 4Характеристическое свойство элементов множества
Если множество состоит из небольшого количества элементов, то
его удобно задавать перечислением всех элементов, если же элементов много или множество имеет бесконечное число элементов, то оно задается с помощью характеристического предиката (свойства).
Слайд 5Способы задания множеств
Если множество состоит из небольшого количества элементов, то его
удобно задавать перечислением всех элементов, если же элементов много или множество имеет бесконечное число элементов, то оно задается с помощью характеристического предиката.
Слайд 6Способы задания множеств
1) Перечислением всех элементов множества в фигурных скобках.
ПРИМЕР: A = {Оля, Маша,
Саша}
2) Характеристическим предикатом, который описывает свойство всех элементов, входящих в множество. Характеристический предикат записывается после двоеточия или символа « | ».
ПРИМЕР: Р(x) = x ∈ N ∧ x < 8 - характеристический предикат.
M = {x : Р(x)} или M = {x : x ∈ N ∧ x < 8 }.
Множество M можно задать и перечислением его элементов:
M = {1, 2, 3, 4, 5, 6, 7}
ПРИМЕР
В = {x | x - четное натуральное число} = {2, 4, 6, 8, …}
2) Характеристическим предикатом, который описывает свойство всех элементов, входящих в множество. Характеристический предикат записывается после двоеточия или символа « | ».
ПРИМЕР: Р(x) = x ∈ N ∧ x < 8 - характеристический предикат.
M = {x : Р(x)} или M = {x : x ∈ N ∧ x < 8 }.
Множество M можно задать и перечислением его элементов:
M = {1, 2, 3, 4, 5, 6, 7}
ПРИМЕР
В = {x | x - четное натуральное число} = {2, 4, 6, 8, …}
Слайд 7Отношения между множествами
Пусть во множестве A задано некоторое отношение "○".
Определение . Отношение "○" рефлексивно, если для любого элемента a из
множества A выполнено a○a (т.е. любой элемент связан отношением ○ с самим собой).
Например: отношение равенства на множестве отрезков рефлексивно, так как любой отрезок равен сам себе.
Определение . Отношение ○ симметрично, если из a○b следует b○a для любых элементов a и b множества A. Отношение равенства на множестве отрезков является симметричным, так как если [AB] = [CD], то и [CD] = [AB].
Определение . Отношение ○ называется транзитивным, если из того, что a○b и b○c следует, что a○c. В частности, отношение равенства отрезков рефлексивно, так как если отрезок AB равен отрезку CD, а отрезок CD равен отрезку MN, то отрезок AB равен отрезку MN.
Определение. Отношение ○ во множестве A называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.
Определение . Отношение ○ симметрично, если из a○b следует b○a для любых элементов a и b множества A. Отношение равенства на множестве отрезков является симметричным, так как если [AB] = [CD], то и [CD] = [AB].
Определение . Отношение ○ называется транзитивным, если из того, что a○b и b○c следует, что a○c. В частности, отношение равенства отрезков рефлексивно, так как если отрезок AB равен отрезку CD, а отрезок CD равен отрезку MN, то отрезок AB равен отрезку MN.
Определение. Отношение ○ во множестве A называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.
Слайд 8Пересечение множеств
Пересечением множеств A и B называется множество, в которое входят те и только те элементы,
которые одновременно принадлежат множествам A и B (общие элементы множеств A и B). Обозначение: A⋂B, где символ ⋂ – знак пересечения двух множеств. Два множества пересекаются, если A⋂B ≠∅ , и не пересекаются, если A⋂B =∅ .
Например: если две прямые a и b не пересекаются, то можно записать a ⋂ b = ∅, если же они пересекаются, то по определению их пересечением является общая точка A (a ⋂ b = A). Пересечением луча a с дополняющим его лучом a' является их общее начало O (a ⋂ a' = O).
Например: если две прямые a и b не пересекаются, то можно записать a ⋂ b = ∅, если же они пересекаются, то по определению их пересечением является общая точка A (a ⋂ b = A). Пересечением луча a с дополняющим его лучом a' является их общее начало O (a ⋂ a' = O).
Слайд 9Объединение множеств
Объединением двух множеств A и B называется множество, состоящее из тех элементов, которые принадлежат хотя
бы одному из этих множеств. Обозначение: A ∪ B, где символ ∪ – знак объединения множеств.
Например: объединением луча a с дополняющим его лучом a' является прямая.
Например: объединением луча a с дополняющим его лучом a' является прямая.
Слайд 10Свойства пересечения и объединения множеств
Пересечение и объединение множеств коммутативно (перестановочно):
A⋂B = B⋂A; A∪B = B∪A.
Пересечение и
объединение множеств ассоциативно: для любых множеств A, B и C имеем
(A⋂B)⋂C = A⋂(B⋂C); (A∪B)∪C = A∪(B∪C).
Если A⊂B, то A⋂B = A, A∪B=B.
Для любых множеств A, B и C справедливы равенства: а) A ⋂(B ∪ C) = (A ⋂ B) ∪(A ⋂ C), б) A ∪(B ⋂ C) = (A ∪ B) ⋂(A ∪ C)
(A⋂B)⋂C = A⋂(B⋂C); (A∪B)∪C = A∪(B∪C).
Если A⊂B, то A⋂B = A, A∪B=B.
Для любых множеств A, B и C справедливы равенства: а) A ⋂(B ∪ C) = (A ⋂ B) ∪(A ⋂ C), б) A ∪(B ⋂ C) = (A ∪ B) ⋂(A ∪ C)
Слайд 11Вычитание множеств
Разностью двух множеств A и B называется такое множество, в которое входят все те элементы,
которые принадлежат A и не принадлежат B. Обозначение: A \ B. Если B – подмножество A, то A \ B называют дополнением к B и обозначают B'.
Например: разностью прямой a и ее луча с началом O является множество точек дополняющего луча a' без начальной точки O.
Например: разностью прямой a и ее луча с началом O является множество точек дополняющего луча a' без начальной точки O.
Слайд 12Декартово произведение множеств
Прямое или декартово произведение двух множеств — это множество, элементами которого являются всевозможные упорядоченные пары элементов исходных множеств.
Пусть
даны два множества X и Y. Прямое произведение этих множеств есть такое множество X × Y, элементами которого являются упорядоченные пары (x,y) для всевозможных x∈X и y∈Y .
Отображения произведения множеств в его множители называют координатными функциями:
ϕ: X × Y → X, ϕ(x,y)=x и ψ: X × Y → X, ψ(x,y)=y.
Отображения произведения множеств в его множители называют координатными функциями:
ϕ: X × Y → X, ϕ(x,y)=x и ψ: X × Y → X, ψ(x,y)=y.
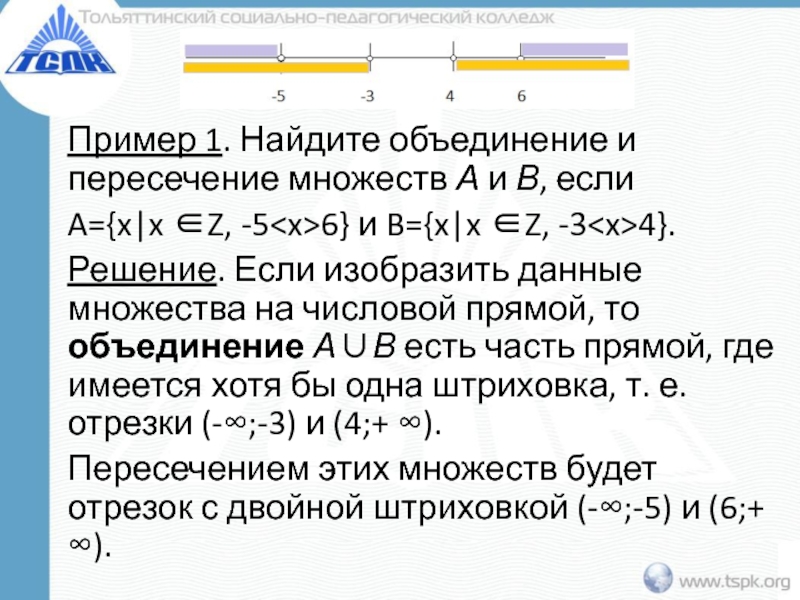
Слайд 13Пример 1. Найдите объединение и пересечение множеств А и В, если
A={x|x ∈Z, -56} и
B={x|x ∈Z, -34}.
Решение. Если изобразить данные множества на числовой прямой, то объединение А∪В есть часть прямой, где имеется хотя бы одна штриховка, т. е. отрезки (-∞;-3) и (4;+ ∞).
Пересечением этих множеств будет отрезок с двойной штриховкой (-∞;-5) и (6;+ ∞).
Решение. Если изобразить данные множества на числовой прямой, то объединение А∪В есть часть прямой, где имеется хотя бы одна штриховка, т. е. отрезки (-∞;-3) и (4;+ ∞).
Пересечением этих множеств будет отрезок с двойной штриховкой (-∞;-5) и (6;+ ∞).
Слайд 14Решение задач
Пример 2. В гимназии все ученики знают хотя бы один
из древних языков – греческий или латынь, некоторые – оба языка. 85% всех ребят знают греческий язык и 75% знают латынь. Какая часть учащихся знает оба языка?
Решение
100 – 85 = 15% всех ребят не знают греческий язык, то есть знают только латынь. Это значит, что 75 – 15 = 60% говорят на обоих языках.
Решение
100 – 85 = 15% всех ребят не знают греческий язык, то есть знают только латынь. Это значит, что 75 – 15 = 60% говорят на обоих языках.
Слайд 15Решение задач
Пример 3. Баба Яга в своей избушке на курьих ножках завела сказочных
животных. Все они, кроме двух, — Говорящие Коты; все, кроме двух, — Мудрые Совы; остальные — Усатые Тараканы. Сколько обитателей в избушке у Бабы Яги?
Подсказка: Подумайте, сколько в избушке Мудрых Сов и Усатых Тараканов вместе? А сколько Говорящих Котов и Усатых Тараканов вместе?
Подсказка: Подумайте, сколько в избушке Мудрых Сов и Усатых Тараканов вместе? А сколько Говорящих Котов и Усатых Тараканов вместе?
Слайд 16Решение задач
Решение. Из условия задачи следует, что Мудрых Сов и Усатых Тараканов — двое,
а Говорящих Котов и Усатых Тараканов — тоже двое. Это выполняется в двух случаях: либо Тараканов — 2, Котов и Сов — 0, либо и Котов, и Сов, и Тараканов — по одному. Первый случай не годится, так как в условии сказано, что и Совы, и Коты живут в избушке. Значит, у Бабы Яги поселились Говорящий Кот, Мудрая Сова и Усатый Таракан — всего трое.
Ответ: Трое, не считая Бабы Яги.
Ответ: Трое, не считая Бабы Яги.
Слайд 17Решение задач
Пример 4. В первом пенале лежат лиловая ручка, зелёный карандаш и красный
ластик; во втором — синяя ручка, зелёный карандаш и жёлтый ластик; в третьем — лиловая ручка, оранжевый карандаш и жёлтый ластик. Содержимое этих пеналов характеризуется такой закономерностью: в каждых двух из них ровно одна пара предметов совпадает и по цвету, и по назначению. Что должно лежать в четвёртом пенале, чтобы эта закономерность сохранилась?
Подсказка: Подумайте, может ли в четвёртом пенале лежать лиловая ручка.
Решение: В четвёртом пенале должны лежать предметы, которые уже встречаются в первых трех пеналах, но только по одному разу. Это синяя ручка, оранжевый карандаш и красный ластик.
Ответ
Синяя ручка, оранжевый карандаш, красный ластик.
Подсказка: Подумайте, может ли в четвёртом пенале лежать лиловая ручка.
Решение: В четвёртом пенале должны лежать предметы, которые уже встречаются в первых трех пеналах, но только по одному разу. Это синяя ручка, оранжевый карандаш и красный ластик.
Ответ
Синяя ручка, оранжевый карандаш, красный ластик.
Слайд 18Решение задач
Решение: В четвёртом пенале должны лежать предметы, которые уже встречаются в первых
трех пеналах, но только по одному разу. Это синяя ручка, оранжевый карандаш и красный ластик.
Ответ
Синяя ручка, оранжевый карандаш, красный ластик.
Ответ
Синяя ручка, оранжевый карандаш, красный ластик.
Слайд 19Самостоятельная работа:
Написать конспекты по темам:
Понятие разбиения множества на классы.
Число элементов
в объединении и разности конечных множеств.
Число элементов в декартовом произведении конечных множеств.
Составление кроссворда по теме «Множества и операции над ними»
Число элементов в декартовом произведении конечных множеств.
Составление кроссворда по теме «Множества и операции над ними»