- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Полиномы от одной переменной. Нохождение НОД. (Лекция 5.2) презентация
Содержание
- 1. Полиномы от одной переменной. Нохождение НОД. (Лекция 5.2)
- 2. «Наивный» метод т.е. Пример: Вычислить НОД полиномов
- 3. Пример: p5=НОД(f5,g5): w=х-3, v=х+2, НОД=1, но w5=v5=х+2 и, таким образом, НОД(w5,v5)=х+2.
- 4. Граница для коэффициентов НОД двух полиномов. Теорема (неравенство Ландау-Миньотта).
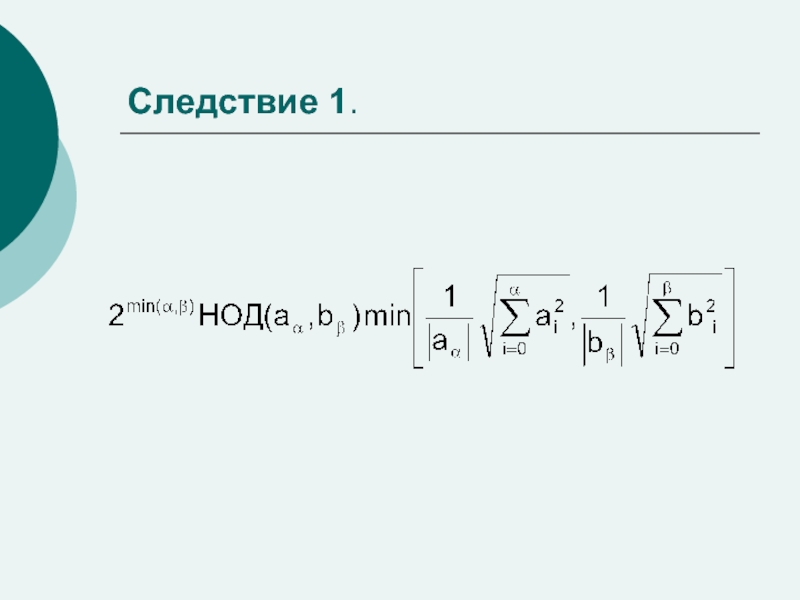
- 5. Следствие 1.
- 6. Лемма 1. Если число p не делит
- 7. Следствие. Если число р не делит старшие
- 8. Отсюда следует, что существует только конечное
- 9. Вычисление НОД М:= граница_Ландау_Миньотта (А,В); цикл до
- 10. алгоритм граница_Ландау_Миньотта применяет следствие их неравенства;
- 11. М:= граница_Ландау_Миньотта (А,В); Кроме:= НОД(lc(A), lc(B)); E0:
- 12. lc – старший коэффициент полинома; найти_простое
- 13. Оценка стоимости алгоритма . Время вычисления
«Наивный» метод т.е. Пример: Вычислить НОД полиномов
Слайд 6Лемма 1.
Если число p не делит старший коэффициент НОД(a,b) полиномов
a и b, то степень НОД(aр,bр) больше или равна степени НОД(f,g).
Слайд 7Следствие.
Если число р не делит старшие коэффициенты полиномов a и b
(в частности, может делить один из них, но не оба одновременно), то степень НОД (aр,bр) больше или равна степени НОД(a,b).
Слайд 8Отсюда следует, что существует только конечное число значений р,
таких, что степень НОД(ap,bp) отличается от степени НОД(а,b):
Лемма 2. Пусть с=НОД(а,b). Если число р удовлетворяет условию следствия и если р не делит Resx(a/c,b/c), то НОД(ap,bp)=cp.
это те р, которые делят НОД старших коэффициентов;
это те р, которые делят результант, упоминающийся в лемме (почему у него конечное число делителей !!??).
Слайд 9Вычисление НОД
М:= граница_Ландау_Миньотта (А,В);
цикл до бесконечности
Р:= найти_большое_простое (2М)
если степень_остатка (р,А) или степень_остатка (р,В)
то С:=модулярный_НОД (А,В,р);
если делит (С,А) и делит (С,В)
то выход С;
то С:=модулярный_НОД (А,В,р);
если делит (С,А) и делит (С,В)
то выход С;
Слайд 10алгоритм граница_Ландау_Миньотта применяет следствие их неравенства;
алгоритм найти_большое_простое возвращает простое число, большее
чем его аргумент (каждый раз новое число);
алгоритм степень_остатка проверяет, что редукция по модулю р не меняет степень, т.е. р не делит старший коэффициент;
алгоритм модулярный_НОД применяет алгоритм Евклида по модулю р;
алгоритм делит проверяет, что многочлены делятся над кольцом целых чисел
алгоритм степень_остатка проверяет, что редукция по модулю р не меняет степень, т.е. р не делит старший коэффициент;
алгоритм модулярный_НОД применяет алгоритм Евклида по модулю р;
алгоритм делит проверяет, что многочлены делятся над кольцом целых чисел
Слайд 11М:= граница_Ландау_Миньотта (А,В);
Кроме:= НОД(lc(A), lc(B));
E0: р:=найти_простое (Кроме);
С:= модулярный_НОД (А,В,р);
E1:
если степень (С)=0 то выход 1;
Дано:=р;
Результат:=С;
Цикл пока Дано ≤ 2М
р:=найти_простое (Кроме);
С:= модулярный_НОД (А,В,р);
если степень (С)< степень (Результат) то идти на Е1;
если степень (С)= степень (Результат)
то Результат:=CRT(Результат, Дано, С, р);
Дано:= Дано·р;
если делит (Результат, А) и делит (Результат, В)
то выход Результат;
идти на ЕО;
Дано:=р;
Результат:=С;
Цикл пока Дано ≤ 2М
р:=найти_простое (Кроме);
С:= модулярный_НОД (А,В,р);
если степень (С)< степень (Результат) то идти на Е1;
если степень (С)= степень (Результат)
то Результат:=CRT(Результат, Дано, С, р);
Дано:= Дано·р;
если делит (Результат, А) и делит (Результат, В)
то выход Результат;
идти на ЕО;
Слайд 12lc – старший коэффициент полинома;
найти_простое – выдает простое число, не делящее
его аргумент (каждый раз новое число);
CRT – применяет китайскую теорему об остатках к каждому коэффициенту двух полиномов – Результат (по модулю Дано) и С (по модулю р), представляя целые числа по модулю М между –М/2 и М
CRT – применяет китайскую теорему об остатках к каждому коэффициенту двух полиномов – Результат (по модулю Дано) и С (по модулю р), представляя целые числа по модулю М между –М/2 и М
Слайд 13Оценка стоимости алгоритма
.
Время вычисления ограничивается величиной О(n3·log23·H), где n - такое,
что степени полиномов a, b не больше этого числа;
H - величина, удовлетворяющая неравенству
H - величина, удовлетворяющая неравенству
