- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка к ЕГЭ. Решение задач группы С2. Стереометрия презентация
Содержание
- 1. Подготовка к ЕГЭ. Решение задач группы С2. Стереометрия
- 2. D А В С А1
- 3. В кубе ABCDA1B1C1D1
- 4. В кубе ABCDA1B1C1D1 все
- 5. В кубе
- 6.
- 7. Решение. В правильном тетраэдре ABCD
- 8. В правильном тетраэдре ABCD точка E –середина
- 9. Реши самостоятельно 1. В правильной четырехугольной
- 10. 1. В
- 11. A B C D E
Слайд 2
D
А
В
С
А1
D1
С1
В1
1
1
1
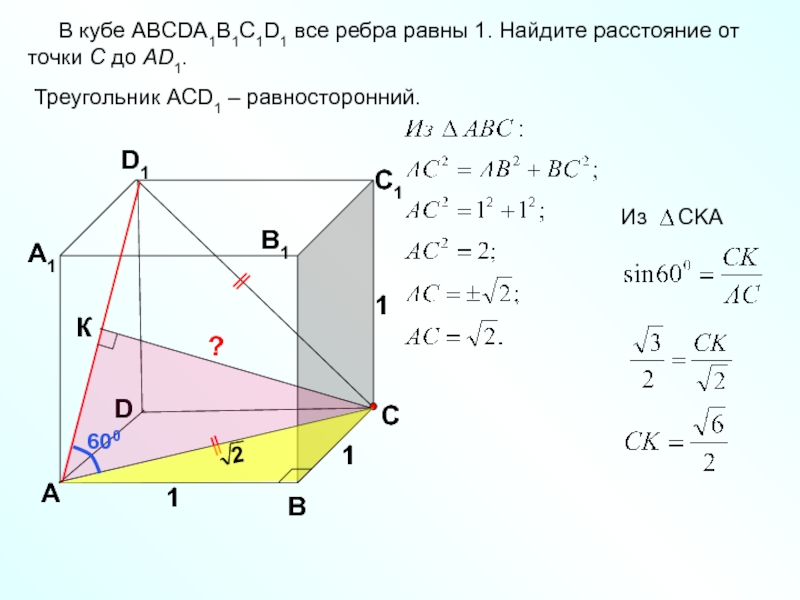
Треугольник ACD1 – равносторонний.
В кубе ABCDA1B1C1D1 все
?
Слайд 3
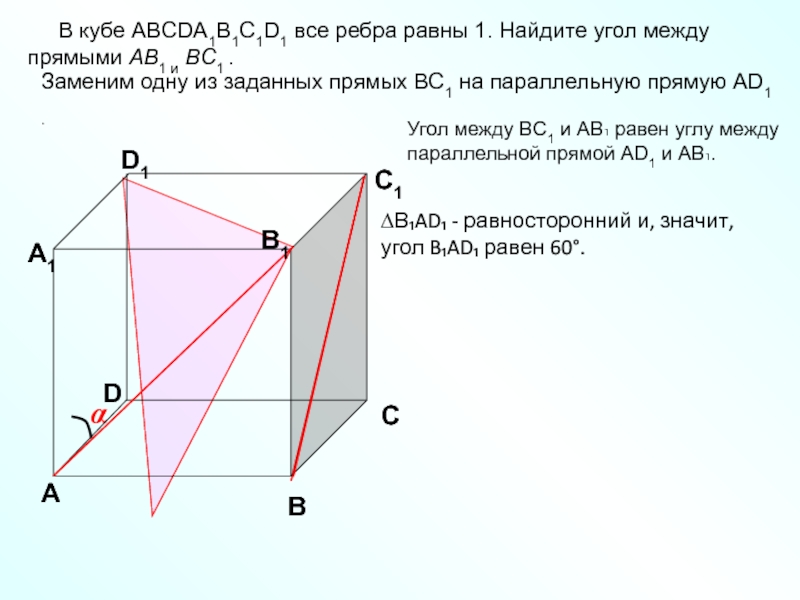
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите
Заменим одну из заданных прямых BC1 на параллельную прямую AD1 .
∆B₁AD₁ - равносторонний и, значит, угол B₁AD₁ равен 60°.
Угол между BC1 и АB₁ равен углу между параллельной прямой AD1 и АB₁.
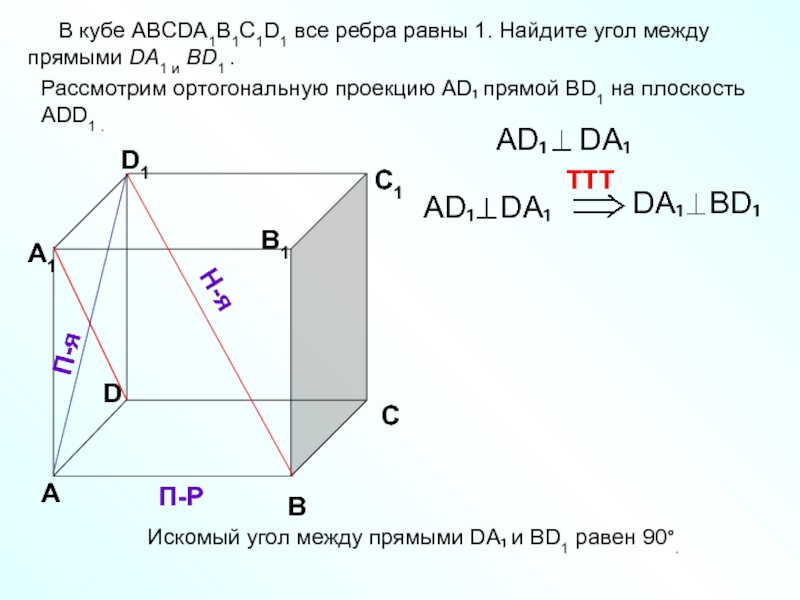
Слайд 4 В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите
Рассмотрим ортогональную проекцию AD₁ прямой BD1 на плоскость ADD1 .
П-Р
Н-я
П-я
Искомый угол между прямыми DA₁ и BD1 равен 90°.
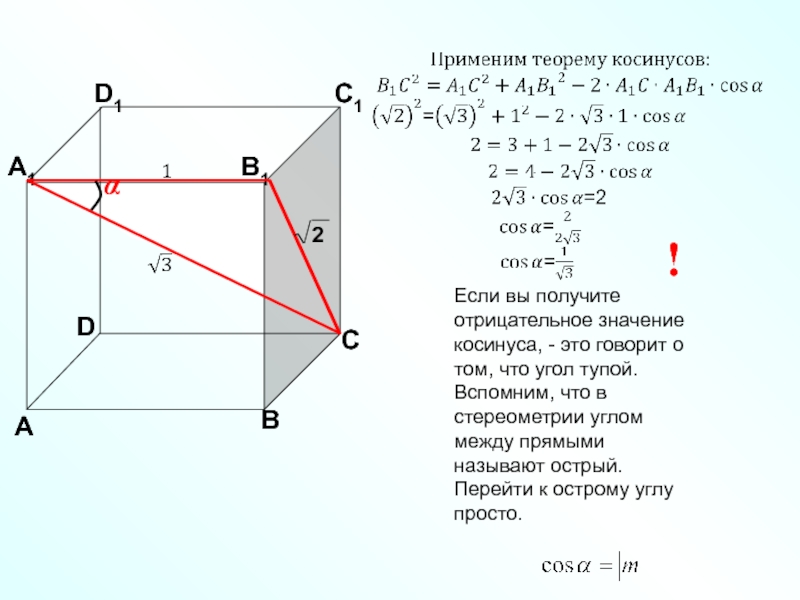
Слайд 5
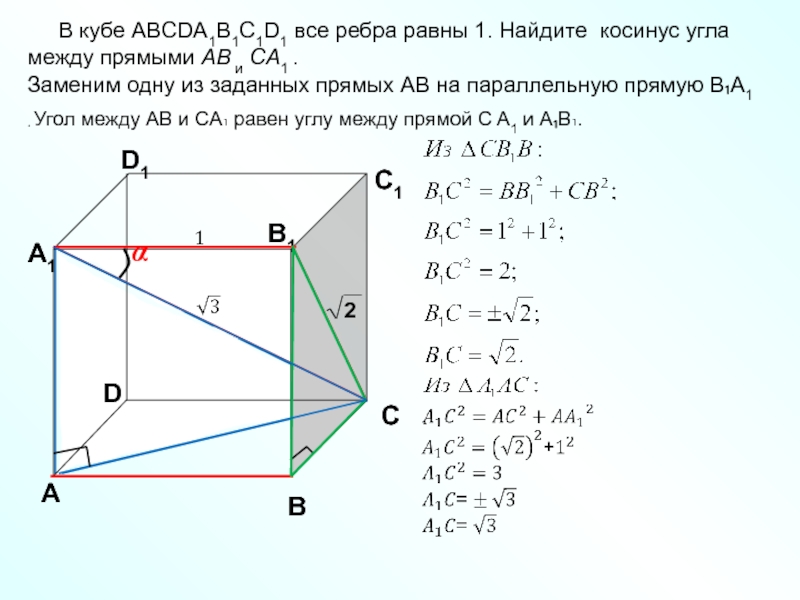
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите
Заменим одну из заданных прямых AB на параллельную прямую B₁A1 .
Угол между AB и CА₁ равен углу между прямой C A1 и А₁B₁.
Слайд 7
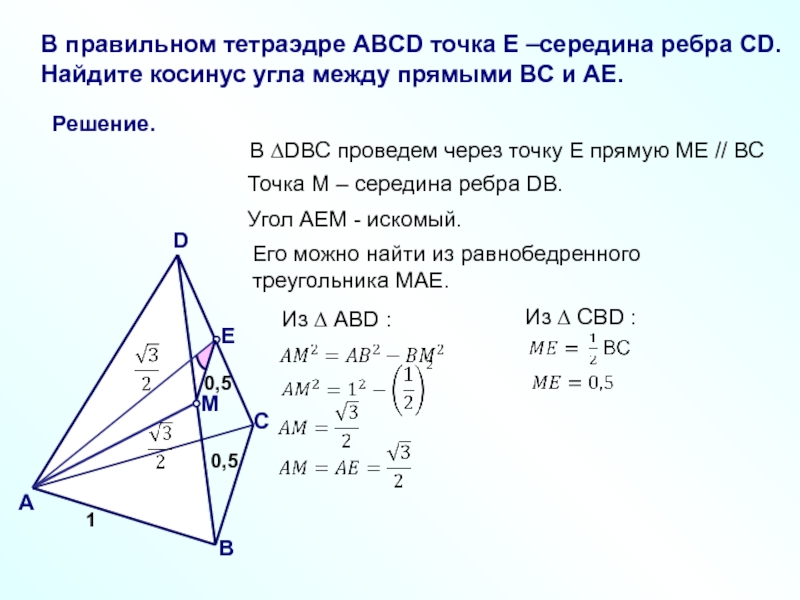
Решение.
В правильном тетраэдре ABCD точка E –середина ребра CD. Найдите косинус
M
В ∆DBC проведем через точку E прямую ME // BC
Точка М – середина ребра DB.
Угол AEM - искомый.
Его можно найти из равнобедренного треугольника MAE.
Из ∆ АВD :
1
0,5
Из ∆ СВD :
0,5
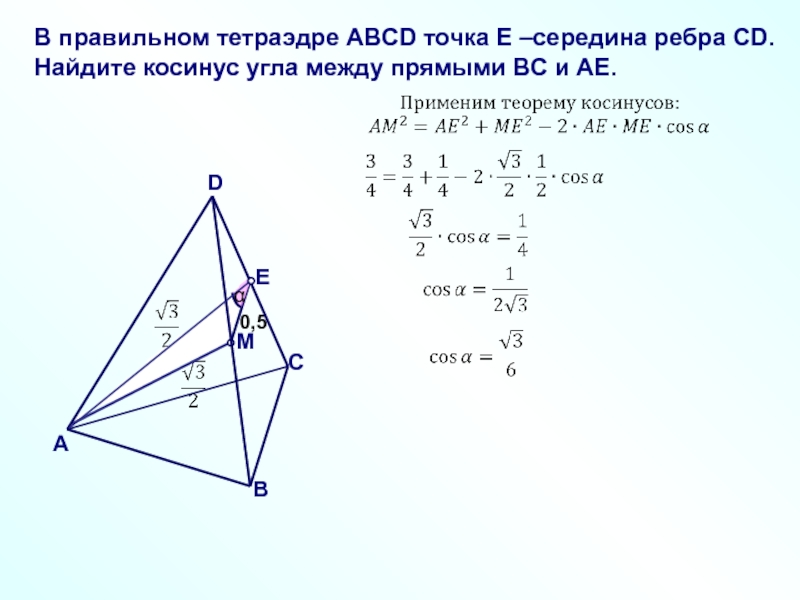
Слайд 8В правильном тетраэдре ABCD точка E –середина ребра CD. Найдите косинус
Слайд 9Реши самостоятельно
1. В правильной четырехугольной пирамиде SABCD, все ребра которой
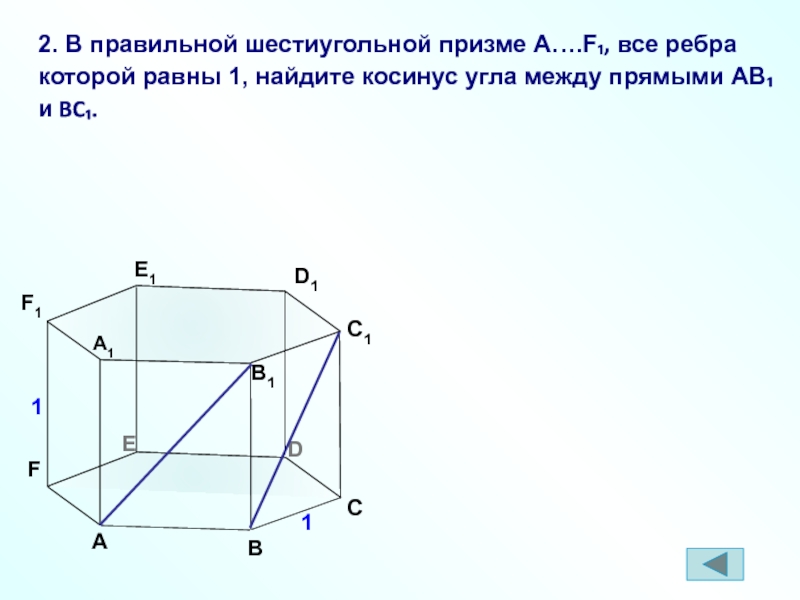
2. В правильной шестиугольной призме A….F₁, все ребра которой равны 1, найдите косинус угла между прямыми AB₁ и BC₁.
Чертеж и подсказка
Чертеж и подсказка
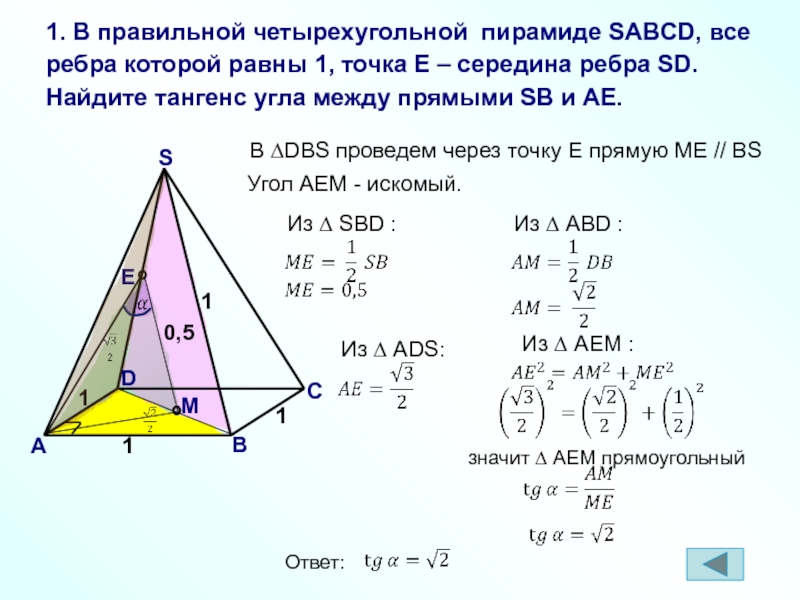
Слайд 10
1. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1,
E
В ∆DBS проведем через точку E прямую ME // BS
M
Угол AEM - искомый.
Из ∆ SВD :
1
1
0,5
1
1
Из ∆ AВD :
Из ∆ AEM :
Из ∆ ADS:
значит ∆ AEM прямоугольный
Ответ:
Слайд 11
A
B
C
D
E
B1
C1
D1
E1
1
1
A1
F
F1
2. В правильной шестиугольной призме A….F₁, все ребра которой равны 1,
